Journal of Signal and Information Processing
Vol.05 No.04(2014), Article ID:51523,6 pages
10.4236/jsip.2014.54020
Tree Matrix Algorithm of LDPC Codes
Huanming Zhang
Electronics and Information Engineering Institute, Foshan University, Foshan, China
Email: huanmingzhang@126.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 September 2014; revised 15 October 2014; accepted 8 November 2014
ABSTRACT
LDPC codes are finding increasing use in applications requiring reliable and highly efficient information transfer over bandwidth. An LDPC code is defined by a sparse parity-check matrix and can be described by a bipartite graph called Tanner graph. Loops in Tanner graph prevent the sum-product algorithm from converging. Further, loops, especially short loops, degrade the performance of LDPC decoder, because they affect the independence of the extrinsic information exchanged in the iterative decoding. This paper, by graph theory, deduces cut-node tree graph of LDPC code, and depicts it with matrix. On the basis of tree matrix algorithm, whole depictions of loops can be figured out, providing of foundation for further research of relations between loops and LDPC codes’ performance.
Keywords:
LDPC, Belief Propagation (BP), Graph, Iterative Decoding, Loop, Cycle

1. Introduction
Probability distributions defined by graphs are used in literature of various fields, such as coding theory, artificial intelligence, and system theory.
LDPC [1] code can be depicted by its parity-check matrix H [2] , 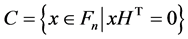 and its degree distribution of polynomial [3] :
and its degree distribution of polynomial [3] :
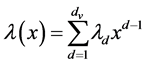 (1)
(1)
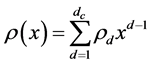 (2)
(2)
Computing distributions of variable and check nodes in a Tanner graph is relatively efficient without cycle, but complex with cycles, even difficult when cycles are short for large graph.
The belief propagation algorithm [4] , or known as the sum-product algorithm [5] is decoding algorithm for graphical codes, such as convolution code, turbo code and LDPC code.
Belief propagation (BP) algorithm is optimal and produces exact solutions on a tree just in a finite number of iterations. Otherwise, BP algorithm may not converge. Moreover, when it doses converge, it provides approximate solution and the results vary in different conditions.
2. Background
In most common sense of the term, an undirected graph [6] consists of a set of vertices or nodes V together with a set of edges E, which are 2-element subsets of V (i.e., an edge is related with two vertices, and the relation is represented as an unordered pair of the vertices with respect to the particular edge). See Figure 1.
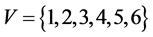
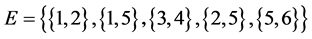
n = 6
m = 5
Let 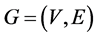 be an undirected graph.
be an undirected graph.
The following statements are equivalent,
1. G is a tree
2. Any two vertices in G are connected by a unique simple path
3. G is connected, but if any edge is removed from E, the resulting graph is disconnected
4. G is connected, and 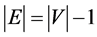
5. G is acyclic, and 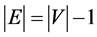
6. G is acyclic, but if any edge is added to E, the resulting graph contains a loop.
In fact, a tree is a connected graph without any cycles; a leaf is a vertex of degree 1. An internal vertex is a vertex of degree at least 2.
In coding theory, Tanner graph, named after Michael Tanner, is a bipartite graph used to state constraints or equations which specify error correcting codes. See Figure 2. They are used to construct longer codes from smaller ones. Both encoders and decoders employ these graphs extensively.
Figure 1. An example of a graph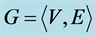 .
.
Figure 2. Tanner graph of an LDPC code (a cycle represented by 4 bold lines in figure).
In communication system, the transmitted random vector 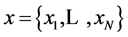 is not observed; instead received noisy vector
is not observed; instead received noisy vector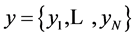 .
.
N is the length of codeword, Parity check equation vector is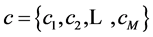 , M is the number of equations.
, M is the number of equations. 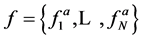 represents initial information about transmitted codeword.
represents initial information about transmitted codeword.
where, 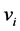 is the ith variable node,
is the ith variable node, 
The belief propagation (BP) of LDPC code states as follows [7] - [11] :










where 

Figure 3. Iterative decoding algorithm.
Figure 4. Updating rule for message passing.
3. Principle of Cut-Node Tree
In order to solute loops of LDPC code, Tanner graph is re-drew as following principle: Choosing an element “1” in H, its variable (or check) node considered root node, check (or variable) nodes connected to the variable (or check) node as 1st order child-nodes, a current node, once appearance in ancestor node or sibling node, will be cut and forbid to grow and become a end node like a leaf, but not a leaf actually. And so forth, at last a cut-node tree can be get. If all nodes are connected, a single cut-node tree can be get, otherwise it is forest. Repeating this process until all end nodes are either cut-node or leaf node. See Figure 5.
HH is mark matrix, every element in HH is zero represents end of algorithm.
Figure 5. Flow process chart of algorithm.
4. Implement of Principle and Results
First, a node (variable node or check node), for instance, variable node
An example: for

has following cut-node tree graph (Figure 6).
Another example: For instance, an LDPC code with check matrix H:

Following tree matrix expressed by matlab can be get:

In fact, tree matrix matches along with Tree of Graph, [i j k l m], [i j] states current node, [k l] states father node, m states times being cut.
So, searched by a computer, all loops can be get:
Figure 6. Tree graph of LDPC codes.
Loop 1: [4 8]-[3 8]-[3 5]-[2 5]-[2 6]-[4 6]-[4 8]
Loop 2: [5 9]-[3 9]-[3 5]-[2 5]-[2 7]-[5 7]-[5 10]
Loop 3: [5 10]-[4 10]-[4 6]-[2 6]-[2 7]-[5 7]-[5 10]
Loop 4: [1 1]-[1 2]-[3 2]-[3 5]-[2 5]-[2 1]-[1 1]
Loop 5: [1 3]-[1 2]-[3 2]-[3 5]-[2 5]-[2 6]-[4 6]-[4 3]-[1 3]
Loop 6: [1 4]-[1 2]-[3 2]-[3 5]-[2 5]-[2 7]-[5 7]-[5 4]-[1 4]
Loop 7: [1 1]-[1 3]-[4 3]-[4 6]-[2 6]-[2 1]-[1 1]
Loop 8: [1 1]-[1 3]-[4 3]-[4 6]-[2 6]-[2 5]-[3 5]-[3 2]-[1 2]-[1 1]
Loop 9: [1 4]-[1 3]-[4 3]-[4 6]-[2 6]-[2 5]-[3 5]-[3 2]-[1 2]-[1 4]
Loop 10: [1 4]-[1 3]-[4 3]-[4 6]-[2 6]-[2 7]-[5 7]-[5 4]-[1 4]
Loop 11: [1 1]-[1 4]-[5 4]-[5 7]-[2 7]-[2 1]-[1 1]
Loop 12: [1 1]-[1 4]-[5 4]-[5 7]-[2 7]-[2 5]-[3 5]-[3 2]-[1 2]-[1 1]
Loop 13: [1 1]-[1 4]-[5 4]-[5 7]-[2 7]-[2 6]-[4 6]-[4 3]-[1 3]-[1 1]
Loop 14: [1 2]-[1 4]-[5 4]-[5 7]-[2 7]-[2 5]-[3 5]-[3 2]-[1 2]
Loop 15: [1 2]-[1 4]-[5 4]-[5 7]-[2 7]-[2 6]-[4 6]-[4 3]-[1 3]-[1 2]
Loop 16: [1 3]-[1 4]-[5 4]-[5 7]-[2 7]-[2 5]-[3 5]-[3 2]-[1 2]-[1 3]
Here, H is just a situation of single tree, with 15 cut-nodes, no leaf node and 16 loops. See Table 1. Further, Message-passing form for cut-node tree has following rule:
In a tree, Message-passing fellows a two-pass form, first sweeping upwards from leaves to a node designated as the root, and then downwards from the root to leaves.
In a graph with cycle, Cut-node tree graph can be get by cutting all loops, See Figure 7.
Cut node tree has all same characters with Tanner graph.
Figure 7. Message passing over cut-node tree graph.
Table 1. Features of loops about above example.
5. Conclusion
This paper provides a new method to describe graph of LDPC codes, it aims to solute loops of LDPC codes and message passing over cut node tree. For a large matrix H, it is difficult to solute loops, because loops convolve each other. Features of loops have certain relationship with performances. In this paper, a cut node tree can be expressed by a certain matrix. By computer simulation, cut-node tree can get right answer and give out method to calculate loops of LDPC codes and cut node tree graph, its results assist to further research this relationship.
References
- Gallager, R.G. (1963) Low-Density Parity Check Codes. MIT Press, Cambridge.
- Mackay, D.J.C. (1999) Good Error-Correcting Codes Based on Very Sparse Matrices. IEEE Transactions on Information Theory, 45, 399-431. http://dx.doi.org/10.1109/18.748992
- Tanner, R.M. (1981) A Recursive Approach to Low Complexity Codes. IEEE Transactions on Information Theory, 27, 533-547. http://dx.doi.org/10.1109/TIT.1981.1056404
- Kschischang, R., Frey, B.J. and Loeliger, H.A. (2001) Factor Graphs and the Sum-Product Algorithm. IEEE Transactions on Information Theory, 47, 498-519. http://dx.doi.org/10.1109/18.910572
- Wiberg, N. (1996) Codes and Decoding on General Graphs, Linkoping Studies in Science and Technology. Ph.D. Dissertation, No. 440, Linköping University, Linköping.
- Reinhard, D. (1997) Graph Theory. Springer-Verlag, New York.
- Wainwright, M.J. (2007) Sparse Graph Codes for Side Information and Binning. IEEE Signal Processing Magazine, 47, 47-57.
- Forney Jr., G.D. (2001) Codes on Graphs: Normal Realizations. IEEE Transactions on Information Theory, 47, 520- 548. http://dx.doi.org/10.1109/18.910573
- Loeliger, H.A. (2004) An Introduction to Factor Graph. IEEE Signal Processing Magazine, 28-41.
- Kschischang, F.R. (2003) Codes Defined on Graphs. IEEE Communications Magazine, 118-125.
- Vontobel, P.O. (2004) A Factor-Graph Approach to the Context-Tree Weighting Method. Proceedings of the Data Compression Conference (DCC’04), 571.
- Wainwright, M., Jaakkola, T. and Willsky, A. (2002) Tree-Based Reparameterization Analysis of Belief Propagation and Related Algorithms for Approximate Inference on Graphs with Cycles. ISIT2002, Lausanne, 30 June-5 July 2002.









