Journal of Signal and Information Processing
Vol. 3 No. 3 (2012) , Article ID: 22128 , 8 pages DOI:10.4236/jsip.2012.33045
Performance Evaluation of Complex Wavelet Packet Modulation (CWPM) System over Multipath Rayleigh Fading Channel
![]()
Electrical Engineering Department, Al-Mustansiryah University, Baghdad, Iraq.
Email: hikmat_04@yahoo.com, fadel_sahib@yahoo.com
Received April 5th, 2012; revised May 1st, 2012; accepted May 15th, 2012
Keywords: Multicarrier Modulation; Wavelet Packet Modulation; Complex Wavelet Transform
ABSTRACT
In this paper a novel multicarrier modulation system called Complex Wavelet Packet Modulation (CWPM) has been proposed. It is based on using the Complex Wavelet Transform (CWT) together with the Wavelet Packet Modulation (WPM). The proposed system has been tested for communication over flat and frequency selective Rayleigh fading channels and its performance has been compared with some other multicarrier systems. The simulation results show that the performance of the proposed CWPM system has the best performance in all types of channel considered as compared with OFDM, Slantlet based OFDM, FRAT based OFDM and WPM systems. Furthermore, the proposed scheme has less PAPR as compared with the traditional WPM multicarrier system.
1. Introduction
Multicarrier modulation (MCM) [1] based on the discrete Fourier transform (DFT) has been adopted as the modulation/demodulation scheme of choice in several digital communications standards. These include wire line systems such as digital subscriber lines (DSL), wireless systems such as digital audio and terrestrial video broadcast (DAB/DVB-T), local area networks such as IEEE 802.11a/g/n, and metropolitan area networks such as IEEE802.16a, where it is commonly known as orthogonal frequency-division multiplexing (OFDM).
In recent years different types of multicarrier modulation are produced like slantlet based OFDM [2], FRAT based OFDM [3,4] and wavelet based OFDM [5-8]. Wavelet packet Modulation (WPM) [9] is a carrierless that uses a filtering and defiltering technique to convey orthogonal multi-sub-band information from transmitter to receiver. WPM shares all the benefits of multicarrier technique and exhibits further benefit such as higher efficiency due to elimination of guard interval (GI). It is considered as one of wavelet transforms which are well localized both in time and frequency domain, while sinusoid waveforms are only localized in frequency but not in time domain. The wavelet and subband transform applications in communications are viewed in [9]. Besides the features mentioned previously, WPM has additional attractive features inherited from the wavelet packet modulation: the Wavelet Transform (WT) is widely adopted in image/video and speech coding. Its use for modulation/demodulation on frequency-selective channels results in a better integrated system design and a reduced overall implementation cost. The WPT uses only real arithmetic, as opposed to the complex-valued DFT. This reduces the signal-processing complexity/power consumption, but it suffers from three major limitations: shift sensitivity, poor directionality, and absence of phase information. To solve these problems, Complex wavelet transform (CWT) [10] are proposed and applied in many signal processing applications especially in image processing applications [11-13].
In this paper, the principles of CWT are applied to WPM in order to improve its performance introducing a novel multicarrier communication scheme called complex wavelet packet modulation (CWPM). The rest of the paper is arranged as follows: the next section reviews the discrete wavelet packet transform. Section 3 presents the proposed complex wavelet packet modulation system. Section 4 shows the simulation results while the conclusions deduced through the work are given in Section 5.
2. Discrete Wavelet Packet Transform (DWPT)
Wavelet packets are a class of generalized Fourier transforms with basis functions localizing well in both time and frequency domains. They are constructed using Quadrature Mirror Filter (QMF) pairs h(n) and g(n), satisfying the following conditions [14]:
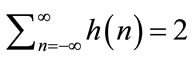 (1)
(1)
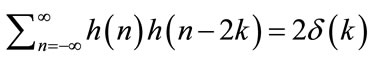 (2)
(2)
 (3)
(3)
where usually h(n) and g(n) are low-pass and high-pass filters, respectively, and L is the span of the filters. The QMFs h(n) and g(n) are recursively used to define the sequence of basis functions φn(t), called wavelet packets as follows:
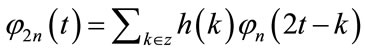 (4)
(4)
 (5)
(5)
Wavelet packets have the following orthogonality properties:
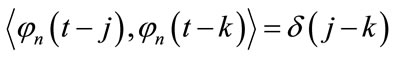 (6)
(6)
 (7)
(7)
where  is the inner product of functions and δ(.) is the delta function. Based on h(n) and g(n), and the corresponding reversed filters h(−n) and g(−n), four operators (H−1, G−1, H and G) are defined that can be used to construct a wavelet packet tree. H and G are the downsampling convolution operators and H−1 and G−1 are upsampling deconvolution operators. The four operators acting on the sequence of samples x(n) are defined as follows [12]:
is the inner product of functions and δ(.) is the delta function. Based on h(n) and g(n), and the corresponding reversed filters h(−n) and g(−n), four operators (H−1, G−1, H and G) are defined that can be used to construct a wavelet packet tree. H and G are the downsampling convolution operators and H−1 and G−1 are upsampling deconvolution operators. The four operators acting on the sequence of samples x(n) are defined as follows [12]:
 (8)
(8)
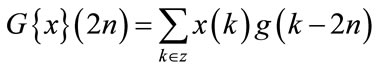 (9)
(9)
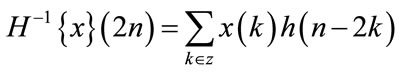 (10)
(10)
 (11)
(11)
Figure 1 shows the construction of these operators. The operators H and G can be used to decompose (analyze) any discrete function x(n) on the space l2(z) into two orthogonal subspaces l2(z). Each decomposition (H or G) step results in two coefficient vectors each half the length of the input vector keeping the total length of data unchanged. This operation can be iterated by cascading the operators for multiple numbers of steps. In this iterative decomposition procedure, the output coefficient vectors have size reduced at each step by 2 so that eventually these output vectors become scalars. This decomposition process using G and H is called Discrete Wavelet Packet Transform (DWPT). The decomposition is a reversible process and the Inverse Discrete Wavelet Packet Transform (IDWPT) can be used to reconstruct the original input vector from the coefficients vectors. The IDWPT is a series of upsampling filtering processes defined by the operators H−1 and G−1. Figure 2 shows a full DWPT tree (on the left side) and a full IDWPT tree (on the right side) which are used in the WPM system for demodulation and modulation, respectively.
3. Complex Wavelet Packet Modulation (CWPM)
Figure 3 illustrates the block diagram of proposed CWPM transceiver. CWPM system employs two filter banks performs Inverse Discrete Wavelet Packet Transform (IDWPT) placed at transmitter side, and Discrete Wavelet Packet Transform (DWPT) placed at the receiver side. The block “MAKE CMPLX” accepts two N-dimensional real vectors as inputs. Its output is an N-dimensional complex vector whose ith complex element is formed from the ith real elements of the two input vectors. The
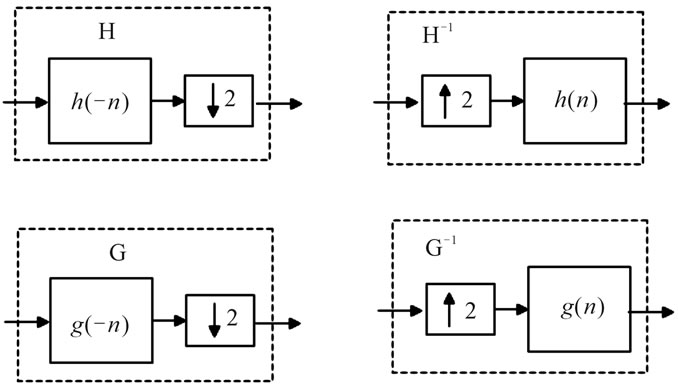
Figure 1. Example of a figure caption analysis and synthesis filters using H, G, H−1, G−1 operators.

Figure 2. Wavelet packet trees: analysis/DWPT (demodulation) and synthesis/IDWPT (modulation).
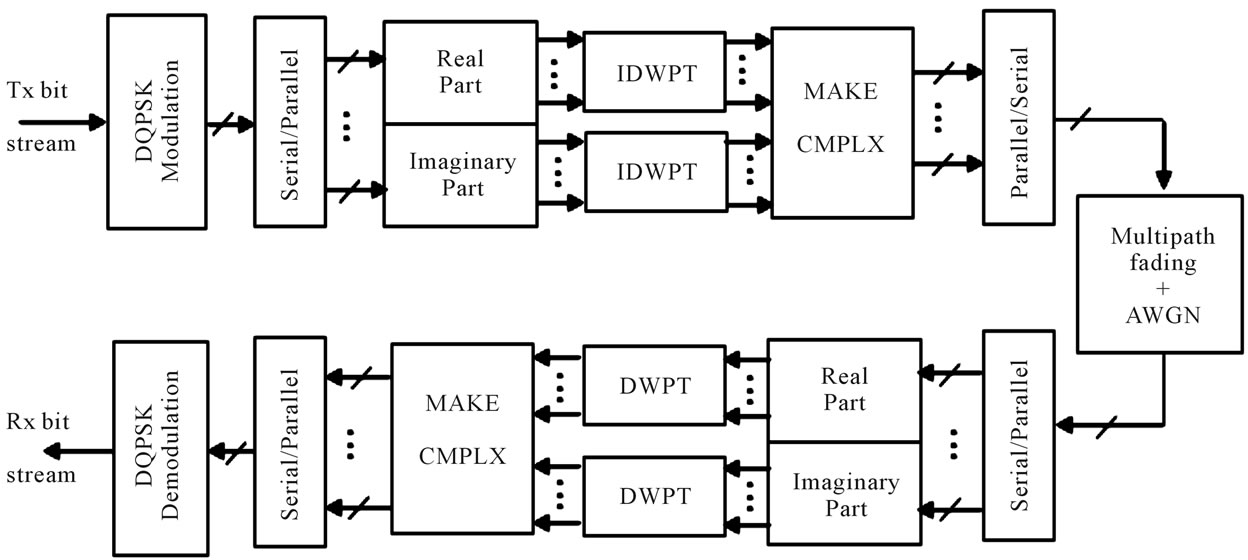
Figure 3. Block diagram of CWPM system (arrows with astrike indicate complex quantities).
input to the inverse wavelet transform is DQPSK complex symbols, therefore, there are two IDWPT blocks, one for real symbols and the other for imaginary symbols. The outputs of two IDWPT are combined together in complex form to introduce the transmitted signal x[n]. The transmitted signal is constructed as the sum of N waveforms φj[k] individually modulated with the DQPSK symbols as follows:
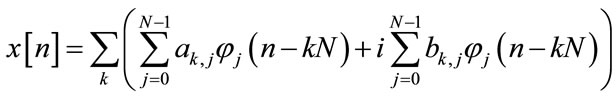 (12)
(12)
where ak,j, bk,j are the real and the imaginary constellations of the encoded kth data symbol modulating the jth wavelet packet basis function respectively. The IDWPT synthesizes a discrete representation of the transmitted signal as the sum of N waveforms shifted in time that embed information about the data symbols. The DWPT at the receiver recovers the transmitted symbols ak,j, bk,j through the analysis formula exploiting orthogonality properties of DWPT and is schematically represented in the right side of Figure 2.
4. Simulation Results
The performance results of the proposed CWPM system are obtained using MATLAB. These results are compared WPM, traditional OFDM (FFT based OFDM), Slantlet based OFDM and FRAT-OFDM systems over different channel models: the AWGN channel, the flat Rayleigh fading channel, and the frequency selective Rayleigh fading channel. OFDM is cyclically extended with guard sample 0.25 N and the number of carriers is taken to be 128. The type of wavelet family used was db6. For fading channels, two paths for the signal are considered. The second path delay was 8 Ts with a corresponding gain of −8 dB, where Ts is the sampling time. The Doppler spread factor (fdTs) is changed during the simulations to take one of the following values: 0.0025, 0.0075 and 0.015.
Figure 4 shows the performance of the proposed CWPM system in AWGN channel as compared with other systems mentioned above. It’s clearly shown that the proposed CWPM system has almost the same performance of WPM system but better than OFDM systems. For instant at BER = 10−3, CWPM has about 2 dB gain in SNR over FRAT-OFDM system while it has about 11 dB gain over OFDM and SLT-OFDM systems.
Figures 5-7 show the performance of proposed CWPM system as compared with other types of multicarrier modulation considered over flat Rayleigh fading channel for Doppler spread factors fdTs = 0.0025, 0.0075, and 0.015 respectively. From these figures, it can be seen
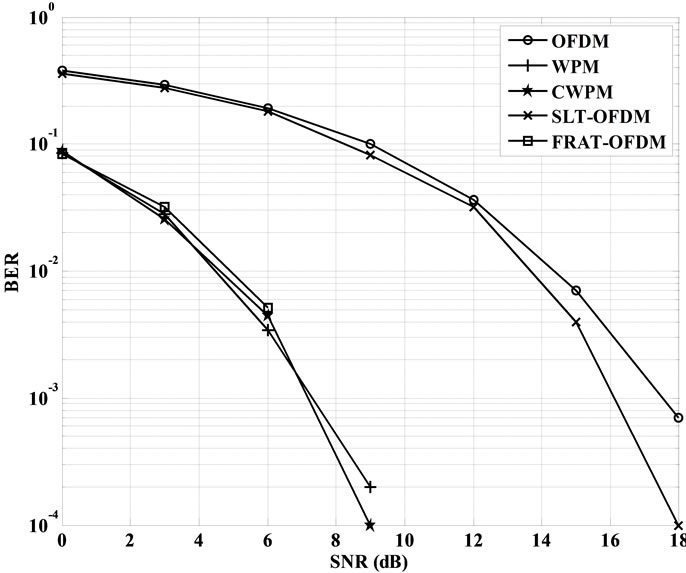
Figure 4. BER performance of CWPM in AWGN channel.

Figure 5. BER performance of CWPM in flat fading channel, fdTs = 0.0025.

Figure 6. BER performance of CWPM in flat fading channel, fdTs = 0.0075.

Figure 7. BER performance of CWPM in flat fading channel, fdTs = 0.015.
that the proposed system, together with WPM, is robust against flat fading channel for different Doppler spread factors while the performance of other systems like FRAT-OFDM is deteriorated as the Doppler spread factor increases.
Figures 8-10 show the performance of proposed CWPM system as compared with other types of multicarrier modulation considered over selective Rayleigh fading channel for Doppler spread factors fdTs = 0.0025, 0.0075, and 0.015 respectively. Once again the performance of the proposed system is superior than other ones including WPM different Doppler spread factors. For example, at BER = 10−3 CWPM has about 3 dB gain in SNR over WPM system when fdTs = 0.015 while other OFDM systems fail to achieve such a BER value at moderate SNR values.
4.1. The Effect of Wavelet Family
Three wavelet packets from three different families are used for this simulation namely Daubechies wavelet packets with order 6, db6, Symmlets wavelet packets with order 6 (sym6), and Coiflets wavelet packets with order 2, (coif2). These families are chosen because they are orthogonal and have compact support (i.e., fast decaying time, which results in good localization in both time and frequency). The filter length is taken to be L = 12. Figure 11 shows BER versus SNR for these three wavelet families for CWPM system for N = 128 over selective Rayleigh fading channel with Doppler spread factor fdTs = 0.015. From this figure, it’s shown that Daubechies family gives the best BER performance.
4.2. The Effect of Filter Length
Figure 12 shows the BER performance of CWPM over selective fading channel with fdTs = 0.015 for three wavelet packets from Daubechies family, namely Haar, db3, db6, db9 and db12 which have filter lengths, L = 2, 6, 12, 18 and 24 respectively. From this figure, it is shown that the increase of the filter length would enhance the BER performance. However, it is worth noted that as the filter length increases the data rate would be decreased. So, the selection of filter length should take in to account the necessary optimization process.
4.3. The Effect of Subcarrier Number
Figure 13 shows the BER performance of CWPM over selective fading channel with fdTs = 0.015 for various number of subcarriers (N = 64, 128, 256, and 512). The type of wavelet family is db6. From this figure, it is shown that as the number of subcarrier N increases, the enhancement of BER performance is decreased.
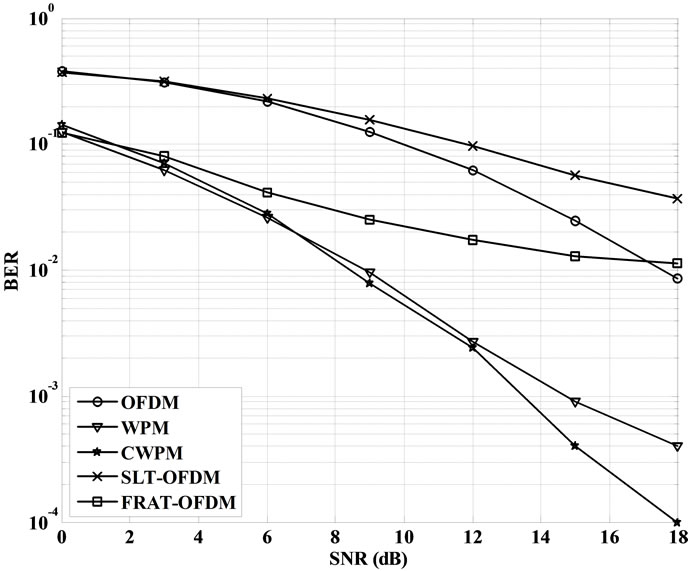
Figure 8. BER performance of CWPM in selective fading channel, fdTs = 0.0025.

Figure 9. BER performance of CWPM in selective fading channel, fdTs = 0.0075.

Figure 10. BER performance of CWPM in selective fading channel, fdTs = 0.015.

Figure 11. Effect of wavelet family on the BER performance.

Figure 12. Effect of filter length on the BER performance.

Figure 13. Effect of filter length on the BER performance.
4.4. PAPR Results
Figure 14 shows CCDF of the PAPR in the proposed CWPM system as compared with WPM and OFDM systems for N = 128 and Haar wavelet family. It’s seen that from this figure that the PAPR of CWPM is greater than OFDM by about 3 dB when CCDF = 0.1, but smaller than WPM by about 2 dB at the same CCDF value. Figures 15 and 16 show the CCDF of the PAPR of the proposed CWPM system after applying several wavelet families have the same filter length, L = 12 and various filter lengths of the Daubechies wavelet family respectively. All the configurations are taken to have 128 carriers. From these figures, one can easily see that Daubechies has the least PAPR as compared with other families and that the increase the filter length will increase PAPR of CWPM system. Finally, Figure 17 shows the CCDF of the PAPR of CWPM system for different number of subcarriers. From this figure, it is shown than the increase of subcarrier numbers will increase the PAPR of the system.
5. Conclusions
In this paper the complex wavelet packet modulation is designed and its performance is investigated by comparing it with some other multicarrier modulation systems over different channel types. The simulations show that CWPM is an efficient multicarrier scheme when working in flat and frequency selective Rayleigh fading channels. In AWGN channel, CWPM has almost the same performance of WPM scheme. The Change of wavelet family type and filter length and the number of subcarriers used in CWPM will effect on its BER performance. Daubechies family gives the best performance and as the filter length increases the performance is improved. The effect of changing the subcarriers is as this number is increased the performance of CWPM tends to be degraded. CCDF has been used as a measure of PAPR effect in CWPM as the case in other MC systems. It has been

Figure 14. CCDF of the PAPR of CWPM and other MC systems.

Figure 15. CCDF of PAPR for the CWPM and other MC systems, filter length L = 12.

Figure 16. CCDF of PAPR for the CWPM and other MC systems for different filter lengths of Daubechies family.

Figure 17. CCDF of PAPR for the CWPM and other MC systems for different number of subcarriers.
shown that the PAPR of CWPM is greater than OFDM and but less than WPM system. The type of wavelet family and filter length has also impact on PAPR. Daubechies gives the least PAPR among families considered in the study.
REFERENCES
- J. Bingham, “Multicarrier Modulation for Data Transmission: An idea whose time has come,” IEEE Communications Magazine, Vol. 28, No. 5, 1990, pp. 5-14. doi:10.1109/35.54342
- S. A. K. Ali, “Design and Implementation of Slantlet Based Polynomial Cancellation Coding-OFDM System using FPGA,” M.Sc. Thesis, Mustansiriya University, Baghdad, 2009.
- A. H. Kattoush, W. A. Mahmoud, A. Shaheen and A. Ghodayyah, “The Performance of Proposed One Dimensional Serial Radon based OFDM system under Different Channel Conditions,” International Journal of Computers, Systems and Signals, Vol. 9, No. 2, 2008, pp. 3-16.
- A. H. Kattoush, W. A. M. Al-Jawher, S. M. Abbas and A. T. Shaheen, “A N-Radon Based OFDM Transceivers Design and Performance Simulation over Different Channel Models,” Wireless Personal Communications, Vol. 58, No. 4, 2011, pp. 695-711. doi:10.1007/s11277-009-9902-1
- M. J. Manglani, “Wavelet Modulation in Gaussian and Rayleigh Fading Channels,” M.Sc. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, 2001.
- A. Jamin and P. Mahonen, “Wavelet Packet Modulation for Wireless Communication,” Wireless Communications and Mobile Computing Journal, Vol. 5, No. 2, 2005, pp. 123-137.
- H. J. Taha and M. F. M. Salleh, “Performance Comparison of Wavelet Packet Transform (WPT) and FFT-OFDM System Based on QAM Modulation Parameters in Fading Channels,” WSEAS Transaction on Communications, Vol. 9, No. 8, 2010, pp. 453-462.
- C. T. Man, W. Wang, Y. T. Chi and S. Wang, “The Research of OFDM Modulation and Demodulation technology Based on Wavelet Packet,” 2011 6th International Forum on Strategic technology, Harbin, 22-24 August 2011, pp. 902-906.
- A. N. Akansu, M. V. Tazebay, M. J. Medley and P. K. Das, “Waveled and Subband Transforms: Fundamentals and Communication Applications,” IEEE Communications Magazine, Vol. 35, No. 12, 1997, pp. 104-115. doi:10.1109/35.642839
- P. D. Shukla, “Complex Wavelet Transform and Their Applications,” M.Phil., University of Strathclyde, Glasgow, 2003.
- H. N. Abdullah, S. A. Jabir and A. N. Mohammed, “Complex Discrete Wavelet Transform-Based Image Denoising,” Engineering and Technology Journal, Vol. 29, No. 5, 2011, pp. 833-850.
- T. Singh, S. Chopra, H. Kaur and A. Kaur, “Image Compression Using Wavelet and Wavelet Packet Transformation,” International Journal of Computer Science and Technology, Vol. 1, No. 1, 2010, pp. 97-99.
- P.-L. Shui, Z.-F. Zhou and J.-X. Li, “Image denoising algorithm via best wavelet packet base using Wiener cost function,” IET Image Processing Magazine, Vol. 1, No. 3, 2007, pp. 311-318. doi:10.1049/iet-ipr:20060222
- M. Baro and J. Ilow, “PAPR Reduction in Wavelet Packet Modulation Using Tree Pruning,” Vehicular Technology Conference VTC2007-Spring, Dublin, 22-24 April 2007, pp. 1756-1760.

