Agricultural Sciences
Vol.06 No.10(2015), Article ID:60564,12 pages
10.4236/as.2015.610116
Variability and Synchronism of Leaf Appearance and Leaf Elongation Rates of Eleven Contrasting Rice Genotypes
Rohilyn B. Egle1, Abigail J. Domingo2, Crisanta Bueno2, Antonio C. Laurena1, Edna A. Aguilar1, Pompe Sta. Cruz1, Benoit Clerget2,3*
1Crop Science Cluster, College of Agriculture, University of the Philippines Los Baños, Laguna, Philippines
2IRRI (International Rice Research Institute), Los Baños, Laguna, Philippines
3CIRAD (Agricultural Research Centre for International Development), UMR AGAP, Montpellier, France
Email: *benoit.clerget@cirad.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 September 2015; accepted 23 October 2015; published 26 October 2015
ABSTRACT
Leaf appearance and leaf elongation rates in rice play an essential role in determining the development of the plants’ architecture which affects their adaptability to varying environments. This study aimed to characterize the rates of leaf appearance and elongation on all leaves of the main culms of rice plants for 11 contrasting varieties and to determine if the decrease in the leaf appearance rate was related to a simultaneous decrease in the rate of leaf elongation. Forty four 13-L pots were sown with one plant from one genotype and laid out in 4 randomized complete blocks. The experiment, conducted inside a greenhouse, was repeated twice. The increase in length of the leaves expanding on the main stems was monitored daily until flag leaf. Data were used to estimate the rates of leaf appearance and leaf elongation. Significant variability in the rate of leaf appearance, rate of leaf elongation, and leaf length was found across varieties. The kinetics of leaf appearance had linear phases intermediated by a curvilinear phase, without sharp changes in the phyllochron duration. Maximal leaf elongation rate (LER) of all genotypes (except for one) increased linearly with leaf rank until it reached its maximum value at leaf 8 to 10 (11 - 12 for Azucena) where it stabilized before decreasing linearly with leaf rank for the last leaves. Finally, both rates of leaf appearance and leaf elongation evolved with time more smoothly than expected so no sharp decrease in LER occurred at the time of the decrease in leaf appearance rate of the last leaves. However, the trilinear model fits the data well enough to remain useful in efficiently comparing the leaf appearance kinetics of contrasting varieties.
Keywords:
Phyllochron, Development, Flowering, Photoperiod, Oryza sativa L.

1. Introduction
Leaf appearance rate in cereal follows a regular rhythm when timed in thermal time [1] . Often, a linear correlation exists between thermal time and the number of expanded leaves on the stem, but there are also cases where bilinear or non-linear correlations are observed. Leaf appearance rate is primarily influenced by temperature but also by many other environmental factors such as water or nutrient availability and light quality [2] . It has long been established that leaf appearance rate in rice follows a three-phase kinetics. The leaves are found to appear at regular time intervals (phyllochrons) as influenced by environmental factors such as temperature, day length, mineral nutrition, light intensity, planting density, and humidity [3] . The phyllochron is shorter for the first three to five appearing leaves, intermediate for the succeeding leaves, and then longer for the last four to five leaves [4] . In aerobic conditions, the second inflection in the leaf appearance rate was also found to occur earlier with a longer phyllochron compared to flooded conditions [5] . This second decrease in the leaf appearance rate was initially believed to be associated with the panicle initiation and later with the onset of the internode elongation [6] . The physiological processes that drive regular leaf appearance and its rate changes are not known. It would be useful to fully understand these processes to be able to control them in the improvement of the adaptation of the rice plant to aerobic environments.
In rice, leaf initiation and appearance rates are strongly synchronized. The vegetative rice shoot consistently has five growing leaves at its apex: the first four are embedded into the sheaths of the already mature leaves and the fifth is expanding. It takes four phyllochrons for each newly initiated leaf to reach tip emergence and another phyllochron until collar emergence and full expansion. Specifically, at initiation, the leaf primordium is a simple protrusion at the base of the apical meristem that grows and encircles the apical dome by the beginning of the second phyllochron. The ligule and auricles initiate during the third phyllochron. At the end of the third phyllochron, when the length of the leaf blade reaches 20 mm in leaf 6, the whole leaf is composed of a single division zone where all cells divide regularly [7] . The leaf blade elongates during the fourth and fifth phyllochrons. A new elongation-only zone differentiates at the leaf tip where cell length increases eight-fold, from 10 to 80 µm. The length of this elongation zone is about 40 mm, beyond which cells are fully matured. Blades then start to elongate faster, pushing up the leaf tip that emerged from the sheath of leaf 5 at the end of the fourth phyllochron. At this time, the blade length of leaf 6 has attained about 100 mm. Fournier et al. [8] showed in maize that the leaf elongation rate (LER) variation goes through four phases related to blade meristem activity. During the first phase, LER increases exponentially as a result of cell divisions only. The second phase is a short transition during which the elongation zone is established. During the third phase, LER becomes stable at its maximum value due to the balance between the number of incoming and exiting cells of the elongation zone. The fast appearance of the leaf blade is then mainly caused by the simultaneous elongation of a large number of cells (2000 - 2500 cells) per file and per day to reach the observed elongation which is up to 20 cm per day [9] . During the fourth phase, LER quickly drops to zero after the termination of the activity of the division zone. It was also found that synchronies exist between emergence events and phase changes. In wheat, the end of the first phase of leaf (n) coincides with the emergence of the collar of leaf (n-2). Likewise, in many cereals, the end of the second phase coincides with the appearance of the leaf tip whereas the end of the third phase is synchronous with the appearance of the leaf collar. These synchronies suggest that emergence events trigger the changes of phase in the meristem, consequently controlling the phyllochron.
A previous experiment showed that a trilinear model fits the leaf appearance kinetics of the NSIC RC222 rice variety better than two other curvilinear models [10] - [12] . The phyllochron had a value of 63˚Cd until the appearance of leaf 11 and 143˚Cd afterwards. However, leaf 12 has already undergone three phyllochrons and close to starting to elongate when leaf 11 appeared. It was thus hypothesized that the sharp breaking of the broken-linear model would be the result of a sharp reduction in the rate of elongation of leaf 12 compared with leaf 11, such that the phyllochron has more than doubled after the appearance of leaf 11. This implies that during the last phase of vegetative development, not only the rate of new leaf initiation by the apical meristem was reduced but also the rate of cell elongation in the intercalary meristems of the leaf blades. If this is true, it would signify that a systemic physiological reaction affected the plant at the time of the abrupt change of the phyllochron, involving processes as different as the rate of primordia initiation by the stem apex and the cell capacity to elongate. This experiment was designed to analyse the variability of the rate of elongation of the successive leaves on the main stem of contrasting genotypes and to test the hypothesis of synchronism between the breaking points in the leaf appearance kinetics and the profile of the leaf elongation rates.
2. Materials and Methods
2.1. Treatments and Experimental Design
The study was conducted in a greenhouse facility at IRRI, Los Baños, Philippines (14˚11'N, 121˚15'E) on June 6, 2013 and repeated on September 19, 2013. Eleven contrasting rice varieties were used, namely Hong Zui Zao and E 5168 (early-maturing indica); IR 72, NSIC Rc 222 and PSB Rc 18 (medium-maturing indica); Sahelika and WAS 203-B-B-2-4-1 (late-maturing indica); Azucena and IR 78049-25-2-2-2 (late tropical japonica); and Mestizo 7 and Mestizo 30 (intermediate indica hybrids). Seeds were obtained from the IRRI rice gene bank.
Two weeks prior to sowing, 44 large pots (13 L buckets) were filled with soil from an irrigated lowland rice field and were irrigated and arranged into four lines (replications) with eleven pots each. Weeds were uprooted daily until little to no weeds emerged. Three days before sowing, the seeds were soaked for 24 hours and then incubated at 30˚C for 48 hours. Three germinated seeds from each variety were planted, one variety for each pot. Each pot was applied with basal fertilizers (3.6 g Solophos, 0.56 g Muriate of Potash, and 0.32 g ZnSO4 per pot) and then flooded. Soil aerobic conditions were maintained through daily irrigation for the entire germination period. Ten days after sowing (DAS), the pots were thinned to have one plant each and water level was maintained at approximately 3 cm above the soil surface. Urea (0.6 g per pot) was applied on the first, fifth, and eighth week after planting. Authorized insecticides (Cypermethrin, Cartap) were applied when required.
2.2. Data Collection and Analysis
Leaves of the main tiller were tagged and measured every day at early morning from the day the tips emerged out of the whorl. The leaves of the main stem were numbered according to their order of appearance and new developing leaves were tagged at their visible base with respect to a reference. For leaves 3 to 7, the reference was the collar of the previous leaf (n-1; n is the leaf being measured). For leaf 8 onwards, the collar of leaf n-1 starts appearing a day later than the new leaf. Hence, starting leaf 8, the reference was the collar of leaf n-2 instead of leaf n-1. The distances between two successive tags based on these references were measured with a ruler to determine the leaf growth for the day. The exact time of every tagging was consistently noted for calculating the leaf growth rate later.
Soil temperature was constantly monitored using three thermocouples (PyroControle, Vaulx en Velin, France) installed at a 2-cm depth in three pots chosen randomly. Solar radiation was measured using a pyranometer (LI-200, Li-Cor, Lincoln, NE, USA) while air temperature and relative humidity were measured using a hygrometer (HMP 45C, Vaisala, Helsinki, Finland). Both sensors were installed at a 2-m height. The data were stored in a datalogger (CR10X, Campbell Scientific, Logan, UT, USA).
The date of appearance of each leaf was extracted from the data set as the first date of measurement of leaf elongation. A decimal estimation of the appeared leaf number was then calculated through a method similar to Haun’s stage determination method [13] . It is the number of the currently appearing leaf plus the ratio between the current length of the blade and its final total length. Thermal time (TT) was calculated as the cumulative sum of the mean daily temperature of the apical meristem minus the base temperature of 11˚C starting from the day of emergence up to the day of measurement. The temperature of the apical meristem was expected to be equal to the soil temperature until the onset of stem elongation and then to the temperature at the 2-m height.
Bilinear and trilinear segmented models were tried and compared to determine the best model for the dynamics of leaf development. The observed leaf number (LN) was regressed against the elapsed TT first by using a bilinear equation (1)
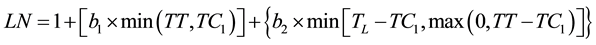 (1)
(1)
and then by using a trilinear equation (2)
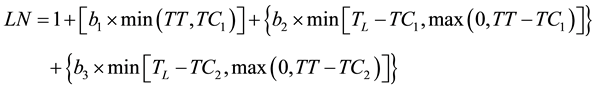 (2)
(2)
where TC1 and TC2 are the thermal times when the development rate changed and TL is the thermal time when the last leaf appeared. The parameters and their confidence intervals were the optimum estimates from the successive iterations of the SAS NLIN [14] procedure used to model the data with bilinear and trilinear equations. The fit of the resulting equations was compared using the pseudo-F (Equation (3)):
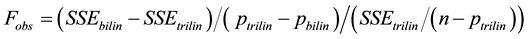 (3)
(3)
where SSEbilin and SSEtrilin are the sums of the square error of the bilinear and trilinear models, respectively; n is the number of observations; and pbilin and ptrilin are the number of parameters of their corresponding models [10] . Randomness of the residuals was tested using a Wald-Wolfowitz (or Runs) test [15] .
The combined curvilinear and linear models were also tested for their ability to fit the data. These models were formed based on the curvilinear model proposed by Yin and Kropff [12] and the fact that the appearance of the last leaves is linear. In order to improve the flexibility in modelling the bend of the curve, an additional parameter (a) was added to the equation. The first model (curvilinear 2, Equation (4)) assumed that the dynamics of leaf appearance starts as curvilinear and then eventually becomes linear:
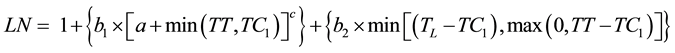 (4)
(4)
where 1 is the number of leaves at emergence; b1, a, and c are coefficients; b2 is the rate of development of the last leaves; TC1 is the thermal time when the dynamics changed from curvilinear to linear; and TL is the thermal time when the last leaf appeared.
The second model (curvilinear 3, Equation (5)) considered that the first leaves appear faster with possible linear dynamics. This model thus started as linear, then became curvilinear and then linear again:
 (5)
(5)
where b1 is the initial rate of development and TC1 is the thermal time when the development dynamics changed from linear to curvilinear. The last model (curvilinear 4) was designed like curvilinear 2 with the addition of two initial linear segments before the curvilinear and the last linear segment. The ability of these models to fit the data was compared using the pseudo-F statistic defined previously.
The phyllochrons at the time of appearance of each leaf were calculated as the inverse of the value of the derivative of the equation that best fit the data for each variety at each sowing date for the corresponding sum of temperature. The daily leaf elongation rate (mm・˚Cd−1) was computed as equation (6):
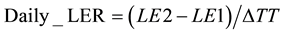 (6)
(6)
where LE1 and LE2 are the leaf length (mm) from the tip at time 1 and time 2, respectively, and ΔTT is the difference between the thermal times at time 2 and time 1 (˚Cd). The higher of the two first measurable Daily_LER was extracted from the computed data as the maximal rate of the leaf blade elongation and was referenced as LER.
To test the significance of the differences in the rate of leaf appearance observed across varieties, data for LN during the second linear segments of the trilinear model until TC2-200˚Cd and during the third segment from TC2+200˚Cd were extracted per variety from the datasets. The regressions between LN and TT were compared across varieties using Analysis of Variance [14] . Similarly, in order to test the significance of the differences in the LER and leaf length observed by leaf rank across varieties, data from the first increasing part of the profiles until the maximum value was reached was selected. ANOVA was performed on this dataset to test the significance of the sowing date, genotype, leaf rank, and their interactions as sources of variation. Means per genotype were then grouped using the Student-Newman-Keuls (SNK) stepwise multiple comparisons procedure.
3. Results
3.1. The Greenhouse Climate
Temperature values were almost constant throughout the experimental period, with mean air temperatures of 29.2˚C and 28.1˚C and mean soil temperatures of 30˚C and 28.8˚C for the June and September sowings, respectively (Figure 1). The average relative humidity was the same (72.5%) for both sowing dates while the mean photosynthetically active radiation (PAR) transmitted into the greenhouse was higher for the June (4.8 MJ・m−2) than for the September sowing (3.5 MJ・m−2). Day lengths were also longer for the June sowing, evolving from 1251 h at sowing to a maximum of 1253 h on June 21 and decreasing to 1223 h at the end of the experiment. For the September sowing, it decreased from 1207 h at sowing to 1119 h at flag-leaf appearance.
3.2. Leaf Appearance Kinetics
The trilinear model fit the data well and consistently across all varieties. After a fast appearance of the first four to five leaves, the rate of leaf appearance decreased once and remained stable until a second decrease, affecting the appearance of latter leaves for all genotypes and the two sowing dates (Figure 2). On the average, the length of time until flag-leaf appearance was shorter by 280˚Cd for the second sowing. The main stems of plants grown in September developed 2.2 leaves less than those planted in June, with large differences among varieties: from 0.9 leaves for WAS 203-B-B-2-4-1 to 2.9 for PSB Rc18. Nevertheless, the leaf appearance kinetics by variety was very similar between sowing dates. Data for all varieties in both sowing dates were better fitted by a trilinear than by a bilinear model (Table 1). However, as shown for the variety NSIC Rc222 sown in June, the trilinear model did not generate randomly distributed mean residuals (Figure 3 (a) and Figure 3(c); Wald-Wolfowitz Z = 6.50, P < 0.0001). The curvilinear 2 model gave a better fit of the data with smaller but not randomly distributed residuals for 9 out of 10 varieties for the first sowing and 7 out of 11 varieties for the second sowing. No significant improvement in the data fitting was observed when curvilinear 3 was used instead of the curvilinear 2 model. Meanwhile, significant improvement in the data fitting was found in five varieties in the first sowing and seven varieties in the second sowing when the curvilinear 4 model was used instead of curvilinear 2. Otherwise the two models performed equally well. The distribution of mean residuals was significantly randomly distributed when the curvilinear 4 model was used (Figure 3 (b) and Figure 3(d); Wald-Wolfowitz Z = 1.59, P = 0.11).
The varieties Sahelika, NSIC Rc222, and Mestizo 7 developed leaves faster than the other varieties for both sowing dates, whereas IR 78049-25-2-2-2 developed leaves consistently slower (Figure 2). The result of the
Figure 1. Daily average of greenhouse climatic variables for the June and September 2013 sowing: (a) Air temperature, (b) Soil temperature, (c) Relative humidity, and (d) Photosynthetically active radiation.
Figure 2. Predicted appeared leaves of the eleven varieties sown on June (a) and September (b) 2013 using the trilinear model. Mean of the observed values for Sahelika and IR 78049-25-2-2-2 on June sowing were superimposed on the predicted values to show the actual fit of the models.
Figure 3. Comparison of the fit and daily mean residual between the trilinear (a) and (c) and curvilinear4 (b) and (d) models for NSIC Rc222 sown on June 2013.
Analysis of Variance done on the regressions between the number of appeared leaves and thermal time showed significant genotype and thermal time interactions for the second and third segments of the trilinear model at both sowing dates (Table 2). This supports the existence of significant differences among genotypes for the rate of leaf appearance during the second and third phases of the trilinear developmental kinetics. Significant positive relationships were found between the two successive rates of leaf appearance, during the second and third segments, on both sowing dates (Slope = 2.40, r2 = 0.45, P = 0.03 for June sowing; Slope = 1.84, r2 = 0.68, P = 0.002 for September sowing).
3.3. Leaf Elongation Rate
The daily leaf elongation rates recorded were generally highest in the first day of measurement and then regularly decreasing for the succeeding days (Figure 4). For early leaves with short blades, the length of the blade
Figure 4. Daily LER recorded per leaf, from 3 to 19, of one plant of the variety NSIC Rc222 for the June 2013 sowing.
Table 1. SSE reduction among models tested on the eleven varieties sown on June and September 2013.
***: Significant at 0.001.
Table 2. ANOVA for comparing the slope of the second and third segments of the trilinear models for the leaf appearance of eleven varieties sown on June and September 2013.
was similar to the length of the previous sheath, hence, only the sheath elongation was actually observed even during the first day of recording. For later leaves with longer blades (leaves above rank 5 to 6), leaf blades were still growing, one to three days after the appearance of the leaf tip, and then only sheath elongation was recorded. The maximum leaf elongation rate (LER) regularly increased with the leaf rank until it reached a maximum value between leaf 8 and 10, depending on the variety (Figure 5(a) & Figure 5(b)). The LER then either remained stable with leaf rank in late varieties or started decreasing in early varieties. These observed trends were consistent across the two sowing dates. Based on the graphs, the leaf blades of Azucena, a tropical japonica landrace, elongated significantly faster than the leaves of all the other varieties. This was confirmed by the comparison of the mean LERs of the first leaves until the leaf with maximum LER value (Table 3): The mean LER of Azucena was significantly higher than all the other varieties. It was followed by Sahelika and a very early-maturing variety, Hong Zui Zao. In contrast, the leaf blades of IR 78049-25-2-2-2 and E 5168 grew significantly slower. The other five varieties formed two intermediate, less differentiated groups.
3.4. Leaf Length and Relationship with Leaf Elongation Rate
The longest leaf preceded the last four leaves (growing after panicle initiation) in all varieties except for the two
Figure 5. Behavior of the maximum leaf elongation rate (LER) ((a) and (b)) and of the leaf blade length ((c) and (d)) on the main stem through increasing leaf rank and the interaction between these two traits ((e) and (f)) for all leaves before the appearance of the longest leaf across varieties for the June and September 2013 sowing. For the variety Azucena, the interaction in the last upper leaves was plotted with a dashed line.
Table 3. ANOVA for comparing the LER and leaf length per sowing date, genotype and leaf rank, and comparison of the means per genotype. Means followed by the same letter are not significantly different.
very early-maturing varieties Hong Zui Zao and E 5168, whose longest leaf immediately preceded the flag leaf (Figure 5(c) & Figure 5(d)). Two varieties (Azucena and PSB Rc18) had significantly longer mean leaf lengths than the other varieties until maximum length (Table 3). ANOVA on leaf length showed that the sowing date, genotype, leaf rank, and all their interactions were highly significant.
The relationship between the LER and the blade length per leaf showed three distinct phases (Figure 5(e) & Figure 5(f)). During the first phase, the LER and blade lengths were positively correlated until the LER reached its maximum value around leaf 8 to 10, depending on the variety. During the second phase, the LER kept a stable maximum value while the length of the blade continued to increase. During the third phase (only plotted for Azucena), the LER and blade length of the last two to four leaves of the main stem were also positively correlated albeit differently from the first phase. Indeed, the LER of these latter leaves was much slower than the LER of the early leaves with a similar final blade length. Except in IR 78049-25-2-2-2, there was a strong positive linear relationship between the means of LER and leaf length (r2 = 0.82, P = 0.0003) such that genotypes developing longer leaves showed faster mean LER.
3.5. Synchronicity of the Changes of Phyllochron and the Decrease in the LER of Last Leaves
In all varieties and sowing dates the leaf that appeared at the end of the curvilinear phase in the curvilinear4 model was of higher rank than the leaf with faster LER (Figure 6). The leaf with faster LER, however, was regularly closely ranked with the leaf that appeared at the time of the second inflection point in the trilinear model. LER decreases between two consecutives leaves sharp enough to be significant were rare and only occurred
Figure 6. Synchronism in leaf appearance kinetics (red symbols) and changes in LER trend (green symbols) relative to leaf rank across the different growth phases per variety for the June (a) and September (b) sowing. Varieties were sorted by total leaf number.
during the last linear phase of the curvilinear4 model and thus only concerned late appearing leaves simultaneously growing with the panicle. The sequence of events was clearer when plants developed 15 or more leaves.
4. Discussion
4.1. Effects of Day Length and Seasonal Weather
All ten varieties, including the very early-maturing variety Hong Zui Zao, developed more leaves and flowered later for the June sowing as a response to the season’s longer photoperiod as compared to the September sowing. The effect of photoperiod on the duration to flowering time is well documented [16] - [18] but only a few references regarding the corresponding variation in leaf number exists [6] , [19] . The large difference in leaf count between the two sowing dates induced a shift in the leaf length and LER profiles. It was thus not appropriate to average these results into a common analysis; instead, the results were reported separately by sowing date.
On the other hand, leaf appearance rate was found to be similar between the two sowing dates for nine varieties except for the appearance rate of leaves 4 and 5 which were slower in September. It may be possible that this was caused by the lower solar radiation due to cloudy weather in September received by the plants during the first 10 days of their life (Figure 1).
4.2. Leaf Appearance Kinetics was Partially Curvilinear and Variable across Varieties
In a previous paper, Clerget and Bueno [10] reported a pot experiment in the same greenhouse in which the weekly recorded data were better fitted to a broken linear than two curvilinear models [11] , [12] . In this current experiment which used daily recorded data, the trilinear model gave an acceptable fit but with a non-random distribution of the residuals (Figure 2 and Figure 3). Indeed, the predicted values consistently digressed from the observed values upon approaching the breaking points. The possibility that this effect could result from the variability between the four measured plants was checked and it was found that for all varieties except Azucena, the development of the plants and of their leaves was very similar across the four replicated pots. Models with increasing numbers of linear segments were then tested until curvilinearity had to be re-evaluated in agreement with McMaster [3] who opposed the linear relationships observed in field experiments based on non-linear relationships recorded in growth chambers and greenhouses.
Since the previous attempt of our group to fit previously defined curvilinear models had been unsuccessful, a closer analysis of the data was done to find the reason for the bad fit and to determine which modifications could be done to improve the fit. Apparently, the curvilinear models could not fit well because the last part of the recorded leaf appearance kinetics was clearly linear. This was consistent with the reported leaf appearance kinetics in photoperiod-sensitive sorghum during the last phase which lasts up to six months [20] . A two-phase model comprised by a curvilinear phase followed by a linear phase (curvilinear 2) was then tried and was found to fit the data better than the trilinear model except for the early maturing varieties Hong Zui Zao and E 5168 (Table 1). Another model was formulated which took account of the fast linear rate of appearance of the first leaves that were already pre-existing in the embryo (curvilinear 3). However, this model did not bring any significant improvement to curvilinear 2. Finally, a model with two initial linear segments followed by a curvilinear period and then a last linear segment was designed (curvilinear 4). This fit the data as well as or significantly better than curvilinear 2. Curvilinear 4 was thus a compromise between the assumption of stable phyllochrons and the curvilinear theory.
The justification for the curvilinearity was that later-appearing leaves take more time to appear because the distance that each leaf tip has to traverse from the apical meristem to the whorl increases for every subsequent leaf [11] . Curvilinear 4 still took into account the old observation of the faster appearance of the first leaves and hypothesized that phyllochrons were fundamentally stable but different for the first and for latter leaves. It also added a transitional period between the two phases of stable phyllochrons during which the phyllochron gradually increased leaf after leaf. However, these observations were derived from plants grown in pots and in artificial conditions such as the case of Yin and Kropff [12] and Streck et al. [11] . It should be verified that temporary curvilinearity also applies to plants grown in the field under natural conditions.
4.3. Maximum Rate of Elongation and Length of the Blade of Each Leaf
In previous studies, leaf elongation rate was generally recorded for one or few consecutive early leaves of the main stem in order to study how it is affected by various factors. But for this experiment, daily recorded data described the maximum rate of elongation (Figure 5(a) and Figure 5(b)) of the blade for each leaf of the main stem of 11 rice varieties under optimal growing conditions. Such information on the whole LER profile can be found in the literature for one variety of sorghum [21] while the variability for LER across rice varieties had been studied for just leaf 6 of seven rice varieties [7] . The latter study showed that LER for leaf 6 is around 2 mm h20˚C-1. This is equivalent to 5.3 mm・˚Cd−1 with a base temperature of 11˚C and in agreement with the value from this experiment. Complete LER profiles of the main stem as presented here confirmed varietal differences for this trait. Some varieties had faster LER than others at any leaf rank above leaf 3.
Two varieties, Azucena and PSB Rc18 had significantly longer leaves than other varieties while Azucena, Sahelika, and Hong Zui Zao had faster LER (Table 2). All the interactions among the sources of variation in the ANOVA were significant although, differences in the mean LER across genotypes were most likely caused by the faster increases of LER with leaf rank in some genotypes given that the LERs for the first leaves were small and similar for all genotypes (Figure 5(a) and Figure 5(b)). Statistical translation of this variable relationship is a significant genotype x leaf rank interaction for LER, thus directly linked with the significant differences between LER means. Here the significant interaction supports the interpretation that difference in means was due to the differences in genotype. All the other interactions were influenced by the sowing date which modified the total number of leaves and consequently the shape of the leaf length and LER profiles. It is thus possible to conclude based on the statistical grouping of genotypes according to their mean LER which agrees with the graphical observation.
The genotype Azucena had much longer leaves expanding faster than all the other varieties. Azucena is a tropical japonica variety known for its drought tolerance and its deeper rooting system and has been used in many research works. It was also in the group with faster LER in the study of Parent et al. [7] when the seven varieties were separated into two distinct groups based on the LER of leaf 6. IR 64 (another IRRI variety similar to the IR 72 variety used in this experiment), on the other hand, was in the group with slower LER like IR 72 was in the current experiment. IR 78049-25-2-2-2 was at the other extremity: this genotype had longer leaves than others at comparable LER.
4.3. Changes in Rates of Leaf Appearance and Leaf Elongation Were Not Correlated
The initial hypothesis of simultaneous decrease of the rates of leaf appearance and leaf elongation was not supported by the results of the experiment despite the recurrent observable synchrony between the predicted leaf rank at the second inflection point of the trilinear model and the rank of the longer leaf. The hypothesis that there is a sudden reduction of the phyllochron between two linear periods with stable phyllochron was disproved when curvilinear phase showed a more accurate representation of the changes that were in fact gradual. No significant decrease in the LER between two consecutive leaves was observed around neither the initially expected breaking point of the leaf appearance kinetics nor the appearance of leaf 12 nor at the time of the now delayed breaking point between the curvilinear and the last linear phases. Consequently, no sharp reduction in LER, which eventually means of the rates of cell multiplication and cell elongation in the intercalary blade meristem, was involved in the sudden change of the leaf appearance rate. The internal coordination between the leaf appearance rate and the LER was mainly caused by gradual changes in both rates from one leaf to another. This result brings new information on the relationship between the phyllochron and the rate of leaf elongation that will be useful to calibrate a model relating the plastochron and the phyllochron. Specifically, it shed light on how the phyllochron of the last leaves remained stable while their length sharply decreased. Lastly, an important consideration is that LER is fast with regards to the length of the sheaths to be traversed before the leaf tip emerged. For instance, since the LER of leaf 6 was about 5 mm・˚Cd−1 (Figure 5(a) & Figure 5(b)) and the sheath length of leaf 5 was around 100 mm (data not shown), it takes only 20˚Cd to traverse the entire sheath length at maximum LER while the phyllochron of leaf 6 remains at about 50˚Cd (data not shown). Evidently, even a significant change in LER would not significantly affect the duration of the phyllochron whose regulation probably depends more on the triggering of the switch to cell elongation in the leaf meristem, as already pointed out by Fournier et al. [8] .
5. Conclusion
The significant genetic variability found across the 11 varieties tested could allow plant breeding for the rate of leaf appearance, the LER, and the blade length profiles in the future. The kinetics of leaf appearance was found partially curvilinear in this experiment carried out in pots in a greenhouse and with daily data recording. The initial hypothesis of a sharp change in the rate of leaf appearance at about the time of appearance of leaf 12 was disproved and no more relationship with a sharp modification in the LER could be expected. The coordination between leaf appearance and elongation rates came from gradual instead of sharp changes in both rates, leaf after leaf. Although not the better model, broken-linear model will be sufficiently accurate to sort varieties phenotyped for their rate of leaf appearance.
Acknowledgements
We thank Pedro Gapas who was in charge of the operational support for this experiment, the other members of the Ecophysiology Team at IRRI Rene Carandang, Luis Malabayabas, and Victor Lubignan for additional assistance, and Michael Dingkhun and Anne Lasam for editing.
Cite this paper
Rohilyn B.Egle,Abigail J.Domingo,CrisantaBueno,AntonioC. Laurena,Edna A.Aguilar,PompeSta. Cruz,BenoitClerget, (2015) Variability and Synchronism of Leaf Appearance and Leaf Elongation Rates of Eleven Contrasting Rice Genotypes. Agricultural Sciences,06,1207-1219. doi: 10.4236/as.2015.610116
References
- 1. Rickman, R.W. and Klepper, B.L. (1995) The Phyllochron: Where Do We Go in the Future? Crop Science, 35, 44-49.
http://dx.doi.org/10.2135/cropsci1995.0011183X003500010008x - 2. Wilhelm, W.W. and McMaster, G.S. (1995) Importance of the Phyllochron in Studying Development and Growth in Grasses. Crop Science, 35, 1-3.
http://dx.doi.org/10.2135/cropsci1995.0011183X003500010001x - 3. McMaster, G.S. (2005) Phytomers, Phyllochrons, Phenology and Temperate Cereal Development. Journal of Agricultural Science, 143, 137-150.
http://dx.doi.org/10.1017/S0021859605005083 - 4. Nemoto, K., Morita, S. and Baba, T. (1995) Shoot and Root Development in Rice Related to Phyllochron. Crop Science, 35, 24-29.
http://dx.doi.org/10.2135/cropsci1995.0011183X003500010005x - 5. Clerget, B., Bueno, C., Quilty, J.R., Correa Jr., T.Q. and Sandro, J. (2014) Modifications in Development and Growth of a Dual-Adapted Tropical Rice Variety Grown as Either a Flooded or an Aerobic Crop. Field Crops Research, 155, 134-143.
http://dx.doi.org/10.1016/j.fcr.2013.09.013 - 6. Yoshida, S. (1981) Fundamentals of Rice Crop Science. The International Rice Research Institute, Los Baños.
- 7. Parent, B., Conejero, G. and Tardieu, F. (2009) Spatial and Temporal Analysis of Non-Steady Elongation of Rice Leaves. Plant, Cell and Environment, 32, 1561-1572.
http://dx.doi.org/10.1111/j.1365-3040.2009.02020.x - 8. Fournier, C., Durand, J.L., Ljutovac, S., Schaüfele, R., Gastal, F. and Andrieu, B. (2005) A Functional-Structured Model of Elongation of the Grass Leaf and Its Relationships with the Phyllochron. New Phytologist, 166, 881-894.
http://dx.doi.org/10.1111/j.1469-8137.2005.01371.x - 9. Egle, R.B. (2014) Synchronism of Leaf Development and Leaf Elongation Rates of Contrasting Rice (Oryza sativa L.) Genotypes. M.Sc. Thesis, University of the Philippines Los Baños.
- 10. Clerget, B. and Bueno, C. (2013) The Effect of Aerobic Soil Conditions, Soil Volume and Sowing Date on the Development of Four Tropical Rice Varieties Grown in the Greenhouse. Functional Plant Biology, 40, 79-88.
http://dx.doi.org/10.1071/FP12194 - 11. Streck, N.A., Bosco, L.C. and Lago, I. (2008) Simulating Leaf Appearance in Rice. Agronomy Journal, 100, 490-501.
http://dx.doi.org/10.2134/agronj2007.0156 - 12. Yin, X. and Kropff, M.J. (1996) The Effect of Temperature on Leaf Appearance in Rice. Annals of Botany, 77, 215-221.
http://dx.doi.org/10.1006/anbo.1996.0025 - 13. Haun, J.R. (1973) Visual Quantification of Wheat Development. Agronomy Journal, 66, 116-119.
http://dx.doi.org/10.2134/agronj1973.00021962006500010035x - 14. SAS (2008) SAS Online® 9.2. SAS Institute Inc., Cary, NC.
- 15. Wald-Wolfowitz (or Runs) Test for Randomness, Knowledge Base/Samples & SAS Notes.
http://support.sas.com/kb/33/092.html - 16. Fukai, S. (1999) Phenology in Rainfed Lowland Rice. Field Crops Research, 64, 51-60.
http://dx.doi.org/10.1016/S0378-4290(99)00050-7 - 17. Vergara, B.S. and Chang, T.T. (1985) The Flowering Response of the Rice Plant to Photoperiod: A Review of the Literature. 4th Edition, International Rice Research Institute, Los Baños.
- 18. Kawakata, T. and Yajima, M. (1995) Modeling Flowering Time of Rice Plants under Natural Photoperiod and Constant Air-Temperature. Agronomy Journal, 87, 393-396.
http://dx.doi.org/10.2134/agronj1995.00021962008700030001x - 19. Sié, M., Dingkuhn, M., Wopereis, M.C.S. and Miezan, K.M. (1988) Rice Crop Duration and Leaf Appearance Rate in a Variable Thermal Environment: I. Development of an Empirically Based Model. Field Crops Research, 57, 1-13.
http://dx.doi.org/10.1016/S0378-4290(97)00110-X - 20. Clerget, B., Dingkuhn, M., Gozé, E., Rattunde, H.F.W. and Ney, B. (2008) Variability of Phyllochron, Plastochron and Rate of Increase in Height in Photoperiod-Sensitive Sorghum Varieties. Annals of Botany, 101, 579-594.
http://dx.doi.org/10.1093/aob/mcm327 - 21. Lafarge, T. and Tardieu, F. (2002) A Model Co-Ordinating the Elongation of All Leaves of a Sorghum Cultivar Was Applied to Both Mediterranean and Sahelian Conditions. Journal of Experimental Botany, 53, 715-725.
http://dx.doi.org/10.1093/jexbot/53.369.715
NOTES

*Corresponding author.








