Agricultural Sciences
Vol.5 No.4(2014), Article ID:43987,12 pages DOI:10.4236/as.2014.54035
Rice Green Revolution and Climatic Change in East Africa: An Approach from the Technical Efficiency of Rainfed Rice Farmers in Uganda
Atsushi Maruyama1, Yusuke Haneishi1,2, Stella E. Okello3, Godfrey Asea3, Tatsushi Tsuboi2, Michiko Takagaki1, Masao Kikuchi1
1Graduate School of Horticulture, Chiba University, Matsudo, Japan
2JICA Uganda Office, Kampala, Uganda
3National Crops Resources Research Institute, Kampala, Uganda
Email: a.maruyama@faculty.chiba-u.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 19 December 2013; revised 22 February 2014; accepted 8 March 2014
ABSTRACT
In East Africa where a drastic improvement in food security is an urgent need, rice, a non-traditional crop in most of countries in the region, has emerged as an important food crop that could extend the Green Revolution to the region following the introduction of New Rice for Africa (NERICA) in the early 2000s. Using data collected through a nationwide survey, this paper examines the possibility of rice green revolution by estimating the technical efficiency (TE) of rainfed rice farmers in Uganda and simulates how unfavorable climate changes affect it. The estimated stochastic frontier yield function showed that the mean TE was 65% for lowland and 60% for upland, and that the potential yield of rainfed rice cultivation was as high as 3 t·ha−1. However, the stochastic simulation of rainfall and rice yield revealed that unfavorable climate changes could erase the high potential in crop yield. Rainfed rice cultivation could be a leading sector for realizing Green Revolution in East Africa. It plays a critical role in this process to improve rice farmers’ TE, which is lower in the region than in Asia. Worsening climatic conditions, if occur, make this need even more imperative.
Keywords: Sub-Saharan Africa; Green Revolution; Yield Function; Stochastic Frontier; Stochastic Simulation; Climate Change

1. Introduction
A Green Revolution has long been awaited in sub-Saharan Africa (SSA), particularly in East Africa where a drastic improvement in food security is an urgent need. Since the introduction of New Rice for Africa (NERICA) in the early 2000s, rice has emerged as an important food crop that could extend the Green Revolution to the region [1] -[3] .
As is well known, the Green Revolution in rice was brought in Asia half a century ago by technological breakthroughs that increased the yield of irrigated lowland rice cultivation [1] [3] [4] . In East Africa, irrigated lowland is virtually non-existent [5] and the prospect of large-scale irrigation development, a key concomitant development with the Green Revolution in Asia, is seriously constrained by its economic infeasibility [6] . The agro-climatic, ecological and geographical conditions of SSA, however, provide a vast amount of land for rainfed rice cultivation in many inland valleys in the hydromorphic valley bottoms and the lower parts of the valley slope adjacent to the hydromorphic edge [5] . It is in this context that NERICA, which fits wetland as well as dry land conditions, is welcomed as an agent to promote a Green Revolution in rainfed rice cultivation.
Extending the Green Revolution to rainfed rice cultivation would be a particularly vital achievement in SSA that faces severe environmental conditions vulnerable to future climatic changes. Many climate studies predict that the variability and uncertainty in rainfall in the region will increase in the future [7] -[9] . Under such circumstances, whether NERICA or any other modern varieties can bring a sustainable breakthrough in the yield of rainfed rice cultivation is crucially important in determining the direction and priority of agricultural research, as well as the agricultural development policies of the countries in the region and international aid agencies pursuing Green Revolutions in SSA. For instance, some recent studies have expressed skepticism as to the possibility of attaining a Green Revolution based on rainfed rice cultivation [10] , or have begun to reexamine the possibility of Green Revolution based on irrigated lowland cultivation in large-scale irrigation schemes [11] [12] .
The purpose of this paper is to assess the yield potential of rainfed rice cultivation in farmers’ fields by estimating the technical efficiency (TE) of rainfed rice farmers in Uganda based on the data collected through a nationwide survey. We first estimate TE under the present climatic conditions by applying the stochastic frontier rice yield function and then conduct simulation analyses with a stochastic simulation model to examine how the yield potentials change as climatic conditions and TE change. The results will indicate whether a rice Green Revolution based on rainfed rice cultivation with the current potential is possible in East Africa and what factors are required to realize it.
2. Methods and Materials
2.1. Stochastic Frontier Analysis
In this paper, the yield potential of rainfed rice cultivation is analyzed by means of stochastic frontier yield functions that measure farmers’ TE in rice cultivation. TE in this paper is defined as the measure of the ability of a farmer to attain the maximum yield for a given set of inputs [13] . There are a few methods for estimating TE [14] , of which this paper adopts the stochastic frontier function approach [15] [16] , taking into account that rainfed rice cultivation is subject to large weather disturbances and heterogeneous environmental factors.
The stochastic frontier rice yield function is defined as follows:
 . (1)
. (1)
where Yi is the rice yield per hectare of the i-th farmer, Xi is a (1 × k) vector of inputs per hectare of the i-th farmer, Zi is a (1 × m) vector of critical natural conditions such as precipitation, β is 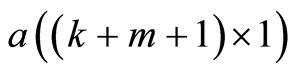 vector of unknown parameters, f( ) is the frontier yield function that gives the maximum potential yield for any particular input vector, Vi is the random error independently and identically distributed with
vector of unknown parameters, f( ) is the frontier yield function that gives the maximum potential yield for any particular input vector, Vi is the random error independently and identically distributed with 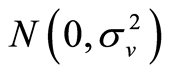 and independent of Ui, and Ui is the independently and identically distributed non-negative random error with a mean of either 0 or a non-zero value μi which reflects the i-th farmer’s technical inefficiency [16] [17] . The error term Vi represents purely random disturbances that occur beyond the control of individual farmers, and therefore can take either a positive or negative value. The error term Ui takes only a positive value, representing a downward deviation from the frontier yield attributable to technical inefficiency, and the TE of the i-th farmer is given as
and independent of Ui, and Ui is the independently and identically distributed non-negative random error with a mean of either 0 or a non-zero value μi which reflects the i-th farmer’s technical inefficiency [16] [17] . The error term Vi represents purely random disturbances that occur beyond the control of individual farmers, and therefore can take either a positive or negative value. The error term Ui takes only a positive value, representing a downward deviation from the frontier yield attributable to technical inefficiency, and the TE of the i-th farmer is given as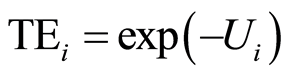 . We estimate Equation (1) by the maximum-likelihood method assuming that Ui follows an exponential distribution. In addition to the estimation using the entire sample, the yield function is also estimated separately for lowland and upland, and whether the estimated coefficients have equal impacts on yield between the two land types is tested by the seemingly unrelated regression (SUR) method. All regression analyses are carried out using STATA 12 (StataCorp LP, College Station, TX).
. We estimate Equation (1) by the maximum-likelihood method assuming that Ui follows an exponential distribution. In addition to the estimation using the entire sample, the yield function is also estimated separately for lowland and upland, and whether the estimated coefficients have equal impacts on yield between the two land types is tested by the seemingly unrelated regression (SUR) method. All regression analyses are carried out using STATA 12 (StataCorp LP, College Station, TX).
2.2. Stochastic Simulation Analysis
To understand the potential impacts of changes in rainfall and TE on rice yield, we conduct simulation analyses to generate the mean yield and the distribution of the yield, based on the estimated parameters of the frontier production function and the fitted stochastic distributions of the number of below-minimum-rainfall (BMR) days, which shall be explained in detail in the next subsection, and TE.
For BMR days, the stochastic distribution is set as follows: first, fit a stochastic distribution to daily rainfall data by using a goodness of fit standard (Kolmogorov-Smirnov test), second, calculate the occurrence rate of BMR days from the simulated rainfall data, third, calculate the number of BMR days by multiplying the occurrence rate by 30 days per month, and fourth, identify a better fitting stochastic distribution for the BMR day data. For TE, a better fitting stochastic distribution is identified similarly from among several possible distributions. The procedure to find a good fitting stochastic distribution is necessary, notwithstanding the assumption that the theoretical distribution of TE is exponential, since the theoretical distribution does not always give good performance in reproducing TE data. For both, beta distribution is selected as the stochastic distribution to be used for the simulation. The mean yield and the distribution of the yield are simulated by the fitted distribution for different levels of parameters that are set by a few different scenarios.
For rainfall conditions, we set scenarios in that BMR days change by 5% and 10% in both directions, unfavorable (i.e., an increase in BMR days) and favorable (i.e., a decrease in BMR days). We adopt these levels of rainfall change referring to two contradicting rainfall predictions for East Africa: One foresees increases in precipitation within the range of 5% to 20% [7] , and the other anticipates drier conditions with an observation that recent rainfall is lower than the 1950-1979 averages by as much as 20% [9] . Twenty percent change in the mean value of daily rainfall corresponds to an about 10% change in the mean values of the number of BMR days in our data. For TE, we set scenarios in that its mean level is improved to 70% as a lower target and 80% as a higher target, because the past studies indicate that these target levels are practically attainable.
The mean yield will be simulated for each combination of the five levels of BMR days (baseline, 5% up/down, and 10% up/down) and the three levels of TE (baseline, 70% and 80%). The yield distribution will be simulated for four scenarios out of the 15 scenarios for the mean yield: first, baseline under the condition that all variables are kept constant at their sample means, second, the most unfavorable scenario in that BMR days increase by 10% with TE at the baseline level, third, BMR days increase by 10% with TE improved to 80%, and fourth, the most favorable one with 10% decrease in BMR days with TE improved to 80%. The output variable of the simulation model is yield (t·ha−1) in natural log form, which is reconverted to original values when necessary. The simulation is carried out using @risk 5.7 (Palisade Corp., Ithaca, NY).
2.3. Materials
The main dataset used for estimating the yield function in this paper was obtained from a nationwide survey of rice growing farmers conducted by the National Crops and Resources Research Institute (NaCRRI) in collaboration with the Africa Rice Centre. The original sample of farmers was drawn from all five major rice producing regions in Uganda by applying four-stage stratified random sampling as follows: 1) random selection of three rice growing districts in each sample region, 2) random selection of two rice growing sub-counties in each sample district, 3) random selection of two rice growing parishes in each sample sub-county, and 4) random selection of 20 rice growing farm households in each sample parish.
An interview survey was conducted from August to November 2009 using structured questionnaires that included questions on rice cultivation during the 2007 second season and the 2008 first season. Out of the whole sample, a subsample consisting of rainfed rice farmers was made, and then a sample for analysis (the sample hereafter) was made from this rainfed rice farmer subsample by discarding observations for which 1) the household characteristics are missing and 2) the rice yield is less than 25 kg·ha−1. The second criterion was adopted to exclude observations where the rice cultivation was total failure because of extreme factors beyond the farmers’ control, the inclusion of which caused non-convergence in the maximum-likelihood estimation. The sample obtained consists of 1028 rainfed farm plots planted with rice, either upland or lowland, cultivated by 799 farmers. The number of sample observations used for the analysis in this paper is presented by region and district in Table 1.
Rainfed rice is cultivated in two types of land: dryland and wetland. Commonly, the former is called upland and the latter lowland, the prime distinction between the two being the absence or presence of standing water in the fields when growing rice, respectively. The typical lowland is found in hydromorphic inland basins or inland valley bottoms, while typical upland is found on plateaus and sloping lands in inland valleys beyond the hydromorphic edge [5] . In this paper, we use the term “lowland” for wetland and the term “upland” for dryland, and examine the yield potentials of these land types separately.
All the data used in the estimation were obtained from the survey, except for rainfall, on which data were obtained from the Meteorological Center of Uganda. Beyond the total rainfall measured from 1 July 2007 to 30 June 2008, we use daily rainfall data during the year to prepare six monthly rainfall measures of the number of days with below minimum rainfall (BMR) by counting the number of days with rainfall less than 4 mm·day−1. For example, “BMR days: 1st month” is the average of days with rainfall less than 4 mm·day−1 in July 2007 (the 1st month of the 2007 second season) and January 2008 (the 1st month of the 2008 first season). The 4 mm·day−1 was selected as demarcating the “minimum” rainfall per day based on the recommendation that rainfed rice cultivation be practiced in areas where the 5-day total rainfall of 20 mm is assured for the period from sowing to 15 days before harvesting [18] .
3. Results and Discussion
3.1. Rainfed Rice Cultivation in Uganda
The extent of cultivation: rainfed rice cultivation is found throughout Uganda, except for the mountainous and pastoral areas in the eastern and southwestern corners of the country [19] . Our NaCRRI survey gives an estimate
Table 1. Sample distribution of rice farmers and rice plots and the percentage share of lowland and upland cultivation by region and district.
of 110,000 ha planted with rice in 2007-2008. Because the irrigated lowland area in the country is estimated to be 2000 ha [5] , rainfed rice takes more than 95% of the area planted with rice, even if two crops could be planted per year in all the irrigated area. For the sample, about 60% of rainfed rice cultivation was carried out on lowland and 40% on upland (Table 1). The distribution of upland and lowland in Uganda has a clear regional pattern: rainfed lowland cultivation dominates in eastern regions, and as one goes to the north and the west the percentage of rainfed upland cultivation increases.
Household characteristics of farmers cultivating rainfed rice: the household characteristics of rice farmers in the sample are summarized in Table 2. On average for the sample, rice farmers were around 40 years old, had reached the educational level of junior high school, had lived in their villages for more than 30 years, and had 8 family members, of whom 3 were children between 6 and 15 years old. Ten percent of them were female-headed households and crop cultivation was the main economic activity for more than 90% of rice farmers. Nearly 70% of farmers in the sample were small farmers with total cultivated area of less than 2 ha. These household characteristics are quite comparable to the characteristics of rice farmers reported by earlier studies conducted in various parts of Uganda [10] [20] -[22] .
When compared by land type, rice farmers cultivating rainfed lowland differed significantly from their counterparts cultivating rainfed upland for some characteristics. Lowland rice farmers were younger, had fewer female-headed households, had a greater share of their economic activities derived from crops, lived in their villages longer, and cultivated smaller farm land.
Actual rice yield and varieties planted: the first row of Table 3 gives the average rice yield per hectare for the sample, which was 1.9 t·ha−1, higher than the yield of 1.4 t·ha−1 reported in FAOSTAT for 2007 and 2008 [23] . The difference in the unit yield between lowland and upland was not so large, but the t-test indicates that the mean difference is significant (p = 0.003). The average yield distribution is skewed toward the high yield side, having a longer tail on the low yield side, with the median yield of 1.7 t·ha−1 for lowland and 1.6 t·ha−1 for upland.
The rice varieties planted by rainfed rice farmers are also shown in Table 3. The most popular variety was Supa for lowland and NERICA for upland, the former taking 50% of lowland rice planted area and the latter more than 70% of upland rice area. For lowland cultivation, Kaiso followed Supa. Reflecting differences in the share of lowland and upland by region, the diffusion of varieties had strong regional biases. It must be noted that all these varieties are “improved” or “modern” rice varieties. NERICA varieties were recently bred in Africa and Kaiso was brought to Uganda from China after the Green Revolution in Asia. Supa is said to be brought from Indonesia prior to the Green Revolution, but its high yielding records under experimental conditions suggest that
Table 2. Household characteristics of rice farmers in survey sample by land type, 2007-2008a.
a. SD = standard deviation. Mean difference between lowland and upland is significant at 1% level or higher if marked with * and not significant if marked with ns. b. Average of the values as assigned in the following categories: no formal education = 0, pre-primary = 1, primary = 2, junior = 3, ordinary level = 4, advanced level = 5, tertiary institution after O-level = 6, tertiary institution after A-level = 7, university = 8. c. Number of years living in the village of present domicile. d. Percentage of households headed by female. e. Percentage of households whose main economic activity is crop farming. f. Farmers cultivate less than 2 ha.
Table 3. Rice yield per hectare by land type and variety, 2007-2008a.
a. SD = standard deviation. The average yields followed by the same symbol are not statistically different at the 5% level of significance using Tukey’s test. b. The difference in average yield between lowland and upland is statistically significant (p-value = 0.003).
it is a variety of some improvements.
For the sample, in terms of average yields, the variety groups can be divided into three classes by Tukey’s test (Table 3): low-yield (Supa), middle-yield (NERICA) and high-yield (Kaiso and other lowland varieties). The average yield of other upland varieties was not statistically different from the yields of Supa or of NERICA. It is worth noting that some farmers planted NERICA on lowland, with an average yield that was significantly higher than the yield of NERICA planted to upland (p = 0.0001). On the other hand, very few farmers planted Supa on upland.
Production inputs in rainfed rice cultivation: the production inputs used by the rainfed rice farmers in the sample are summarized in Table 4. The average size of land area planted with rice, 0.6 ha farm−1, was quite uniform between the two land types. The non-land production inputs of seed, fertilizer, herbicide and labor are also shown in Table 4. For labor, the total labor used for weeding, for which reliable data were available, is shown. The intensities of most non-land inputs were at similar levels for lowland and upland, with the exception of fertilizer, for which the intensity was higher for upland than for lowland. It is also remarkable that farmers applying fertilizers and herbicides were still small minorities in Uganda.
Rainfall: the six rainfall measures, starting from the beginning of the two rainy seasons (July and January), are shown in Table 4, together with the total yearly rainfall from 1 July 2007 to 30 June 2008. Rainfall of 1000 mm per year, or 500 mm per season, is required for growing rice under rainfed conditions [19] . The seasons under study in 2007-2008 on average satisfied this condition for both lowland and upland. The distributions of BMR days were similar for both land types, though the mean values were significantly different, varying from 21 days to 27 days. It is critical for growing rice to have sufficient rainfall in the early growing stage, that is, the 1st and 2nd month of the two cropping seasons. The data shown in the table suggest that it was less likely, for both lowland and upland, that the condition of 5-day rainfall of 20 mm is satisfied for the early stage.
3.2. Frontier Yield Function
Estimated frontier yield functions: the results of stochastic frontier yield function estimation are summarized in Table 5 for the sample, and for the lowland and upland subsamples. In the estimation, the natural logarithm of the unit yield was regressed on the natural logarithm of non-land production inputs per hectare (Table 4) and on household characteristics (Table 2), variety dummies for “Supa” and “Kaiso and other lowland varieties” (Table 3), and the three measures of monthly rainfalls (Table 4). If there is zero value, a very small value, 0.001, was used instead of zero for log-transformation. As for the monthly rainfall measures, the first three months were included, which performed best in terms of the Akaike Information Criteria, in order to avoid multicollinearity. The total rainfall in the year 2007-2008 was also tested in the estimation, but it gave no significant coefficient. For other explanatory variables, only those that gave regression coefficients with the significance level of 10% or higher were retained. The frontier models assuming half-normal distribution were also estimated, but they were statistically inferior to the exponential models. In all the models shown in Table 5, all explanatory va
Table 4. Land area planted with rice, inputs per hectare in rice production, and rainfall by land type, 2007-2008a.
a. SD = standard deviation. Mean difference between lowland and upland is significant at the 1% level or higher if marked with * and not significant if marked with ns. b. Total labor input for weeding. 1 person-day = 8 hours. c. Below-minimum-rainfall days. d. The average number of days with rainfall less than 4 mm·day−1 in July 2007 and in January 2008. e. The average number of days with rainfall less than 4 mm·day−1 in August 2007 and in February 2008. f. The average number of days with rainfall less than 4 mm·day−1 in September 2007 and in March 2008. g. The average number of days with rainfall less than 4 mm·day−1 in October 2007 and in April 2008. h. The average number of days with rainfall less than 4 mm·day−1 in November 2007 and in May 2008. i. The average number of days with rainfall less than 4 mm·day−1 in December 2007 and in June 2008.
riables are treated as arguments of the yield function, as defined in Equation (1). We also estimated the technical inefficiency effects model, in which some variables, such as the household head’s age and educational level, affected the random term Ui, with inferior statistical performances.
First, let us turn to Regression [1] for the entire sample. Among the explanatory variables included in our trial regressions, 10 variables gave significant coefficients. The results are essentially consistent with the yield function estimated earlier using the data from the same survey [24] . Previous studies found the positive impacts of seeds on yield [10] [22] , and of fertilizers [22] [25] . Many studies found the negative impacts on the adoption of rainfed rice cultivation of farmers’ age [10] [20] [21] [26] . In studies where age is treated as a determinant of technical inefficiency, some found a negative impact [27] and some others a positive one [28] . Farmers with large family size have an advantage in labor intensive rice cultivation [28] . It is also a popular finding that there is a significant difference in rice yield between small and large farmers [22] .
The two variety dummies have positive impacts on yield, indicating that the yields of Supa, Kaiso, and other lowland varieties were on average higher than that of NERICA and other upland varieties. In particular, it is noteworthy that the yield performance of Supa was better than NERICA, contrary to the simple comparison in Table 2 without controlling rainfalls and other explanatory variables. The three monthly BMR days all gave
Table 5. Estimation results of stochastic frontier yield function for rainfed rice cultivation by land type, 2007-2008a.
a. The dependent variable is the logarithm of rice yield (kg·ha−1). The variables corresponding to blank cells and not shown in the table are those excluded from the models due to poor statistical performance. b. Upper-tail critical value at 10% of χ2 (1) is 2.706.
highly significant impacts on rice yield: negative impacts in the first two months and a positive impact in the third month. The negative impacts of these rainfall measures, which mean that a greater the number of days with rainfall of less than 4 mm·day−1 results in lower rice yields, suggest the importance of rain at the early stages of plant growth in rainfed rice cultivation. In particular, the large coefficient for the 1st month rainfall indicates that rainfall at the beginning of rice cultivation is critically important. Since rice generally requires sufficient water even in the third month (60 - 90 days) after planting, it would be reasonable that the coefficient of 3rd month BMR days be negative as well, contrary to our results. Given the fact that rainfall was most plentiful in the 3rd month in the seasons under study (Table 3), our results seem to indicate that higher solar radiation helped higher yield under a given level of rainfall.
Looking at regressions [2] and [3] , the positive impact of fertilizers on yield was found in lowland cultivation. Similarly, the family size mattered in lowland and the household head’s age did in upland. As to the variety dummies, regression [2] showed no yield difference among the variety groups for lowland, while regression [3] indicates that Supa, if planted in upland, yielded significantly less than NERICA and other upland varieties. Although there were such differences between the two regressions, the null hypothesis that there was no difference in the estimated coefficients between lowland and upland was accepted at the 10% significance level, indicating that there was no significant difference in the structure of rainfed rice technology between lowland and upland cultivation.
Technical efficiency: however, there was clear difference in the rainfed farmers’ TE between lowland and upland: The mean TE in lowland cultivation was 65%, which was significantly higher than the mean TE of 60% in upland cultivation at the 1% significance level. Such results could arise partly from the harsher and more vulnerable nature of upland, and partly from the fact that rainfed upland rice cultivation has a shorter history, with less experienced rice farmers than lowland rice cultivation.
Rice farmers’ TE in SSA reported in the recent literature have been found to be 51% - 53% in Northern Ghana [28] , 54% in Nigeria [26] and 68% - 70% in Mali [29] . A study obtained a rate of profit efficiency, consisting of TE and allocative efficiency, of around 50% for rice production in Uganda [30] . On the other hand, past studies in Asia have found mean TEs ranging from 74% to 94% for irrigated rice [31] -[34] and from 70% to 84% for rainfed rice [33] . Our TE estimates of 60% to 65% for rainfed rice farmers in Uganda are closer to the higher end of the TE range of SSA rice farmers, but consistently lower than the TEs of Asian rice farmers.
The average actual yields of farmers (Table 3) and the estimated TE levels together imply that the potential yield of rainfed rice cultivation in Uganda could be as high as around 3 t·ha−1 under the technology available at present in farmers’ fields. Such levels are comparable with those that farmers realize in advanced rainfed rice growing areas [10] [20] [22] [25] [35] . In order to realize this potential yield, the technical inefficiency must be reduced through various channels of technology extension. It was found for maize farmers in Ethiopia that efficient extension services could improve farmers’ TE to nearly 100% [36] .
3.3. Simulation Results
As our frontier yield function revealed, the unit yield of rainfed rice cultivation is significantly affected by rainfall conditions. How vulnerable is rainfed rice cultivation to changes in rainfall and to what extent can improvements in farmers’ TE counteract the changes? Table 6 summarizes the results of simulation for the mean yield.
If rainfall increased in the future as predicted by some studies [7] , there would be fewer problems. With a 10% decrease in BMR days, even with the present level of TE, the mean rice yield would be as high as 3 t·ha−1 for both the land types. A similar level of unit yield would be attained under the scenario of 5% decrease in BMR days, if farmers’ TE were improved to 80%. On the other hand, if the rainfall condition changed toward the unfavorable direction, the high yield potential of rainfed rice cultivation would be lost. In the scenario in that BMR days increase by 5%, the yield would decrease by nearly 30% from the baseline, and even if efforts were made to improve TE to 80%, the yield gain for both land types would not be enough to recover the yield loss due to the adverse climatic change. This exercise indicates that if climatic changes brought about less rainfall in the future and if rainfed rice cultivation were to achieve “revolutionary” levels, its tolerance to drought would have to be strengthened by all means through improvements in varieties and cultivation practices. In addition to analyzing the mean-level changes, let us see how the distribution of unit yield changes as rainfall and TE change. The stochastic distributions of yield generated are shown in Figure 1 for the four scenarios. The vertical line in the
Table 6. Simulated mean-yields under the baseline and alternative scenarios by land typea.
a. The figures in parentheses are percent change relative to the baseline yield. The baseline yield for each land type was obtained by inserting the mean values of the explanatory variables into the estimated frontier yield function and then converting them from log to original unit (t·ha−1), and therefore different from the average yields shown in Table 3, which are expressed as arithmetic means.
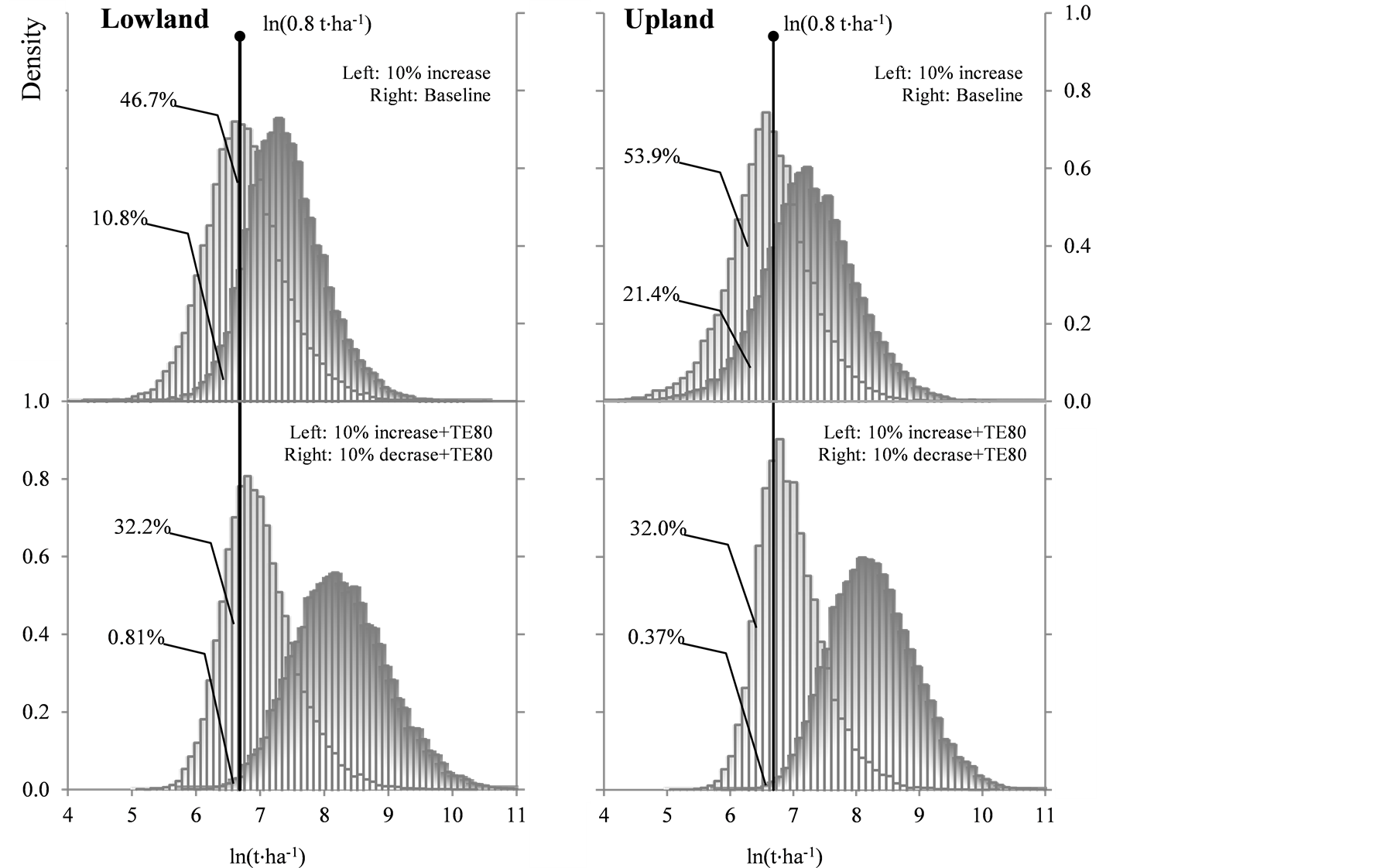
Figure 1.Distributions of simulated yield per hectare under the selected scenarios.
figure drawn at x = 6.68, which corresponds to 0.8 t·ha−1, is a break-even yield at which the value of output is equivalent to farmers’ paid-out costs. The unfavorable climatic change shifts the yield distribution toward left, resulting in an increase in the percentage of farmers below this break-even line from 11% to 47% for lowland and 21% to 54% for upland, if farmers’ TE were to remain at the present level. If TE were improved to 80%, however, the percentage would be less than one-third, which indicates that improving farmers’ TE is an effective measure for mitigating the adverse impact of unfavorable climatic changes and retaining rainfed rice farming viable and sustainable.
4. Conclusions
Using the data collected from a nationwide survey in Uganda, we have looked into the potential yield of rainfed rice cultivation by estimating the TE of rainfed rice farmers and how it is affected by climatic changes that bring changes in rainfall. The estimation of frontier yield function revealed that there was no difference in rice yield between rainfed lowland and rainfed upland, but the mean TE of lowland (65%) was higher than that of upland (60%). Given the technology available at present to farmers, the potential yield was estimated to be around 3 t·ha−1, which could be said to be “revolutionarily” high as the yield of rainfed rice cultivation [20] . However, rainfed rice cultivation is vulnerable to unfavorable climatic changes. Our simulation analyses revealed that a 10% to 20% decrease in rainfall in the early growth stages of rice cultivation could erase the “revolutionary” gains.
Improvements in farmers’ TE are important to extend a rice Green Revolution in East Africa where rice is a new, non-native crop. A shorter history of rice cultivation in the region is reflected in the consistently lower levels of rice farmers’ TE than in Asia. The need to increase human capacity through research and extension services is emphasized for an African Green Revolution to become a reality [37] . This is particularly true in the case of rice, since rice research in many East African countries is a very recent development, and therefore the talent pool of rice researchers and extension workers with good knowledge of rice technology is still underdeveloped. To make rainfed rice cultivation viable, sustainable and revolutionary, it is no doubt necessary to improve farmers’ TE through designing and promoting effective technology extension services, backed up by systematic and persistent research on rice cultivation, including the research to strengthen drought tolerance through improvements in varieties and cultivation practices.
Acknowledgements
The data used in this study were collected by NaCRRI in collaboration with the Africa Rice Center. This study was also partially supported by the JSPS Science Research Fund (KAKENHI No.19405046 and 22780201). We also thank Dr. Akio Goto for providing us with Uganda rainfall data. Views and opinions expressed in this paper are solely those of the authors, not necessarily of the institutions to which they belong.
References
- Otsuka, K. and Kalirajan, K. (2006) Rice Green Revolution in Asia and Its Transferability to Arica: An Introduction. The Developing Economies, 44, 107-122. http://dx.doi.org/10.1111/j.1746-1049.2006.00009.x
- Somado, E.A., Guei, R.G. and Keya, S.O. (2008) NERICA: The New Rice for Africa—A Compendium. Africa Rice Center, Cotonou, 1-195.
- Larson, D.F., Otsuka, K., Kajisa, K., Estudillo, J. and Diagne, A. (2010) Can Africa Replicate Asia’s Green Revolution in Rice? Policy Research Working Paper 5478. World Bank, Washington DC.
- Barker, R. and Herdt, R.W. (1985) The Rice Economy of Asia. Resources for the Future, Washington DC.
- Balasubramanian, V., Sie, M., Hijmans, R.J. and Otsuka, K. (2007) Increasing Rice Production in Sub-Saharan Africa: Challenges and Opportunities. Advances in Agronomy, 94, 55-133. http://dx.doi.org/10.1016/S0065-2113(06)94002-4
- Fujiie, H., Maruyama, A., Fujiie, M., Takagaki, M., Merrey, D.J. and Kikuchi, M. (2011) Why Invest in Minor Projects in Sub-Saharan Africa? An Exploration of the Scale Economy and Diseconomy of Irrigation Projects. Irrigation and Drainage Systems, 25, 39-60. http://dx.doi.org/10.1007/s10795-011-9111-4
- IPCC (2001) Climate Change 2001: The Scientific Basis. Cambridge University Press, Cambridge, 61-77.
- Challinor, A., Wheeler, T., Garforth, C., Craufurd, P. and Kassam, A. (2007) Assessing the Vulnerability of Food Crop Systems in Africa to Climate Change. Climatic Change, 83, 381-399. http://dx.doi.org/10.1007/s10584-007-9249-0
- Williams, A.P. and Funk, C. (2011) A Westward Extension of the Warm Pool Leads to a Westward Extension of the Walker Circulation, Drying Eastern Africa. Climate Dynamics, 37, 2417-2435. http://dx.doi.org/10.1007/s00382-010-0984-y
- Kijima, Y., Sserunkuuma, D. and Otsuka, K. (2006) How Revolutionary Is the “NERICA Revolution”? Evidence from Uganda. The Developing Economies, 44, 252-267. http://dx.doi.org/10.1111/j.1746-1049.2006.00016.x
- Nakano, Y., Bamba, I., Diagne, A., Otsuka, K. and Kajisa, K. (2011) The Possibility of a Rice Green Revolution in Large-Scale Irrigation Schemes in Sub-Saharan Africa, World Bank Working Paper 5560. World Bank, Washington DC.
- World Bank (2007) Africa Region: Irrigation Business Plan. World Bank Africa Region, Washington DC, 1-98.
- Farrell, M.J. (1957) The Measurement of Productive Efficiency. Journal of the Royal Statistical Society: Series A, 120, 253-281. http://dx.doi.org/10.2307/2343100
- Coelli, T.J., Rao, D.S.P. and Battese, G.E. (2000) An Introduction to Efficiency and Productivity Analysis. Kluwer Academic Publishers, Norwell, 1-275.
- Aigner, D., Lovell, C.A.K. and Schmidt, P. (1977) Formulation and Estimation of Stochastic Frontier Function Models. Journal of Econometrics, 6, 21-37. http://dx.doi.org/10.1016/0304-4076(77)90052-5
- Battese, G.E. and Coelli, T.J. (1995) A Model for Technical Inefficiency Effects in a Stochastic Frontier Production for Panel Data. Empirical Economics, 20, 325-332. http://dx.doi.org/10.1007/BF01205442
- Jondrow, J., Lovell, C.A.K., Materov, I.S. and Schmidt, P. (1982) On the Estimation of Technical Inefficiency in the Stochastic Frontier Production Function Model. Journal of Econometrics, 19, 232-238. http://dx.doi.org/10.1016/0304-4076(82)90004-5
- NaCRRI (2010) Rice Cultivation Handbook. NERICA Promotion Project. NaCRRI, Namulonge, 7-8.
- Haneishi, Y., Okello, S.E., Asea, G., Tsuboi, T., Maruyama, A., Takagaki, M. and Kikuchi, M. (2013) Exploration of Rainfed Rice Farming in Uganda Based on a Nationwide Survey: Evolution, Regionality, Farmers and Land. African Journal of Agricultural Research, 8, 3318-3329.
- Kijima, Y., Otsuka, K. and Sserunkuuma, D. (2011) An Inquiry into Constraints on a Green Revolution in Sub-Saharan Africa: The Case of NERICA Rice in Uganda. World Development, 39, 77-86. http://dx.doi.org/10.1016/j.worlddev.2010.06.010
- Fujiie, H., Maruyama, A., Fujiie, M., Takagaki, M. and Kikuchi M. (2010) Determinants of NERICA Adoption in Uganda Based on Duration Analysis. Tropical Agriculture and Development, 54, 17-24.
- Miyamoto, K., Maruyama, A., Haneishi, Y., Matsumoto, S., Tsuboi, T., Asea, G., Okello, S.E., Takagaki, M. and Kikuchi, M. (2012) NERICA Cultivation and Its Yield Determinants: The Case of Upland Rice Farmers in Namulonge, Central Uganda. Journal of Agricultural Science, 4, 120-135.
- FAO (2013) FAOSTAT. http://faostat.fao.org/site/291/default.aspx
- Haneishi, Y., Maruyama, A., Asea, G., Okello, S.E., Tsuboi, T., Takagaki, M. and Kikuchi, M. (2013) Exploration of Rainfed Rice Farming in Uganda Based on a Nationwide Survey: Regionality, Varieties and Yield. African Journal of Agricultural Research, 8, 4038-4048.
- Kijima, Y., Otsuka, K. and Sserunkuuma, D. (2008) Assessing the Impact of NERICA on Income and Poverty in Central and Western Uganda. Agricultural Economics, 38, 327-337. http://dx.doi.org/10.1111/j.1574-0862.2008.00303.x
- Umeh, J.C. and Ataborh, E.M. (2007) Efficiency of Rice Farmers in Nigeria: Potentials for Food Security and Poverty Alleviation. Proceedings of 16th International Farm Management Congress, Cork, 15-20 July 2007, 613-625.
- Tiamiyu, S.A., Akintola, J.O. and Rahji, M.A.Y. (2010) Production Efficiency among Growers of New Rice for Africa in the Savanna Zone of Nigeria. Agricultura Tropica et Subtropica, 43,134-139.
- Al-Hassan, S. (2008) Technical Efficiency of Rice Farmers in Northern Ghana. AERC Research Paper 178. African Economic Research Consortium.
- Audibert, M. (1997) Technical Inefficiency Effects among Paddy Farmers in the Villages of the “Office Du Niger”, Mali, West Africa. Journal of Productivity Analysis, 8, 379-394. http://dx.doi.org/10.1023/A:1007767508848
- Hyuha, T.S., Bashaasha, B., Nkonya, E. and Kraybill, D. (2007) Analysis of Profit Inefficiency in Rice Production in Eastern and Northern Uganda. African Crop Science Journal, 15, 243-253.
- Tadesse, B. and Krishnamoorthy, S. (1997) Technical Efficiency in Paddy Farms of Tamil Nadu: an Analysis Based on Farm Size and Ecological Zone. Agricultural Economics, 16, 185-192. http://dx.doi.org/10.1016/S0169-5150(97)00004-2
- Xu, X. and Jeffrey, S.R. (1998) Efficiency and Technical Progress in Traditional and Modern Agriculture: Evidence from Rice Production in China. Agricultural Economics, 18, 157-165. http://dx.doi.org/10.1016/S0169-5150(97)00050-9
- Mariano, M.J., Villano, R. and Fleming, E. (2010) Are Irrigated Farming Ecosystems More Productive than Rainfed Farming Systems in Rice Production in the Philippines? Agriculture, Ecosystems and Environment, 139, 603-610. http://dx.doi.org/10.1016/j.agee.2010.10.004
- Tan, S., Heerink, N., Kuyvenhoven, A. and Qu, F. (2010) Impact of Land Fragmentation on Rice Producers’ Technical Efficiency in South-East China. NJAS-Wageningen Journal of Life Sciences, 57, 117-123. http://dx.doi.org/10.1016/j.njas.2010.02.001
- Lamo, J., Imanywoha, J., Bigirwa, G., Walusimbi, M., Kyetere, D., Kikafunda, J. and Kalule, T. (2010) First NERICA Rice Released in Uganda Tops Farmers’ Rankings. International Rice Research Notes, 35, 1-4.
- Seyoum, E.T., Battese, G.E. and Fleming, E.M. (1998) Technical Efficiency and Productivity of Maize Producers in Eastern Ethiopia: A Study of Farmers within and Outside the Sasakawa-Global 2000 Project. Agricultural Economics, 19, 341-348. http://dx.doi.org/10.1016/S0169-5150(98)00037-1
- Ejeta, G. (2010) African Green Revolution Needn’t Be a Mirage. Science, 327, 831-832. http://dx.doi.org/10.1126/science.1187152


