Agricultural Sciences
 Vol.3 No.2(2012), Article ID:18385,7 pages DOI:10.4236/as.2012.32025

An empiric equation for the latent heat of vaporization of moisture in bananas during its isothermal drying

Wilton Pereira da Silva*, Cleide Maria Diniz Pereira da Silva e Silva, Fernando José de Almeida Gama, Josivanda Palmeira Gomes

Federal University of Campina Grande, Campina Grande, Brazil; *Corresponding Author: wiltonps@uol.com.br

Received 16 December 2011; revised 25 January 2012; accepted 9 February 2012

Keywords: Energy; agricultural products; dried banana; heat and mass transfer

ABSTRACT

In order to determine the energy needed to artificially dry a product, the latent heat of vaporization of moisture in the product, hfg, must be known. Generally, the expressions for hfg reported in the literature are of the form hfg = h(T)f(M), where h(T) is the latent heat of vaporization of free water, and f(M) is a function of the equilibrium moisture content, M. But expressions of this type contain a simplification because, in this case, the ratio hfg/h would only depend to the moisture content. In this article a more general expression for the latent heat of vaporization, namely hfg = g(M,T), is used to determine hfg for banana. To this end, a computer program was developed which fits automatically about 500 functions, with one or two independent variables, imbedded in its library to experimental data. The program uses nonlinear regression, and classifies the best functions according to the least reduced chi-square. A set of executed statistical tests shows that the generalized expression used in this work given by hfg = g(M,T) produces better results of hfg for bananas than other equations found in the literature.

1. INTRODUCTION

One of the important stages in several productive processes, in the most different areas of human activity, is that regarding the drying of bodies or products constituted by porous materials. As example, drying is used in the following fields: foodstuff, ceramics, pharmaceutical and paper industries. The drying of a wet body can happen in a natural or artificial way. In the case of artificial drying, the most common method for agricultural products is to heat up the air, decreasing its relative humidity, and soon after to transfer it, in a given velocity, for the ambient in which it is placed in contact with such product. Then, there is a continuous process of transfer of heat from air to inside the body. Simultaneously, there is transfer of moisture from the interior of the body to its surface, and from the surface to the drying air, in the form of vapor.

In several studies on artificial drying of a product, it is observed that the determination of the amount of energy requested in the process depends, among several factors, on the latent heat of vaporization, hfg, of water in the product. In addition, in the determination of the apparent thermal diffusivity to describe the heat transfer from air to inside the product, hfg is required [1-11]. In some works, latent heat of vaporization is neglected to describe heat transfer from air to inside product during the drying process [12]. In several works, when researchers do not know hfg in given drying condition, they use latent heat of vaporization of free water, h [1,4,7,10]. But hfg in general is significantly different of the latent heat of vaporization h of free water, and it is dependent on the studied product. So, many researchers have conducted studies with objective of determining expressions for the calculation of hfg for several products during the drying. Brook and Foster [13], cited by Brooker et al. [14], determined expressions for the calculation of hfg for several products, using experimental data, presupposing that the relation hfg/h for a given product could be written through a function which depends only of the moisture content of the product.

The expression proposed by Brook and Foster [13] is used in works about drying simulations of agricultural products as, for example, in References [15,16]. Al-Mahasneh et al. [17] studied moisture sorption thermodynamics of defatted sesame meal and they found good result admitting that the ratio hfg/h depends only on moisture content. Prado and Sartori [18] also used the general expression proposed by Brook and Foster [13] to study simultaneous heat and mass transfer in packed bed drying of seeds having a mucilage coating. Corrêa et al. [19] modified the function hfg/h proposed by Brook and Foster [13], and they fitted the modified function to the data obtained for corn. Kaleemullah and Kailappan [20] determined an expression for the calculation of hfg for red chillies using experimental data obtained for this product. In these works aforementioned, the dependence of the ratio hfg/h with the temperature of the product was not considered.

The objective of this article is to investigate the dependence of the ratio hfg/h with the temperature of the drying air for a given product, and to verify if that dependence is significant in the determination of an expression for hfg. In addition, it was studied a way of including such dependence in the determination of an empiric expression for the calculation of hfg for bananas. In this study, the obtained expression was compared with other available ones in the literature.

2. MATERIAL AND METHODS

In order to obtain an expression for the calculation of the latent heat of vaporization, hfg, of the water in a product, usually the Clausius-Clapeyron’s equation is used (see, for example, Smith et al. [21]), supposing that the ideal gas equation can be applied to the vapor, being neglected the volume of water in the liquid phase. A usual procedure in the solution of the Clausius-Clapeyron’s equation consists in the integration of this equation considering hfg as a constant value between two given states. For free water, the latent heat of vaporization, h, is obtained with the same previous procedure, being substituted the partial pressure of water vapor, Pv, by the partial pressure of water vapor at saturation, Pvs. In this way, observing that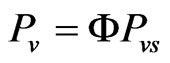, where 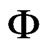is the relative humidity of the air, and comparing the expression obtained for hfg with the expression obtained for h, both in the same temperature band, we write (see, for example, Brooker et al. [14]):

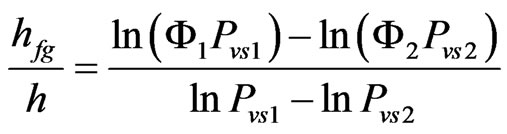. (1)

If and Pvs are determined for the states 1 and 2, the ratio hfg/h, given by Eq.1, is known. In this paper, the relative humidity of the air, 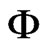, will be determined by interpolation of the Modified-Oswin equation fitted to the experimental data of banana, and it was made by [2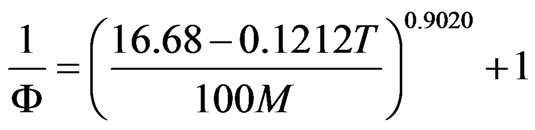2]:

(2)

where T is the temperature (˚C), is the relative humidity of the air (decimal) and M is the equilibrium moisture content (decimal, dry basis). Given M and T, the relative humidity of the air, , can be determined from Eq.2.

The partial pressure of water vapor at saturation can be determined from, for example, experimental data available in Brooker et al. [14], or in Smith et al. [21]. These data could be used in the fit, for example, of Antoine’s equation. However, the expression for Pvs was obtained using Riedel’s equation [23,24], because that equation presents better indicators of fit than Antoine’s equation. In this paper, the parameters of Riedel’s equation were obtained through non-linear regression using the available data in Brooker et al. [14], between 0 and 85˚C. Thus, using LAB Fit Curve Fitting Software V. 7.2.48 (www.labfit.net), the obtained equation for Pvs is given by the following way:

, (3)

where Pvs is obtained in kPa when T is given in ˚C. For the mentioned fit, it was obtained the determination coefficient 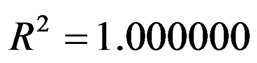and reduced chi-square (almost perfect fit). The form of Eq.3 results of the integration of Clausius-Clapeyron’s equation combined with the ideal gas equation applied to the vapor and the supposition that the latent heat of vaporization of free water is linear function of the temperature.

With Eqs.2 and 3, and Pvs can be determined for specified values of M and T, and it makes possible to determine the ratio hfg/h through Eq.1. On the other hand, an expression for the latent heat of vaporization of free water is given by [1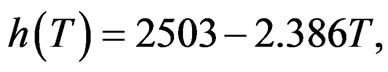4]:

(4)

where h is obtained in kJ·kg–1 when the temperature is given in ˚C.

In works about determination of latent heat of vaporization of water in a given product, it is common to admit that the ratio hfg/h, in a given temperature interval, only depends on the moisture content of the product. Brook and Foster [13] proposed the following equation:

, (5)

where the parameters A and B are determined by curve fitting. Corrêa et al. [19] proposed a modification in Eq.5:

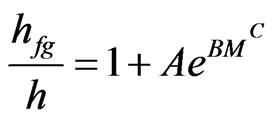. (6)

Having Eq.4, and knowing the parameters of Eqs.5 and 6, the last two equations can be rewritten to calculate latent heat of vaporization of water in a product of the following way:

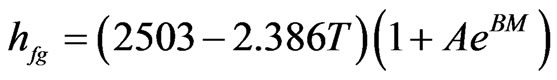(7)

and

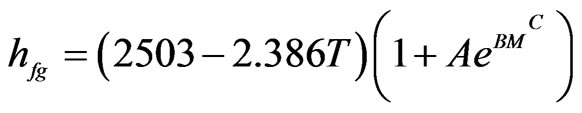. (8)

Obviously, in Eqs.7 and 8 it is supposed that the latent heat of vaporization of water in the product is given by a function expressed by two other, with separation of variables, in the form:

. (9)

In this paper, it was investigated if a more general function, without the previous supposition of separation of variables, given in the form expressed by Eq.10, describes the latent heat of vaporization of water in a product better than Eq.9:

(10)

The procedure used in the investigation for bananas involved five levels for the equilibrium moisture content, M (0.10; 0.15; 0.20; 0.25 and 0.30 db), and four levels for the temperature, T (10˚C; 20˚C; 30˚C and 40˚C). The calculation of the ratio hfg/h through Eq.1, for a given equilibrium moisture content, M, in a specified temperature, T, presupposes the knowledge of the relative humidity of the air, 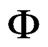, in two states, named 1 and 2. Thus, the relative humidity of the air was calculated, through Eq.2, in a state 1, with T1 = T + 1˚C, and in a state 2, with T2 = T − 1˚C. The two states around T could be characterized by other values, as 0.5˚C, for example, instead 1˚C. However, the chosen band, defined by 1˚C, produces the same results that the band defined by 0.5˚C and, then, the first band was used in the calculations. The partial pressure of vapor at saturation was calculated through Eq.3 and this makes it possible to calculate the ratio hfg/h using Eq.1. Then, the value of hfg could be determined for each M and T, since h(T) can be calculated by the Eq.4. Thus, through curve fit, the parameters A and B of Eq.7 could be determined, or the parameters A, B and C of Eq.8. The analysis of the results for the points (M, T, hfg/h) could indicate if the consideration of constant value for c/h, with respect to the temperature, is correct or not. If such consideration is not correct, the determination of another expression can be tried for hfg, proposing a more general function of M and T. For such, the “Finder” option of LAB Fit® software was used. This option fits, in an automatic way, about 500 compact functions of one and two independent variables contained at its library to the experimental data. This tool was developed by first two authors of this paper and it was incorporated to LAB Fit® since version 7.2.18. The main characteristic of “Finder” is to determine empiric equations seeking to the description of experimental data. “Finder” classifies the best fitted functions through least reduced chi-square. When the expression for hfg is determined through “Finder”, a comparison between this expression and those expressions obtained by fittings of Eqs.7 and 8 will be made. Such comparison will be accomplished with base in the following statistical tests: coefficient of determination, reduced chi-square and tStudent test.

3. RESULTS AND DISCUSSION

For the specified values for temperature and equilibrium moisture content in the banana, Table 1 could be set up, which indicates the relative humidity of the air, , calculated through Eq.2.

On the other hand, using the Eq.3, the partial pressure of water vapor at saturation could be determined, in the neighborhoods of each specified temperature: Pvs1 (T1 = T + 1˚C) and Pvs2 (T2 = T − 1˚C). The results are shown in Table 2.

With the results obtained in Tables 1 and 2, Eq.1 can be used for determination of the ratio hfg/h for the values of the temperature and moisture content previously specified, and it resulted in Table 3.

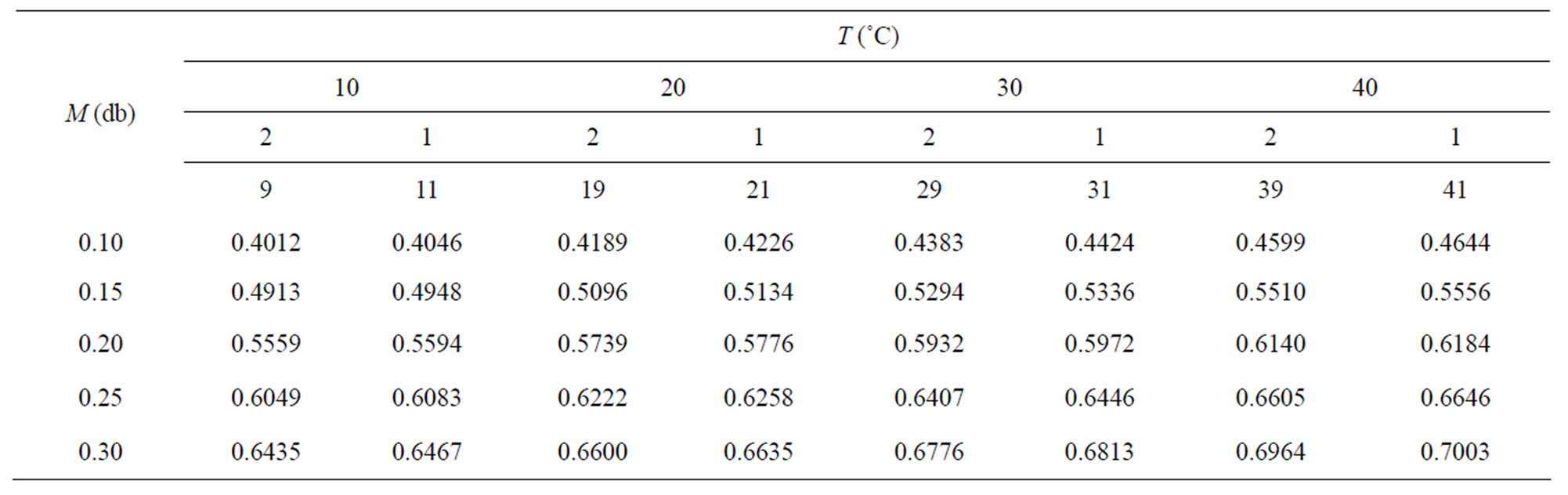
Table 1. Relative humidity of the air, Φ, obtained through Eq.2 for banana, in the neighborhoods of the established temperatures.

Table 2. Partial pressure of water vapor at saturation obtained through Eq.3, in the neighborhoods of the established temperatures.

Table 3. Ratio hfg/h calculated through Eq.1 for banana.

An observation of Table 3 indicates that the dependence among hfg/h and the temperature exists for given moisture content. For moisture content equal to 0.10, for example, the percentile discrepancy of hfg/h between 10 e 40˚C is of, approximately, 2.65%. Then, it is evident the introduction of a systematic error when such ratio is described by Eq.5 or 6. This can be visualized by the fitting, for example, of Eq.5 to the data of Table 3, as shown in Figure 1. Figure 1 shows that all the points involving the temperatures 30˚C and 40˚C are located above of fitted surface while the points involving the temperatures 10˚C and 20˚C are below.

On the other hand, the latent heat of vaporization of free water can be obtained through Eq.4, and it is shown in Table 4.

Once obtained the values of the ratio hfg/h (Table 3) and h (Table 4), the latent heat of vaporization of moisture in the banana, hfg, can be obtained by multiplication of the two values, and it is shown in Table 5.

An observation of Table 5 makes it possible to say: the bigger the equilibrium moisture content of banana is, the more hfg approximates the value of h. On the other hand, comparing the data of Table 4 with the data of Table 5, it can be noticed that a considerable error is made when substituting h for hfg. The smallest error between hfg and h is 3.6% (T = 10˚C; M = 0.30), and the bigger is 8.4% (T = 40˚C; M = 0.10).

The fit of Eq.7 to the data of Table 5 gives the expression:

(11)

with hfg in kJ·kg−1; T in ˚C and M decimal. Eq.11 involves four parameters, although two have only been

Figure 1. Eq.5 fitted to data of Table 3. The full circles represent experimental points above or on the surface, and the empty circles below it. Each vertical line gives an idea of the distance between the experimental point and the surface.

Table 4. Latent heat of vaporization for free water, h, obtained by Eq.4.

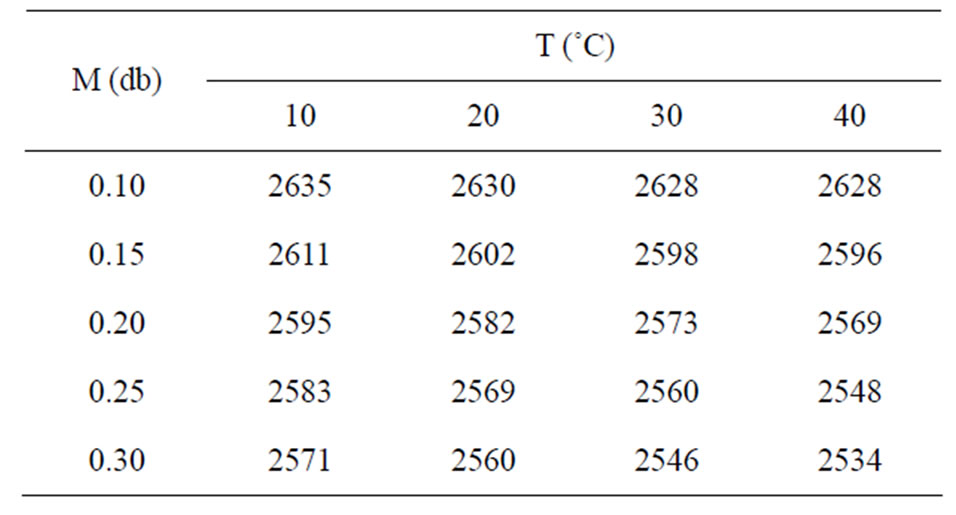
Table 5. Latent heat of vaporization of moisture in banana, hfg, (kJ·kg−1).

determined by curve fitting in the present paper. About the fit, the following results are presented for the accomplished statistical tests. With respect to the reduced chi-square, it was obtained. For the coefficient of determination, it was obtained R2 = 0.756869. For t-Student test, it was obtained P(t) = 0 for two determined parameters. Details on these statistical tests can be obtained, for example, in Bevington and Robinson [25] or in Taylor [26]. A plot for the function hfg = (M,T), given by Eq.11, is presented in Figure 2.

For Eq.8 fitted to the data of Table 5, it was obtained:

(12)

with hfg in kJ·kg−1, T in ˚C and M decimal. Eq.12 involves five parameters, although three have only been

Figure 2. Plot of hfg(M,T) obtained by the proposed model through Eq.11. The full circles represent experimental points above or on the surface, and the empty circles below it. Each vertical line gives an idea of the distance between the experimental point and the surface.

determined by curve fitting in the present paper. With respect to the statistical tests, it was obtained R2 = 0.760549 and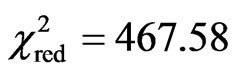. The t-Student test for the first parameter indicates that the probability that this parameter is zero is 74.8%. The second parameter has a probability equal to 19.0%, and the third, 71.2%. The plot of the function hfg (M,T), given by Eq.12, is shown in Figure 3.

From statistical indicators 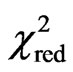and R2 we can’t conclude that Eq.12 is better than Eq.11 to describe data of Table 5. In addition, three parameters of Eq.12, determined by curve fitting, have a considerable probability of being zero, in spite of the obtained values. This means that the model given by Eq.12 should be rejected as expression for the calculation of the latent heat of vaporization of water in banana. On the other hand, the fit which resulted in Eq.11 has very bad statistical indicators, and this equation should also be rejected as expression for the calculation of latent heat of vaporization of water in banana.

As the inspection of Table 3 indicates a considerable dependence between the ratio hfg/h and the temperature, functions of the type suggested by Brook and Foster [13], given by Eq.9, with separation of variables, cannot be the more adapted to express the latent heat of vaporization of water in banana.

Using LAB Fit®’s Finder for the data of Table 5, the software related the best functions among the existent ones in its library. The one that best represents the data of Table 5 is the function identified by the order number given by 450:

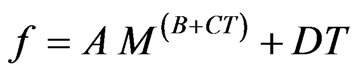. (13)

where A, B, C, and D are the parameters of the fit.

After fit of this function to the data, it was obtained:

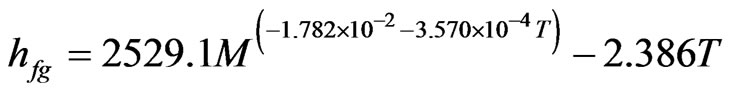(14)

where hfg is obtained in kJ·kg−1 when M is decimal and T is given in ˚C. Eq.14 involves four parameters, all them determined by curve fitting in this paper. Statistical indicators to the nonlinear regression of this function were obtained as it follows: R2 = 0.996725 and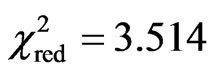. In this fit, all the parameters are significant because, for all them, t-Student test is zero: P(t) = 0. The indicators of the quality of this last fit are much better than those referring ones to Eqs.11 and 12 and, for this reason, Eq.14 can be considered as an option for the determination of latent heat of vaporization of water in banana. The plot of hfg (M,T), given by Eq.14, is presented in Figure 4.

The idea of the precision of a result obtained by Eq.14, in comparison to the corresponding value in Table 5, can be given performing the calculation of hfg with M = 0.10 and T = 20˚C, for example. For such values of M and T, it is determined 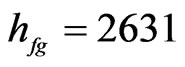kJ·kg−1 (Eq.14) and kJ·kg−11 (Table 5), and this means that the two values have a percentile discrepancy of only 0.04%.

Naturally, the more precise the results obtained by Eq.2 for are, the better will be the results obtained by Eq.14 for hfg.

For the determination of the uncertainty of a value obtained through fitted function, the covariance matrix must be known, and this matrix also is given by LAB Fit® software (see Eq.15).

With the covariance matrix known, the uncertainty of a value calculated by Eq.14 is determined by error propagation [27]:

, (16)

where f is given by Eq.13, n is the number of fitted parameters, and cov(zj,zk) is the covariance between the parameters zj and zk. In Eq.15, the element (1,1) is cov(A,A), the element (1,2) is cov(A,B), and so on. Then, performing the calculation of hfg again, with M = 0.10

(15)

Figure 3. Plot of hfg(M,T) obtained by the proposed model through Eq.12. The full circles represent experimental points above or on the surface, and the empty circles below it. Each vertical line gives an idea of the distance between the experimental point and the surface.

Figure 4. Plot of hfg(M,T) obtained by the proposed model through Eq.14. The full circles represent experimental points above or on the surface, and the empty circles below it.

and T = 20˚C, the complete result obtained by Eq.14, including uncertainty calculated by error propagation, is:

(17)

with a probability of 95.4%.

4. CONCLUSIONS

The analysis of the obtained results for banana, in the temperature band of 10˚C up to 40˚C and moisture content between 0.10 and 0.30 (db) makes it possible to affirm:

1) As the ratio hfg/h depends on the temperature, for given moisture content, functions of the type of Eq.10 are more suitable than those given by Eq.9 for the determination, by curve fitting, of an empiric expression for the latent heat of vaporization of water in banana.

2) For banana in drying process, the latent heat of vaporization hfg decreases with the increase of the moisture content and the increase of the temperature.

3) The statistical indicators of the fit which resulted in Eq.13 suggest that such equation is a good option for the determination of the latent heat of vaporization of the analyzed product.

4) The obtained results for banana suggest that the proposed methodology in this paper can constitute in a good alternative for the determination of empiric expressions for the latent heat of vaporization of water in another products.

REFERENCES

  1. Liu, J.Y. and Cheng, S. (1991) Solutions of Luikov equations of heat and mass transfer in capillary-porous bodies. International Journal of Heat and Mass Transfer, 34, 1747-1754. doi:10.1016/0017-9310(91)90150-D
  2. Kiranoudis, C.T., Maroulis, Z.B. and Marinos-Kouris, D. (1995) Heat and mass transfer model building in drying with multiresponse data. International Journal of Heat and Mass Transfer, 38, 463-480. doi:10.1016/0017-9310(94)00166-S
  3. Wang, N., Brennan and J.G. (1995) A mathematical model of simultaneous heat and moisture transfer during drying of potato. Journal of Food Engineering, 24, 47-60. doi:10.1016/0260-8774(94)P1607-Y
  4. Wang, Z.H. and Chen, G. (2000) Heat and mass transfer in batch fluidized-bed drying of porous particles. Chemical Engineering Science, 55, 1857-1869. doi:10.1016/S0009-2509(99)00446-7
  5. Chemkhi, S., Zagrouba, F. and Bellagi, A. (2005) Modelling and simulation of drying phenomena with rheological behaviour. Brazilian Journal of Chemical Engineering, 22, 153-163. doi:10.1590/S0104-66322005000200001
  6. Sfredo, M.A., Finzer, J.R.D. and Limaverde, J.R. (2005) Heat and mass transfer in coffee fruits drying. Journal of Food Engineering, 70, 15-25. doi:10.1016/j.jfoodeng.2004.09.008
  7. Nascimento, J.J.S., Lima, A.G.B., Teruel, Bárbara, J. and Belo, F.A. (2006) Transmisión de calor y materia con reducción de volumen durante el secado de ladrillos de cerámica. Información Tecnológica, 17, 125-132. doi:10.1016/j.jfoodeng.2005.09.010
  8. Trujillo, F.J., Wiangkaew, C. and Pham, Q.T. (2007) Drying modeling and water diffusivity in beef meat. Journal of Food Engineering, 78, 74-85.
  9. Suvarnakuta, P., Devahastin, S. and Mujumdar, A.S. (2007) A mathematical model for low-pressure superheated steam drying of a biomaterial. Chemical Engineering and Processing, 46, 675-683. doi:10.1016/j.cep.2006.09.002
  10. Mariani, V.C., Lima, A.G.B. and Coelho, L.S. (2008) Apparent thermal diffusivity estimation of the banana during drying using inverse method. Journal of Food Engineering, 85, 569-579. doi:10.1016/j.jfoodeng.2007.08.018
  11. Meeso, N., Nathakaranakule, A. and Madhiyanon, T., Soponronnarit, S. (2008) Different strategies of far-infrared radiation application in Paddy drying. International Journal of Food Engineering, 4, 1267. doi:10.1016/j.biosystemseng.2003.09.004
  12. Wu, B., Yang, W. and Jia, C. (2004) A three-dimensional numerical simulation of transient heat and mass transfer inside a single rice kernel during the drying process. Biosystems Engineering, 87, 191-200.
  13. Brook, R.C. and Foster, G.H. (1981) Drying, cleaning and conditioning. In: CRC Handbook of Transportation, Marketing and Agriculture, v.2, CRC Press, Boca Raton.
  14. Brooker, D.B., Bakker-Arkema, F.W. and Hall, C.W. (1992) Drying and storage of grains and oilseeds. The AVI Publishing Company, Westport.
  15. Mata, M.E.R.M.C., Dantas, L.A. and Braga, M.E.D. (1999) Programa computacional para simulação de secagem de grãos. Revista Brasileira de Produtos Agroindustriais, Campina Grande, 1, 33-50.
  16. Cavalcanti Mata, M.E.R.M. and Duarte, M.E.M. (2003) Drying simulation theory of the cowpea considering the grains shrinkage. Revista Brasileira de Produtos Agroindustriais, Campina Grande, 5, 179-185.
  17. Al-Mahasneh, M.A., Rababah, T.M. and Yang, W. (2007) Moisture sorption thermodynamics of defatted sesame meal (DSM). Journal of Food Engineering, 81, 735-740. doi:10.1016/j.jfoodeng.2007.01.010
  18. Prado, M.M. and Sartori, D.J.M. (2008) Simultaneous heat and mass transfer in packed bed drying of seeds having a mucilage coating. Brazilian Journal of Chemical Engineering, 25, 39-50. doi:10.1590/S0104-66322008000100006
  19. Corrêa, P.C., Christ, D., Martins, J.H. and Mantovani, B.H.M. (1998) Curvas de dessorção e calor latente de vaporização para as sementes de milho pipoca. Revista Brasileira de Engenharia Agrícola e Ambiental, 2, 75-79.
  20. Kaleemullah, S. and Kailappan, R. (2005) Latent heat of vaporization of moisture from red chillies. International Journal of Food Properties, 8, 199-205. doi:10.1081/JFP-200060232
  21. Smith, J.M., Van Ness, H.C. and Abbot, M.B. (2004) Introduction to chemical engineering thermodynamics. Mcgraw-Hill, New York.
  22. Phoungchandang, S. and Woods, J.L. (2000) Moisture diffusion and desorption isotherms for banana. Food Engineering and Physical Properties, 65, 651-657.
  23. Athié, I., Castro, M.F.P.M., Gomes, R.A.R. and Valentini, S.R.T. (1998) Conservação de Grãos. Fundação Cargill, Campinas.
  24. Shore, H., Brauner, N. and Shacham, M. (2002) Modeling Physical and thermodynamic properties via inverse normalizing transformation. Industrial & Engineering Chemistry Research, 41, 651-656. doi:10.1021/ie010039s
  25. Bevington, P.R. and Robinson, D.K. (1992) Data reduction and error analysis for the physical sciences. 2nd Edition, WCB/McGraw-Hill, Boston.
  26. Taylor, J.R. (1997) An introduction to error analysis. 2nd Edition, University Science Books, Sausalito.
  27. Silva, W.P., Precker, J.W., Silva, C.M.D.P.S., Silva, C.D. P.S., Silva, D.D.P.S. and Lima, A.G.B. (2007) Calculation of the uncertainty in the determination of the equilibrium moisture content of pumpkin seed flour. International Journal of Food Engineering, 3, 1098.

Journal Menu >>