American Journal of Plant Sciences
Vol.5 No.4(2014), Article ID:43264,11 pages DOI:10.4236/ajps.2014.54064
Foliar Nutrient Balance Standards for Maize (Zea mays L.) at High-Yield Level
![]()
1Departamento de Solos e Adubos, Unesp, Universidade Estadual Paulista, Jabotocabal, Brazil; 2ERSAM, Department of Soils and Agrifood Engineering, Université Laval, Québec, Canada.
Email: *leon-etienne.parent@fsaa.ulaval.ca
Copyright © 2014 Viviane Cristina Modesto et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Viviane Cristina Modesto et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 14th, 2013; revised January 21st, 2014; accepted February 14th, 2014
KEYWORDS
Compositional Data Analysis; Critical Range; Diagnosis and Recommendation Integrated System; DRIS; Ionomics; Nutrient Balance; Nutrient Interactions
ABSTRACT
Maize is one of the most nutrient demanding staple crops. Tissue nutrient diagnosis of maize is currently conducted using critical nutrient concentration or dual ratio ranges, but such diagnoses are pathological as biased by data redundancy, sub-compositional incoherence and non-normal distribution. The use of orthogonal balances, a compositional data analysis technique, avoids such biases. Our objective was to develop foliar nutrient balance standards for maize. We collected 758 grain yields (15.5% moisture content) and foliar samples at silk stage in maize fields of southern Quebec, Canada, and analyzed ten nutrients in tissues (N, P, K, Ca, Mg, B, Cu, Zn, Mn, Fe). Nutrients were arranged into ad hoc balances and computed as isometric log ratios (ilr). An optimized binary classification performed by a customized receiver operating characteristic procedure showed that a critical Mahalanobis distance of 4.21 separated balanced from imbalanced specimens about yield cut-off of 11.83 Mg grain·ha−1 with test performance of 86%. Quebec maize balance standards differed from published standards computed from DRIS norms collected in other agroecosystems. The Redfield N/P ratio in maize leaves was found to be the least variable balance across regions of the world. The DRIS dual ratios and raw concentration values were found to be geometrically inadequate for conducting diagnosis. The unbiased nutrient balance diagnosis combined the critical Mahalanobis distance and a mobile representation of nutrient balances with ilr means of true negative (TN) specimens centered at fulcrums and back-transformed ilr values of TN specimens into raw concentrations loading the buckets below. Nutrients can be appreciated as relative shortage, adequacy or excess in the concentration domain following statistical analysis and diagnosis in the unbiased balance domain.
1. Introduction
Maize is one of the most nutrient demanding staple crops. As an aid to assess the nutrient status of maize agroecosystems, tissue analytical data are currently diagnosed using critical nutrient concentration ranges (CNCR) [1] or dual ratios [2]. However, the CNCR is biased for not accounting for nutrient interactions [3]. Although dual nutrient ratios may reflect interactions [4], there are D ´ (D − 1)/2 possible dual ratios in a D-parts composition; most of them are redundant and spuriously correlated because a D-parts composition has only D − 1 degrees of freedom [5]. Dual ratios may thus lead to misinterpretations when correlated with yield [6]. The Diagnosis and Recommendation Integrated System (DRIS) integrates dual ratios into D indices [4]. Crop nutrient diagnosticians conduct CNCR and DRIS separately to identify the most limiting nutrients [7]. Because CNCR and DRIS are both methodologically biased [6,8,9], hence pathological, they may lead to conflicting interpretations [10-13].
Nutrients in fresh or dry tissue matter are related not only physiologically through interactions [3,14] but also numerically [15] due to closure forcing relative amounts to add up to 100%. Indeed, tissue analytical data belong to the class of compositional data that are strictly positive, intrinsically related to each other and constrained between zero and the unit of measurement [15]. Using raw compositional data to conduct linear statistical analysis leads to methodological biases caused by redundancy of information, non-normal distribution and sub-compositional incoherence [16]. Because one component is redundant, the compositional vector has D − 1 degrees of freedom [5]. To avoid biases, [15] proposed using the additive log ratio (alr) and the centred log ratio (clr) transformations. The alr generates D − 1 variables, i.e. equal to the number of degrees of freedom in a compositional vector, but does not preserves Euclidean distances; the clr preserves Euclidean distances, but generates D variables from a composition of D parts, hence keeping redundancy of information that produces a singular covariance matrix. The isometric log ratio transformation (ilr) [17] avoids the drawbacks of alr and clr.
The DRIS involves adding up variables but additivity is not supported by proper geometry. The inappropriate DRIS geometry has been rectified using clr (CND-clr) [18]. The ilr (CND-ilr) not only fits the Euclidean geometry perfectly but can also illustrate nutrient relationships as hierarchically arranged binary balances between groups of nutrients to describe the system under study [19]. The ilr concept was found to be the most appropriate for conducting multivariate analysis [20] and plant nutrient diagnosis [8,19,21,22].
Our objectives were to 1) develop ilr standards for maize in Quebec, Canada, 2) demonstrate the pathological behavior of DRIS and the critical raw concentration range models, and 3) compare the Quebec maize balance standards to published nutrient standards.
2. Theory
2.1. Compositional Data Space
A compositional vector is closed or constant-sum constrained as follows [15]:
 (1)
(1)
where ci is the ith part of a composition constrained to the unit of measurement κ. Because plant nutrient concentrations are usually reported as amounts relative to dry matter, a filling value (Fv) can be computed by subtracting the sum of analyzed nutrients (N, P, K, Ca, Mg, etc.) to the total dry matter. The Fv is thus a part of the composition. Its inclusion allows back-transforming the ilr values (see next section) into concentration values with familiar units of measurement.
2.2. The Isometric Log Ratio (ilr)
The ilr technique [17] generates D − 1 non-overlapping orthogonal log-contrasts that are interpreted as balances. Balances are designed according to a D × (D − 1) matrix named the sequential binary partition (SBP). Each row of the SBP defines a balance of the components in columns: in each row, parts labeled “+1” as group numerator are balanced with parts labeled “−1” as group denominator and parts labeled “0” are excluded. Each sequential row splits into sub-compositions until each subset contains a single part. Balances are computed as follows [23]:
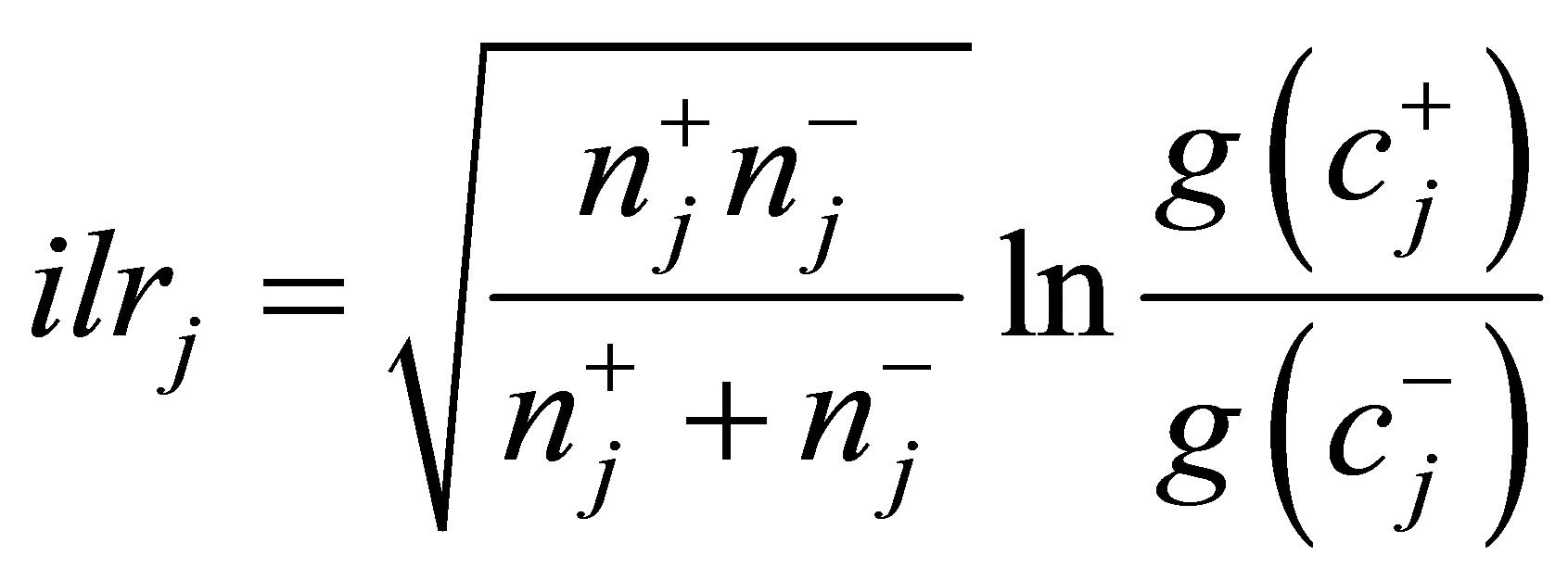 (2)
(2)
where, in the jth row of the SBP,  and
and 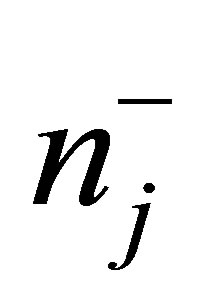 are the numbers of components in the “+1” and the “−1” subsets, respectively, g (
are the numbers of components in the “+1” and the “−1” subsets, respectively, g ( ) and g (
) and g (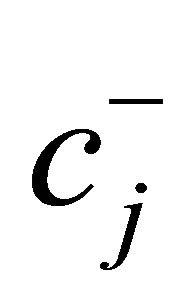 ) are geometric means of components in the “+1” and “−1” subsets, respectively.
) are geometric means of components in the “+1” and “−1” subsets, respectively.
The orthogonal coefficient, 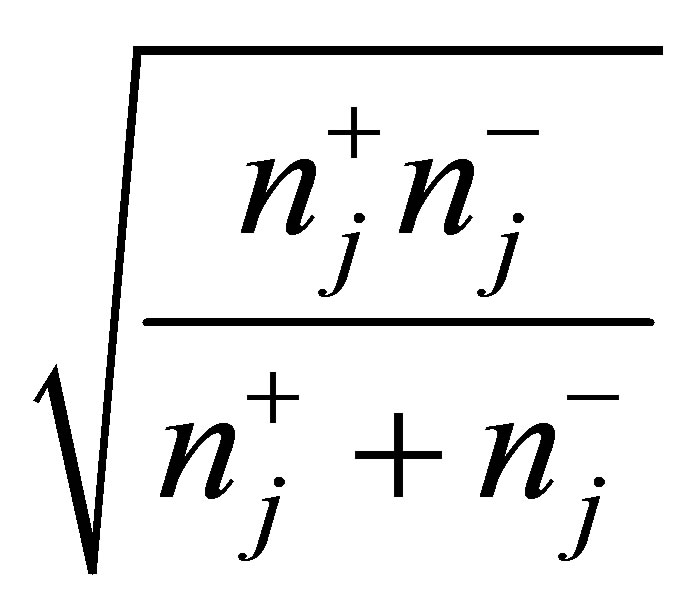 , assures that ilrs are orthogonal to each other. In this paper, balances are named as “[−1 subset|+1 subset]” to locate negative numbers to the left as in algebra. The distance between a diagnosed composition and the reference one for high yielding crops is computed as a Mahalanobis distance as follows:
, assures that ilrs are orthogonal to each other. In this paper, balances are named as “[−1 subset|+1 subset]” to locate negative numbers to the left as in algebra. The distance between a diagnosed composition and the reference one for high yielding crops is computed as a Mahalanobis distance as follows:
 (3)
(3)
where ilri is the ilr vector of the diagnosed composition, 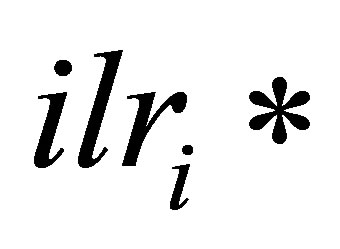 is the ilr vector of the reference composition, T indicates a transposed matrix, and
is the ilr vector of the reference composition, T indicates a transposed matrix, and 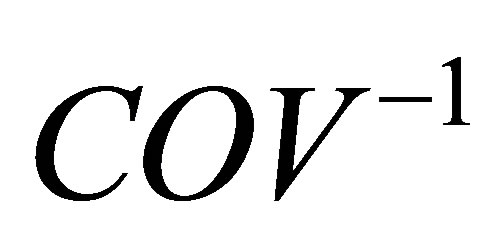 is the inverse covariance matrix.
is the inverse covariance matrix.
The compositional mobile is a metaphor that represents the balance system as shown in Figure 1. An ideal set of balances (white circles) is located at the center of horizontal bars and an observational set, dragged by concentrations in buckets, is presented for comparison. Analyses and diagnoses are conducted in the balance domain, whereas the associated concentrations are appreciated in the concentration domain. Even though Mg and N appear to be quite on par with the ideal composition shown by the horizontal line across the buckets, they appear to be misbalanced at fulcrums. Because a nutrient cannot be appreciated without relating it to at least another one, working with balances is of paramount importance.
2.3. Designing a Sequential Binary Partition (SBP)
There are D ´ (D − 1)/2D−1 possible balances that can be elaborated from a D-parts composition [24]. However,

Figure 1. Schematic representation of a compositional mobile design with fulcrums and buckets.
the balances between plant nutrients should reflect the way the designer conceives the system, whether based on prior and expert knowledge [6,8,21,22], e.g. in terms of plant physiology, the agronomic practice or some statistical relationships [6,9] or by exploratory biplot analysis across clrs-where 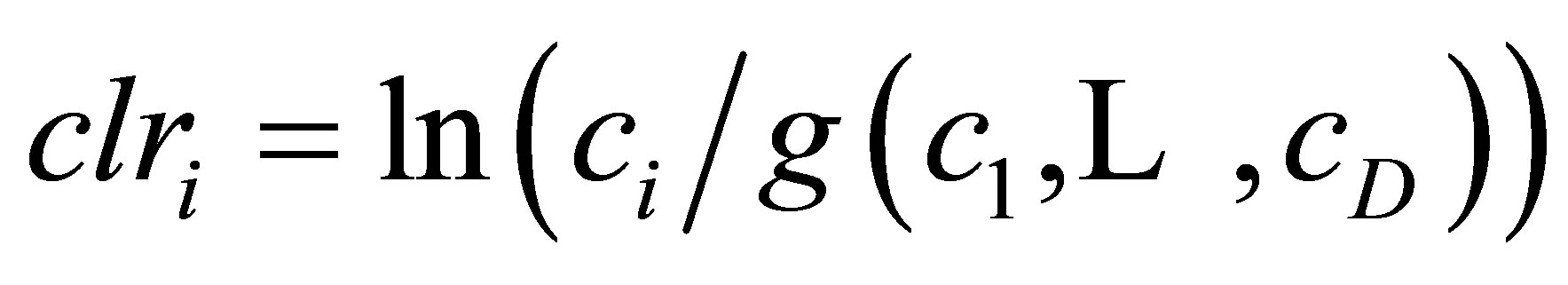 [5]. In any event, the results of multivariate statistical analyses across ilr variables are not influenced by the selected SBP. Indeed, the Euclidean distance matrix of ilrs is independent of SBP: switching from a SBP to another one consists in drawing another set of orthogonal axes across the same data scatter, resulting in data translation, rotation and symmetry. However, the analyst can benefit from selecting interpretable balances.
[5]. In any event, the results of multivariate statistical analyses across ilr variables are not influenced by the selected SBP. Indeed, the Euclidean distance matrix of ilrs is independent of SBP: switching from a SBP to another one consists in drawing another set of orthogonal axes across the same data scatter, resulting in data translation, rotation and symmetry. However, the analyst can benefit from selecting interpretable balances.
We designed a SBP (Table 1) based on prior knowledge of nutrient interactions [3]. Nutrients were first contrasted with the filling value. Macronutrients and B were separated from cationic micronutrients. Macronutrient anions (N, P) were contrasted with macronutrient cations (K, Ca, Mg) as suggested in nutrient solution studies [25]. Macronutrient anions were further subdivided into a [P|N] balance [26] and cationic balances [14]. The Cu, Zn, Fe and Mn contrasts involve considering both soil properties and fungicide formulations and could be supported by biplot analysis.
2.4. Attempt to Transform DRIS Norms into Balance Standards
The macronutrient DRIS dual ratio norms retrieved from literature were converted into ilr variables. For N/P and Ca/Mg, the conversion was straightforward as follows:
 (4)
(4)
where r = 1 and s = 1 In case of multi-ratios, the ilr formula was decomposed into linear combinations of dual ratios. The [Ca, Mg K|N, P] balance was decomposed as follows (excluding the orthogonal coefficient):
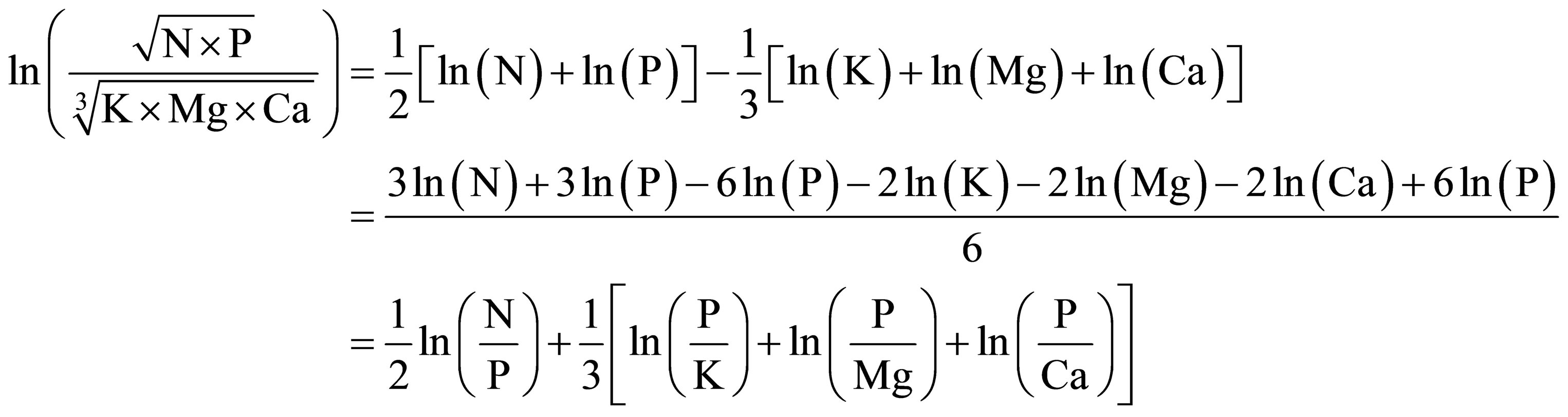 (5)
(5)
Equation (5) was multiplied by 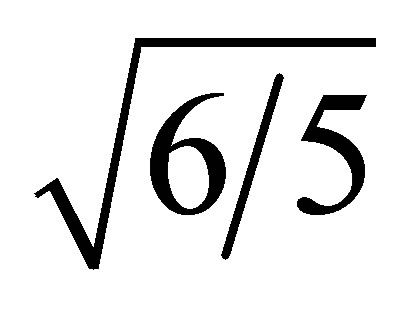 to obtain the corresponding ilr value.
to obtain the corresponding ilr value.
The [Ca, Mg|K] balance was re-arranged as follows (excluding the orthogonal coefficient):
 (6)
(6)
Equation (6) was multiplied by 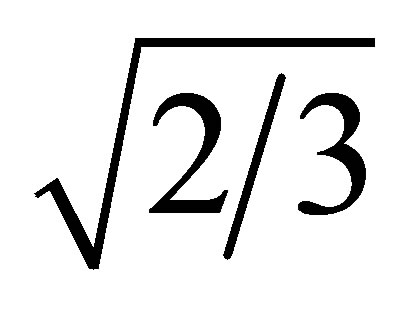 to obtain the ilr value.
to obtain the ilr value.
2.5. Receiver Operating Characteristic
Binary classification relates a predictor and a response. In crop science, one can use the yield as response. As for prediction, [8] used the Mahalanobis distance between an observation and the center of a reference group (with its associated covariance), corresponding to high yield and adequate nutrient compositions as defined by nutrient balances. The lower the distance, the closer the nutrient balance profile of the observation is to the one of the reference group. A predictor delimiter must be deter-
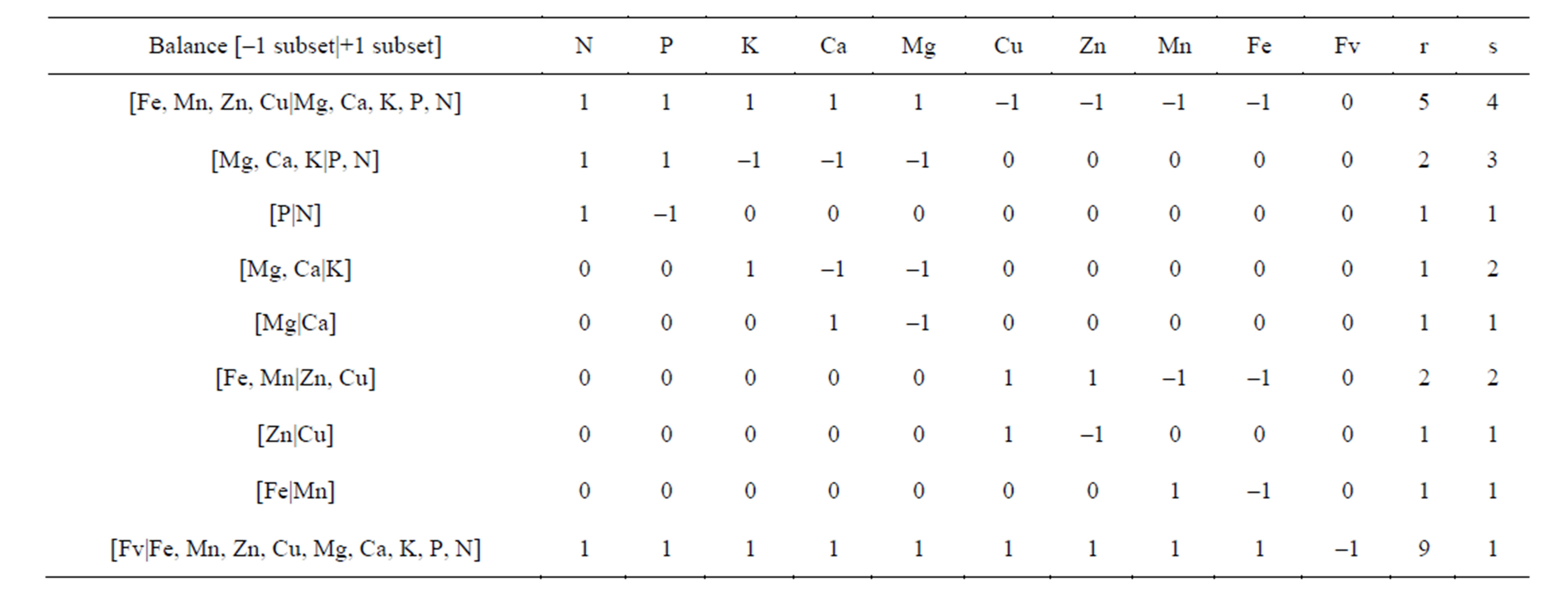
Table 1. Sequential binary partition (SBP) of maize nutrients based on prior knowledge and biplot analysis.
mined to separate adequate from inadequate nutrient compositions. Also, because in the case under study the response is continuous (rather than binary, as found in most clinical binary classifications), a response delimiter is also needed. Once delimiters are set, four quadrants are created:
Ÿ TP (true positive): low yield, above critical nutrient predictor.
Ÿ FP (false positive, type I error): high yield above critical nutrient predictor.
Ÿ TN (true negative): high yield, below critical nutrient predictor (reference group).
Ÿ FN (false negative, type II error): low yield, below critical nutrient predictor.
Delimiters must be determined using performance criteria. The receiver operating characteristic (ROC) curve can be used for this purpose [8]. For a given response delimiter and a series of possible predictor delimiters, a ROC curve relates sensitivity to specificity. The optimal predictor is the one maximizing the Youden index, i.e. J = sensitivity + specificity – 1) ([34]). The area under the ROC curve (AUC) is the probability that a randomly chosen low yielder will return a higher Mahalanobis distance than a randomly chosen high yielder.
In survey analyses, a reference group must be defined. However, the Mahalanobis distance from TNs’ centroid (MTN, the predictor) cannot be computed without knowing a priori which observations could be classified as TNs. An iterative procedure is thus needed, as follows. “For a given response (crop yield) delimiter, the predictor is initiated using high-yielders as reference specimens for computing MHY. Thereafter, a predictor delimiter is selected and its barycenter and co-variance are computed among newly delineated TN specimens in order to compute MTN. The MTN is iterated until two iterations classify observations identically.” [8]
3. Materials and Methods
3.1. Data Set
We collected maize yield and foliar analytical data at 758 locations (farmers’ fields and experimental plots) in the St-Lawrence Lowlands of southern Quebec, Canada. Ear leaves were collected in July at silk stage. Foliar N was determined by combustion (CNS-Leco 2000). The P, K, Ca, Mg, Zn, Cu, Mn, Fe, and B concentrations were determined by IPC-OES after digestion in a mixture of nitric and perchloric acids [27]. Grain was machine-harvested in large plots and hand-harvested in small plots. Grain yield was expressed on 15.5% moisture basis.
3.2. Statistical Analysis
Statistical computations were conducted in the R statistical environment [28], using the R “compositions” package [29]. Outliers were discarded at the 0.01 level using R’s “mvoutlier” package [30]. Biplot analysis was conducted using clr-transformed data [31]. The MoorePenrose pseudo-inversion was used to avoid singularities in the inversion of the covariance matrix needed for computations of Mahalanobis distances [32]. Computations needed for the optimization of the binary classification and the DRIS were performed with R, using custom functions that can be provided upon request (serge-etienne.parent.1@ulaval.ca). To assure statistical significance, the minimum number of points in the TN or TP quadrants was set to 10% of the data set.
4. Results
4.1. Outliers
A number of 106 outliers were discarded from the data set, representing nearly 14% of the whole data set, leaving 689 data for subsequent analysis.
4.2. Biplot Analysis and Sequential Binary Partition (SBP)
The SBP (Table 1) was elaborated based on prior knowledge for macronutrients and clr biplot analysis for cationic micronutrients (Figure 2). The Mn and Fe were found to be in the opposite direction, while Cu and Zn were nearly orthogonal to each other. The [Fe|Mn] and [Zn|Cu] balances were thus retained in the SBP.4.3. Calibration of Nutrient Balance Standards
Considering a minimum of 69 observations either the TN or TP quadrant, the binary classification relating the Mahalanobis distance (predictor) to maize yield showed a maximum AUC of 86% and yield delimiter of 11,825 kg·ha−1 (Figure 3(a)). The ROC curve corresponding to this yield delimiter is presented in Figure 3(b). The maximum of the Youden’s index was found at 0.68, for both specificity and sensitivity equal to 0.84, corresponding to a Mahalanobis distance delimiter of 4.21. The resulting binary classification is shown in Figure 3(c). There were a number of 13 (2% of the data set) false positive and 98 (14% of the data set) false negative specimens. The true positive group comprised 74% of the data set (509). Nine percent of the population (69 specimens) was classified as true negative (TN). All TN specimens were grown on 1997 and 1999 where climatic conditions were highly favorable to the maize.
Nutrient balance standards are the means and covariance matrix of the TN group (Table 2), because both are needed to compute the Mahalanobis distance (Equation (3)). The compositional mobile presented in Figure 4 shows the compositional mean of TN at fulcrum compared to the balance means of TP specimens, both associated with their 95% confidence intervals. There were univariate significant differences between the following means of TN and TP balances: [Mg, Ca|K], [Mg|Ca], [Fe, Mn|Zn, Cu], [Zn|Cu], and [Fe|Mn].
After back-transforming ilr standards into familiar concentration units, the TN group showed the central values presented in buckets of the mobile plot in Figure 4: 29.8 g N·kg−1, 2.7 g P·kg−1, 24.6 g K·kg−1, 4.9 g Ca·kg−1, 1.6 g Mg·kg−1, 936.3 g Fv·kg−1, 8 mg Cu·kg−1, 29 mg Zn·kg−1, 44 mg Mn·kg−1, and 94 mg Fe·kg−1. No confidence intervals can be computed as concentration ranges because concentration values are compositional and subjected to interactions. Evidence of pathological behavior using concentration values is presented in Figure 5(a) where Mahalanobis distances were consistently inflated for concentration values compared to those computed from unbiased ilrs. Because the balances and concentrations are integrated into a mobile setup, the diagnosis cannot produce conflicting results as reported above for joint DRIScritical concentration range diagnoses.
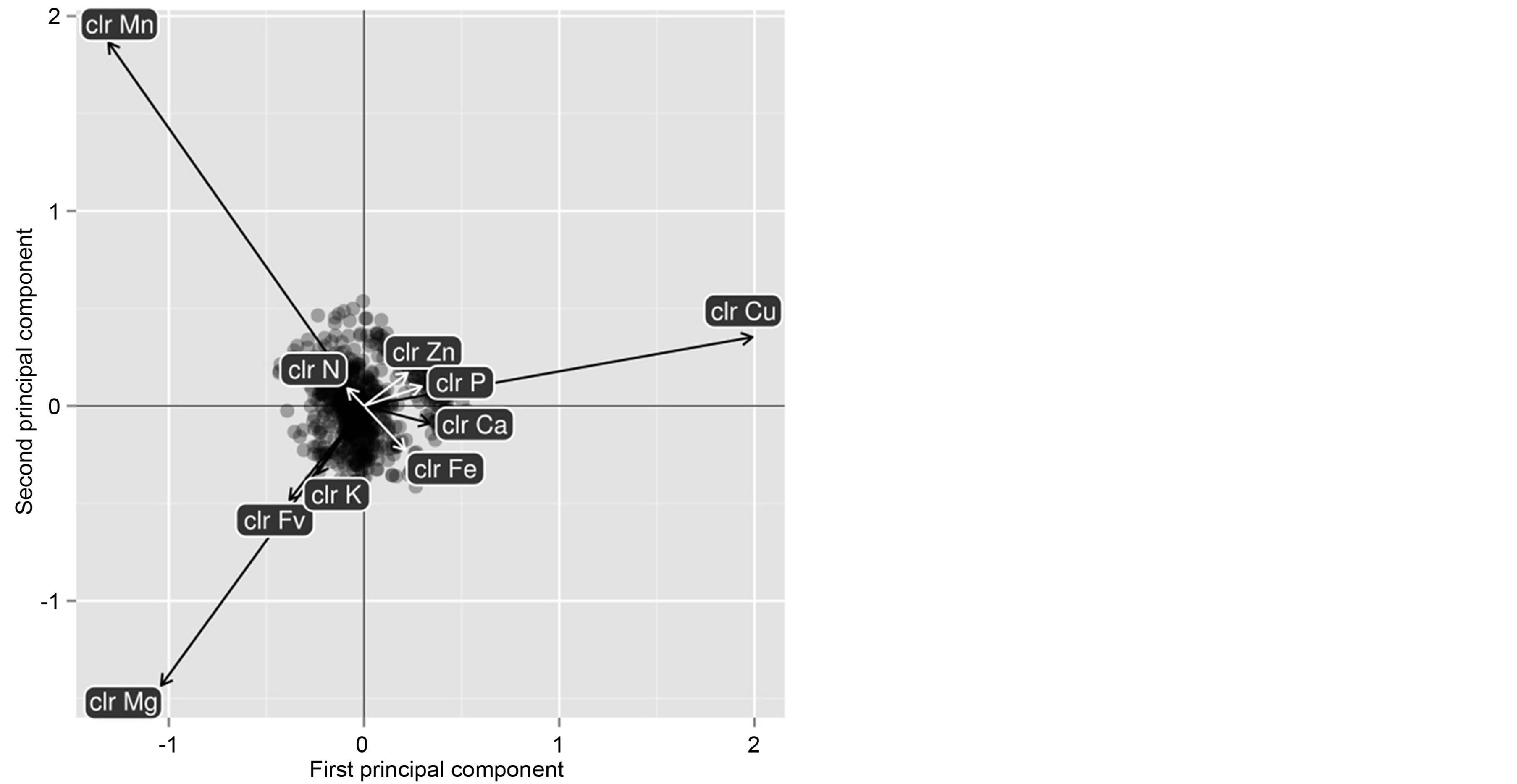
Figure 2. Biplot showing relationships among nutrients in the Quebec maize data set.
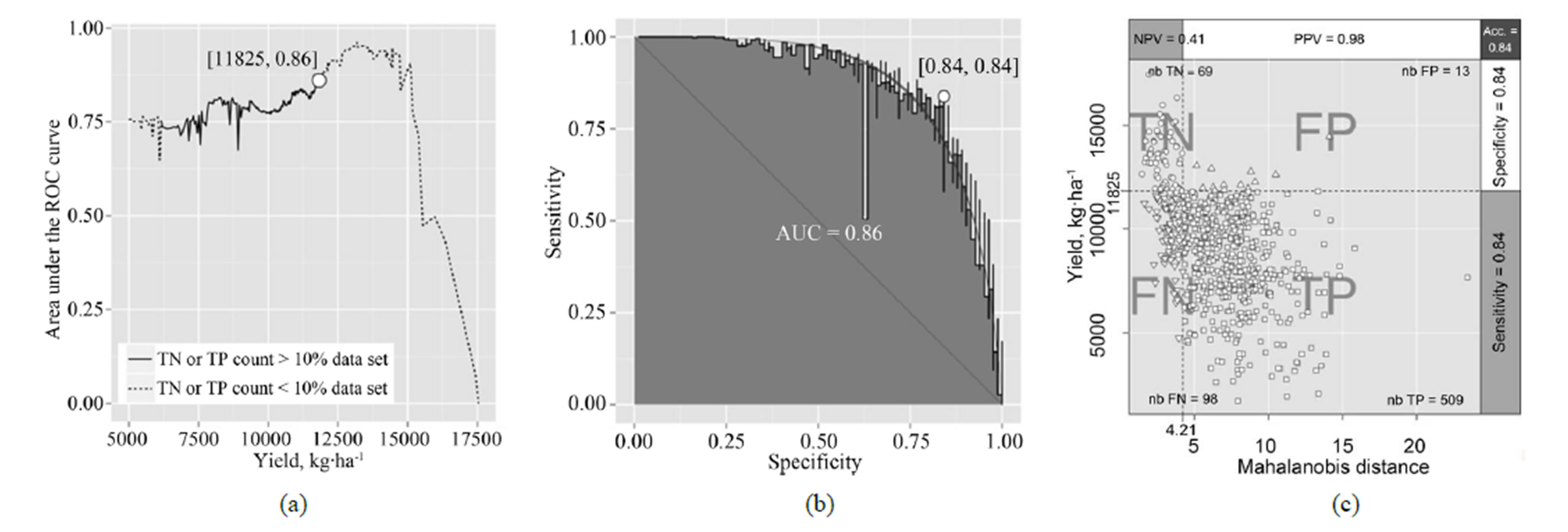
Figure 3. (a) Area under the ROC curve versus cut-off yield and (b) ROC curve for yield cut-off of 11,825 kg·ha−1 (c) Binary classification of data.
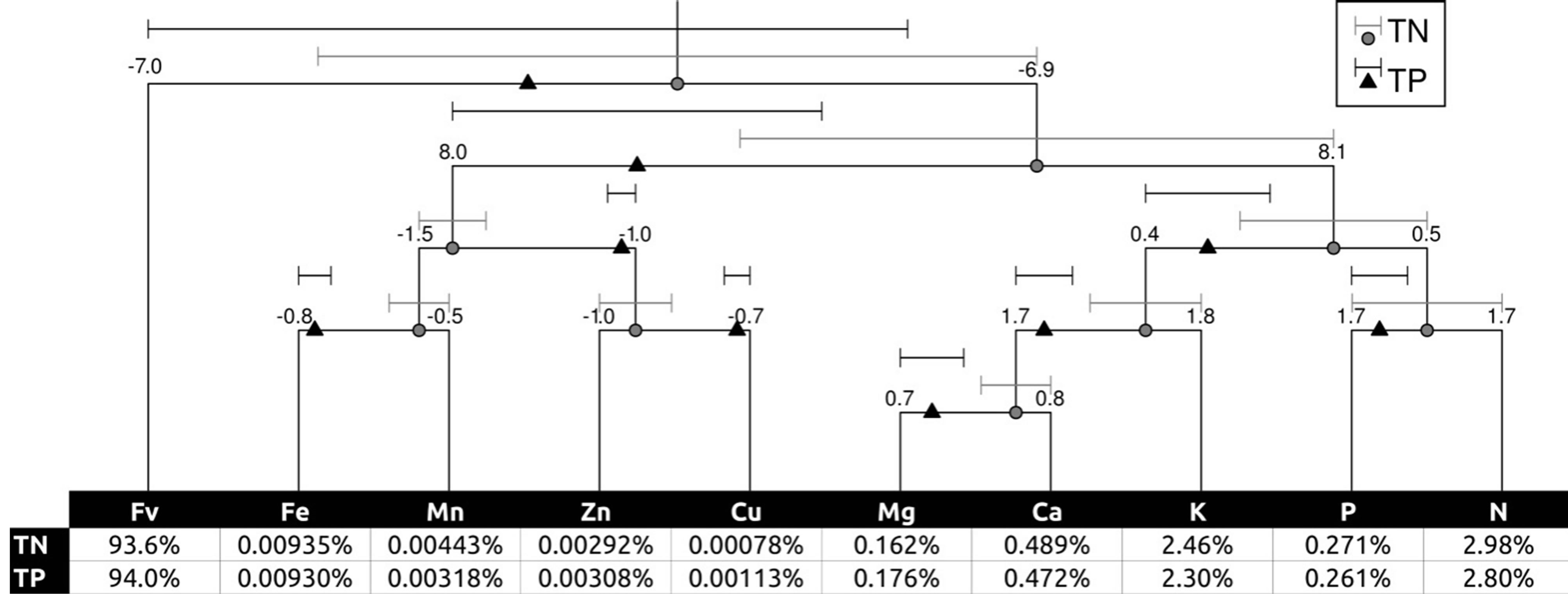
Figure 4. Compositional mobile illustrating nutrient equilibrium in foliar tissues of TN and TP specimens. Concentrations in weighing pans (buckets) down below are back-transformed ilr means.

Table 2. Nutrient balance standards for the Quebec maize data set.
4.4. Comparison of Nutrient Balance Standards Worldwide
The DRIS proved to be a noisy, pathological, diagnostic system for maize. Indeed, there was a large discrepancy between the geometrically inadequate DRIS imbalance index [4] and the unbiased ilr-based Mahalanobis distance (Figure 5(b))—for sake of comparison, the Fv component and the associated balance was removed from the DRIS and the ilr Mahalanobis distance, respectively. In addition, the DRIS dual ratio standards were not symmetrical as often reported [40,41], i.e. (X/Y) generally differed from 1/(Y/X) for nutrients X and Y. In addition, coefficients of variation were heterogeneous across studies (13% - 101%).The comparison between the balance concept and DRIS was thus conducted with the only objective to show the large variation in maize nutrient standards worldwide. The Quebec DRIS dual ratios of TN specimens computed from ilr means back-transformed to raw concentration values were compared to literature standards [35-43]. There were large discrepancies between DRIS ratios worldwide (Table 3). Nutrient balance standards for grain corn in Quebec were also compared to literature DRIS ratio standards converted to nutrient balances (Table 4). There were again large discrepancies between balances worldwide. The most consistent balance was [P|N] and the most variable was [Mg, Ca|K]. The Quebec [P|N] and [Mg|Ca] balances were the 9th highest while the Quebec [Mg, Ca|K] balance was the
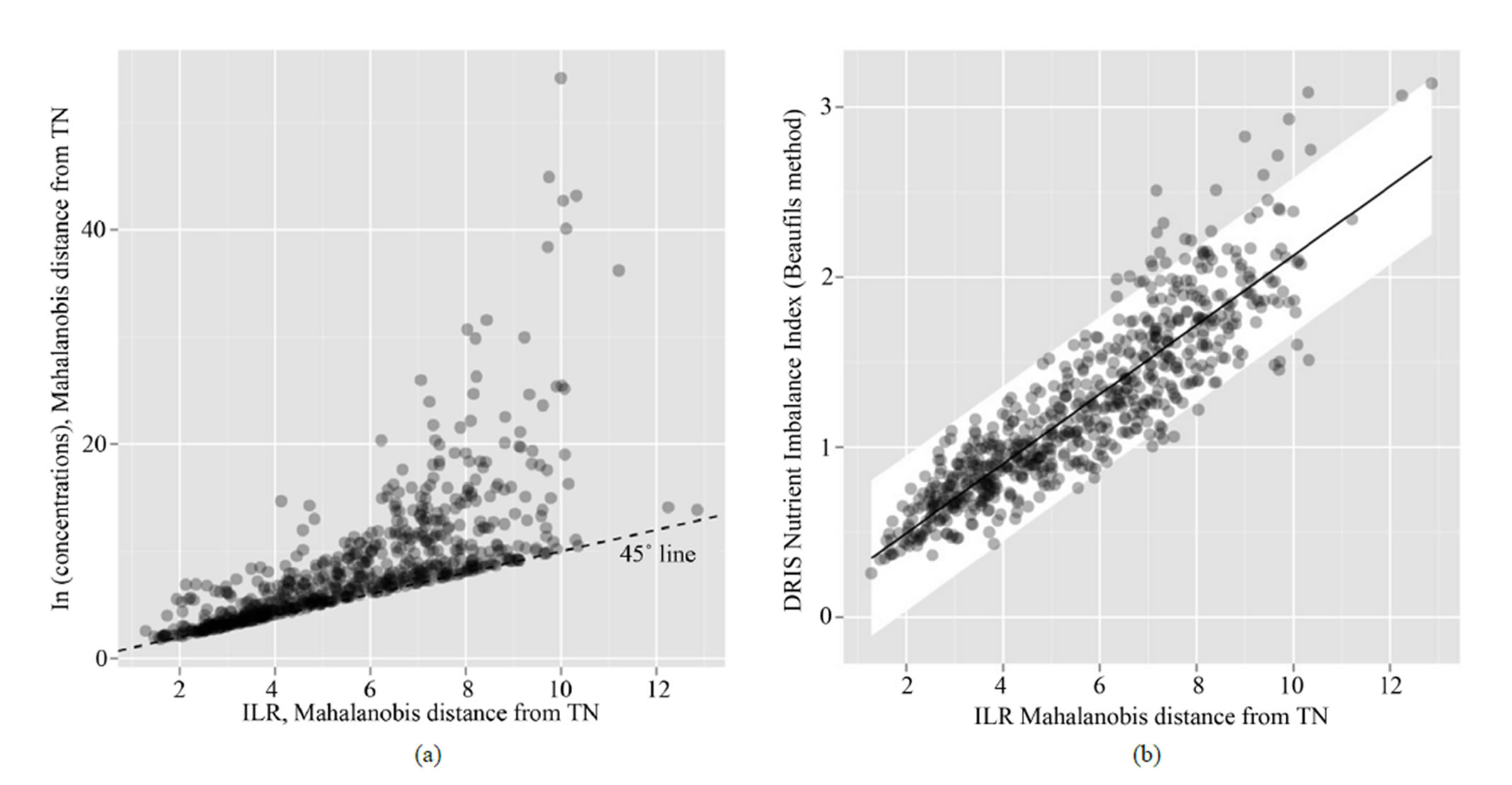
Figure 5. Bias measured by discrepancy between the Mahalanobis distance from the TN population across the isometric log ratios (x-axis) and (a) the Mahalanobis distance from the TN population across the natural log of concentrations (y-axis) and (b) the DRIS nutrient imbalance index (y-axis).

Table 3. Comparison of maize DRIS ratios from literature DRIS ratios or computed from Quebec survey.
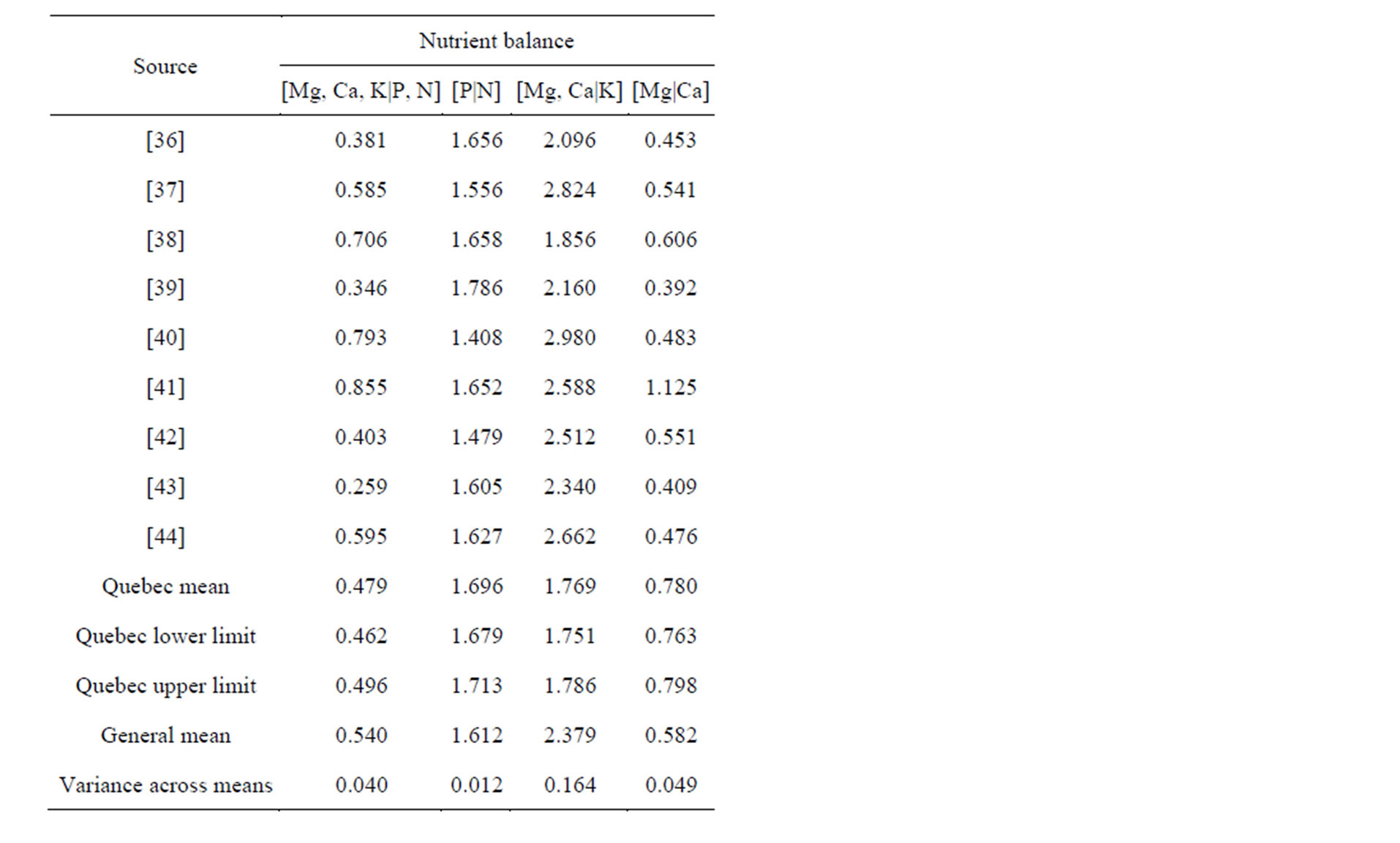
Table 4. Comparison between literature DRIS ratios converted to nutrient balances and nutrient balance standards elaborated for grain corn in Quebec.
lowest and the [Mg, Ca, K|N, P] Quebec balance was near median.
5. Discussion
Although there is no standard for binary classification adequacy in plant nutrition, we considered that an AUC of 86%, comparable to tests in clinical biology [33,44], provided evidence for the informative relationship between yield and foliar nutrient signature. The AUC indicates the performance of the classification: a good performance is associated with a large area, reaching a maximum of 1, and a random classification will return an area close to 0.5. The true positive group comprised 74% of the specimens, indicating that nutrient management could be improved in those fields. In comparison with TN central values in Figure 4, the critical nutrient ranges proposed by [1] were: 27 - 40 g N·kg−1, 2.5 - 5.0 g P·kg−1, 17 - 30 g K·kg−1, 2.1 - 10 g Ca·kg−1, 2 - 10 g Mg·kg−1, 6 - 20 mg Cu·kg−1, 25 - 100 mg Zn·kg−1, 20 - 200 mg Mn·kg−1, and 21 - 250 mg Fe·kg−1. Hence, only Mg was outside current published critical ranges.
On the other hand, DRIS has inadequate geometry that could not justify the additivity of variables [8]. [45] proposed to log transform dual ratios to reduce variance in DRIS standards and produce variances and means independent of dual ratio expression. Nutrient log ratio standards for maize have been further rectified using the clr transformation [46]. However, the clr is influenced by large variations in some components that affect the geometric mean used as denominator [20] such as cationic micronutrients used in fungicide formulations. The most appropriate log ratio transformation for the multivariate analysis of compositional data is the ilr, thanks to its Euclidean geometry [17,20], that preserves all the information from the raw data (the clr matrix is singular if one clr is not removed before conducting multivariate analysis) and allows computing multivariate distances across balances.
The large discrepancies between DRIS ratios indicated regional specificities. Nutrient balances reconstituted from published DRIS dual ratios showed that maize has high phenotypic plasticity across soil and climatic conditions, hence denying any universality of nutrient balance standards. The most consistent balance was [P|N] and the most variable was [Mg, Ca|K], reflecting high variability in regional conditions of soil, climate, and crop management. The Redfield N/P ratio varied between 7.3 and 12.5 at silk stage. The reference N/P ratio in Quebec was 11 after back-transforming ilr of 1.696. The balance between protein and rRNA syntheses results in a stable biochemical attractor that produces a given protein: rRNA or N/P ratio [26]. Indeed, [47] reported N/P ratios in the range of 10 to 20 across plant species and physiological ages. The physiological age of the plant part is an important factor that affects nutrient concentrations [14]. This is why nutrient levels and ratios should be compared to standards at the same physiological age [9,48]. The N/P ratio close to 10 seemed to be appropriate for maize at silk stage.
The TN specimens represented data for 1997 and 1999 only. Therefore, nutrient balance standards reflected exceptional climatic and soil conditions during those productive years. Such standards thus informed on nutrient balance targets to reach under the most favorable growing conditions. On the other hand, because all nutrients but Mg were within published optimum ranges in the TN group, this relatively low Mg concentration possibly resulted from Mg dilution at high yield level. Although this apparent Mg shortage may result in lower proportion of proteins and accumulation of carbohydrates, it does not necessarily lead to low yield [14]. Nevertheless, field trials are needed to validate nutrient balance standards.
6. Conclusion
This paper showed that nutrient balances and raw concentration values can be interpreted coherently using a mobile-fulcrums-buckets setup that combines a balance domain for nutrient diagnosis and a concentration domain for nutrient level appreciation. Nutrient balance standards are the means and the covariance matrix of ilr transforms for a population of true negative specimens determined following a customized iterative receiver operating characteristic (ROC) procedure. Nutrient balance standards for maize grown in Quebec differed from those from other regions of the world except for the Redfield N/P ratio that varied least possibly due to its role in regulating protein metabolism. The balance standards need to be further validated with field fertilizer trials.
Acknowledgements
We acknowledge the financial support of the Coordenação de Aperfeiçoamento de Pessoal de Nível SuperiorCAPES, the International Council for Canadian Studies, the Natural Sciences and Engineering Council of Canada (CRDPJ 385199-09) and Canadian farm partners as follows: Cultures Dolbec Inc., St-Ubalde, Québec, Canada; Groupe Gosselin FG Inc., Pont Rouge, Québec, Canada; Agriparmentier Inc. and Prochamps Inc., Notre-Damedu-Bon-Conseil, Québec, Canada; Ferme Daniel Bolduc et Fils Inc., Péribonka, Québec, Canada. We thank Patricia Leduc, Catherine Tremblay and Roger Rivest for data collection.
REFERENCES
- J. B. Jones Jr., B. Wolf and H. A. Mills, “Plant Analysis Handbook: A Practical Sampling, Preparation, Analysis, and Interpretation Guide, Micro Macro Intl.,” Athens, 1991.
- E. Malavolta, “Manual de Nutrição de Plantas,” Editora Agronomica Ceres, São Paulo, 2006, p. 638.
- S. R. Wilkinson, “Nutrient Interactions in Soil and Plant Nutrition,” In: M. E. Sumner, Ed., Handbook of Soil Science, CRC Press, Boca Raton, 2000, pp. D89-D112.
- J. L. Walworth and M. E. Sumner, “The Diagnosis and Recommendation Integrated System (DRIS),” Advances in Soil Science, Vol. 6, 1987, pp. 149-188. http://dx.doi.org/10.1007/978-1-4612-4682-4_4
- J. Aitchison and M. Greenacre, “Biplots of Compositional Data,” Journal of the Royal Statistical Society Series C Applied Statistics, Vol. 51, No. 4, 2002, pp. 375-392. http://dx.doi.org/10.1111/1467-9876.00275
- S.-É. Parent, L. E. Parent, D. E. Rozane, A. Hernandes and W. Natale, “Nutrient Balance as Paradigm of Soil and Plant Chemometrics,” In: R. N. Issaka, Ed., Soil Fertility, Intech, 2012, pp. 83-114. http://dx.doi.org/10.5772/53343
- P. G. S. Wadt and D. J. Silva, “Acurácia Do Diagnóstico Nutricional de Pomares de Mangueiras Obtido Por Três Fórmulas DRIS,” Pesquisa Agropecuária Brasileira, Vol. 45, No. 10, 2010, pp. 1180-1188. http://dx.doi.org/10.1590/S0100-204X2010001000018
- S.-É. Parent, L. E. Parent, D. E. Rozane and W. Natale, “Nutrient Balance Ionomics: Case Study with Mango (Mangifera indica),” Frontiers in Plant Science, Vol. 4, 2013, Article 449.
- S.-É. Parent, L. E. Parent, J. J. Egozcue, D. E. Rozane, A. Hernandes, L. Lapointe, V. Hébert-Gentile, et al., “The Plant Ionome Revisited by the Nutrient Balance Concept,” Frontiers in Plant Science, Vol. 4, No. 39, 2013, pp. 1- 10.
- G. G. C. Da Silva, J. C. L. Neves, V. H. Alvarez and F. P. Leite, “Nutritional Diagnosis for Eucalypt by DRIS, MDRIS, and CND,” Scientia Agricola, Vol. 61, No. 5, 2004, pp. 507-515. http://dx.doi.org/10.1590/S0103-90162004000500008
- F. R. Blanco-Macías, R. D. Magallanes-Quintanar, R. Valdez-Cepeda, E. Vázquez-Alvarado, E. Olivares-Sáenz, E. Gutiérrez-Ornelas and J. A. Vidales-Contreras, “Comparison between CND Norms and Boundary-Line Approach Nutrient Standards: Opuntia Ficus-Indica L. Case. R. Chapingo,” Serie Horticultura, Vol. 15, No. 2, 2009, pp. 217-223.
- H. Huang, C. X. Hu, Q. Tan, X. Hu, X. Sun and L. Bi, “Effects of Fe-EDDHA Application on Iron Chlorosis of Citrus Trees and Comparison of Evaluations on Nutrient balance with Three Approaches,” Scientia Horticulturae, Vol. 146, 2012, pp. 137-142. http://dx.doi.org/10.1016/j.scienta.2012.08.015
- L. W. I. Wairegi and P. J. A. Van Asten, “Norms for Multivariate Diagnosis of Nutrient Imbalance in Arabica and Rosusta Coffee in the East African Highlands,” Experimental Agriculture, Vol. 48, No. 3, 2012, pp. 448- 460. http://dx.doi.org/10.1017/S0014479712000142
- P. Marschner, “Marschner’s Mineral Nutrition of Higher Plants,” 3rd Edition, Academic Press, London, 2011.
- J. Aitchison, “The Statistical Analysis of Compositional Data, Monographs on Statistics and Applied Probability,” Chapman & Hall Ltd., London, 1986. http://dx.doi.org/10.1007/978-94-009-4109-0
- J. Bacon-Shone, “A Short History of Compositional Data Analysis,” In: V. Pawlowsky-Glahn and A. Buccianti, Eds., Compositional Data Analysis: Theory and Applications, John Wiley and Sons, New York, 2011, pp. 3-11. http://dx.doi.org/10.1002/9781119976462.ch1
- J. J. Egozcue, V. Pawlowsky-Glahn, G. Mateu-Figueras and C. Barceló-Vidal, “Isometric Logratio Transformations for Compositional Data Analysis,” Mathematical Geology, Vol. 35, No. 3, 2003, pp. 279-300. http://dx.doi.org/10.1023/A:1023818214614
- L. E. Parent and M. Dafir, “A Theoretical Concept of Compositional Nutrient Diagnosis,” Journal of the American Society for Horticultural Science, Vol. 117, No. 2, 1992, pp. 239-242.
- L. E. Parent, “Diagnosis of the Nutrient Compositional Space of Fruit Crops,” Revista Brasileira de Fruticultura, Vol. 33, No. 1, 2011, pp. 321-334. http://dx.doi.org/10.1590/S0100-29452011000100041
- P. Filzmoser, K. Hron and C. Reimann, “Univariate Statistical Analysis of Environmental (Compositional) Data: Problems and Possibilities,” Science of Total Environment, Vol. 407, No. 23, 2009, pp. 6100-6108. http://dx.doi.org/10.1016/j.scitotenv.2009.08.008
- L. E. Parent, S.-É. Parent, V. Hébert-Gentile, K. Naess and L. Lapointe, “Mineral Balance Plasticity of Cloudberry (Rubus Chamaemorus) in Quebec-Labrador,” American Journal of Plant Science, Vol. 4, No. 7, 2013, pp. 1508-1520.
- L. E. Parent, S.-É. Parent, D. E. Rozane, D. A. Amorim, A. Hernandes and W. Natale, “Unbiased Approach to Diagnose the Nutrient Status of Guava,” Proceedings of the 3rd International Symposium on Guava and Other Myrtaceae, Acta Horticulturae, Vol. 959, 2012, pp. 145- 159.
- J. J. Egozcue and V. Pawlowsky-Glahn, “Groups of Parts and Their Balances in Compositional Data Analysis,” Mathematical Geology, Vol. 37, No. 7, 2005, pp. 795- 828. http://dx.doi.org/10.1007/s11004-005-7381-9
- V. Pawlowsky-Glahn, J. J. Egozcue and R. TolosanaDelgado, “Principal Balances,” In: 4th International Workshop on Compositional Data Analysis (Codawork 2011), San Feliu de Guixols, Spain, 2011.
- G. De Rijk and E. Schrevens, “Distribution of Nutrients and Water in Rockwool Slabs,” Scientia Horticulturae, Vol. 72, No. 3-4, 1998, pp. 277-285. http://dx.doi.org/10.1016/S0304-4238(97)00144-1
- I. Loladze and J. J. Elser, “The Origins of the Redfield Nitrogen-to-Phosphorus Ratio Are in a Homoeostatic Protein-to-rRNA Ratio,” Ecology Letters, Vol. 14, No. 3, 2011, pp. 244-250. http://dx.doi.org/10.1111/j.1461-0248.2010.01577.x
- J. B. Jones Jr. and V. W. Case, “Sampling, Handling, and Analyzing Plant Tissue Samples,” In: R. L. Westerman, Ed., Soil Testing and Plant Analysis, Book Series 3, Soil Science Society of America, Madison, 1990, pp. 389-427.
- R Development Core Team, “R: A Language and Environment for Statistical Computing,” R. T. D. Core, Ed., R Foundation for Statistical Computing, Vienna, 2013.
- K. G. van den Boogaart, R. Tolosana-Delgado and M. Bren, “‘Compositions’: Compositional Data Analysis in R Package,” 2013. http://cran.rproject.org/package=compositions
- P. Filzmoser and M. Gschwandtner, “‘Mvoutlier’: Multivariate Outlier Detection Based on Robust Methods,” CRAN Repository, Vienna, 2013.
- J. Daunis-i-Estadella, C. Barceló-Vidal, C. and A. Buccianti, “Exploratory Compositional Data Analysis,” In: A. Buccianti, G. Mateu-Figueras and V. Pawlowsky-Glahn, Eds., Compositional Data Analysis in the Geosciences: From Theory to Practice, Geological Society, London, Special Publications 264, 2001, pp. 161-174.
- Z. Prekopcsák and L. Lemire, “Time Series Classification by Class-Specific Mahalanobis Distance Measures. Learning,” Advances in Data Analysis and Classification, Vol. 6, No. 3, 2012, pp. 185-200. http://dx.doi.org/10.1007/s11634-012-0110-6
- J. A. Swets, “Measuring the Accuracy of Diagnostic Systems,” Science, Vol. 240, No. 4857, 1988, pp. 1285-1293. http://dx.doi.org/10.1126/science.3287615
- W. J. Youden, “Index for Rating Diagnostic Tests,” Cancer, Vol. 3, No. 1, 1950, pp. 32-35. http://dx.doi.org/10.1002/1097-0142(1950)3:1<32::AID-CNCR2820030106>3.0.CO;2-3
- M. E. Sumner, “Effect of Corn Leaf Sampled on N, P, K, Ca and Mg Content and Calculated DRIS Indices,” Communications in Soil Science and Plant Analysis, Vol. 8, No. 3, 1977, pp. 269-280. http://dx.doi.org/10.1080/00103627709366719
- A. M. O. Elwali, G. J. Gascho and M. E. Sumner, “DRIS Norms for 11 Nutrients in Corn Leaves,” Agronomy Journal, Vol. 77, No. 3, 1985, pp. 506-508. http://dx.doi.org/10.2134/agronj1985.00021962007700030032x
- T. D. Needham, J. A. Burger and R. G. Oderwald, “Relationship between Diagnosis and Recommendation Integrated System (DRIS) Optima and Foliar Nutrient Critical Levels,” Soil Science Society of America Journal, Vol. 54, No. 3, 1990, pp. 883-886. http://dx.doi.org/10.2136/sssaj1990.03615995005400030045x
- P. N. Soltanpour, M. J. Malakouti and A. Ronaghi, “Comparison of Diagnosis and Recommendation Integrated System and Nutrient Sufficiency Range for Corn,” Soil Science Society of America Journal, Vol. 59, No. 1, 1995, pp. 133-139. http://dx.doi.org/10.2136/sssaj1995.03615995005900010021x
- K. Singh, H. S. Hundal and D. Singh, “Monitoring Nutrient Status for Maize in Northwestern India through Diagnosis and Recommendation Integrated System Approach,” Communications in Soil Science and Plant Analysis, Vol. 43, No. 22, 2012, pp. 2915-2923. http://dx.doi.org/10.1080/00103624.2012.728267
- A. C. D. Rocha, W. M. Leandro, A. O. Rocha, J. D. G. Santana and J. W. D. S. Andrade, “DRIS Norms for Corn Planted in Reduced Row Spacing in Hidrolândia, State of Goias, Brazil,” Bioscience Journal, Vol. 23, No. 4, 2007, pp. 50-60.
- G. D. Dagbenonbakin, A. K. Srivastava, T. Gaiser and H. Glodbach, “Maize Nutrient Assessment in Benin Republic: Case of Upper Ouémé Catchment,” Journal of Plant Nutrition, Vol. 36, No. 4, 2013, pp. 587-606. http://dx.doi.org/10.1080/01904167.2012.754031
- S. T. Dara, P. E. Fixen and R. H. Gerlderman, “Sufficiency Level and Diagnosis and Recommendation Integrated System Approaches for Evaluating the Nitrogen Status of Corn,” Agronomy Journal, Vol. 84, No. 6, 1992, pp. 1006-1010. http://dx.doi.org/10.2134/agronj1992.00021962008400060020x
- C. R. Escano, C. A. Jones and G. Uehara, “Nutrient Diagnosis in Corn Grown on Hydric Dystradepts: II. Comparison of Two Systems of Tissue Diagnosis,” Soil Science Society of America Journal, Vol. 45, No. 6, 1981, pp. 1140-1144. http://dx.doi.org/10.2136/sssaj1981.03615995004500060026x
- H. Delacour, A. Servonnet, A. Perrot, J. F. Virgezzi and J. M. Ramirez, “La Courbe ROC (Receiver Operating Characteristic): Principes et Principales Applications en Biologie Clinique,” Annales de Biologie Clinique, Vol. 63, No. 2, 2005, pp. 145-154.
- R. Beverly, “Comparison of DRIS and Alternative Diagnostic Methods for Soybean,” Journal of Plant Nutrition, Vol. 1, No. 8, 1987, pp. 901-920. http://dx.doi.org/10.1080/01904168709363619
- L. E. Parent, W. Natale and N. Ziadi, “Compositional Nutrient Diagnosis of Corn Using the Mahalanobis Distance as Nutrient Imbalance Index,” Canadian Journal of Soil Science, Vol. 89, No. 4, 2009, pp. 383-390. http://dx.doi.org/10.4141/cjss08050
- S. Güsewwell, “N:P Ratios in Terrestrial Plants: Variation and Functional Significance,” New Phytologist, Vol. 164, No. 2, 2004, pp. 243-266. http://dx.doi.org/10.1111/j.1469-8137.2004.01192.x
- C. Bould, “Leaf Analysis as a Diagnostic Method and Advisory Aid in Crop Production,” Experimental Agriculture, Vol. 4, No. 1, 1968, pp. 17-27. http://dx.doi.org/10.1017/S0014479700022316
Abbreviations
Acc.: accuracy;
AUC: area under curve;
CND: Compositional Nutrient Diagnosis;
DRIS: Diagnosis and Recommendation Integrated System;
FN: false negative;
FP: false positive;
NPV: negative predictive value;
PPV: positive predictive value;
ROC: receiving operating characteristic;
TN: true negative;
TP: true positive.
NOTES
*Corresponding author.

