Computational Water, Energy, and Environmental Engineering
Vol.06 No.01(2017), Article ID:73580,22 pages
10.4236/cweee.2017.61009
Prediction of Salinity Variations in a Tidal Estuary Using Artificial Neural Network and Three-Dimensional Hydrodynamic Models
Weibo Chen1, Wencheng Liu2*, Weiche Huang2,3, Hongming Liu2
1National Science and Technology Center for Disaster Reduction, Taiwan
2Department of Civil and Disaster Prevention Engineering, National United University, Taiwan
3Ph.D. Program in Materials and Chemical Engineering, National United University, Taiwan

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 21, 2016; Accepted: January 16, 2017; Published: January 19, 2017
ABSTRACT
The simulation of salinity at different locations of a tidal river using physically-based hydrodynamic models is quite cumbersome because it requires many types of data, such as hydrological and hydraulic time series at boundaries, river geometry, and adjusted coefficients. Therefore, an artificial neural network (ANN) technique using a back-propagation neural network (BPNN) and a radial basis function neural network (RBFNN) is adopted as an effective alternative in salinity simulation studies. The present study focuses on comparing the performance of BPNN, RBFNN, and three-dimensional hydrodynamic models as applied to a tidal estuarine system. The observed salinity data sets collected from 18 to 22 May, 16 to 22 October, and 26 to 30 October 2002 (totaling 4320 data points) were used for BPNN and RBFNN model training and for hydrodynamic model calibration. The data sets collected from 30 May to 2 June and 11 to 15 November 2002 (totaling 2592 data points) were adopted for BPNN and RBFNN model verification and for hydrodynamic model verification. The results revealed that the ANN (BPNN and RBFNN) models were capable of predicting the nonlinear time series behavior of salinity to the multiple forcing signals of water stages at different stations and freshwater input at upstream boundaries. The salinity predicted by the ANN models was better than that predicted by the physically based hydrodynamic model. This study suggests that BPNN and RBFNN models are easy-to-use modeling tools for simulating the salinity variation in a tidal estuarine system.
Keywords:
Salinity Variation, Artificial Neural Network, Backpropagation Algorithm, Radial Basis Function Neural Network, Three-Dimensional Hydrodynamic Model, Tidal Estuary

1. Introduction
Estuaries act as a bridge between riverine and marine systems, transporting dissolved substances and suspended particles from rivers to coastal seas. In the past decades, coastal environments have become more stressed by pollutants introduced from the surrounding land. The fates of pollutants are strongly affected by physical processes, which interplay with biogeochemical processes in estuaries [1] . Salinity is an important indicator of the health of the aquatic ecosystem in tidal estuaries. The increase in salinity intrusion in a tidal estuary river may have an adverse effect on the drinking-water supply and aquatic environment [2] .
Numerical models have been successfully applied to the simulation of the hydrodynamic characteristics of estuaries. Although full three-dimensional models are available to predict salt water intrusion in an estuary, a large amount of observational data and a considerable amount of effort are often needed to calibrate and validate these numerical models for further applications [3] - [14] . Because of the existing difficulties and challenges in the prediction of salinity variations using hydrodynamic model, a relatively novel computational approach, artificial neural networks (ANNs), which was widely accepted in many disciplines, provides an alternative method for one-step-ahead understanding and management of hydrodynamic processes. ANNs are well-suited for this application because of their informative processing characteristics, such as nonlinearity, parallelism, noise tolerance, and learning capability [15] [16] .
ANNs are a branch of artificial intelligence developed in the 1950s that aims at imitating the biological brain architecture. They are parallel-distributed systems made of many interconnected nonlinear processing elements, called neurons [17] . Renewed interest in ANNs has developed in the last decade, mainly because of the availability of suitable hardware (e.g., parallel computers, analogue/digital neural cards for personal computers) that has made them convenient for fast data analysis and information processing.
ANNs are now drawing interest from researchers in various fields because they are capable of providing a neurocomputing approach for solving complex problems that might otherwise not have a tractable solution. ANNs have been applied to a broad range of fields including nonlinear system modeling, function approximation, pattern recognition and synthesis, and prediction. An ANN is a nonlinear mathematical structure that is able to represent arbitrarily complex nonlinear processes that relate the inputs and outputs of any system. One needs to train the network through representative examples of the desired mapping. The ANN can then adapt itself to reproduce the desired output when presented with training input. This means that the network has the ability to learn (i.e., to extract import features) from the data and to generalize for future classification or prediction. Recently, ANNs have provided a significant number of promising results in the field of hydrology and water resources, in areas such as rainfall estimation [18] - [30] , groundwater modeling [31] [32] [33] [34] [35] , estuary water- stage forecasting [36] [37] [38] [39] , and reservoir operation [40] [41] [42] . Although the neural networks applied to different hydrological processes have yielded many exciting results, this method is still rarely applied in modeling the salinity distributions of tidal estuaries [43] or compared with predictions of salinity obtained using a hydrodynamic model [44] .
The main aim of this paper was to implement two ANN models which are a back- propagation neural network (BPNN) and a radial basis function neural network (RBFNN) and a physically based three-dimensional hydrodynamic model to predict the time-series salinity variation in response to the input forcing functions of the water stage and freshwater discharge in the Danshui River estuary of northern Taiwan.
2. Description of Study Site
The Danshui River estuarine system (Figure 1) is the largest estuary in Taiwan. There are three main tributaries including the Dahan River, the Xindian River, and the Keelung River. Its drainage basin covers the capital city of Taipei. The watershed of the Danshui River encompasses 2726 km2 and has a combined length of 158.7 km. Annual precipitation in the region ranges between 1500 mm and 2500 mm, with the majority coming in late spring (May) to early fall (October). Long-term average annual river flow rate is 6.6 × 109 m3/y. Except during a flood event, the astronomical tide may reach as far upriver as the Chenglin Bridge on the Dahan River, the Xiulang Bridge on the Xindian River, and the Jiangbei Bridge on the Keelung River. Tidal propagation is the dominant mechanism controlling the water surface elevation and the ebb and flood flows. The M2 tide is the primary tide constituent at the river mouth, with a tidal range of 2.17 m at mean tide and up to 3 m at spring tide [45] . Seawater intrudes upriver as a result of tidal advection and two-layer estuarine circulation. Salinity varies on an intratidal time scale in response to the ebb and flood of the flows and in various longer time scales in response to freshwater inflow. The limit of salt intrusion may reach beyond 25 km in the Dahan River from the river mouth during the period of low flow.
The average river discharges at the upstream limits of the tide are 63.1 m3/s, 72.7
Figure 1. A map of the Danshui River estuarine system.
m3/s, and 26.1 m3/s, respectively, in the Dahan River, the Xindian River, and the Keelung River. Due to the shallowness of the estuary, it is well mixed in most areas with the exception for a short section near Guandu Bridge (Figure 1), where the channel depth reaches 13 m and two-layer circulation occurs [46] .
3. Materials and Methods
3.1. Artificial Neural Networks
A neural network consists of a large number of simple processing elements that are called neurons and nodes. Each neuron is connected to other neurons by means of direct communication links, each with an associated weight. The weights represent information being used by the net to solve a problem. An input layer, a hidden layer where the elaborations are performed, and an output layer constitute the most commonly used perceptron, called a single-hidden-layer perceptron. The single unit of the network, i.e., the model neuron, is shown in Figure 2. Neural networks can be classified into many types based on their structures. In the current study, a back-propagation neural network (BPNN) and a radial basis function neural network (RBFNN) were chosen to establish the present model.
3.2. Back-Propagation Neural Networks (BPNNs)
The BPNN proposed by Rumelhart et al. [47] is widely used among all of the ANNs. It is a multiple-layer network with nonlinear differentiable transfer functions. It can be used to solve many nonlinear problems. The input vectors and its corresponding target vectors are used to train a BPNN until it can approximate a specified minimum error or maximum epochs. A BPNN with weightings, biases, a sigmoid layer, and a linear output layer has the capacity to approximate any function with a finite number of discontinuities [48] .
Figure 2 presents the architecture of a BPNN. It shows that Pi is the input vector; IW and b1 are the weights and biases, respectively, between the input layer and the hidden layer; Trans. is the transfer function, and LW and b2 are the weights and biases, respectively, between the hidden layer and the output layer. We use sigmoid transfer functions in the hidden layer and linear transfer functions in the output layer to extrapolate beyond the range of the training data. Detailed equations to describe the connections between input and hidden-layer neurons and those between hidden and output-layer neurons can be found in Chen et al. [37] and will not be further described here.
Kisi [49] reported that the Levenberg-Marquardt technique [50] is more powerful than the conventional gradient descent techniques [51] [52] to find the weight and the
Figure 2. The architecture of the back-propagation neural network.
bias matrices in each iteration. Therefore the Levenberg-Marquardt algorithm was adopted in BPNNs. The toolbox of neural network includes the Levenberg-Marquardt technique which is incorporated into the ANN model to be executed in the Matlab environment.
3.3. Radial Basis Function Neural Network (RBFNN)
RBFNN, which is multilayer and feedforward, is often used for strict interpolation in multidimensional space. The term “feedforward” means that the neurons are organized in the form of layers in a layered neural network [53] . In the present study, the architecture of RBFNN consists of three layers: an input layer, a single hidden layer, and an output layer. Figure 3 shows the architecture of the RBFNN. The input layer is composed of input nodes. The only hidden layer consists of locally tuned units, and each unit has a radial basis function acting as a hidden node. The output of the RBFNN can be calculated according to Equation (1).
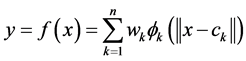 (1)
(1)
where x is the input vector, 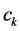 is the center of the radial basis function for hidden layer n,
is the center of the radial basis function for hidden layer n, 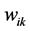 are the weights in the output layer, and
are the weights in the output layer, and 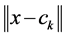 denotes the Euclidean distance between the center of the radial basis function and the input. Two functions, multiquadratic function and Gaussian activation function, are the most commonly used for radial basis function. A range of studies have indicated that the results are insensitive to different basis functions [54] [55] . In this study, the radial basis function
denotes the Euclidean distance between the center of the radial basis function and the input. Two functions, multiquadratic function and Gaussian activation function, are the most commonly used for radial basis function. A range of studies have indicated that the results are insensitive to different basis functions [54] [55] . In this study, the radial basis function 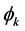 is chosen as the multiquadratic function and defined in Equation (2).
is chosen as the multiquadratic function and defined in Equation (2).
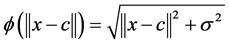 (2)
(2)
where σ is the standard deviation and c is the center of the multiquadratic function.
A main challenge in the design of RBFNN is the selection of centers. The simplest way to select the centers of RBFNN is random method [56] . However, the orthogonal least squares (OLS) algorithm can provide an optimum number of centers in RBFNN from the training patterns [57] . The classical Gram-Schmidt and modified Gram- Schmidt methods [58] can be used to deal with orthogonalization procedure [59] . The OLS method based on classical Gram-Schmidt offers a systematic way for center selection
Figure 3. The architecture of the radial basis function neural network.
and significantly reduces the size of the RBFNN.
The OLS learning algorithm is a procedure that iteratively selects the best regressors (radial basis unit) from a set of available regressors. This set is composed of a number of regressors equal to the number of available data, and each regressor is a radial unit centered on a data point. The OLS algorithm proceeds iteratively by selecting the next best regressor from a set by applying a Gram-Schmidt orthogonalization until reaching the tolerance, so the contribution of each vector of this new orthogonal base can be determined individually among the available regressors. A detailed description of the algorithm can be found in Ham & Kostanic [60] .
3.4. Three-Dimensional Hydrodynamic Model
The ELCRIC (Eulerian-Lagrangian CIRCulation) model is used for simulating salinity in a tidal estuary, because this model is cost efficiency to prevent the time step constraints and the unstructured grid can be used to fit the complex coastline and channel. The model solves the shallow water equations using a semi-implicit Eulerian-Lagran- gian finite volume/finite difference method that relies on horizontally unstructured grids and unstretched z-coordinates. ELCIRC allows for the use of state-of-the-art turbulence closure schemes, includes terms for the tidal potential and atmospheric pressure gradients, and provides a detailed description of air-water exchanges.
The model solves for the free surface elevation, three-dimensional water velocity, and salinity using hydrostatic equations based on the Boussinesq approximation, which represents mass conservation, momentum conservation, and conservation of salt:
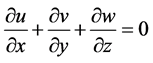 (3)
(3)
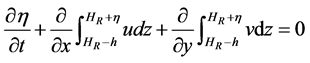 (4)
(4)
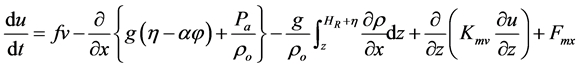 (5)
(5)
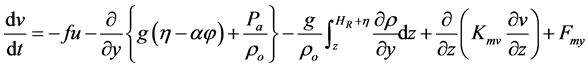 (6)
(6)
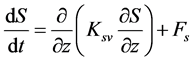 (7)
(7)
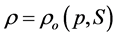 (8)
(8)
where 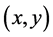 are the horizontal Cartesian coordinates;
are the horizontal Cartesian coordinates; 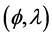 are the latitude and longitude; z is the vertical coordinate, positive upward; t is time;
are the latitude and longitude; z is the vertical coordinate, positive upward; t is time;  is the z-coordinate at the reference level (mean sea level);
is the z-coordinate at the reference level (mean sea level); 












In ELCRIC, the barotropic pressure gradient in the momentum equation and the flux term in the continuity equation are treated semi-implicitly, with the implicitness factor
4. Results and Discussion
There are many indices to assess the model performance between model prediction and observational data. In this study, we used the commonly acceptable indices to evaluate the performances of the BPNN, RBFNN, and three-dimensional hydrodynamic models, including the root mean square error (RMSE), mean absolute error (MAE), and correlation coefficient (CC) to calculate the accuracy of the model prediction.



where 

simulated salinity; and So is the measured salinity.
4.1. BPNN Model Training and Verification
The measured data of hourly salinity at 0.5 m depth below the water surface at the Guandu Bridge were collected and adopted for training and verification phases with the ANN models (BPNN and RBFNN) and for model calibration and verification with the three-dimensional hydrodynamic model. The data sets collected from 18 to 22 May, 16 to 22 October, and 26 to 30 October 2002 (totaling 4320 data points) were used for BPNN and RBFNN model training and for hydrodynamic model calibration. The data sets collected from 30 May to 2 June and 11 to 15 November 2002 (totaling 2592 data points) were applied for BPNN and RBFNN model verification and for hydrodynamic model verification. Those historical data of 2002 were continuously measured data at the Guandu Bridge station to be taken in this study. Some measured data in the Danshui River estuarine system can not be adopted for model calibration and verification because the data sets are not continuous.
For a given input set, the BPNN produces an output, and this response is compared with the known desired response of each neuron. The weights of the neural network are then changed to correct or reduce the error between the output of the neuron and the desired response, and this process continues. The weights are continually changed until the total error of all training sets is reduced below the accepted error.
This study builds a BPNN model to simulate estuary salinity at the Guandu Bridge station. The BPNN used in this study is composed of three layers with nodes in adjacent layers fully connected. This is, only one hidden layer is employed. Because the focus is on single variable predicting, one output node is exclusively used in the output layer. The number of input nodes and the number of hidden nodes are the two major experimental factors.
Figure 4 illustrates the structure of the BPNN model for salinity prediction. The input units include time-series water stages and freshwater discharges at different stations. The hourly water stages at the observed stations include the Danshui River mouth, Taipei Bridge, and Dazhi Bridge, while the upstream reaches of the Dahan River, Xindian River, and Keelung River are specified with hourly freshwater discharges. Figure 5 and Figure 6 present the time-series freshwater discharges in the Dahan River, Xindian River, and Keelung River and the time-series hourly water stages at the Danshui River mouth, respectively.
With different combinations of the number of hidden layers and the number of hidden neurons, the BPNN model was trained until the best architecture was obtained. The Mean Square Error (MSE) criterion was used to evaluate the performance of the model during the training phase. Satisfactory results were obtained using only one hidden layer with seven neurons. To prevent overtraining the model, this study chose a learning rate of 0.01 and a momentum of 0.3. Therefore, the architecture of 6-7-1 (i.e., input neurons, hidden neurons, and output neurons) was chosen as the best BPNN
Figure 4. The structure of the BPNN model used for salinity prediction.
Figure 5. Upstream freshwater discharges in the Dahan River (solid line), Xindian River (dashed line), and Keelung River (dotted-dashed line) used for the (a) training (calibration) and (b) verification phases.
Figure 6. Time-series water stages at the Danshui River mouth used for the (a) train- ing (calibration) and (b) verification phases.
architecture, which was then tested using the data sets from the year 2002. The comparison between observed salinities and BPNN predicted salinities at the Guandu Bridge during the training and verification phases is presented in Figure 7. It should be noted that the errors between the predicted and observed salinities are also shown in the figure. The BPNN model during the training and verification phases was found to underestimate the peak during flood tide and to over predict minimal salinities during ebb tide. The RMSE, MAE, and CC during the training phase were found to be 3.88 ppt, 2.79 ppt, and 0.76, respectively, while during the verification phase they are 3.81 ppt, 2.96 ppt, and 0.71, as shown in Table 1.
4.2. RBFNN Model Training and Verification
The RBFNN methodology has the advantage that hidden weights or center vectors are optimized first before they are forwarded to the output layer. Hidden-output layer weights are further optimized using the Orthogonal Least Squares (OLS) method. Therefore, there was no backflow at the input-hidden layer, which reduces the simulating time. The best RBFNN architecture (i.e., number of center vectors in the hidden layers) was obtained by trial and error based on the mean square error in the training and verification phases. The architecture of 6-16-1 (i.e., input neurons, hidden neurons,

Figure 7. Comparison of the temporal variation of the observed and predicted salinities at the Guandu Bridge during the (a) training and (b) verification phases for the BPNN model. Note that circles are observations and the solid line represents the BPNN modeling results.
Table 1. The performances of BPNN, RBFNN and three-dimensional models in salinity simulation.
Note: RMSE represents root mean square error; MAE represents mean absolute error; CC represents correlation coefficient.
and output neurons) was chosen as the best RBFNN architecture. In this study, we set 0.9 as the tolerance of the OLS algorithm, and 16 center vectors were selected after the OLS algorithm was completed.
Figure 8 presents a comparison of the salinity predicted by the RBFNN model during the training and verification phases and that observed at the Guandu Bridge. During the training and verification phases, the RBFNN model underestimated the peak during flood tides and over predicted the minimal salinities during ebb tides. The RMSE, MAE, and CC during the training phase were found to be 3.76 ppt, 2.72 ppt, and 0.77, respectively, while during the verification phase, they were 3.63 ppt, 2.90 ppt, and 0.75, as shown in Table 1.
Figure 8. Comparison of the temporal variation of observed and predicted salinities at the Guandu Bridge during the (a) training and (b) verification phases for the RBFNN model. Note that circles are observation and the solid line represents the RBFNN modeling results.
4.3. Calibration and Verification of the Three-Dimensional Hydrodynamic Model
Bottom topography is an important factor that affects the flow properties in environmental modeling. The bottom topography data in the coastal sea and Danshui River estuarine system (Figure 9(a)) were obtained from the National Center for Ocean Research and Water Resources Agency, Taiwan. The greatest depth in the study area is 110 m (below mean sea level) near the northeast corner of the model in the coastal sea. The model mesh for the Danshui River estuarine system and its adjacent coastal sea
Figure 9. (a) Bathymetry contour map of the Danshui River estuarine system and (b) an unstructured grid representing the modeling domain.
consisted of 6969 polygons (Figure 9(b)). To save computational time, higher-resolu- tion grids were used in the Danshui River estuary, and coarser grids were used in the coastal sea. Because the model domain includes deep bathymetry in the coastal ocean and a shallow area in the channel, thirty-two levels varying in thickness from 1 to 10 m were used for vertical discretization in ELCIRC. The time step (
The model calibration and verification of salinity was conducted using daily freshwater discharge values from upriver regions of the Dahan River, the Xindian River, and the Keelung River in 2002 (shown in Figure 5). A five-constituent tide (i.e., M2, S2, N2, K1, and O1) was adopted as the forcing function at the coastal sea boundaries. The salinities at the open boundaries with the coastal sea were set to 35 ppt. Salinity values at the upstream boundaries of the three tributaries were set to zero due to freshwater discharge from the boundaries.
Before the model was calibrated and verified with measured salinity variations, the model was performed to compare with the measured tidal level and tidal current at the Guandu Bridge (shown in Figure 1). The results indicate that MAE and RMSE values between the measured hourly water surface elevations and the computed results are 0.21 m and 0.30 m, respectively, for model calibration, while MAE and RMSE values are 0.28 m and 0.34 m, respectively, for model verification. An intensive survey of the tidal current was conducted at transect of the Guandu Bridge on April 26, 2002. The current was measured by trained technicians on boats every half hour for a period of 13 daylight hours. The measured longitudinal velocities were used to validate the model. The MAE and RMSE values at the Guandu Bridge are 0.156 m/s and 0.188 m/s, respectively. We found that the model was satisfactorily validated with water surface elevation and tidal current. Finally, the constant bottom roughness height (zo = 0.005 m) was adopted in the model simulation.
The model was then performed to compare with the measured salinity variation at the Guandu Bridge. Figure 10 illustrates the model calibration and verification results for the salinity from the three-dimensional hydrodynamic model. The lower salinity conditions were over predicted, whereas the higher salinity values were underpredicted for the model calibration and verification. The RMSE, MAE, and CC for the model calibration were found to be 4.49 ppt, 3.80 ppt, and 0.79, respectively, while for the model verification, they were 5.09 ppt, 4.25 ppt, and 0.75, as shown in Table 1.
4.4. Comparison of Predicted Results Using ANN and Three-Dimensional Hydrodynamic Models
During the comparison of the results, terminologies such as training and verification of the ANN (BPNN and RBFNN) approaches were considered analogous to calibration and verification of the three-dimensional hydrodynamic model, respectively. According to the performance different approaches, one month of simulation using a three-dimen- sional hydrodynamic model requires approximately 2.5 hours of Central Processing Unit (CPU) time on an Intel Core I5 Personal Computer (PC), while the ANN (BPNN and RBFNN) models require only 3 minutes. To assess the relative performance of the models in predicting the salinity, values of performance indices obtained from
Figure 10. Comparison of the temporal variation of the observed and predicted salinities at the Guandu Bridge for the three-dimensional hydrodynamic model (a) calibration and (b) verification. Note that circles are observations and the solid line represents the modeling results.
the BPNN, RBFNN, and three-dimensional hydrodynamic models were compared. The performance indices of the BPNN and RBFNN models yielded during the training phase were compared with the corresponding performance indices yielded during the three-dimensional hydrodynamic model calibration. The RMSE, MAE, and CC obtained from the best BPNN and RBFNN architectures were compared with calibration results obtained using the three-dimensional hydrodynamic model. Similarly, the verification results of the BPNN and REFNN models were compared with the verification results of the three-dimensional hydrodynamic model.
Figure 11 presents the scatter plots of the comparisons between the measured and predicted salinity with BPNN, RBFNN, and three-dimensional hydrodynamic models. The BPNN and RBFNN predicted salinities were noted to be distributed uniformly
Figure 11. Scatter plots of observations versus predictions using the (a), (b) BPNN model, (c), (d) RBFNN model, and (e), (f) three-di- mensional hydrodynamic model.
about the best-fit line. The performance of the BPNN and RBFNN was better than that of the three-dimensional hydrodynamic model during the training and verification phases, as revealed by the values of the RMSE and MAE. There are small differences in the CC value with the three predicted models. However, all CC values are above 0.70, as shown in Table 1. According to the values of RMSE and MAE, the RBFNN was found to be better than the BPNN. However, the results show that the ANN (BPNN and RBFNN) approach is capable of reproducing the nonlinear relationship between the input and output. Although the ANN models may predict the salinity variations, the limitation of the ANN models is that they are black box models that fail to simulate the internal physical processes in a tidal estuary. The three-dimensional hydrodynamic model is a physically based model that can be adopted to simulate salinity variations at different layers (i.e. vertical profile) and locations.
The simulation of physical processes is crucial importance to environmental management. Engineering alterations to the estuaries may change the salinity distribution, resulting in negative effects on the estuarine ecosystems [64] [65] . Three-dimensional hydrodynamic models have been widely implemented to provide detailed resolutions as a result of engineering alterations, however a large amount of observational data and a considerable amount of effort are necessary to calibrate and validate the models before these models are applied for prediction. Therefore, ANN models which are the data-driven approaches would be useful for engineers to make rapid evaluation of salinity changes due to the modifications in the tidal estuaries [43] [44] .
5. Conclusions
Salinity is an important indicator of the health of the aquatic ecosystem in tidal estuaries. In the present study, estuarine salinities were predicted using ANN (BPNN and RBFNN) and three-dimensional hydrodynamic models. The driven forcing functions of the ANN models include the time-series water stages and the freshwater discharges at different stations, which served as input. Although the BPNN and RBFNN approaches are black-box models, the results revealed that the salinity values predicted by the BPNN and RBFNN models are better than those predicted by the three-dimensional hydrodynamic model. Because the ANN approach is a data-driven technique, the predictability could be further improved by providing an appropriate and large number of input-output data sets during training.
In the present study, we focus on the salinity prediction instead of forecasting. In future study, different lead-time forecast in salinity variations can be developed for environmental management. The soft computing techniques such as the combining fuzzy optimal model with a genetic programming [66] , neural network and genetic programming [67] , support vector machine [68] [69] , dendrochronlogy [70] , hybrid neural network [71] , and binary-coded particle swarm optimization and extreme learning machines [72] can also be developed to improve the prediction of salinity distributions along the tidal estuary.
Acknowledgements
This study is financially supported, in part, by the Ministry of Science and Technology (MOST), Taiwan under grant No. 104-2625-M-239-002. The authors would like to appreciate the Taiwan Water Resources Agency and Industrial Technology Research Institute for providing the observational data.
Cite this paper
Chen, W.B., Liu, W.C., Huang, W.C. and Liu, H.M. (2017) Prediction of Salinity Variations in a Tidal Estuary Using Artificial Neural Network and Three-Dimensional Hydrodynamic Models. Computational Water, Energy, and Environmental Engineering, 6, 107-128. http://dx.doi.org/10.4236/cweee.2017.61009
References
- 1. Lin, J., Xie, L., Pietrafesa, L.J., Ramus, J.S. and Paerl, H.W. (2007) Water Quality Gradients across Albemarle-Pamlico Estuarine System: Seasonal Variations and Model Applications. Journal of Coastal Research, 23, 213-229.
https://doi.org/10.2112/05-0507.1 - 2. Bhuiyan, M.J.A.N., and Dutta, D. (2012) Assessing Impact of Sea Level Rise on River Salinity in the Goari River Network, Bangladesh. Estuarine, Coastal and Shelf Science, 96, 219-227.
https://doi.org/10.1016/j.ecss.2011.11.005 - 3. Ahsan, Q., Blumberg, A.F., Thuman, A.J. and Gallagher, T.W. (2005) Geomorphological and Meteorological Control of Estuarine Processes: A Three-Dimensional Modeling Analysis. Journal of Hydraulic Engineering, ASCE, 131, 259-272.
https://doi.org/10.1061/(ASCE)0733-9429(2005)131:4(259) - 4. Mao, X., Jiang, W., Zhao, P. and Gao, H. (2008) A 3-D Numerical Study of Salinity Variations in the Bohai Sea during the Recent Years. Continental Shelf Research, 28, 2689-2699.
https://doi.org/10.1016/j.csr.2008.09.004 - 5. Zhang, Y.L. and Baptista, A.M. (2008) SELFE: A Semi-Implicit Eulerian-Lagrangian Finite-Element Model for Cross-Scale Ocean Circulation. Ocean Modelling, 21, 71-96.
https://doi.org/10.1016/j.ocemod.2007.11.005 - 6. Xue, P., Chen, C., Ding, P., Beardsley, R.C., Lin, H., Ge, J. and Kong, Y. (2009) Salt Water Intrusion into the Changjiang River: A Model-Guided Mechanism Study. Journal of Geophysical Research, 114, C02006.
https://doi.org/10.1029/2008jc004831 - 7. Huang, W. (2010) Hydrodynamic Modeling and Ecohydrological Analysis of River Inflow Effects on Apalachicola Bay, Florida, USA. Estuarine, Coastal and Shelf Science, 86, 526-534.
https://doi.org/10.1016/j.ecss.2009.07.032 - 8. Chen, X. (2012) A Sensitivity Analysis of Low Salinity Habitats Simulated by a Hydrodynamic Model in the Manatee River Estuary in Florida, USA. Estuarine, Coastal and Shelf Science, 104-105, 80-90.
https://doi.org/10.1016/j.ecss.2012.03.023 - 9. Rice, K.C., Hong, B. and Shen, J. (2012) Assessment of Salinity Intrusion in the James and Chickahominy Rivers as a Result of Simulated Sea-Level Rise in Chesapeake Bay, East Coast, USA. Journal of Environmental Management, 111, 61-69.
https://doi.org/10.1016/j.jenvman.2012.06.036 - 10. Chua, V.P. (2013) Modeling the Variations of Freshwater Inflows and Tidal Mixing on Estuarine Circulation and Salt Flux. Journal of Coastal Research, 28, 1391-1399.
https://doi.org/10.2112/JCOASTRES-D-12-00143.1 - 11. Gong, W., Shen, J. and Jia, L. (2013) Salt Intrusion during the Dry Season in the Huang-maohai Estuary, Pearl River Delta, China. Journal of Marine Systems, 111-112, 235-252.
https://doi.org/10.1016/j.jmarsys.2012.11.006 - 12. Chen, W.B., Liu, W.C. and Hsu, M.H. (2015) Modeling Assessment of a Saltwater Intrusion and a Transport Time Scale Response to Sea-Level Rise in a Tidal Estuary. Environmental Fluid Mechanics, 15, 491-514.
https://doi.org/10.1007/s10652-014-9367-y - 13. Chen, W., Chen, K., Kuang, C., Zhu, D.Z., He, L., Mao, X., Liang, H. and Song, H. (2016) Influence of Sea Level Rise on Saline Water Intrusion in the Yangtze River Estuary, China. Applied Ocean Research, 54, 12-25.
https://doi.org/10.1016/j.apor.2015.11.002 - 14. Karna, T. and Baptista, A.M. (2016) Evaluation of a Long-Term Hindcast Simulation for the Columbia River Estuary. Ocean Modelling, 99, 1-14.
https://doi.org/10.1016/j.ocemod.2015.12.007 - 15. Hagan M. T., Demuth, H. and Beale, M. (1995) Neural Network Design. PWS Publishing Company, Boston.
- 16. Wu, C.L., Chau, K.W. and Li, Y.S. (2009) Method to Improve Neural Network Performance in Daily Flows Prediction. Journal of Hydrology, 372, 80-93.
https://doi.org/10.1016/j.jhydrol.2009.03.038 - 17. Hecht-Nielsen, R. (1990) Neurocomputing. Addison-Wesley, Boston.
- 18. Chattopadhyay, S. (2007) Feed forward Artificial Neural Network Model to Predict the Average Summer-Monsoon Rainfall in India. Acta Geophysica, 55, 369-382.
https://doi.org/10.2478/s11600-007-0020-8 - 19. Guhathakurta, P. (2008) Long Lead Monsoon Rainfall Prediction for Meteorological Sub-Divisions of India Using Deterministic Artificial Neural Network Model. Meteorology and Atmospheric Physics, 101, 93-108.
https://doi.org/10.1007/s00703-008-0335-2 - 20. Hung, N.Q., Babel, M.S., Weesakul, S. and Tripathi, N.K. (2009) An Artificial Neural Network Model for Rainfall Forecasting in Bangkok, Thailand. Hydrology and Earth System Sciences, 23, 1413-1425.
https://doi.org/10.5194/hess-13-1413-2009 - 21. Wu, C.L. and Chau, K.W. (2011) Rainfall-Runoff Modeling Using Artificial Neural Network Coupled with Singular Spectrum Analysis. Journal of Hydrology, 399, 394-409.
https://doi.org/10.1016/j.jhydrol.2011.01.017 - 22. Wu, C.L. and Chau, K.W. (2002) Prediction of Rainfall Time Series Using Modular Soft Computing Methods. Engineering Applications of Artificial Intelligence, 26, 997-1007.
https://doi.org/10.1016/j.engappai.2012.05.023 - 23. Young, C.C. and Liu, W.C. (2015) Prediction and Modelling of Rainfall-Runoff during Typhoon Events Using a Physically-Based and Artificial Neural Network Hybrid Model. Hydrological Sciences Journal, 60, 2102-2116.
https://doi.org/10.1080/02626667.2014.959446 - 24. Ahmed, J.A. and Sarma, A.K. (2007) Artificial Neural Network Model for Synthetic Streamflow Generation. Water Resources Management, 21, 1015-1029.
https://doi.org/10.1007/s11269-006-9070-y - 25. Kisi, O. (2007) Streamflow Forecasting Using Different Artificial Neural Network Algorithms. Journal of Hydrolgic Engineering, ASCE, 12, 532-539.
https://doi.org/10.1061/(ASCE)1084-0699(2007)12:5(532) - 26. Chen, X., Wu, J. and Hu, Q. (2008) Simulation of Climate Change Impacts on Streamflow in the Bosten Lake Basin Using an Artificial Neural Network. Journal of Hydrologic Engineering, ASCE, 13, 180-183.
https://doi.org/10.1061/(ASCE)1084-0699(2008)13:3(180) - 27. Wang, W.C., Chau, K.W., Cheng, C.T. and Liu, Q. (2009) A Comparison of Performance of Several Artificial Intelligence Methods for Forecasting Monthly Discharge Time Series. Journal of Hydrology, 374, 294-306.
https://doi.org/10.1016/j.jhydrol.2009.06.019 - 28. Gao, C., Gemmer, M., Zheng, X.F., Liu, B., Su, D.B. and Wen, Y.H. (2010) Projected Streamflow in the Huaihe River Basin (2010-2100) Using Artificial Neural Network. Stochastic Environmental Research and Risk Assessment, 24, 685-697.
https://doi.org/10.1007/s00477-009-0355-6 - 29. Chau, K.W. and Wu, C.L. (2010) A Hybrid Model Coupled with Singular Spectrum Analysis for Daily Rainfall Prediction. Journal of Hydroinformatics, 12, 458-473.
https://doi.org/10.2166/hydro.2010.032 - 30. Can, I., Tosunoglu, F. and Kahya, E. (2012) Daily Streamflow Modelling Using Autoregressive Moving Average and Artificial Neural Networks Models: Case Study of Coruh Basin, Turkey. Water and Environment Journal, 26, 567-576.
https://doi.org/10.1111/j.1747-6593.2012.00337.x - 31. Purkait, B., Kadam, S.S. and Das, S.K. (2008) Application of Artificial Neural Network Model to Study Arsenic Contamination in Groundwater of Malda District, Eastern India. Journal of Environmental Informatics, 12, 140-149.
https://doi.org/10.3808/jei.200800132 - 32. Banerjee, P., Prasad, P.K. and Singh, V.S. (2009) Forecasting of Groundwater Level in Hard Rock Region Using Artificial Neural Network. Environmental Geology, 58, 1239-1246.
https://doi.org/10.1007/s00254-008-1619-z - 33. Mohanty, S., Jha, M.K., Kumar, A. and Sudheer, K.P. (2010) Artificial Neural Network Modeling for Groundwater Level Forecasting in a River Island of Eastern India. Water Resources Management, 24, 1845-1865.
https://doi.org/10.1007/s11269-009-9527-x - 34. Jalalkamali, A. and Jalalkamali, N. (2011) Groundwater Modeling Using Hybrid of Artificial Neural Network with Genetic Algorithm. African Journal of Agricultural Research, 6, 5775-5784.
https://doi.org/10.5897/ajar11.1892 - 35. Taormina, R., Chau, K.W. and Sethi, R. (2012) Artificial Neural Network Simulation of Hourly Groundwater Levels in a Coastal Aquifer System of the Venice Lagoon. Engineering Applications of Artificial Intelligence, 25, 1670-1676.
https://doi.org/10.1016/j.engappai.2012.02.009 - 36. Liang, S.X., Li, M.C. and Sun, Z.C. (2008) Prediction Models for Tidal Level Including Strong Meteorological Effects Using a Neural Network. Ocean Engineering, 35, 666-675.
https://doi.org/10.1016/j.oceaneng.2007.12.006 - 37. Chen, W.B., Liu, W.C. and Hsu, M. H. (2012) Comparison of ANN Approach with 2D and 3D Hydrodynamic Models for Simulating Estuary Water Stage. Advances in Engineering Software, 45, 69-79.
https://doi.org/10.1016/j.advengsoft.2011.09.018 - 38. Tsai, C.P. and You, C.Y. (2014) Development of Models for Maximum and Time Variation of Storm Surges at the Tanshui Estuary. Natural Hazards and Earth System Sciences, 14, 2313-2320.
https://doi.org/10.5194/nhess-14-2313-2014 - 39. Liu, W.C. and Chung, C.E. (2014) Enhancing the Predicting Accuracy of the Water Stage Using a Physical-Based Model and Artificial Neural Network-Genetic Algorithm in a River System. Water, 6, 1642-1661.
https://doi.org/10.3390/w6061642 - 40. Chang, Y.T., Chang, L.C. and Chang, F.J. (2005) Intelligent Control for Modeling of Real-Time Reservoir Operation. Part II: ANN with Operating Curves. Hydrological Processes, 19, 1431-1444.
https://doi.org/10.1002/hyp.5582 - 41. Deka, P.C. and Chandramouli, V. (2009) Fuzzy Neural Network Modeling of Reservoir Operation. Journal of Water Resources Planning and Management, ASCE, 135, 5-12.
https://doi.org/10.1061/(ASCE)0733-9496(2009)135:1(5) - 42. Wang, K.C., Chau, K.W., Xu, D.M. and Chen, X.Y. (2015) Improving Forecasting Accuracy of Annual Runoff Time Series Using ARIMA Based on EEMD Decomposition. Water Resources Management, 29, 2655-2675.
https://doi.org/10.1007/s11269-015-0962-6 - 43. Huang, W. and Foo, S. (2002) Neural Network Modeling of Salinity Variation in Apalachicola River. Water Research, 36, 356-362.
https://doi.org/10.1016/S0043-1354(01)00195-6 - 44. Adib, A. and Javdan, F. (2015) Interactive Approach for Determination of Salinity Concentration in Tidal River (Case Study: The Karun River in Iran). Ain Shams Engineering Journal, 6, 785-793.
https://doi.org/10.1016/j.asej.2015.02.005 - 45. Liu, W.C., Hsu, M.H., Kuo, A.Y. and Huang, H.Y. (2007) Effect of Channel Connection on Flow and Salinity Distribution of Danshuei River Estuary. Applied Mathematical Modelling, 31, 1015-1028.
https://doi.org/10.1016/j.apm.2006.02.005 - 46. Hsu, M.H., Kuo, A.Y., Kuo, J.T. and Liu, W.C. (1999) Procedure to Calibrate and Verify Numerical Models of Estuarine Hydrodynamics. Journal of Hydraulic Engineering, ASCE, 125, 166-182.
https://doi.org/10.1061/(ASCE)0733-9429(1999)125:2(166) - 47. Rumelhart, D.E., Hinton, G.E. and Williams, R.J. (1986) Learning Representations by Back-Propagating Errors. Nature, 323, 533-536.
https://doi.org/10.1038/323533a0 - 48. Quan, G.Z., Pan, J. and Wang, X. (2016) Prediction of the Hot Compressive Deformation Behavior for Superalloy Nimonic 80A by BP-ANN Model. Applied Sciences, 6, 66.
https://doi.org/10.3390/app6030066 - 49. Kisi, O. (2004) Multi-Layer Perceptrons with Levenberg-Marquardt Training Algorithm for Suspended Sediment Concentration Prediction and Estimation. Hydrological Sciences Journal, 49, 1025-1040.
https://doi.org/10.1623/hysj.49.6.1025.55720 - 50. Hagan, M.T. and Menhaj, M. (1994) Training Feed forward Networks with the Marquardt Algorithm. IEEE Transaction on Neural Networks, 5, 989-993.
https://doi.org/10.1109/72.329697 - 51. El-Bakyr, M.Y. (2003) Feed forward Neural Networks for K-P Interactions. Chaos, Solutions & Fractals, 18, 995-100.
https://doi.org/10.1016/S0960-0779(03)00068-7 - 52. Cigizoglu, H.K. and Kisi, O. (2005) Flow Prediction by Three Back Propagation Techniques Using k-Fold Partitioning of Neural Network Training Data. Nordic Hydrology, 36, 49-64.
- 53. Haykin, S. (1991) Neural Networks: A Comprehensive Foundation. Prentice Hall Inc., Engle Wood, 213-214.
- 54. Yang, F. and Paindavoine, M. (2003) Implementation of an RBF Neural Network on Embedded Systems: Real-Time Face Tracking and Identity Verification. IEEE Transactions on Neural Networks, 14, 1162-1175.
https://doi.org/10.1109/TNN.2003.816035 - 55. Li, M., Verma, B., Fan, X. and Tickle, K. (2008) RBF Neural Networks for Solving the Inverse Problem of Back Scattering Spectra. Neural Computing and Applications, 17, 391-397.
https://doi.org/10.1007/s00521-007-0138-2 - 56. Haykin, S. (1999) Neural Networks: A Comprehensive Foundation. 2nd Edition, Prentice Hall: Upper Saddle River.
- 57. Zirkohi, M.M., Fateh, M.M. and Akbarzade, A. (2010) Design of Radial Basis Function Network Using Adaptive Particle Swarm Optimization and Orthogonal Least Squares. Journal of Software Engineering & Applications, 3, 704-708.
https://doi.org/10.4236/jsea.2010.37080 - 58. Bjorck, A. (1967) Solving Linear Least Squares Problems by Gram-Schmidt Orthogonalization. BIT Numerical Mathematics, 7, 1-21.
https://doi.org/10.1007/BF01934122 - 59. Chen, S., Cowan, C.F.N. and Grant, P.M. (1991) Orthogonal Least Squares Learning Algorithm for Radial Basis Function Networks. IEEE Transactions on Neural Networks, 2, 302-309.
https://doi.org/10.1109/72.80341 - 60. Ham, F.M. and Kostanic, I. (2001) Principles of Neurocomputing for Science & Engineering. McGraw-Hill, New York.
- 61. Casulli, V. and Walters, R.A. (2000) An Unstructured Grid, Three-Dimensional Model Based on the Shallow Water Equations. International Journal for Numerical Methods in Fluids, 32, 331-348.
https://doi.org/10.1002/(SICI)1097-0363(20000215)32:3<331::AID-FLD941>3.0.CO;2-C - 62. Casulli, V. and Cheng, R.T. (1990) Stability Analysis of Eulerian-Lagrangian Methods for the One-Dimensional Shallow-Water Equations. Applied Mathematical Modelling, 14, 122-131.
https://doi.org/10.1016/0307-904X(90)90045-7 - 63. Zhang, Y., Baptista, A.M. and Myers III, E.P. (2014) A Cross-Scale Model for 3D Baroclinic Circulation in Estuary-Plume-Shelf Systems: I. Formation and Skill Assessment. Continental Shelf Research, 24, 2187-2214.
https://doi.org/10.1016/j.csr.2004.07.021 - 64. Sun, D., Wan, Y. and Qiu, C. (2016) Thee Dimensional Model Evaluation of Physical Alterations of the Galoosahatchee River and Estuary: Impact on Salt Transport. Estuarine, Coastal and Shelf Science, 173, 16-25.
https://doi.org/10.1016/j.ecss.2016.02.018 - 65. Velamala, S.N., Thomas, J., Bari, S. and Kachave, S. (2016) The Impact of Dredging on Residence Time in the Amba Estuary, West Coast of India. Environmental Earth Sciences, 75, 108.
https://doi.org/10.1007/s12665-015-4851-3 - 66. Cheng, C.T., Ou, C.P. and Chau, K.W. (2002) Combining a Fuzzy Optimal with a Genetic Algorithm to Solve Multiobjective Rainfall-Runoff Model Calibration. Journal of Hydrology, 268, 72-86.
https://doi.org/10.1016/S0022-1694(02)00122-1 - 67. Kisi, O., Shiri, J. and Mustafa, T. (2012) Modeling Rainfall-Runoff Using Soft Computing Techniques. Computers and Geosciences, 51, 108-117.
https://doi.org/10.1016/j.cageo.2012.07.001 - 68. Lin, J.Y., Cheng, C.T. and Chau, K.W. (2006) Using Support Vector Machines for Long-Term Discharge Prediction. Hydrologic Sciences Journal, 51, 599-612.
https://doi.org/10.1623/hysj.51.4.599 - 69. Muttil, N. and Chau, K.W. (2007) Machine-Learning Paradigms for Selecting Ecologically Significant Input Variables. Engineering Applications of Artificial Intelligence, 20, 735-744.
https://doi.org/10.1016/j.engappai.2006.11.016 - 70. Gholami, V., Chau, K.W., Fadaee, F., Torkaman, J. and Ghaffari, A. (2015) Modeling of Groundwater Level Fluctuations Using Dendrochronology in Alluvial Aquifers. Journal of Hydrology, 529, 1060-1069.
https://doi.org/10.1016/j.jhydrol.2015.09.028 - 71. Chen, X.Y., Chau, K.W. and Busari, A.O. (2015) A Comparative Study of Population-Based Optimization Algorithms for Downstream River Flow Forecasting by a Hybrid Neural Network Model. Engineering Applications of Artificial Intelligence, 46, 258-268.
https://doi.org/10.1016/j.engappai.2015.09.010 - 72. Taormina, R. and Chau, K.W. (2015) Data-Driven Input Variable Selection for Rainfall-Runoff Modeling Using Binary-Coded Particle Swarm and Extreme Learning Machines. Journal of Hydrology, 529, 1617-1632.
https://doi.org/10.1016/j.jhydrol.2015.08.022




























