American Journal of Climate Change
Vol.04 No.01(2015), Article ID:54893,20 pages
10.4236/ajcc.2015.41009
NARCCAP Model Skill and Bias for the Southeast United States
Erik D. Kabela, Gregory J. Carbone
Department of Geography, University of South Carolina, Columbia, South Carolina, USA
Email: ekabela@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 March 2015; accepted 19 March 2015; published 23 March 2015
ABSTRACT
This paper investigates dynamically downscaled regional climate model (RCM) output from the North American Regional Climate Change Assessment Program (NARCCAP) for two sub-regions of the Southeast United States. A suite of four statistical measures were used to assess model skill and biases were presented in hindcasting daily minimum and maximum temperature and mean precipitation during a historical reference period, 1970-1999. Most models demonstrated high skill for temperature during the historical period. Two outliers included two RCMs run using the Geophysical Fluids Dynamics Lab (GFDL) model as their lateral boundary conditions; these models suffered from a cold maximum temperature bias. Improvement with GFDL-based projections of maximum temperature was noted from May through November when they ran with observed sea- surface conditions (GFDL-timeslice), particularly for the east sub-region. Precipitation skill prov- ed mixed-relatively high when measured using a probability density function overlap measurement or the index of agreement, but relatively low when measured with root-mean square error or mean absolute error, because several models overestimated the frequency of extreme precipitation events.
Keywords:
NARCCAP, Model Skill, Model Bias

1. Introduction
Most global climate models (GCMs) have spatial resolution of 100 kilometers or lower?relatively coarse with respect to surface-based atmospheric processes. To address this issue, regional climate models (RCMs) are used to dynamically downscale coarse resolution GCM output. But how skillful are regional climate models? This paper uses several members of the North American Regional Climate Change Assessment Program (NARCCAP) ensemble [1] to evaluate temperature and precipitation output in the Southeast United States and to investigate potential sources of model bias. Such evaluation is relevant for water resource managers [2] , agricultural engineers and farmers [3] [4] , and forest managers [5] estimating impacts of potential temperature or precipitation changes, and for those assessing adaptive capacity to climate change [6] - [9] . Central to assessing impacts or developing adaptation policies is the spatial resolution at which climate change scenarios and the limits to predictability of some climate variables at a regional or local scale are presented [10] . Assessing model skill, performing model validation, and determining model bias will influence stakeholder confidence in future projections [11] .
Biases in RCM output occur for various reasons, but the largest source of uncertainty is derived from the GCM providing lateral boundary conditions (LBCs) [12] [13] . Differences in the physical handling of complex atmospheric processes account for the second largest source of uncertainty in RCM output [14] NARCCAP data are structured in a way that allows analysis of both of these sources of error. Each RCM was run first with “observed” boundary conditions from reanalysis data, then each was driven by a set of GCM boundary conditions. This paper uses this structure to evaluate model performance and investigate potential causes of model bias found in each regional climate model.
Although prior skill assessments of NARCCAP model output have focused on the Southeast U.S., such studies have used only a small number of NARCCAP ensemble members, and have evaluated output on only a monthly timescale [15] . This paper presents individual skill metrics for nine NARCCAP members and notes the perceived source of the NARCCAP model bias. Additionally, this work uses four metrics to assess model skill; each providing unique insights into model performance, while other studies used only one skill metric [5] [15] [16] .
Section 2 provides details on each of the datasets used for the model assessment and information on each skill metric. Section 3 provides results of individual NARCCAP ensemble member skill and attributes degradation in skill to biases found in each RCM and GCM used as part of NARCCAP.
2. Data and Methods
The study area for this analysis focuses on the Southeast United States, defined here as Alabama, Mississippi, Tennessee, Georgia, and North and South Carolina (Figure 1). Further, the study area is broken into two sub- regions: a west sub-region made up of Alabama, Mississippi, and Tennessee; and an east sub-region made up of Georgia, and North and South Carolina. Breaking the Southeast U.S. into two sub-regions was done due to the micro-, meso-, and synoptic-scale patterns that impact the two sub-regions differently due to the influence of the Appalachian Mountains and the Atlantic and Gulf Coasts. Similar, yet slightly different, east-west sub-division is noted in work conducted by Bukovsky (2011) [17] , and similar sized sub-domain-based analysis has been conducted for other regional climate model assessments [18] .
Figure 1. Southeast U.S. study area with the east sub-region (dark gray) and west sub-region (light gray) highlighted.
2.1. Data
2.1.1. NARCCAP Ensemble Models
Modeling runs for NARCCAP were conducted for the “present climate” (1979-2004) with NCEP/DOE Reanalysis II data [19] as boundary conditions as Phase I of NARCCAP and another run in the reference climate (1968-2000) using four GCMs as LBCs comprised Phase II [1] . The NCEP/DOE Reanalysis II dataset provides the equivalent of observed data as boundary conditions for RCMs and allows for the assessment of uncertainties and bias from the RCMs alone. NARCCAP runs were also conducted for future climate (2038-2070) using the Special Report on Emissions Scenarios (SRES) [20] A2 emission scenario.
For this work, nine NARCCAP ensemble members were utilized. Members were chosen based on a necessity to compare a myriad of RCM-GCM combinations, while focusing on multiple runs of the same RCM with differing LBCs. Table 1 provides information on the NARCCAP ensemble members used in this research. In addition to the eight models listed in Table 1, data from the Geophysical Fluid Dynamics Laboratory (GFDL) model timeslice experiment provided a third RCM run with the GFDL GCM. In the timeslice experiments, the atmospheric component of the GCM is run without the full-coupled ocean component of the model. Instead, the boundary conditions for sea surface and ice for the reference period are based on observed data, and boundary conditions for the future period are derived by perturbing the same observed sea-surface temperature and ice data by an amount based on the results of a lower-resolution run of the full GCM. Excluding the coupled ocean model allows the atmospheric model to be run at much higher resolution because the computational requirements are much lower.
2.1.2. Global Climate Models
The GCMs used as boundary conditions were generated for the International Panel on Climate Change’s (IPCC) Fourth Assessment [21] by the World Climate Research Program’s (WCRP’s) Working Group on Coupled Modeling (WGCM) and hosted on a server at Lawrence Livermore National Laboratory’s (LLNL) Program for Climate Model Diagnosis and Intercomparison (PCMDI). To provide a consistent, meaningful, and robust analysis, it was important for multiple models to share the same LBCs. Specifically, GCMs used in this work include the Community Climate System Model (CCSM) [22] , the Third Generation Coupled Global Climate Model (CGCM3) [23] , and the GFDL GCM [24] .
2.1.3. Observed Dataset
A gridded meteorological dataset developed by the University of Washington (hereafter, Maurer dataset) serves as the observed dataset. It is described in Maurer et al. (2002) [25] and available for download at
http://www.engr.scu.edu/~emaurer/data.shtml. The Maurer dataset has daily temporal resolution of minimum and maximum air temperature and precipitation from 1950 to 1999 and a spatial resolution of 12 kilometers, covering a domain from 25.125˚N to 52.875˚N latitude and −124.625˚E to −67.000˚E longitude. Additionally, the Maurer dataset treats interactions at the land-atmosphere interchange in a way that is physically superior to
Table 1. Acronyms, full names with references, and modeling groups of RCMs involved in NARCCAP and this paper.
reanalysis data. Unlike reanalysis data, the Maurer dataset does not employ the use of soil moisture “nudging” or adjusting, which results in failed closure of the surface water budget. Maurer et al. (2001) [26] showed that the nonclosure term can be of the same order as other terms (e.g., runoff) in the surface water cycle. Although nudging in reanalysis data is designed to bring the model (especially atmospheric moisture variables) closer to observations, this is done at the expense of other components of the water budget, and complicates studies focused on the interaction and variability of water budget components at the land surface (like temperature and precipitation). Maurer et al. (2000, 2001) [26] [27] argue that physically-based land surface model forced with quality controlled surface variables produce better data for diagnosis of land surface water budget simulations.
2.2. Data Extraction
To maintain methodological consistency with Perkins’ skill score calculation described in the next subsection and adapted from Perkins et al. (2007) [28] , daily values of minimum and maximum temperature and mean precipitation from the dynamically downscaled results and observed data were extracted for the period 1970-1999 from grid points located inside and within a half-degree of the boundaries of the two Southeast sub-regions (east and west). Kjellstrom et al. (2010) [18] found the same skill score metric based on daily data excluding dry events, or monthly data including both wet and dry events, gave very different results in terms of model ranking relative to precipitation output. This was most likely a result of a difference in the underlying probability density functions (PDFs). The same daily data values extracted for the Perkins method were also used for calculation of Willmott’s index of agreement, RMSE, and MAE. For comparison of the NARCCAP ensemble members to the NARR and NCEP-driven RCM hindcasts, daily data from 1979-1999 were extracted from the same grid points. A half-degree buffer was chosen due to the spatial resolution of the data and that the data points may not completely lie on or within state boundaries, yet are representative of some portion of the region and sub-region. By extracting daily values at each grid point, it is possible to gauge a model’s ability to simulate day-to-day variability rather than long-term averages, giving a proper gauge for testing a model’s worth.
Although individual grid points were extracted within the six states classified as the Southeast U.S., all analysis was conducted by aggregating data to the sub-regional scale (rather than grid point by grid point) for several reasons. First, the PDF skill score metric was designed by Perkins et al. (2007) [28] for determination of GCM skill across all of Australia (for the entire country rather than at individual grid locations) and is used in the same manner for regional climate model skill assessments [15] [29] . To maintain methodological consistency with others studies using Perkin’s method, aggregation was necessary. Additionally, although Kjellstrom et al. (2010) [15] display skill scores spatially throughout Europe, they average individual grid skill scores to obtain a single skill score for each of their defined sub-regions. Second, aggregating data into sub-regions allows for meso- and synoptic-scale pattern recognition which may not be evident when analyzing at each grid location. To further this point, GCMs were not meant to represent conditions at a single grid point but are more representative of the synoptic-scale (100 s to 1000 s of kilometers). Although RCMs are still not representative of a single grid location they are representative of the meso-scale (10 s to 100 s of kilometers). Third, most crop and hydrological assessments aggregate information from the single grid point scale to a field (or multi-field) or watershed-scale [30] [31] and assessing skill and bias on a sub-regional level is adequate. Lastly, although the information contained within an individual RCM grid better represents conditions within the grid point, models run at 50 km resolution will still have issues with pinpointing information at a specific location (e.g., town, city, weather station, etc.).
2.3. Methods
Characterization of climate model forecast skill begins with determining how closely a model’s output matches observations. Model skill was measured against the Maurer gridded observed dataset [25] for the Southeast U.S. for monthly minimum and maximum temperature and mean precipitation (utilizing daily data) during a historical reference period, 1970-1999. Skill was determined through calculation of four metrics: probability density function overlap [28] , an index of agreement [32] , root mean square error, and mean absolute error.
2.3.1. PDF (Perkins) Skill Score
We generated probability density functions (PDFs) for monthly minimum and maximum temperature and mean precipitation from each of the downscaling approaches as well as gridded observations for the Southeast U.S. PDFs can be a convenient way of condensing a vast amount of data to find probability of occurrence of an event [33] - [35] . We calculated the cumulative minimum value of two distributions of a binned value (defined by the user), measuring the common area between two PDFs [28] :
 (1)
(1)
where n is the number of bins used to calculate the PDF, Zm is the frequency of values in a given bin from the model, and Zo is the frequency of values in a given bin from the observed data. Temperature minimum and maximum bins were chosen as the minimum and maximum found in each month’s observations, respectively, with a bin size of 0.5˚C, while precipitation ranged from 1 mm∙day−1 to the maximum monthly value from observations, respectively, with a bin size of 1 mm∙day−1. Smaller bin sizes allow for the determination of skill with increased precision while larger bin sizes not only reduce precision but lead to slightly higher skill scores due to smoothing of the PDF. Precipitation values below 1 mm∙day−1 were not included in the analysis as part of the dataset to create the PDFs because it contributes little to daily precipitation [36] [37] .
This method of determining model skill is highly robust because its calculation does not rely on the underlying data distribution. Perkins’ skill scores are based on a scale from zero to one. If the model is able to simulate the reference climate (represented by observed gridded data) adequately, model Perkins’ skill score will be high. Conversely, if the model is unable to simulate the day-to-day variability found in the reference climate adequately, model Perkins’ skill score will be low. Perkins’ method has been used to determine model skill with coarse GCM data [28] [38] - [41] and more recently with RCM output from ENSEMBLES [18] [29] . The method has yet to be applied to individual RCM output from NARCCAP. This simple method gives decision makers insight into model skill in the historical reference period and how much confidence they can place in its projections for future climate, as well as provide information on individual model bias.
2.3.2. Index of Agreement
Willmott et al. (2012) [32] provide another method used to validate model performance. Their dimensionless index of agreement (dr) is computed by finding the magnitudes of the differences between the model-predicted and observed deviations about the observed mean relative to the sum of the magnitudes of the perfect model and observed deviations about the observed mean [32] . The modified index of agreement is based on the original form of Willmott’s index of agreement [42] [43] . Equation (2) illustrates the revised index of agreement presented in Willmott et al. (2012) [32] , of which dr is based:
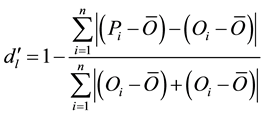 (2)
(2)
where n is the number of values, Pi are the predicted values (model), Oi are the observed values, 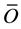 is the observed mean. Equation (2) is unbounded at the lower values, thus Willmott et al. (2012) [32] chose to refine the index of agreement such that the metric was bounded between −1 and 1. The refined index of agreement is reduced from Equation (2) and written in the form illustrated in Equation (3):
is the observed mean. Equation (2) is unbounded at the lower values, thus Willmott et al. (2012) [32] chose to refine the index of agreement such that the metric was bounded between −1 and 1. The refined index of agreement is reduced from Equation (2) and written in the form illustrated in Equation (3):
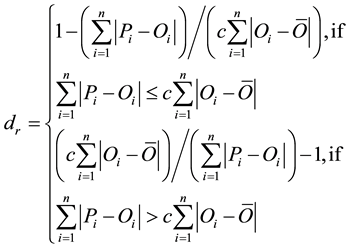 (3)
(3)
where c = 2, representing the two mean absolute deviation terms in the numerator of Equation (2). Values close to 1 indicate strong agreement between model and observations while index number approaching −1 illustrate strong deviation of the modeled result from observations. Willmott et al. (2012) [32] argue their modified index is an improvement over other non-dimensional techniques described in several published articles [44] - [47] because of its flexibility, its well-behaved nature, and because it can be used in a multitude of model-performance applications.
2.3.3. Root Mean Square Error and Mean Absolute Error
Equation (4) illustrates the computation of RMSE:
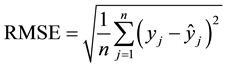 (4)
(4)
where n is the number of values, yj are the observed values, and  are the modeled values. Equation (5) illustrates the computation of MAE, following the same notation as RMSE:
are the modeled values. Equation (5) illustrates the computation of MAE, following the same notation as RMSE:
 (5)
(5)
Direct comparison of specific daily values from GCM-driven RCM runs were not compared to specific observational values (i.e., January 1, 1979 in the GCM-driven runs were not compared to January 1, 1979 in the observational record) to compute RMSE and MAE because although GCM-based runs have a date and time associated with the output, the output is simply a general time keeping measure. However, over the course of a lengthy climatology (20 - 30 years) the intra- and inter-annual variability shown in observations is also illustrated in the GCM-based climatology. For this reason, daily data values for each month within both sub-regions were sorted from lowest to highest with the assumption that general values found in the GCM-driven RCMs are found at some instance in the observational record of the same period.
RMSE is commonly reported in the climatological/meteorological peer-reviewed literature to express model error and aid in quantifying model skill compared to observations [48] - [53] . Additionally, RMSE is a preferred method of expressing model accuracy because it not only includes contributions from each individual data point, but also includes any mean bias error [52] [54] [55] . However, Willmott and Matsuura (2005) [56] argue mean absolute error (MAE) should be reported because it represents a more natural measure of average error with a clearly defined meaning, something RMSE lacks. Both values indicate dimensional (i.e., ˚C for temperature and either percent or mm∙day−1 for precipitation) mean model error compared to observations; however, large errors have a relatively greater influence on RMSE than MAE. Both methods were chosen to represent mean model error/skill because a suite of measures is appropriate to gain a well-rounded assessment of skill (Willmott, 1981).
2.4. Model Bias
Another important aspect of this research was to determine why a model may lack skill. A first step towards this is to determine whether bias occurs in a particular part of a variable’s frequency distribution. To this end, Kjellstrom et al. (2010) [18] computed area-average model bias at the 1st, 5th, 10th, 25th, 50th, 75th, 90th, 95th, and 99th percentiles for each of their sub-regions, variables, and models. This method allows for determination of where, within the probability density function (or distribution), a model under or over predicts a given variable, leading to degradation in skill. For example, a model with a warm temperature bias in the lower percentiles (the coldest days) may decrease the number of cold air outbreaks and potential decrease snow cover in the region during winter. A model with a warm summer bias in the upper percentiles could cause over prediction of heat waves and drought. In this study, model bias at each percentile was computed for each combination of RCM-NCEP output from NARCCAP Phase I, RCM-GCM results from NARCCAP Phase II, and the three GCMs from the 4th IPCC assessment.
3. Results
Results of model skill and bias are presented in the following subsections for minimum and maximum temperature and mean precipitation. Findings are reported for the entire Southeast, however, the percentile plots displayed and referenced in the paper are taken from one month for each season to provide tangible examples for the east sub-region.
3.1. Minimum Temperature
Each member of the NARCCAP ensemble replicates observed minimum temperature well. Perkins skill scores for most RCMs (with the exception of the WRFG models, and RCM3-GFDL and ECP2-GFDL) remain above 0.7 for each month. Index of agreement values generally exceeds 0.5 in each month in both eastern (Figure 2(a) and Figure 2(b)) and western portions (Figure 3(a) and Figure 3(b)) of the study region. RMSE and MAE values typically remain below 3˚C for most models (Figure 2(c) and Figure 2(d); Figure 3(c) and Figure 3(d)). For the WRFG RCMs, ECP2-GFDL, and GFDL-timeslice, July and August show the worst skill. The degradation in skill for the WRFG RCMs and ECP2-GFDL are attributed to a cold bias between 1˚C to 3˚C as illustrated for July in Figure 4(c). Additionally, the WRFG model illustrates a slight cold bias in the same months for the NCEP-driven runs (e.g., Figure 5(c)). The ECP2-GFDL’s cold bias in July and August must be a function of the GFDL LBCs, as the NCEP-driven runs of the ECP2 model illustrate a warm bias in all months between 1˚C and 4˚C (Figure 5(c)). The GFDL-timeslice, on the other hand, exhibits a warm bias of 2˚C to 5˚C from the 50th through 99th percentiles. The cold bias presented in the GFDL GCM over the Southeast U.S. is noted in Freidenreich and Ramaswamy (2011) [57] by a deficit in modeled downward shortwave radiationflux compared to observations. Further, the authors conclude the deficit in downwelling shortwave radiation is due to an over prediction of total cloud amount when compared to observations. The best performing models are the RCM3- CGCM3 and CRCM-CGCM3 which show very little warm or cold bias, remaining within ±2˚C of observations across all percentiles and months, and only a 1˚C to 2˚C warm bias in the NCEP-driven runs. Although a bias of 1˚C to 2˚C may seem rather large, it falls within a commonly known and accepted threshold in climate models [58] [59] .
Interestingly, the two models driven by GFDL exhibit degradation in skill in the winter and early spring, an observation not found in the other ensemble members. Percentile plots reveal these RCMs suffer from significant cold bias between 4˚C and 8˚C. This strong cold bias is passed from the GFDL model to each RCM (Figure 6). Conversely, the CCSM GCM exhibits a warm bias between 1˚C and 5˚C in most months which is tempered
Figure 2. Perkins’ skill score (a), Willmott’s index of agreement (b), mean absolute error (c), and root mean square error (d) for east sub-region minimum temperature.
Figure 3. Perkins’ skill score (a), Willmott’s index of agreement (b), mean absolute error (c), and root mean square error (d) for west sub-region minimum temperature.
Figure 4. Percentile plots of minimum temperature bias for the east sub-region from nine NARCCAP ensemble members for January (a), April (b), July (c), and October (d). Labels for the NARCCAP ensemble members: “1” = MM5I-CCSM”, “2” = RCM3-GFDL, “3” = ECP2-GFDL, “4” = WRFG-CCSM, “5” = WRFG-CGCM3, “6” = RCM3-CGCM3, “7” = CRCM- CGCM3, “8” = CRCM-CCSM, and “9” = GFDL-timeslice.
Figure 5. Percentile plots of minimum temperature bias for the east sub-region from each NARCCAP RCM run with NCEP reanalysis LBCs for January (a), April (b), July (c), and October (d). Labels for the NARCCAP ensemble members: “1” = CRCM, “2” = ECP2, “3” = MM5I, “4” = RCM3, and “5” = WRFG.
slightly in the downscaling process by both the MM5I and CRCM, resulting in a slight warm bias of not more than 2˚C in any given month.
Percentile plots for the west sub-region reveal the RCM3-GFDL and ECP2-GFDL models have a more pronounced cold bias than the eastern sub-region, with cold biases from December through March on the order of 4˚C to 10.5˚C for the lower 50th percentiles. The cold bias must be a function of the GFDL LBCs as both the ECP2 and RCM3 RCMs have a warm bias of 1˚C to 3˚C from December through March with the NCEP-driven runs. Conversely, the GFDL-timeslice’s warm bias observed in the east sub-region (2˚C to 5˚C warm bias in above-median temperatures) is even greater in the west sub-region (3˚C to 8˚C warm bias in above-median temperatures), the result of a strong warm bias in the same percentiles with the driving GCM. This bias during the warmest months of the year, especially in the upper percentiles, may have the potential to lead to an increase in nocturnal evaporation from the soil [60] . Enhanced nocturnal evaporation aids rapid daytime temperature increases and contribute to an increased number of heat waves, leading to a positive feedback wherein evaporation is increased leading to drier soil (assuming little to no replenishment) which perpetuates the warm cycle [61] .
3.2. Maximum Temperature
Maximum temperature is less skillfully predicted, showing higher bias in both sub-regions. The RCM3-GFDL and ECP2-GFDL models, in particular, show strong cold bias, especially as measured by RMSE and MAE (Figures 7-9). The low skill values are attributed to a cold bias in the GFDL GCM (Figure 10) from winter through mid spring between 3˚C and 7˚C. Although two models with the same LBCs show relatively little skill
Figure 6. Percentile plots of minimum temperature bias for the east sub-region from the GCMs used as boundary conditions in NARCCAP for January (a), April (b), July (c), and October (d). Labels for the NARCCAP ensemble members: “1” = CCSM, “2” = GFDL, and “3” = CGCM3.
Figure 7. Perkins’ skill score (a), Willmott’s index of agreement (b), mean absolute error (c), and root mean square error (d) for east sub-region maximum temperature.
Figure 8. Perkins’ skill score (a), Willmott’s index of agreement (b), mean absolute error (c), and root mean square error (d) for west sub-region maximum temperature.
Figure 9. Percentile plots of maximum temperature bias for the east sub-region from nine NARCCAP ensemble members for January (a), April (b), July (c), and October (d). Labels for the NARCCAP ensemble members: “1” = MM5I-CCSM”, “2” = RCM3-GFDL, “3” = ECP2-GFDL, “4” = WRFG-CCSM, “5” = WRFG-CGCM3, “6” = RCM3-CGCM3, “7” = CRCM-CGCM3, “8” = CRCM-CCSM, and “9” = GFDL-timeslice.
Figure 10. Percentile plots of maximum temperature bias for the east sub-region from the GCMs used as boundary conditions in NARCCAP for January (a), April (b), July (c), and October (d). Labels for the NARCCAP ensemble members: “1” = CCSM, “2” = GFDL, and “3” = CGCM3.
in replicating daily maximum temperature and have high RMSE and MAE values, the fact the RCM3-CGCM3 illustrates relatively little skill points to a systematic error within the RCM3 itself (Figure 11), and is not simply an issue of the GCM providing biased LBCs. Conversely, the CRCM-CCSM suffers a reduction in skill from July through September, a direct result of the model exhibiting a strong warm bias from the 50th percentile to the 99th percentile and a lesser warm bias in the 1st through 50th percentiles. Part of the warm bias can be attributed to the CCSM GCM which shows a warm bias from the 50th through the 99th percentiles and a slight warm bias of less than 2˚C from the 1st through 50th percentiles while the other part is attributed to the strong warm bias observed with the NCEP-driven runs of the CRCM observed over the same period.
Percentile plots (Figure 10) highlight the significant cold bias found within the GFDL-based NARCCAP ensemble members, leading to low skill scores and high RMSE and MAE values. Most months exhibit a cold bias on the order of 4˚C with values as low as 9˚C and 10˚C in winter. Four of the nine NARCCAP members have a cold bias greater than 4˚C during the months encompassing boreal winter, spring, and mid to late fall. The cold bias observed with the GCM-driven runs is partially attributed to the persistent cold bias observed in most months (and percentiles) for each RCM driven with NCEP LBCs. Percentile plots also reveal the CRCM-CCSM suffers from a warm bias, most pronounced from June through September with the largest warm bias occurring from the 50th to 99th percentiles.
An interesting comparison between the GFDL-driven (RCM-based runs) and the GFDL-timeslice reveals the GFDL-timeslice typically outperforms the RCM-driven GFDL runs, with higher skill-based values and lower error/bias values. This demonstrates how the use of observed sea-surface conditions in the timeslice experiment results in more accurate projections than using GCM-based sea-surface conditions. Additionally, it should be
Figure 11. Percentile plots of maximum temperature bias for the east sub-region from each NARCCAP RCM run with NCEP reanalysis LBCs for January (a), April (b), July (c), and October (d). Labels for the NARCCAP ensemble members: “1” = CRCM, “2” = ECP2, “3” = MM5I, “4” = RCM3, and “5” = WRFG.
noted that the separation of skill and bias metrics of the GFDL-driven models are not significantly different with respect to minimum temperature but are (in some instances) with respect to maximum temperature. This may suggest that the inclusion of observed sea-surface conditions in a regional climate model impacts maximum temperatures more than minimum temperatures. Solman et al. (2008) [62] noted in their RCM-timeslice experiment that maximum temperatures are better represented than minimum temperatures when compared to observations.
The most consistent and least bias model in both sub-regions is the MM5I-CCSM with Perkins skill scores and Willmott values exceeding 0.75, and low RMSE and MAE values between 0.5˚C and 2˚C. Percentile plots concur with the MM5I-CCSM’s skillfulness by showing the model rarely deviates beyond ±2˚C from observations across all percentiles (Figure 9). The only months in which the MM5I-CCSM observes a small deviation in skill are December, August, and November when the model exhibits a consistent bias throughout all percentiles (slight cold bias in December and November; slight warm bias in August). The MM5I-CCSM is the only model (with respect to temperature) to attain Perkins skill scores of greater than 0.9 for at least eight months, Willmott values of 0.85 for at least eight months, and RMSE and MAE values less than 1.5˚C for 10 months.
3.3. Mean Precipitation
Skill associated with NARCCAP output of mean precipitation in the Southeast varies by metric. No discernible relationship between Perkins/Willmott scores and RMSE/MAE for precipitation was found, indicating these metrics quantitatively measure non-Gaussian distributions much differently, with outliers having a much larger impact in the calculation of RMSE and MAE than in Perkins or Willmott’s methods. Very rarely is a models’ Perkins or Willmott skill score below 0.8, indicating the models are able to adequately reproduce the daily data distribution found in observations, especially considering most data points are contained within the left tail of the distribution, with a very small number comprising the right tail of the distribution. However, a high RMSE and MAE, coupled with high Perkins skill score, indicates the model either under- or over-predicts the quantity and/or frequency of precipitation events in the upper percentiles (from 75th through 99th percentile). Although the upper percentiles account for an extremely small portion of the data distribution (while still having a large impact on daily total rainfall), their impact on RMSE and MAE is significant because these values are large outliers from the mean. With few exceptions, Perkins skill scores for most models exceed 0.8, with several in the 0.85 to 0.95 range for both sub-regions (Figure 12 and Figure 13). Additionally, Willmott index of agreement values mostly fall within the 0.82 to 0.96 range.
The only models to exhibit degradation in Perkins and Willmott skill scores in the east sub-region are the CRCM-CGCM3 and CRCM-CCSM in September and October, with Perkins skill scores between 0.7 and 0.8 (save for CRCM-CGCM3’s September Perkins skill score between 0.8 and 0.85) and Willmott values between 0.75 and 0.85. Percentile plots (Figure 14) reveal the CRCM RCMs exhibit a dry bias across all percentiles, but is most pronounced from the 50th through 99th percentiles and ranges between 30% and 60% below observations. A similar dry bias is observed from the winter through mid spring and fall for the NCEP-driven runs of the CRCM (Figure 15). In terms of real numbers, assume the 75th percentile value from observations was 100 mm∙day−1, a 30% to 60% dry bias would mean the model predicts the 75th percentile value to fall between 40 and 70 mm∙day−1. RMSE and MAE values are high because of the magnitude of model bias, and because of the range of values across which model exhibit bias.
The west sub-region performs slightly worse than the east sub-region with regards to Perkins and Willmott scores, moreover, RMSE and MAE values are higher for most models, particularly in the winter and spring months. Percentile plots reveal, from December through May, almost all models have a dry bias in the lower 50th percentiles between 5% and 30%. Although Perkins and Willmott scores are respectable during this period (between 0.8 and 0.9 for both, respectively), indicating the models are able to replicate the daily precipitation pattern, they fail to generate lighter precipitation found in the bottom half of the distribution.
Figure 12. Perkins’ skill score (a), Willmott’s index of agreement (b), mean absolute error (c), and root mean square error (d) for east sub-region mean precipitation.
Figure 13. Perkins’ skill score (a), Willmott’s index of agreement (b), mean absolute error (c), and root mean square error (d) for west sub-region mean precipitation.
Figure 14. Percentile plots of mean precipitation bias for the east sub-region from nine NARCCAP ensemble members for January (a), April (b), July (c), and October (d). Labels for the NARCCAP ensemble members: “1” = MM5I-CCSM”, “2” = RCM3-GFDL, “3” = ECP2-GFDL, “4” = WRFG-CCSM, “5” = WRFG-CGCM3, “6” = RCM3-CGCM3, “7” = CRCM-CGCM3, “8” = CRCM-CCSM, and “9” = GFDL-timeslice.
Figure 15. Percentile plots of mean precipitation bias for the east sub-region from the GCMs used as boundary conditions in NARCCAP for January (a), April (b), July (c), and October (d). Labels for the NARCCAP ensemble members: “1” = CCSM, “2” = GFDL, and “3” = CGCM3.
GCM-based percentile plots (Figure 15) illustrate all three models stay within a bias of ±15% below the 50th percentile, steadily increasing to a dry bias between 20% and 65% at the 99th percentile. Most RCMs, except those run by the CCSM GCM, show less dry bias at the higher percentiles. However, some models overcompensate and what was once a dry bias within the GCM becomes a wet bias of the same magnitude in the RCM. This finding is attributed to the wet bias observed consistently in the ECP2, MM5I, and WRFG NCEP-driven models (Figure 16) for all months. Additionally, the RCM3-NCEP model illustrates a pronounced wet bias in the highest percentiles from spring through mid summer.
More than half of the models have a wet bias in the 50th through 99th percentiles and is a function of a wet bias in the same percentiles for each RCM driven by NCEP boundary conditions. These precipitation amounts do not adequately replenish water supplies and sub-surface moisture due to high runoff rates. Even more troubling is the dry bias observed from most models during the summer across all percentiles. The dry bias within the GCMs noted for the east sub-region is slightly greater in the west sub-region which is maintained, and in some cases enhanced, within the RCMs. The dry bias must be attributed to the GCMs because each RCM run with NCEP LBCs illustrates a wet bias during the summer, with the exception of the WRFG from the 5th through 50th percentiles and the CRCM from the 90th to 99th percentiles. Although observations show extreme precipitation (both high and low) is increasing across the Northern Hemisphere [63] and U.S. [64] , the models exhibit a propensity toward high-end exaggeration.
4. Conclusions
This paper uses four statistically-based measures to assess daily temperature and precipitation output (by month) from nine NARCCAP ensemble members in the Southeast United States for an historical reference period,
Figure 16. Percentile plots of mean precipitation bias for the east sub-region from each NARCCAP RCM run with NCEP reanalysis LBCs for January (a), April (b), July (c), and October (d). Labels for the NARCCAP ensemble members: “1” = CRCM, “2” = ECP2, “3” = MM5I, “4” = RCM3, and “5” = WRFG.
1970-1999. Most models demonstrated high skill for maximum and minimum temperature. The outlier models included two RCMs run with the Geophysical Fluids Dynamics Lab (GFDL) as their lateral boundary conditions; these models exhibited a cold maximum temperature bias, attributed to erroneously high soil moisture. Precipitation output showed mixed skill?relatively high when measured using a probability density function overlap measure or the index of agreement, but relatively low when measured with root-mean square error or mean absolute error, because the majority of models overestimate the frequency of extreme precipitation events.
All models reproduce daily minimum temperature trends relatively skillfully. The WRFG RCMs (run with CCSM and CGCM3 LBCs), the ECP2-GFDL, and GFDL-timeslice show reduced skill during the summer months (June, July, and August) while the RCM3-GFDL and ECP2-GFDL exhibit slight degradation from December through March. The most consistently skillful models across all months are the RCM3- and CRCM- CGCM3. Additionally, the WRFG RCMs and ECP2-GFDL exhibit a minimum temperature cold bias of 2˚C - 4˚C across all percentiles during the summer while the GFDL-timeslice exhibits a warm bias between 2˚C and 4˚C below the 50th percentile and 4˚C to 8˚C above the 50th percentile. December through March cold bias between 4˚C and 10˚C plagues the RCM3- and ECP2-GFDL models. Less overall skill is observed for all models with respect to maximum temperature. The worst performing models are the RCM3- and ECP2-GFDL with strong cold biases between 2˚C and 10˚C for several months. Degradation in skill is caused by a cold bias exhibited in the GFDL GCM that is transmitted and enhanced thought the downscaling process. The most skillful model across all months is the MM5I-CCSM in both sub-regions.
Performance of monthly mean precipitation varies by skill metric. With the Perkins’ and Willmott’s methodologies, the MM5I-CCSM is the most consistently skillful in all months, and the WRFG RCMs and CRCM- CCSM are the least skillful. By contrast, using RMSE suggests the CRCM RCMs are the most consistently skillful while the WRFG-CGCM3 and GFDL-timeslice are the least skillful. These differences demonstrate that complexity of assessing precipitation skill and the need to incorporate several skill metrics. Additionally, the WRFG RCMs overestimate either the frequency or magnitude of daily mean precipitation as they consistently exhibit wet bias of 15% to 30% (sometimes higher) above the 50th percentile. The CRCM RCMs illustrate a consistent dry bias between 10% and 40% for most percentiles and months, indicating they underestimate either the frequency or magnitude of daily mean precipitation.
Finally, Perkins’ skill score, Willmott’s index of agreement, RMSE, and MAE are strongly correlated relative to minimum and maximum temperature because the temperature values are constrained within the Gaussian distribution such that large outliers are rarely observed (as 99.5% of the data values are contained within three standard deviations of the mean). However, little correlation is found between RMSE/MAE and either Willmott’s or Perkins’ methods relative to mean precipitation. Large outliers from the mean are inherent in the gamma distribution (precipitation) and are enhanced in the calculation of RMSE and MAE because of its value-by-value comparison but not the other two metrics, which evaluate on value-by-value basis relative to the underlying data distribution. This finding indicates multiple statistical metrics should be used to assess rather than one, which is the common approach to model validation in climate research.
References
- Mearns, L.O., Gutowski, W., Jones, R., Leung, R., McGuinnis, S., Nunes, A. and Qian, Y. (2009) A Regional Climate Change Assessment Program for North America. EOS Transactions of the American Geophysical Union, 90, 311-312. http://dx.doi.org/10.1029/2009EO360002
- Vorosmarty, C.J., Green, P., Salisbury, J. and Lammers, R.B. (2000) Global Water Resources: Vulnerability from Climate Change and Population Growth. Science, 289, 284-288. http://dx.doi.org/10.1126/science.289.5477.284
- Tubiello, F.N., Soussana, J.-F. and Howden, S.M. (2007) Crop and Pasture Response to Climate Change. Proceedings of the National Academy of Sciences of the United states of America, 104, 19686-19690. http://dx.doi.org/10.1073/pnas.0701728104
- Kruijt, B., Witte, J.-P.M. Witte, Jacobs, C.M.J. and Kroon, T. (2008) Effects of Rising Atmospheric CO2 on Evapotranspiration and Soil Moisture: A Practical Approach for the Netherlands. Journal of Hydrology, 349, 257-267. http://dx.doi.org/10.1016/j.jhydrol.2007.10.052
- Shem, W.O., Mote, T.L. and Shepard, J.M. (2010) Validation of NARCCAP Climate Products for Forest Resource Applications in the Southeast United States. 18th Conference on Applied Climatology, Session 10, American Meteorological Society.
- Smith, J.B., Vogel, J.M. and Cromwell III, J.E. (2009) An Architecture for Government Action on Adaptation to Climate Change. An Editorial Comment. Climatic Change, 95, 53-61. http://dx.doi.org/10.1007/s10584-009-9623-1
- Brooks, N., Adger, W.N. and Kelly, P.M. (2005) The Determinants of Vulnerability and Adaptive Capacity at the National Level and the Implications for Adaptation. Global Environmental Change, 15, 151-163. http://dx.doi.org/10.1016/j.gloenvcha.2004.12.006
- Dessai, S., Goulden, M., Hulme, M., Lorenzoni, I., Nelson, D.R., Naess, L.O., Wolfe, J. and Wreford, A. (2009) Are There Social Limits to Adaptation to Climate Change? Climatic Change, 93, 335-354. http://dx.doi.org/10.1007/s10584-008-9520-z
- Pielke, R.A., Prins, G., Rayner, S. and Sarewitz, D. (2007) Climate Change 2007: Lifting the Taboo on Adaptation. Nature, 445, 597-598. http://dx.doi.org/10.1038/445597a
- Cutter, S., Osman-Elasha, B., Campbell, J., Cheong, S.-M., McCormick, S., Pulwarty, R. and Ziervogel, G. (2012) Managing the Risks from Climate Extremes at the Local Level. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation. A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change (IPCC), Cambridge University Press, Cambridge.
- Seneviratne, S.I., Nicholls, N., Easterling, D., Goodess, C.M., Kanae S., Kossin, J., Luo, Y., Marengo, J., McInnes, K., Rahimi, M., Reichstein, M., Sorteberg, A., Vera, C. and Zhang, X. (2012) Changes in Climate Extremes and Their Impacts on the Natural Physical Environment. Managing the Risks of Extreme Events and Distasters to Advance Climate Change Adaptation. A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change (IPCC), Cambridge University Press, Cambridge.
- Deque, M., Rowell, D.P., Luthi, D., Giorgi, F., Christensen, J.H., Rockel, B., Jacob, D., Kjellstrom, E., de Castro, M. and van den Hurk, B. (2007) An Intercomparison of Regional Climate Simulations for Europe: Assessing Uncertainties in Model Projections. Climatic Change, 81, 53-70. http://dx.doi.org/10.1007/s10584-006-9228-x
- Jacob, D., Barring, L., Christensen, O.B., Christensen, J.H., de Castro, M., Deque, M., Giorgi, F., Hagemann, S., Hirschi, M., Jones, R., Kjellstrom, E., Lenderink, G., Rockel, B., Sanchez, E., Schar, C., Seneviratne, S.I., Somot, S., van Ulden, A. and van den Hurk, B. (2007) An Inter-Comparison of Regional Climate Models for Europe: Model Performance in Present-Day Climate. Climatic Change, 81, 31-52. http://dx.doi.org/10.1007/s10584-006-9213-4
- Giorgi, F. (2006) Regional Climate Modeling: Status and Perspectives. Journal de Physique IV France, 139, 101-118. http://dx.doi.org/10.1051/jp4:2006139008
- Sobolowski, S. and Pavelsky, T. (2012) Evaluation of Present and Future North American Regional Climate Change Assessment Program (NARCCAP) Regional Climate Simulations over the Southeast United States. Journal of Geophysical Research, 117, D01101.
- Schliep, E.M., Cooley, D., Sain, S.R. and Hoeting, J.A. (2010) A Comparison Study of Extreme Precipitation from Six Different Regional Climate Models Via Spatial Hierarchical Modeling. Extremes, 13, 219-239. http://dx.doi.org/10.1007/s10687-009-0098-2
- Bukovsky, M.S. (2011) Masks for the Bukovsky Regionalization of North America. Regional Integrated Sciences Collective, Institute for Mathematics Applied to Geosciences, National Center for Atmospheric Research, Boulder.
- Kjellstrom, E., Boberg, F., Castro, M., Christensen, J.H., Nikulin, G. and Sanchez, E. (2010) Daily and Monthly Temperature and Precipitation Statistics as Performance Indicators for Regional Climate Models. Climate Research, 44, 135-150. http://dx.doi.org/10.3354/cr00932
- Kanamitsu, M., Ebisuzaki, W., Woollen, J., Yang, S.-K., Hnilo, J.J., Fiorino, M., and Potter and G.L. (2002) NCEP- DOE AMIP-II Reanalysis (R-2). Bulletin of the American Meteorological Society, 83, 1631-1643. http://dx.doi.org/10.1175/BAMS-83-11-1631
- Nakicenovic, N. and Swart, R., Eds. (2000) Special Report on Emissions Scenarios. A Special Report of Working Group III of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge.
- IPCC (2007) Climate Change 2007: The Physical Basis. Cambridge University Press, Cambridge.
- Collins, W.D., et al. (2006) The Community Climate System Model: CCSM3. Journal of Climate, 19, 2122-2143. http://dx.doi.org/10.1175/JCLI3761.1
- Flato, G.M. (2005) The Third Generation Coupled Global Climate Model (CGCM3). http://www.ec.gc.ca/ccmac-cccma/default.asp?n=1299529F-1
- GFDL GAMDT (The GFDL Global Model Development Team) (2004) The New GFDL Global Atmospheric and Land Model AM2-LM2: Evaluation with Prescribed SST Simulations. Journal of Climate, 17, 4641-4673. http://dx.doi.org/10.1175/JCLI-3223.1
- Maurer, E.P., Wood, A.W., Adam, J.C., Lattenmaier, D.P. and Nijssen, B. (2002) A Long-Term Hydrologically-Based Dataset of Land Surface Fluxes and States for the Conterminous United States. Journal of Climate, 15, 3237-3251. http://dx.doi.org/10.1175/1520-0442(2002)015<3237:ALTHBD>2.0.CO;2
- Maurer, E.P., O’Donnell, G.M., Lattenmaier, D.P. and Roads, J.O. (2001) Evaluation of the Land Surface Water Budget in NCEP/NCAR and NCEP/DOE Reanalyses Using an Off-Line Hydrologic Model. Journal of Geophysical Research, 106, 17841-17862. http://dx.doi.org/10.1029/2000JD900828
- Maurer, E.P., Nijssen, B. and Lattenmaier, D.P. (2000) Use of the Reanalysis Land Surface Water Budget Variables in Hydrolic Studies. GEWEX News, 10, 6-8.
- Perkins, S.E., Pitman, A.J., Holbrook, N.J. and McAneney, J. (2007) Evaluation of the AR4 Climate Model’s Simulated Daily Maximum Temperature, Minimum Temperature, and Precipitation Over Australia Using Probability Density Functions. Journal of Climate, 20, 4356-4376. http://dx.doi.org/10.1175/JCLI4253.1
- Boberg, F., Berg, P., Thejill, P., Gutowski, W.J. and Christensen, J.H. (2010) Improved Confidence in Climate Change Projections of Precipitation Further Evaluated Using Daily Statistics from ENSEMBLES Models. Climate Dynamics, 35, 1509-1520. http://dx.doi.org/10.1007/s00382-009-0683-8
- Easterling, W.E., Weiss, A., Hays, C.J. and Mearns, L.O. (1998) Spatial Scales of Climate Information for Simulating Wheat and Maize Productivity: The Case of the US Great Plains. Agricultural and Forest Meteorology, 90, 51-63. http://dx.doi.org/10.1016/S0168-1923(97)00091-9
- Jha, M., Pan, Z., Takle, E.S. and Gu, R. (2004) Impacts of Climate Change on Streamflow in the Upper Mississippi River Basin: A Regional Climate Model Perspective. Journal of Geophysical Research, 109, D09105. http://dx.doi.org/10.1029/2003JD003686
- Willmott, C.J., Robeson, S.M. and Matsuura, K. (2012) Short Communication: A Refined Index of Model Performance. International Journal of Climatology, 32, 2088-2094. http://dx.doi.org/10.1002/joc.2419
- Brankovic, C. and Palmer, T.N. (1997) Atmospheric Seasonal Predictability and Estimates of Ensemble Site. Monthly Weather Review, 125, 859-874. http://dx.doi.org/10.1175/1520-0493(1997)125<0859:ASPAEO>2.0.CO;2
- Koo, G.-S., Boo, K.-O. and Kwon, W.-T. (2009) Projections of Temperature over Korea Using an MM5 Regional Climate Simulation. Climate Research, 40, 241-248. http://dx.doi.org/10.3354/cr00825
- Jupp, T.E., Cox, P.M., Ramming, A., Thonicke, K., Lucht, W. and Cramer, W. (2010) Development of Probability Density Functions for Future South America Rainfall. New Phytologist, 187, 682-693. http://dx.doi.org/10.1111/j.1469-8137.2010.03368.x
- Dai, A. (2001) Global Precipitation and Thunderstorm Frequencies. Part I: Seasonal and Interannual Variations. Journal of Climate, 14, 1092-1111. http://dx.doi.org/10.1175/1520-0442(2001)014<1092:GPATFP>2.0.CO;2
- Sun, Y., Solomon, S., Dai, A. and Portman, R.W. (2006) How Often Does It Rain? Journal of Climate, 19, 916-934. http://dx.doi.org/10.1175/JCLI3672.1
- Maxino, C.C., McAvaney, B.J., Pitman, A.J. and Perkins, S.E. (2008) Ranking the AR4 Climate Models over the Murray-Darling Basin Using Simulated Maximum Temperature, Minimum Temperature and Precipitation. International Journal of Climatology, 28, 1097-1112. http://dx.doi.org/10.1002/joc.1612
- Pitman, A.J. and Perkins, S.E. (2009) Global and Regional Comparison of Daily 2-m and 1000-hPa Maximum and Minimum Temperatures in Three Global Reanalyses. Journal of Climate, 22, 4667-4681. http://dx.doi.org/10.1175/2009JCLI2799.1
- Perkins, S.E. (2009) Smaller Projected Increases in 20-Year Temperature Returns over Australia in Skill-Selected Climate Models. Geophysical Research Letters, 36, L06710. http://dx.doi.org/10.1029/2009GL037293
- Perkins, S.E., Irving, D.B., Brown, J.R., Power, S.B., Moise, A.F., Colman, R.A. and Smith, I. (2012) CMIP3 Ensemble Climate Projections over the Western Tropical Pacific Based on Model Skill. Climate Research, 51, 35-58. http://dx.doi.org/10.3354/cr01046
- Willmott, C.J. and Wicks, D.E. (1980) An Empirical Method for the Spatial Interpolation of Monthly Precipitation Within California. Physical Geography, 1, 59-73.
- Willmott, C.J. (1981) On the Validation of Models. Physical Geography, 2, 184-194.
- Nash, J.E. and Sutcliffe, J.V. (1970) River Flow Forecasting Through Conceptual Models Part I: A Discussion of Prinicples. Journal of Hydrology, 10, 282-290. http://dx.doi.org/10.1016/0022-1694(70)90255-6
- Watterson, I.G. (1996) Non-Dimensional Measures of Climate Model Performance. International Journal of Climatology, 16, 379-391. http://dx.doi.org/10.1002/(SICI)1097-0088(199604)16:4<379::AID-JOC18>3.0.CO;2-U
- Legates, D.R. and McCabe Jr., G.J. (1999) Evaluating the Use of “Goodness-of-Fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resources Research, 35, 233-241. http://dx.doi.org/10.1029/1998WR900018
- Mielke, P.W. and Berry, K.J. (2001) Permutation Methods: A Distance Function Approach. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4757-3449-2
- Murphy, A.H. and Epstein, E.S. (1989) Skill Scores and Correlation Coefficients in Model Verification. Monthly Weather Review, 117, 572-581. http://dx.doi.org/10.1175/1520-0493(1989)117<0572:SSACCI>2.0.CO;2
- Huffman, G.J. (1997) Estimates of Root-Mean-Square Random Error for Finite Samples of Estimated Precipitation. Journal of Applied Meteorology, 36, 1191-1201. http://dx.doi.org/10.1175/1520-0450(1997)036<1191:EORMSR>2.0.CO;2
- Yang, Z. and Arritt, R.W. (2002) Test of Perturbed Physics Ensemble Approach for Regional Climate Modeling. Journal of Climate, 15, 2881-2896. http://dx.doi.org/10.1175/1520-0442(2002)015<2881:TOAPPE>2.0.CO;2
- Wu, H., Hubbard, K.G. and You, J. (2005) Some Concerns When Using Data from the Cooperative Weather Station Networks: A Nebraska Case Study. Journal of Atmospheric and Oceanic Technology, 22, 592-602. http://dx.doi.org/10.1175/JTECH1733.1
- Wilks, D.S. (2006) Statistical Methods in the Atmospheric Sciences. 2nd Edition, Academic Press, London.
- Liu, M., Kim, Y.-J. and Zhao, Q. Zhao (2012) Numerical Experiments of an Advanced Radiative Transfer Model in the U.S. Navy Operational Global Atmospheric Prediction System. Journal of Applied Meteorology and Climatology, 51, 554-570. http://dx.doi.org/10.1175/JAMC-D-11-018.1
- vonStorch, H. and Zwiers, F.W. Zwiers (1999) Statistical Analysis in Climate Research. Cambridge University Press, New York.
- Stull, R.B. (2000) Meteorology for Scientists and Engineers. 2nd Edition, Brooks/Cole Thomson Learning, Pacific Grove.
- Willmott, C.J. and Matsuura, K. (2005) Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Climate Research, 30, 79-82. http://dx.doi.org/10.3354/cr030079
- Freidenreich, S.M. and Ramaswamy, V. (2011) Analysis of the Biases in the Downward Shortwave Surface Flux in the GFDL CM2.1 General Circulation Model. Journal of Geophysical Research, 116, D08208. http://dx.doi.org/10.1029/2010JD014930
- Randall, D.A., Wood, R.A., Bony, S., Colman, R., Fichefet, T., Fyfe, J., Kattsov, V., Pitman, A., Shukla, J., Srinvasan, J., Stouffer, R. J., Sumi, A. and Taylor, K.E. (2007) Climate Models and Their Evaluation. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge.
- John, V.O. and Soden, B.J. (2007) Temperature and Humidity Biases in Global Climate Models and Their Impact on Climate Feedbacks. Geophysical Research Letters, 34. http://dx.doi.org/10.1029/2007GL030429
- Novick, K.A., Oren, R., Stoy, P.C., Siqueira, M.B.S. and Katul, G.G. (2009) Nocturnal Evaportranspiration in Eddy- Covariance Records from Three Co-Located Ecosystems in the Southeastern U.S.: Implications for Annual Fluxes. Agricultural and Forest Meteorology, 149, 1491-1504.
- Trenberth, K.E. (2008) The Impact of Climate Change and Variablility on Heavy Precipitation, Floods, and Droughts, The Encycolpedia of Hydrological Sciences. John Wiley & Sons, Ltd., Chichester.
- Solman, S.A., Nunez, M.N. and Cabre, M.F. (2008) Regional Climate Change Experiments over Southern South America. I: Present Climate. Climate Dynamics, 30, 533-552. http://dx.doi.org/10.1007/s00382-007-0304-3
- Min, S.-K., Zhang, X., Zwiers, F.W. and Hegerl, G.C. (2011) Human Contribution to More-Intense Precipitation Extremes. Nature, 470, 378-381. http://dx.doi.org/10.1038/nature09763
- Samenow, J. (2012) U.S. Had Most Extreme Precipitation on Record in 2011. The Washington Post, 12 January 2012. http://www.washingtonpost.com/blogs/capital-weather-gang/post/us-had-most-extreme-precipitation-on-record-in-2011/2012/01/11/gIQA7oJXrP_blog.html





















