International Journal of Modern Nonlinear Theory and Application
Vol.2 No.4(2013), Article ID:41231,3 pages DOI:10.4236/ijmnta.2013.24035
Inverse Scattering Problem for the Schrödinger’s Equation
Buketov Karaganda State University, Karaganda, Kazakhstan
Email: aset.durmagambet@gmail.com
Copyright © 2013 Asset A. Durmagambetov, Leyla S. Fazilova. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 11, 2013; revised December 11, 2013; accepted December 18, 2013
Keywords: Schrödinger’s Equation; Potential; Scattering Amplitude
ABSTRACT
The analytic properties of the scattering amplitude are discussed. And, the representation of the potential by the scattering amplitude is obtained.
1. Introduction
We consider that the operators ,
, 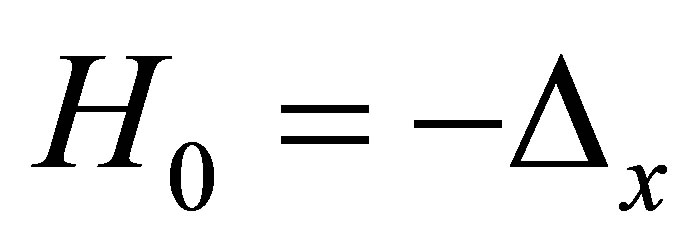 are defined in the dense set
are defined in the dense set 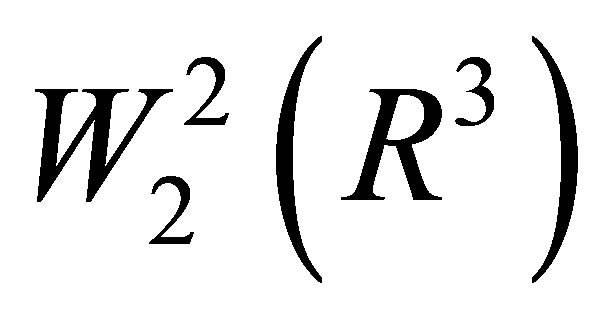 in the space
in the space 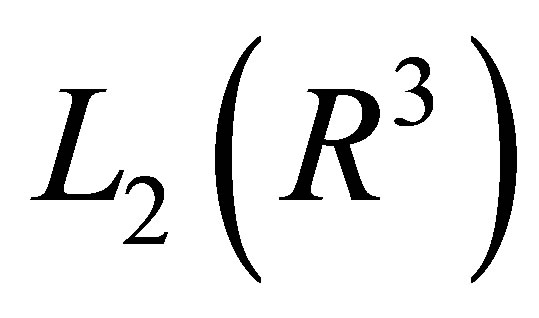 and that
and that  is a bounded fast-decreasing function. The operator
is a bounded fast-decreasing function. The operator  is called Schrödinger’s operator.
is called Schrödinger’s operator.
We consider the three-dimensional inverse scattering problem for the Schrödinger’s operator: the scattering potential has to be reconstructed from scattering amplitude. This problem has been studied by a number of researchers (in [1-3] and references therein).
2. Results
We consider Schrödinger’s equation:
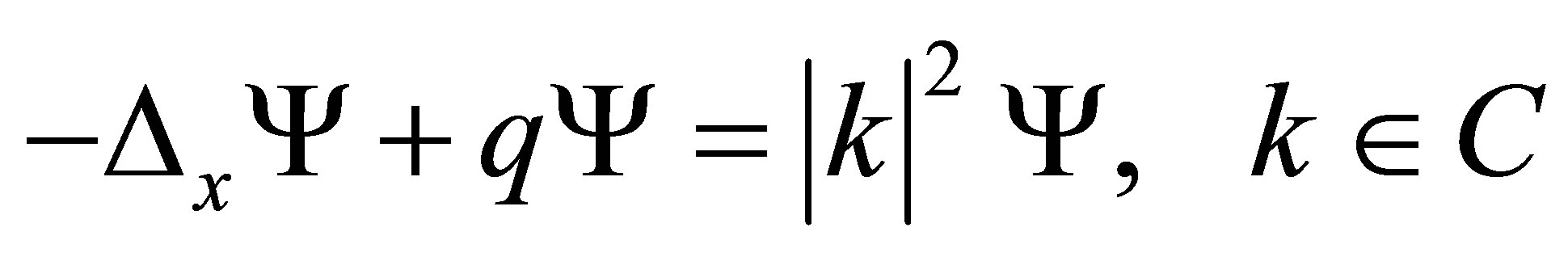 (1)
(1)
Let 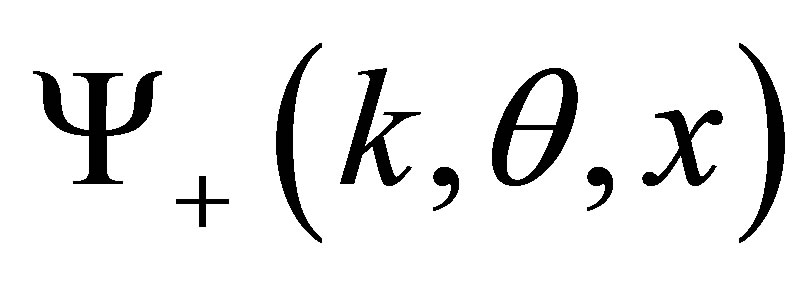 is a solution of the (1) with the following asympotic behavior:
is a solution of the (1) with the following asympotic behavior:
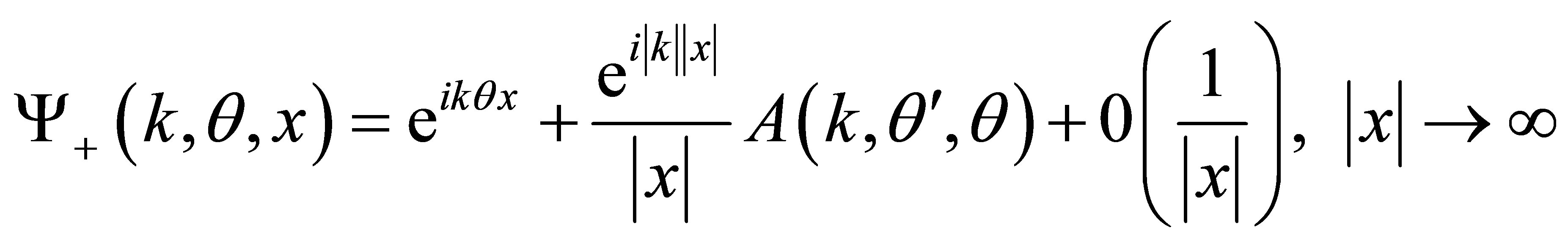 (2)
(2)
where 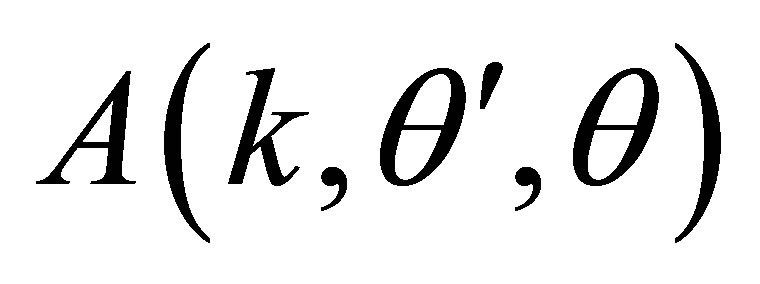 scattering amplitude, and
scattering amplitude, and
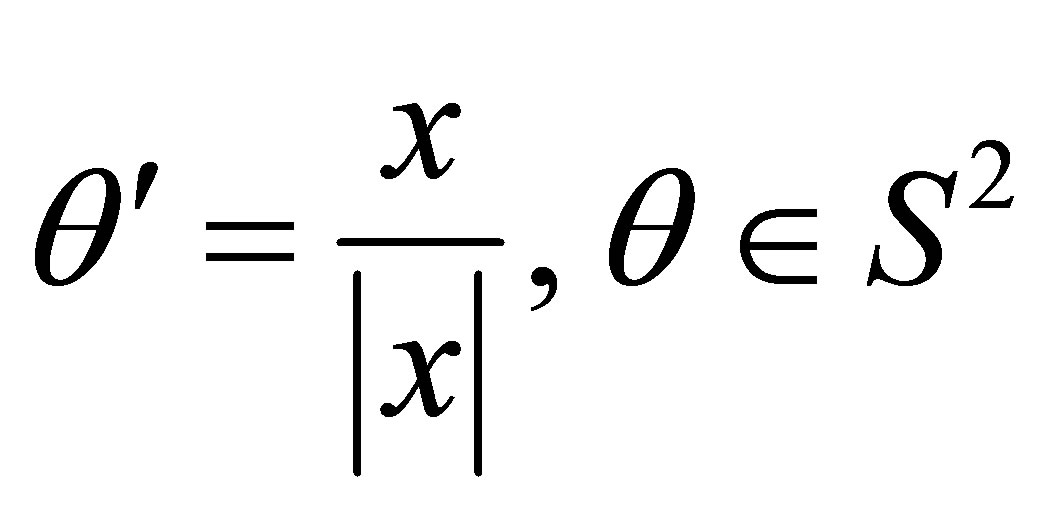 , for
, for 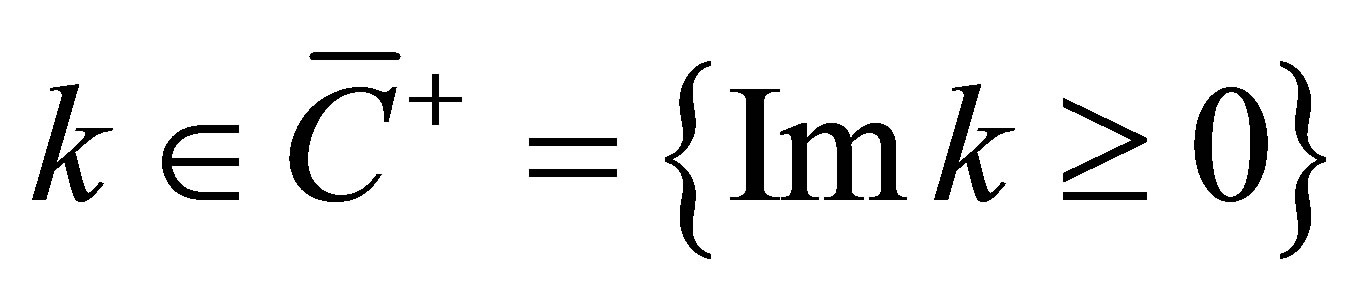
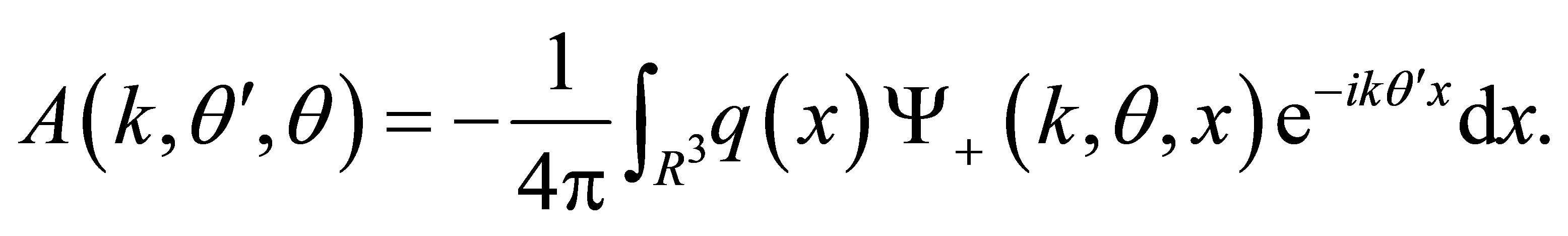 (3)
(3)
We also define the solution , for
, for
 as
as .
.
As well known [1]:
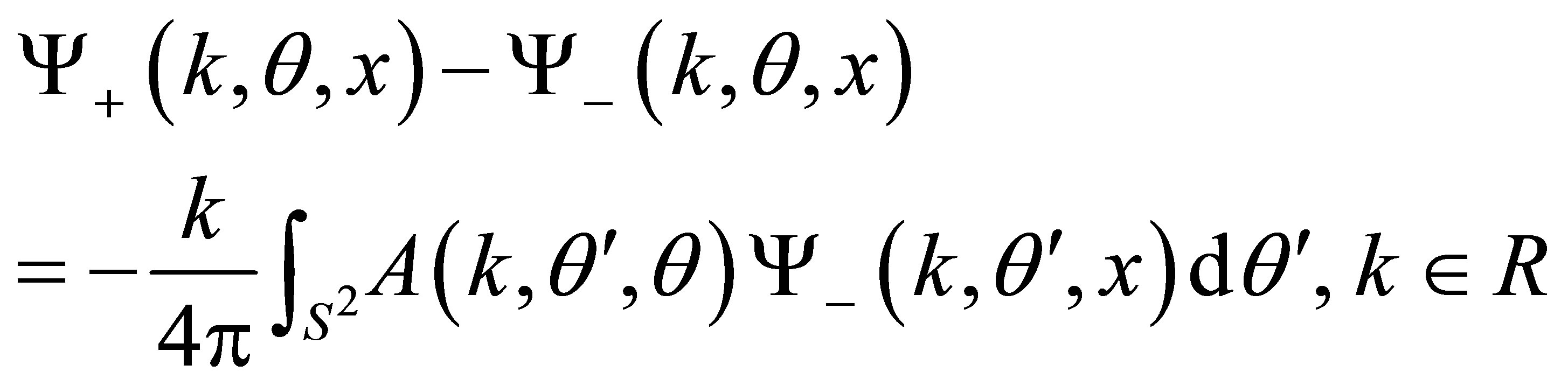 (4)
(4)
This equation is the key to solving the inverse scattering problem, and was first used by R. G. Newton in [2,3] and E. Somersalo et al. in [4].
Equation (4) is equivalent to the following:
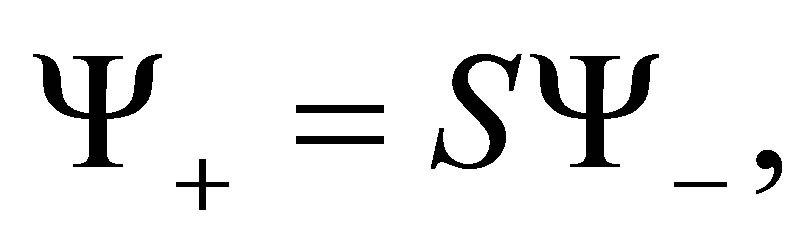 (5)
(5)
where 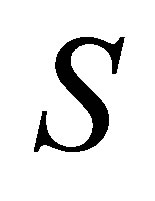 is a scattering operator with the kernel
is a scattering operator with the kernel ,
, 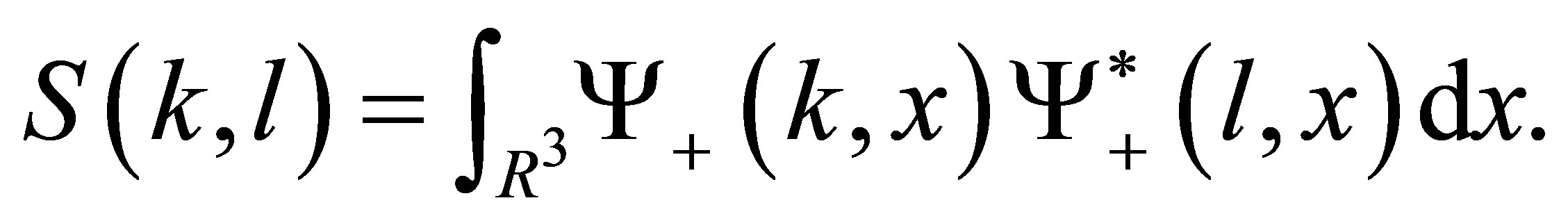
Here is a theorem according to [1]:
Theorem 1 (The energy and momentum conservation laws)
Let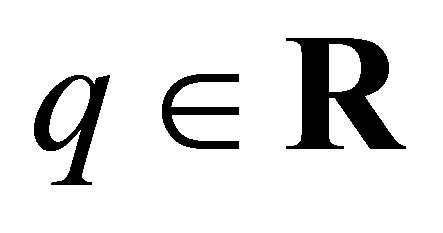 , then
, then 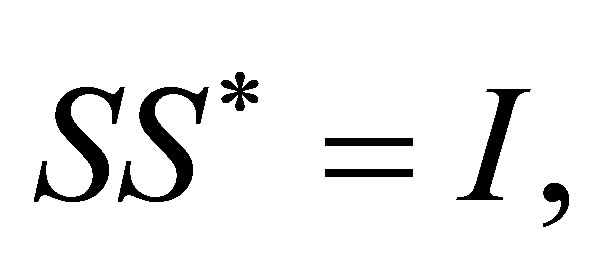
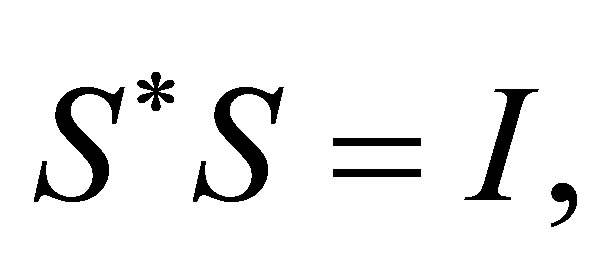 where
where  is a unitary operator.
is a unitary operator.
Definition 1 The set of measurable functions  with the norm, defined as
with the norm, defined as 
is recognized as Rollnik’ class.
As shown in [5], 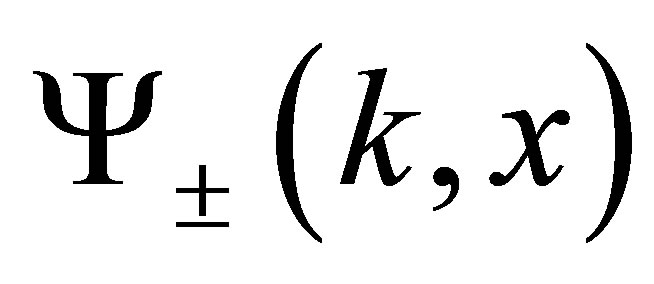 is an orthonormal system of
is an orthonormal system of  eigenfunctions for the continuous spectrum. In addition to the continuous spectrum there are a finite number
eigenfunctions for the continuous spectrum. In addition to the continuous spectrum there are a finite number  of
of  negative eigenvalues, designated as
negative eigenvalues, designated as 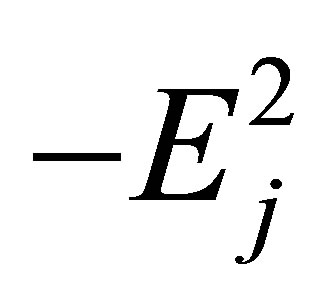 with corresponding normalized eigenfunctions
with corresponding normalized eigenfunctions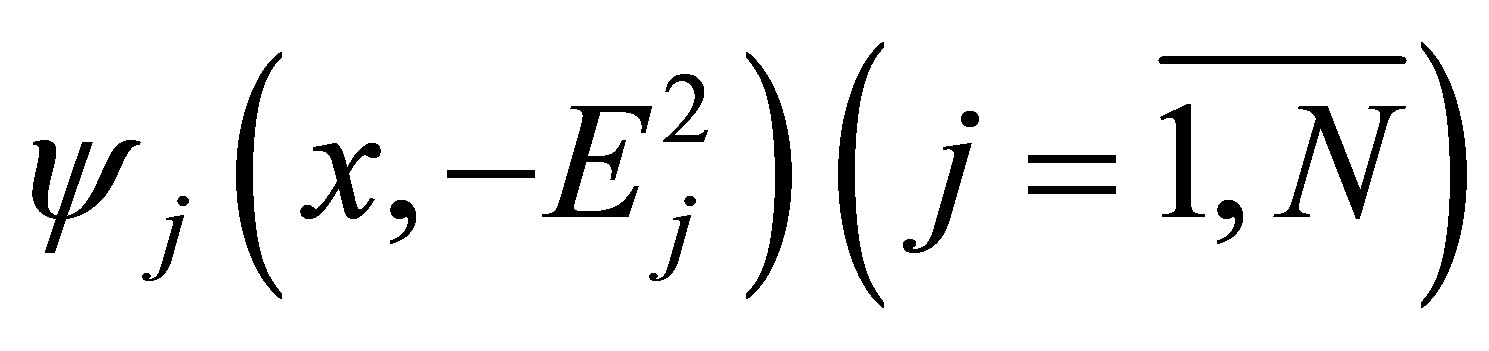 , where
, where .
.
We present Povzner’s results [5] below:
Theorem 2 (Completness) Both for arbitrary 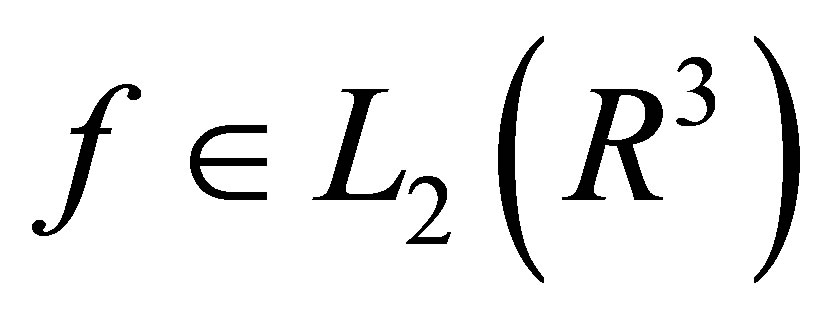 and for
and for  eigenfunctions Parseval’s identity is valid.
eigenfunctions Parseval’s identity is valid.
 (6)
(6)
where 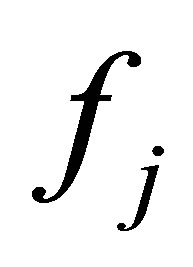 and
and 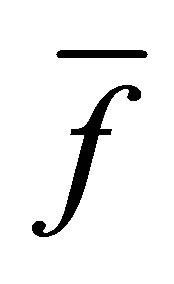 are Fourier coefficients for continuous and dicrete cases.
are Fourier coefficients for continuous and dicrete cases.
Theorem 3 (Birmann-Schwinger estimation). Let . Then number of discrete eigenvalues can be estimated as:
. Then number of discrete eigenvalues can be estimated as:
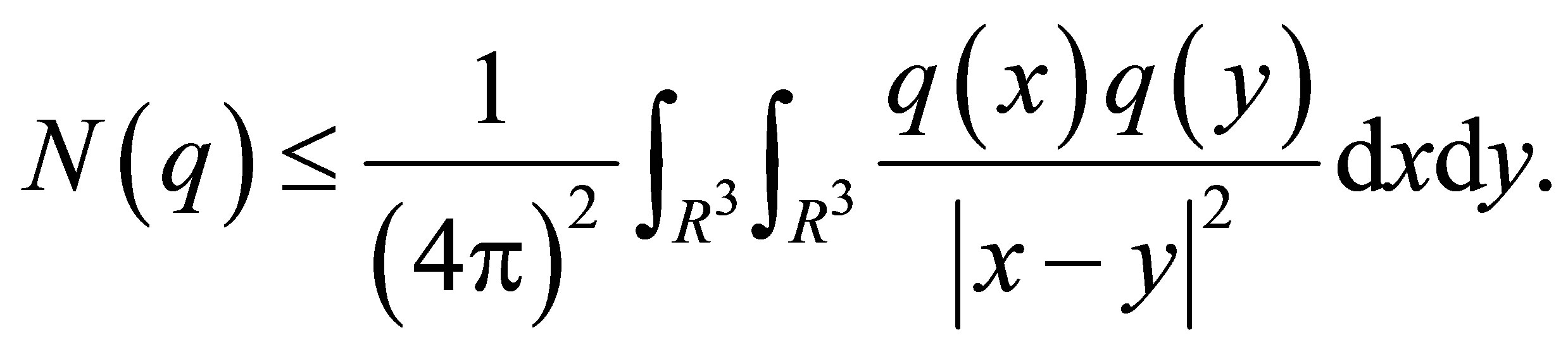 (7)
(7)
The theorem was proved in [6].
Let introduce the following notation:
 (8)
(8)
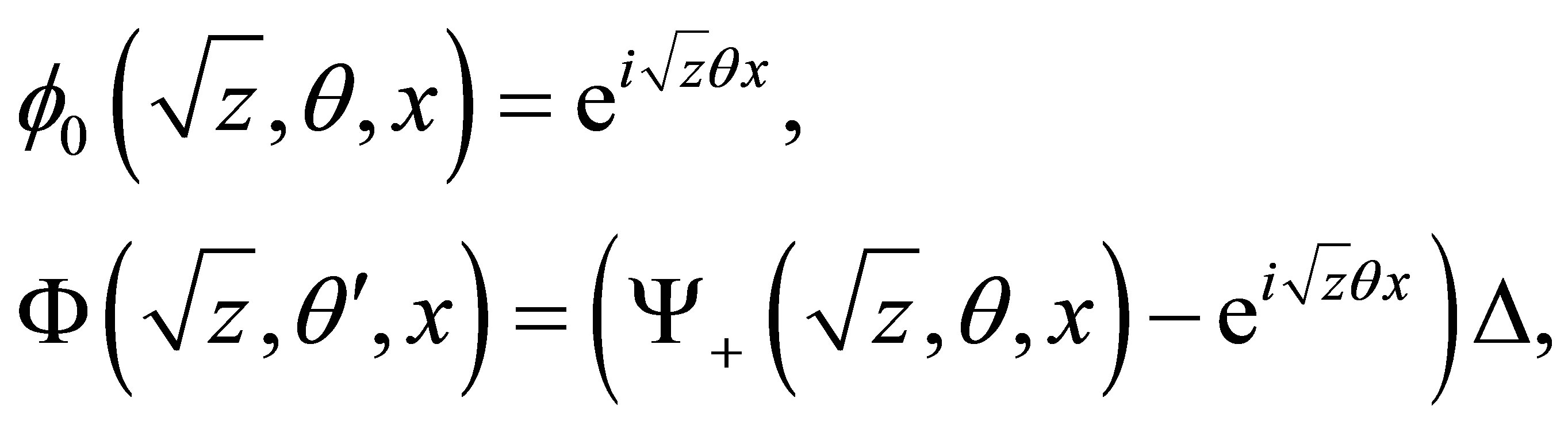 (9)
(9)
where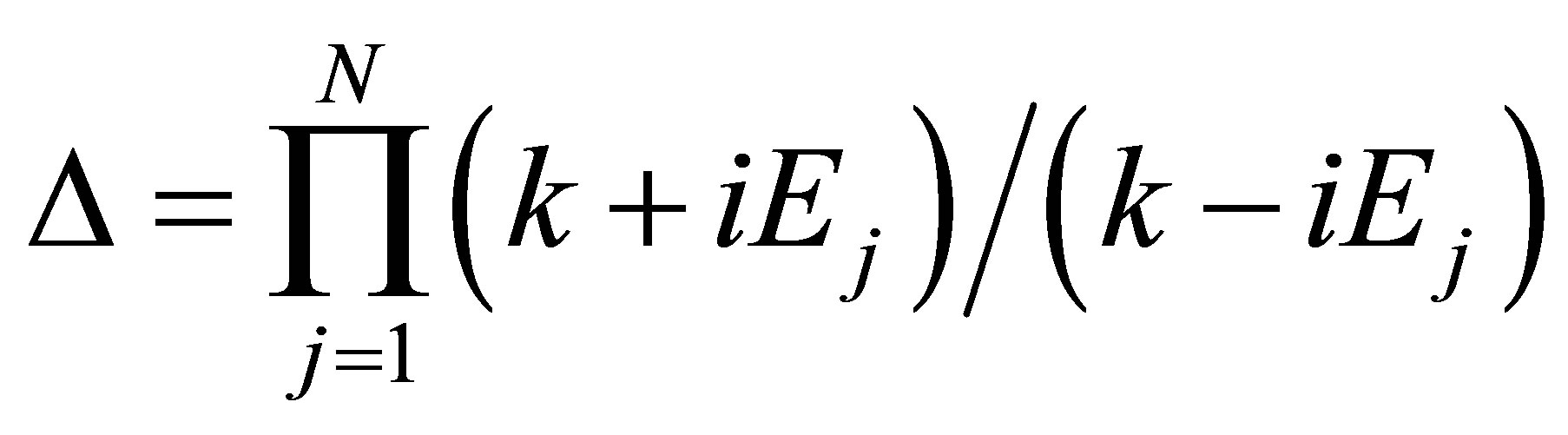 . Define the operators
. Define the operators
 ,
, 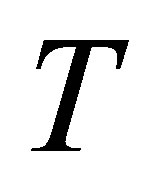 for
for  as follows:
as follows:
 (10)
(10)
 (11)
(11)
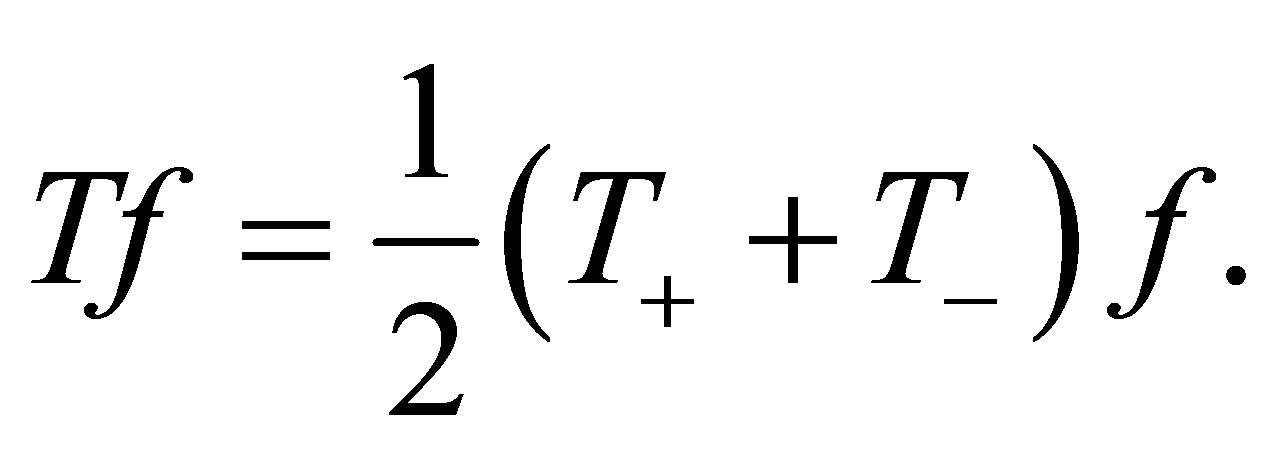 (12)
(12)
We consider the Riemann problem of finding a function , which is analytic in the complex plane with cut along the real axis.
, which is analytic in the complex plane with cut along the real axis.  values on the sides of the cat are denoted as
values on the sides of the cat are denoted as ,
,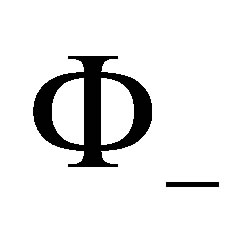 . Below present the results of [7].
. Below present the results of [7].
Lemma 1
 (13)
(13)
Theorem 4 Let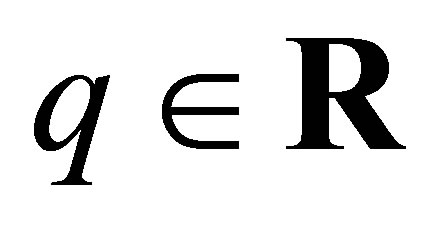 ,
,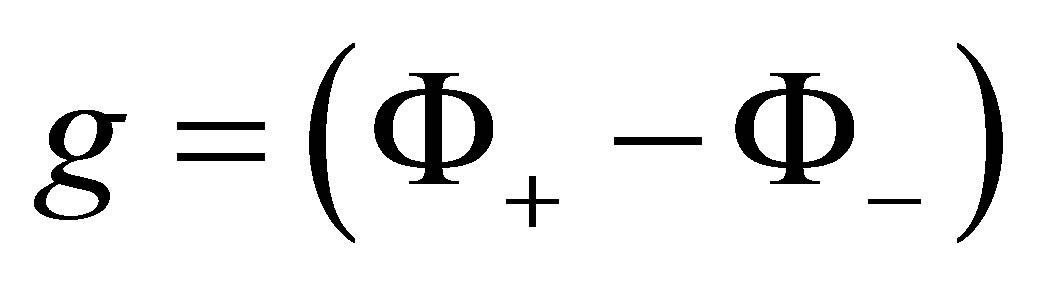 . Then
. Then
 (14)
(14)
The proof of the above follows from the classic results on the Riemann problem.
Lemma 2 Let 
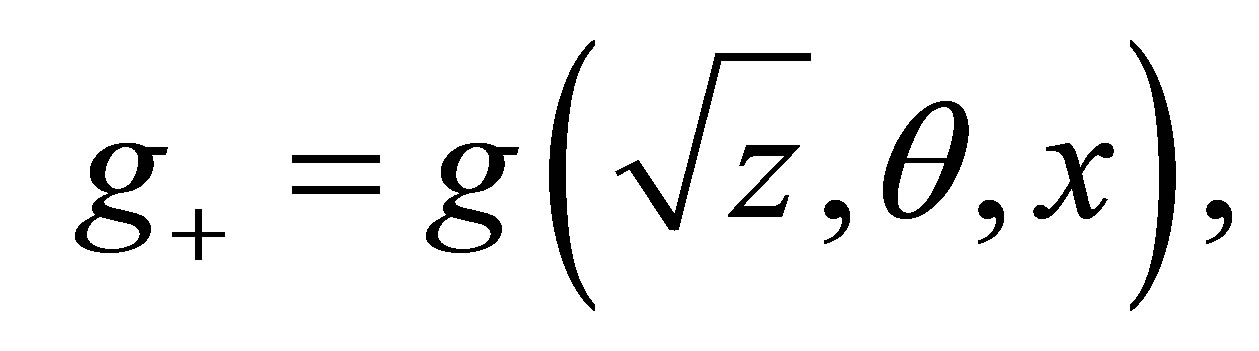
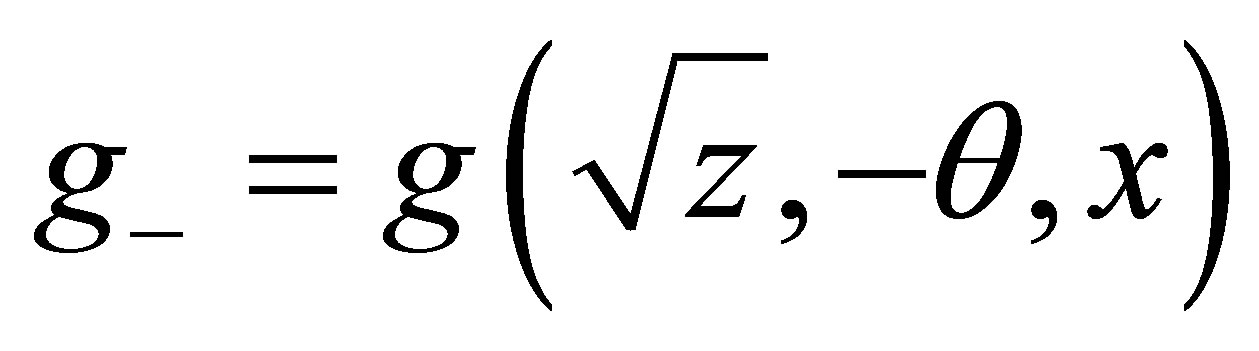 , then
, then
 (15)
(15)
The proof of the above follows from the definitions of 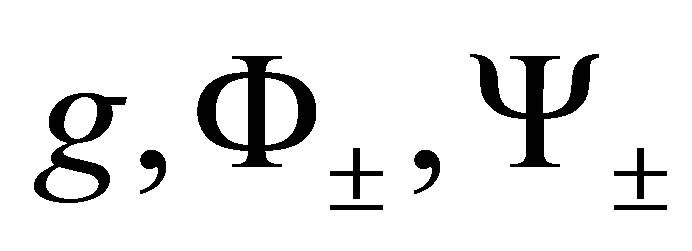 functions.
functions.
Lemma 3 Let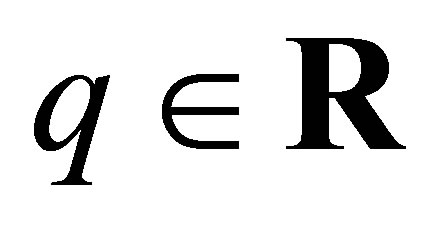 ,
,
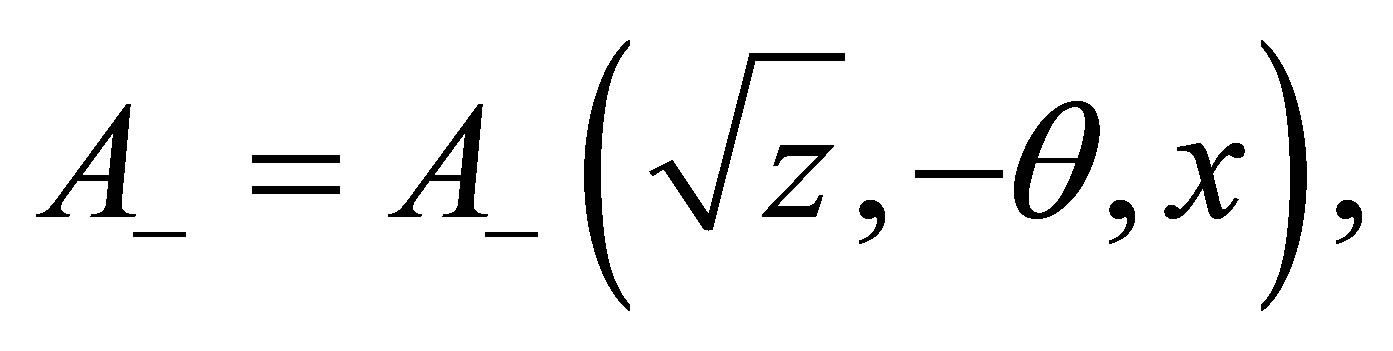
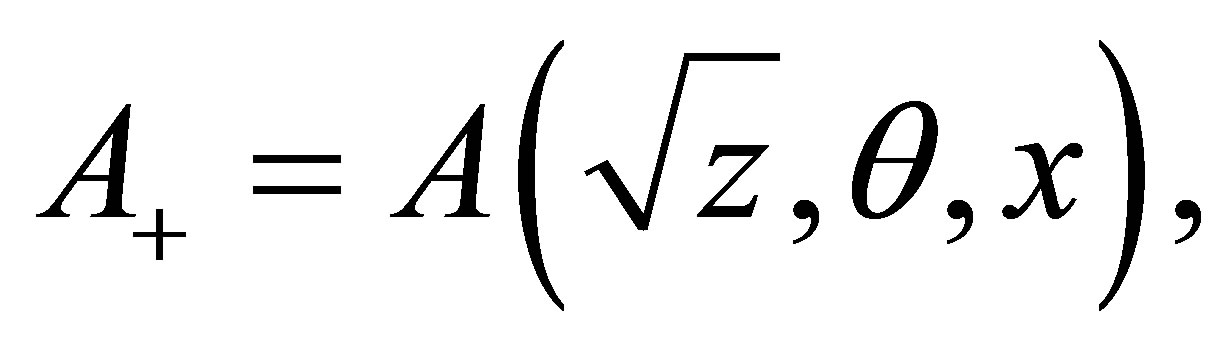 then
then
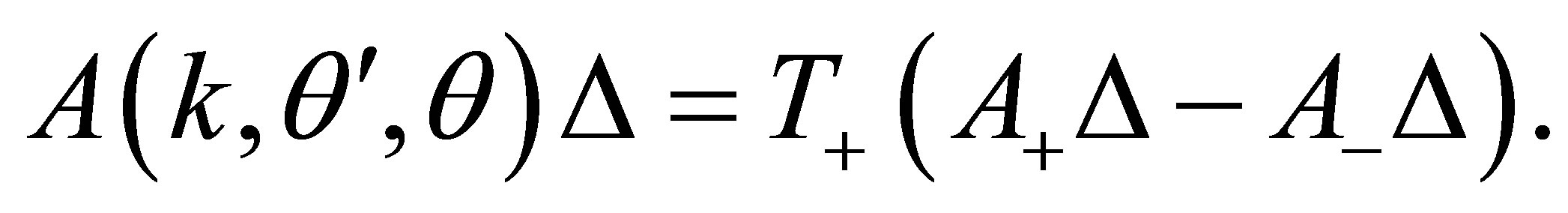 (16)
(16)
The proof of the above follows from the definitions of 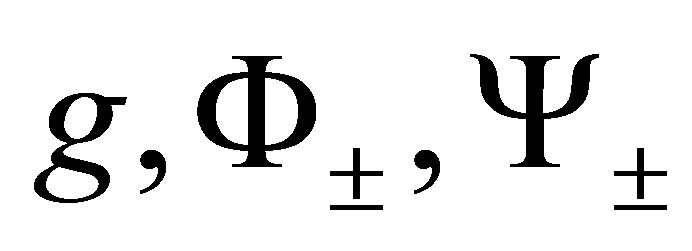 functions.
functions.
Lemma 4 Let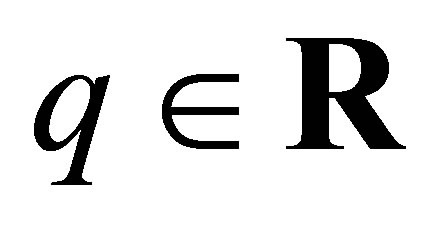 , then
, then
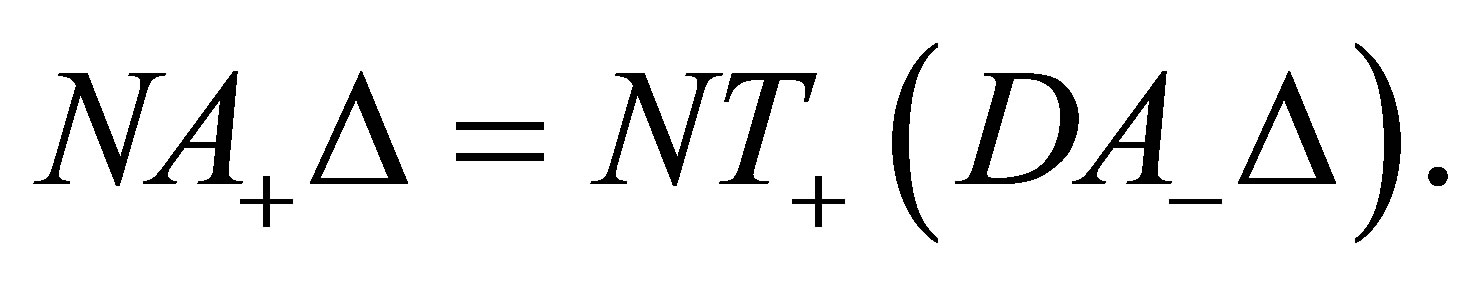 (17)
(17)
The proof of the above follows from the definitions of 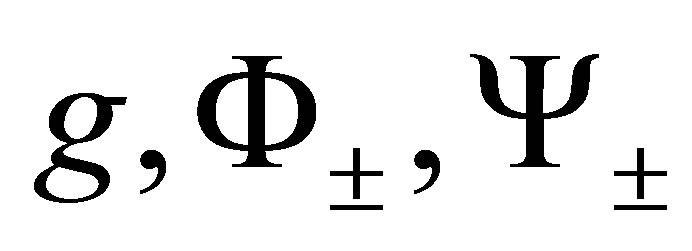 functions and Theorem 1.
functions and Theorem 1.
Definition 2 Denote by  the set of functions
the set of functions 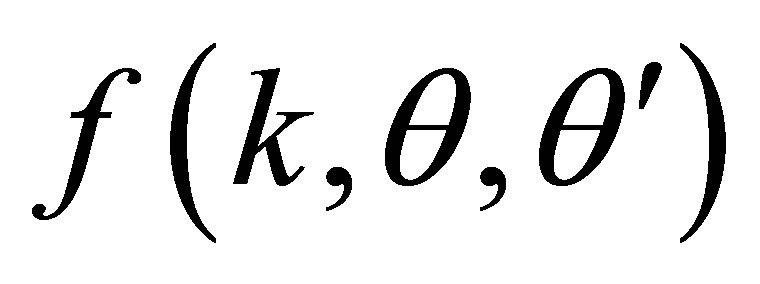 with the norm
with the norm

Definition 3 Denote by 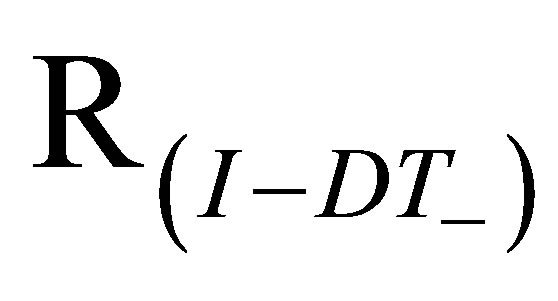 the set of functions g such that
the set of functions g such that
 .
. Lemma 5 Suppose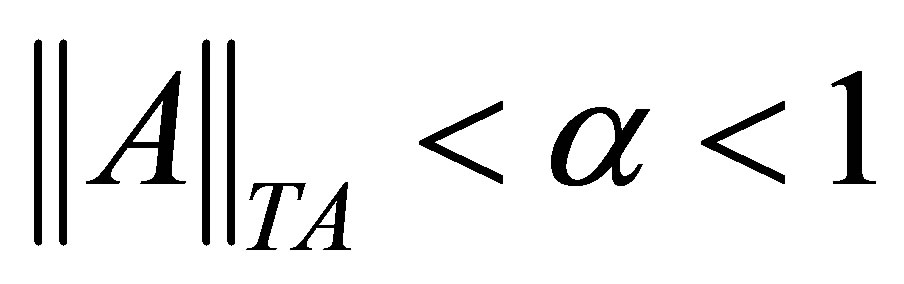 then the operator
then the operator 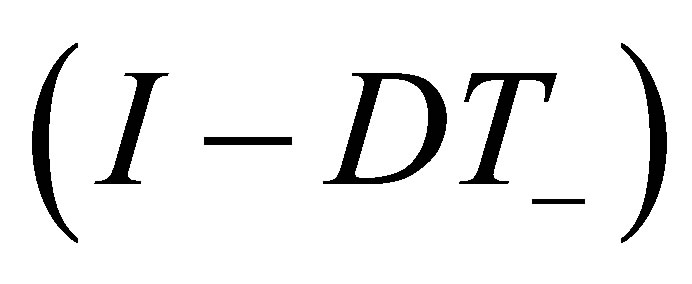 defined on the set
defined on the set  has inverse defined on the
has inverse defined on the .
.
The proof of the above follows from the definitions of 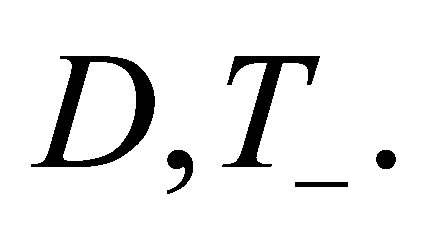 and conditions Lemma 5
and conditions Lemma 5
Lemma 6 Let 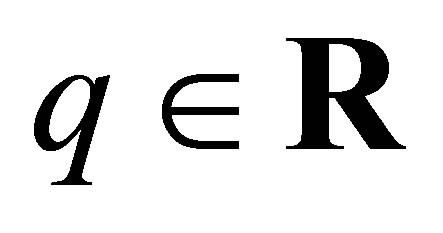 and
and 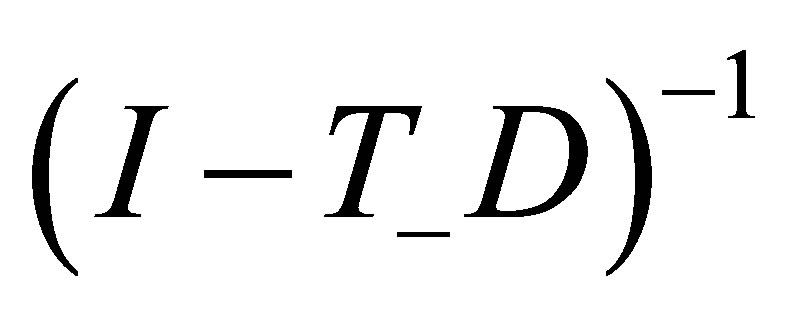 is existing. Then
is existing. Then
 (18)
(18)
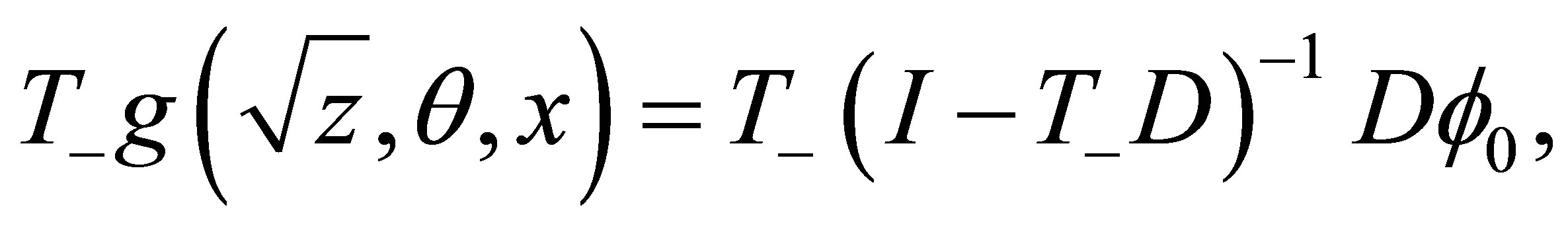 (19)
(19)
 (20)
(20)
The proof of the above follows from the definitions of 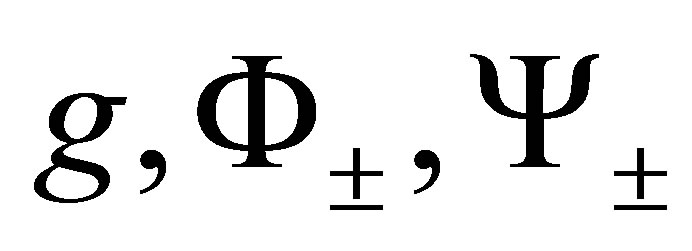 functions and Equation (4)
functions and Equation (4)
Lemma 7 Let . Then
. Then
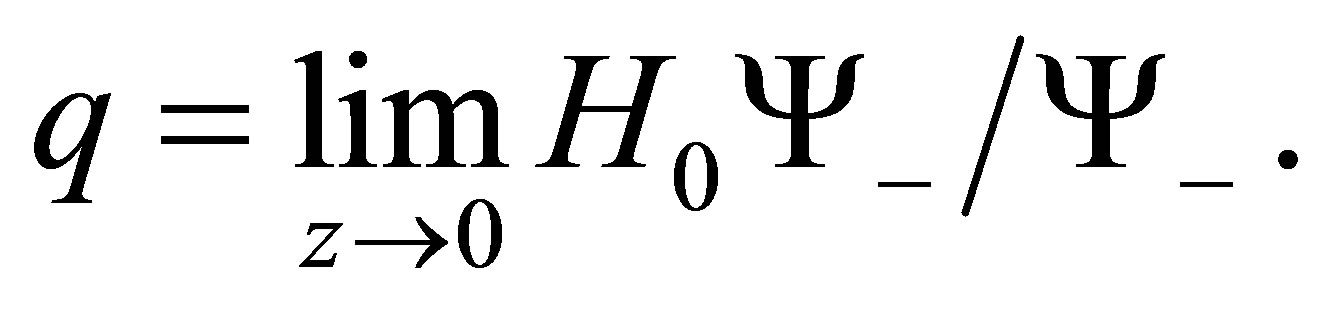 (21)
(21)
The lemma can be proved substituting 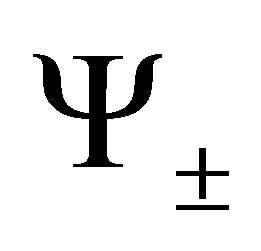 in Equation (1).
in Equation (1).
Lemma 8 Let , and
, and 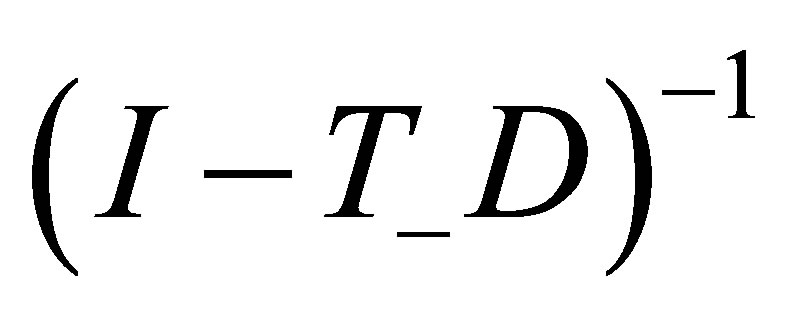 is existing. Then
is existing. Then
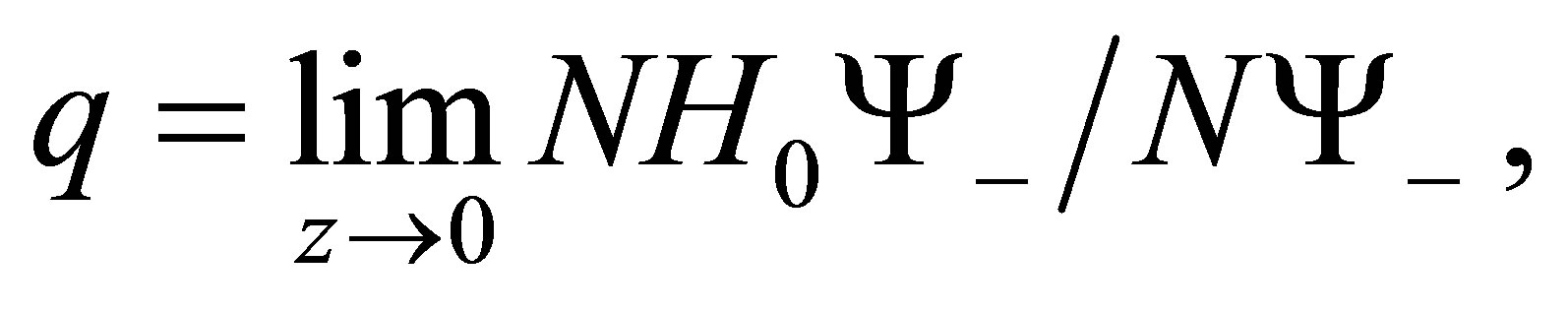 (22)
(22)

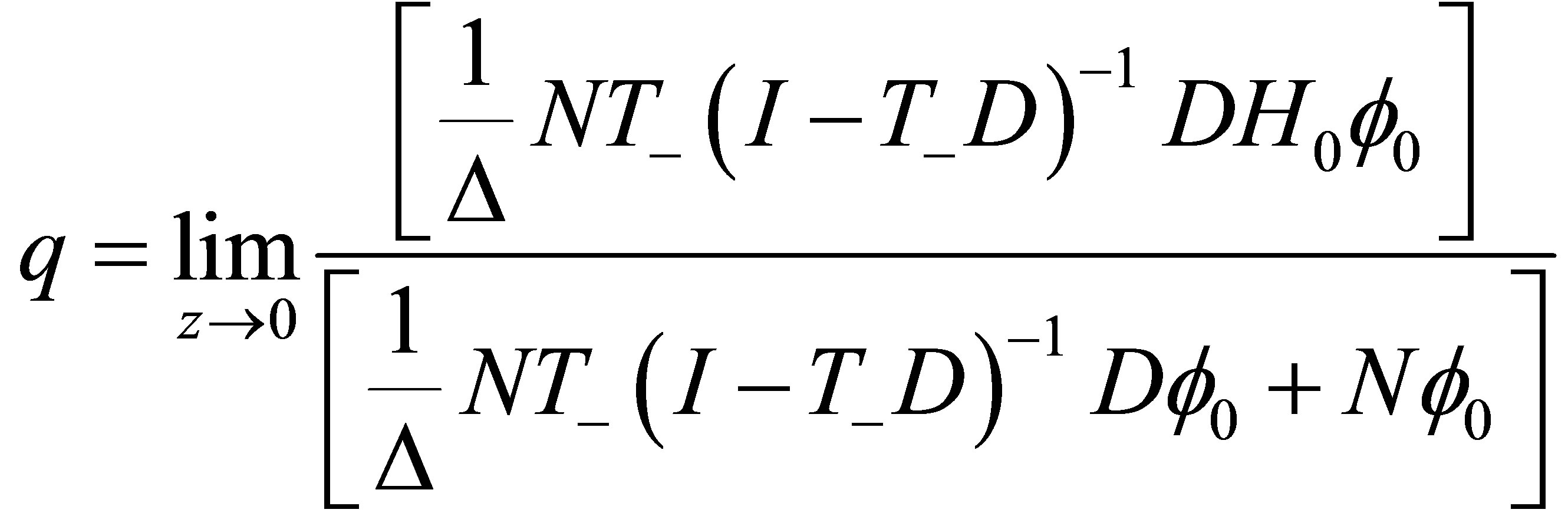 (23)
(23)
The proof of the above follows from the definitions of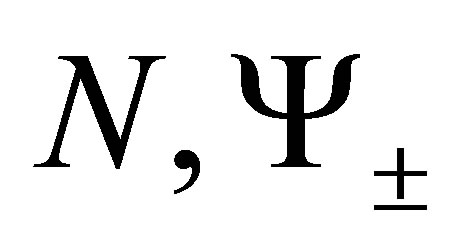 , Lemma 6, Lemma 7.
, Lemma 6, Lemma 7.
3. Conclusion
This study has shown once again the outstanding properties of the scattering operator, which allow, in combination with analytical properties of the wave function, obtaining the almost explicit formulas for the potential from the scattering amplitude. Furthermore, this approach allows solving the problem of over-determination, resulting from the fact that the potential is a function of three variables, whereas the amplitude is a function of five variables. We have shown that it is sufficient to average the scattering amplitude to eliminate the two extra variables.
4. Acknowledgements
We thank the Ministry of Education and Science of the Republic of Kazakhstan for a grant, and the “Factor” Company of System Researches for combining our efforts in this project.
The work was performed as a part of the international project “Joint Kazakh-Indian study the influence of anthropogenic factors on atmospheric phenomena on the basis of numerical weather prediction models WRF (Weather Research and Forecasting)”, commissioned by the Ministry of Education and Science of the Republic of Kazakhstan.
、References
[1] L. D Faddeev, “Inverse Problem of Quantum Scattering Theory II,” Itogi Nauk Takh. Sov Probl Mat, Vol. 3, 1974, p. 93-180.
[2] R. G. Newton, “New Result on the Inverse Scattering Problem in Three Dimensions,” Physical Review Letters, Vol. 43, No. 8, 1979, pp. 541-542.
[3] R. G. Newton, “Inverse Scattering Three Dimensions,” Journal of Mathematical Physics, Vol. 21, No. 7, 1980, pp. 1698-1715. http://dx.doi.org/10.1063/1.524637
[4] E. Somersalo, et al., “Inverse Scattering Problem for the Schrodinger’s Equation in Three Dimensions: Connections between Exact and Approximate Methods,” 1988.
[5] A. Y. Povzner, “On the Expansion of Arbitrary Functions in Characteristic Functions of the Operator 
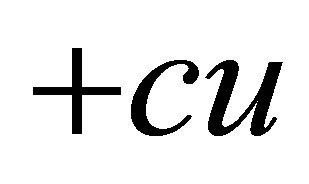 ,” Matematicheskii Sbornik, Vol. 32, No. 74, 1953, pp. 109- 156.
,” Matematicheskii Sbornik, Vol. 32, No. 74, 1953, pp. 109- 156.
[6] M. Birman, “On the Spectrum of Singular BoundaryValue Problems,” (Russian) Matematicheskii Sbornik, Vol. 55, No. 97, 1961, pp. 125-174.
[7] H. Poincare, “Lecons de Mecanique Celeste,” 1910.

