Open Journal of Fluid Dynamics
Vol.06 No.04(2016), Article ID:72977,20 pages
10.4236/ojfd.2016.64028
Diffusion Process of High Concentration Spikes in a Quasi-Homogeneous Turbulent Flow
Masaya Endo, Qianqian Shao, Takahiro Tsukahara, Yasuo Kawaguchi
Department of Mechanical Engineering, Tokyo University of Science, Chiba, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 14, 2016; Accepted: December 23, 2016; Published: December 26, 2016
ABSTRACT
When a mass spreads in a turbulent flow, areas with obviously high concentration of the mass compared with surrounding areas are formed by organized structures of turbulence. In this study, we extract the high concentration areas and investigate their diffusion process. For this purpose, a combination of Planar Laser Induced Fluorescence (PLIF) and Particle Image Velocimetry (PIV) techniques was employed to obtain simultaneously the two fields of the concentration of injected dye and of the velocity in a water turbulent channel flow. With focusing on a quasi-homogeneous turbulence in the channel central region, a series of PLIF and PIV images were acquired at several different downstream positions. We applied a conditional sampling technique to the PLIF images to extract the high concentration areas, or spikes, and calculated the conditional-averaged statistics of the extracted areas such as length scale, mean concentration, and turbulent diffusion coefficient. We found that the averaged length scale was constant with downstream distance from the diffusion source and was smaller than integral scale of the turbulent eddies. The spanwise distribution of the mean concentration was basically Gaussian, and the spanwise width of the spikes increased linearly with downstream distance from the diffusion source. Moreover, the turbulent diffusion coefficient was found to increase in proportion to the spanwise distance from the source. These results reveal aspects different from those of regular mass diffusion and let us conclude that the diffusion process of the spikes differs from that of regular mass diffusion.
Keywords:
Turbulent Transport, High Concentration Spikes, Quasi-Homogeneous Turbulent Flow, Conditional Sampling Technique, PIV and PLIF Measurements, Passive Scalar Diffusion

1. Introduction
Understanding the turbulent transport of passive scalar is very important in environmental flows where pollutants affect the safety and quality of our life. For instance, diffusion accidents have affected a large number of victims around the world, as in the Chernobyl Nuclear Power Plant disaster in 1986 and the Fukushima Daiichi Nuclear Power Plant in 2011. In such cases, a quick and accurate method of predicting pollutant diffusion is needed in order to prevent damages. As an example of prediction method for substance’s diffusion, the SPEEDI (System for Prediction of Environmental Emergency Dose Information) was applied when radioactive material was emitted from the Fukushima Daiichi Nuclear Power Plant [1] [2] [3] . For realization of the diffusion prediction, the diffusion theory in turbulent flows has been studied for many years. There are pioneering studies on the diffusion theory such as Taylor’s diffusion theory [4] and Richardson’s diffusion theory [5] . These theories reference the spreading width of a diffusing material released into homogeneous turbulence, revealing that the relationship between the increasing rate of the spreading width and the diffusion time depends on whether the diffusion time is smaller or larger than the time scale of eddies in the flow. The relationship has been investigated further with time-average scalar statistics including mean concentration, concentration fluctuation intensity and the turbulent diffusion coefficient by experimental and numerical methods [6] [7] [8] [9] . Owing to the progress of research on the diffusion theory, the diffusion prediction has become more accurate and speedy.
Mass distribution formed by spreading in a turbulent flow is usually called plume, and instantaneous concentration distribution fluctuates in both space and time. Fluid with an obviously high concentration compared with surrounding fluid can be observed. These areas may suffer great damage from turbulent mass diffusion such as the diffusing pollution caused by a sudden accident, and it is important to have a better understanding of the diffusion theory that relates to them. Such high concentration areas (called “high concentration spikes”, hereafter) are formed by organized structures of turbulence. Different from the mass plume which concerns whether there is non- zero concentration or not, the high concentration spikes emphasize two key points: one is the relatively high concentration in the spikes; the other is the large concentration gradients around the spikes. Considering the essential difference between the spikes and plumes, it is expected that the diffusion theory of the high concentration spikes will differ from that of the concentration plume. Several previous researches reported these spikes and their characteristics. The turbulent structure relating to the occurrence of the spikes was investigated in a grid turbulence and turbulent shear flow with a spatially uniform mean concentration gradient [10] [11] [12] [13] . The high concentration spikes occurred at a saddle point of the velocity field based on the large-scale structure of turbulent eddies. Moreover, according to [14] [15] , the occurrence frequency as well as the mean concentration of the high concentration spikes decreases with increasing distance downstream from the source. Although the high concentration spikes and their occurrence mechanism have attracted many researchers, those calculated statistics are not enough to derive a diffusion theory or prediction method regarding the high concentration spikes. Clarification of the diffusion theory of the high concentration spikes is an important challenge in reducing the damage from pollutant diffusion by means of a quick localization of the emission source.
In this paper, we worked out the basic diffusion theory of the high concentration spikes in a turbulent flow based on Taylor’s diffusion theory. Taylor’s diffusion theory deals with a suspended single particle emitted from a point source and assumes the homogeneous turbulence without any external body force such as buoyancy. With the aim of calculating the scalar statistics of high concentration spikes, which relate to the diffusion theory, we experimentally demonstrated the concentration and velocity fields of passive scalar (dye) diffusing from a fixed emission point in a quasi-homogeneous turbulent flow with simultaneous PIV (Particle Image Velocimetry) and PLIF (Planar Laser Induced Fluorescence) measurement. As a simple test case, we employed a water channel flow between two parallel walls. The high concentration spike we focus on in this study occurs intermittently in the turbulent flow, and its unconditional statistical quantities such as mean concentration and concentration fluctuation cannot be calculated by the normal ensemble-average operation. In order to extract the high concentration spikes, the conditional sampling technique [16] was applied to a spatial dye- diffusion image obtained by PLIF measurement. From the experimental results of the scalar statistics of the extracted spikes, which include spanwise diffusion width, average length scale, mean concentration, and turbulent diffusion coefficient, the diffusion theory of the spikes as well as its difference with that of the concentration plume were discussed.
2. Experimental Procedure
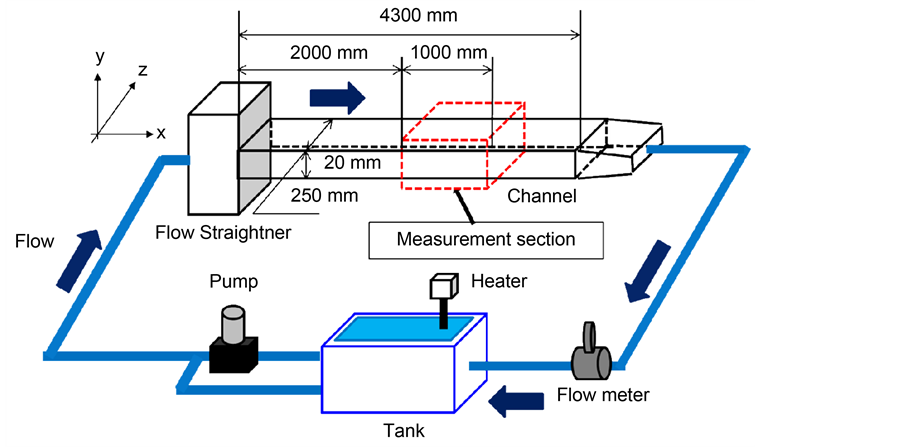
Figure 1 shows a schematic diagram of our main experimental apparatus, which was a closed-circuit water channel. The water flow under constant temperature was driven by an inverter controlled centrifugal pump with the constant volume. A rectifier was installed at the entrance to ensure a steady flow by damping the large vortices. The channel part including the measurement section was made of transparent acrylic resin for precise visualization and had a height of 20 mm (2δ), and a width of 250 mm (aspect ratio 12.5). A fully developed two-dimensional turbulent channel flow was established in the measurement section, which was located 2000 - 3000 mm downstream from the channel inlet. The flow rate Q was measured by a flow-meter to monitor the constant Reynolds number. The bulk Reynolds number was fixed at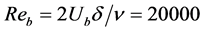 , where
, where 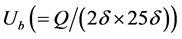 and ν denote the bulk velocity and the kinematic viscosity of water, respectively.
and ν denote the bulk velocity and the kinematic viscosity of water, respectively.
In this study, we focus on the statistically modeled quasi-homogeneous turbulence to investigate the fundamental characteristics of the high concentration spikes. Accordingly, the uniformities of the time-average velocity and turbulent intensity in the turbulent flow are important. Figure 2 shows the spanwise distributions of time-average streamwise velocity Uc and turbulent intensity 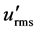 at the channel center obtained by PIV measurement. We can confirm that the velocity field in the measurement area was fully developed and the assumption of no velocity gradient in spanwise direction is
at the channel center obtained by PIV measurement. We can confirm that the velocity field in the measurement area was fully developed and the assumption of no velocity gradient in spanwise direction is
Figure 1. Experimental apparatus.
Figure 2. Spanwise distributions of time-average streamwise velocity and turbulent intensity at channel center obtained by PIV measurement.
acceptable. This means that the flow field we focus on in this study is quasi-homogeneous turbulence in the two-dimensional plane of the streamwise and spanwise directions. In order to measure the spatial velocity field and concentration field at the same time and at the same position, we employed simultaneous PIV and PLIF measurement.
This simultaneous measurement was extensively used to investigate the mixing processes [17] [18] [19] . Figure 3 shows the measurement section of simultaneous PIV and PLIF measurement. From the nozzle located at the center of the channel, a solution containing fluorescent dye was introduced into water flow for PLIF measurement. The water flow was laden with tracer particles for PIV measurement. The nozzle had an internal diameter of 1 mm and outside diameter of 2 mm. Both coordinate systems define x as the streamwise direction, z as the spanwise direction, y as the wall-normal direction, and the nozzle tip as the origin point. The injection speed of the dye solution was
Figure 3. Measurement section for simultaneous PIV and PLIF measurement.
controlled by a micro-syringe pump to be the same as the velocity of the local flow. We assumed that the amount volume of released dye solution was so small that any effect on the turbulence would be neglected. We used US-20S as the tracer particles, which are sufficiently small and can be assumed to faithfully follow the flow dynamically, and also used Rhodamine WT as the fluorescent dye, which exhibits a high Schmidt number of approximately 3000 in water. A laser emission device (Nd: YAG laser) was installed at the side of the channel while cameras to capture the light for measurement of velocity and concentration were installed below the channel. Alaser sheet with a wavelength of 532 nm was emitted to the height of the channel center after expanding to a plane with a thickness of 1 mm by a cylindrical lens. With laser illumination, scattering light from the tracer particles with a wavelength of 532 nm and fluorescent light from the dye with a wavelength of 580 nm were captured by the CCD cameras (Flow Sense 4M), after being separated by a beam-splitter. The concentration of the dye was calculated assuming that the fluorescent intensity was proportional to the local dye concentration. Simultaneous PIV and PLIF measurements were taken at a sequence of streamwise distances in order to acquire the spatial concentration and velocity distributions at various downstream distances from the nozzle. In this experiment, the photographing rate was 4 Hz and 1000 consecutive distributions of velocity and concentration were captured simultaneously. The total duration of the sampling was thus 250 s, which was significantly longer than the largest time scales in the turbulent flow. In addition, the photographed area was approximately 4.75δ × 4.75δ with a spatial resolution of 0.04δ, which was enough to resolve fine-scale eddies in the turbulent flow. The mixing-length scale in the outer layer of wall turbulence was roughly estimated as 0.09δ [20] . For a reference, note also that the streamwise integral length scale obtained by integration of the streamwise two-point correlation coefficient was about 0.7δ.
3. Analysis Method
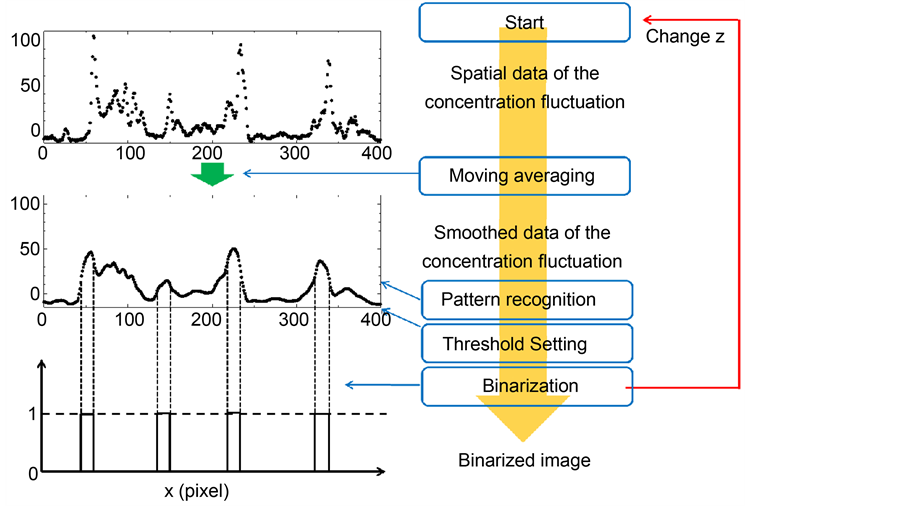
To calculate the scalar statistics of the high concentration spikes it is necessary to indicate the position and area of the spikes in the PLIF image describing the diffusing dye. In this study, a conditional sampling technique was used, which comprised the moving averaging, pattern recognition and binarizing by setting a threshold, as shown in Figure 4. Firstly, spatial data on concentration fluctuation C'(x, z) were obtained for different x at a fixed z from the raw PLIF images. Then C'(x, z) was smoothed by the moving averaging method [21] .
We assumed that the spikes were formed by the large-scale structure of turbulent eddies, and employed the smoothing window length NL (=LE/Δx) consisting of streamwise integral length scale LE and spatial resolution Δx of the photograph image. After that, by applying pattern recognition to the smoothed data, the corresponding waveform pattern was extracted. When the maximum value of concentration fluctuation in the waveform pattern recognized by the pattern recognition was higher than the threshold of concentration, the waveform pattern was extracted. In this technique, the threshold was the root mean square of C'(x, z). Thereafter, the concentration on the extracted waveform pattern was binarized as either zero or one: the concentration between the position of the largest gradient and the smallest gradient in the waveform pattern was binarized as one, while the other part was binarized as zero. When the above analysis was performed for all z on each PLIF image, the time series of the two-dimensional binarized images was obtained and the spikes were extracted. This spike extraction method is based on
Figure 4. Procedure of conditional sampling technique to extract high-concentration spikes.
both the concentration values and gradients, proposed in [16] by the authors. There are two notable points: that the conditional sampling technique doesn’t have any influence on the original image of the diffusing dye and that the versatility of the technique has a limit that the technique can be applied only when intended flow is homogeneous and steady.
4. Results and Discussion
4.1. Extraction of the High Concentration Spikes
The concentration of fluorescent dye was measured by the PLIF technique around four streamwise locations: x* = 5, 20, 40, and 60. Here, the superscript of * indicates normalization by the channel half width, i.e., x* = x/δ. For different streamwise locations, areas of the same size were selected based on the recorded PLIF images, and the further spike statistical analysis was done focused on the selected areas.
Figure 5 takes the original PLIF images for three locations for example. In Figure 5, higher brightness means higher fluorescent intensity, which is proportional to the local dye concentration. Figure 5 shows dye plumes with low and high concentration areas. Figure 6 shows the corresponding binarized images obtained by the conditional sampling technique mentioned above, and the length-scale mark is also shown in the figures. From Figure 5, it is found that the spanwise diffusion width of the plume spreads for downstream distance x*, which means that the diffusion of the plume progresses with
Figure 5. Images of diffusion and convection of dye emitted from nozzle obtained by PLIF measurement.
Figure 6. Binarized concentration images visualizing high concentration spikes obtained by the conditional sampling.
the diffusion time 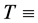 x/Uc. Here, the diffusion time of the plume is estimated using the downstream distance from the diffusion source and time-average streamwise velocity under Taylor’s frozen turbulence hypothesis. In the diffusing plume, the concentration fluctuates in space and there are areas having a high concentration and concentration gradient compared with the surroundings. Moreover, a meandering motion of the diffusing plume is not identified definitely in Figure 5, which was observed under the turbulent flow background at high Reynolds numbers [22] . The occurrence of the meandering motion depends on the relationship between the Lagrangian time scale of the turbulent field and the diffusion time of the plume, and can be observed when the diffusion time is shorter than the Lagrangian time scale. In this experiment, the Lagrangian time scale TL ≈ 0.036 s can be estimated by Equation (1), which was given by Hanna [23] .
x/Uc. Here, the diffusion time of the plume is estimated using the downstream distance from the diffusion source and time-average streamwise velocity under Taylor’s frozen turbulence hypothesis. In the diffusing plume, the concentration fluctuates in space and there are areas having a high concentration and concentration gradient compared with the surroundings. Moreover, a meandering motion of the diffusing plume is not identified definitely in Figure 5, which was observed under the turbulent flow background at high Reynolds numbers [22] . The occurrence of the meandering motion depends on the relationship between the Lagrangian time scale of the turbulent field and the diffusion time of the plume, and can be observed when the diffusion time is shorter than the Lagrangian time scale. In this experiment, the Lagrangian time scale TL ≈ 0.036 s can be estimated by Equation (1), which was given by Hanna [23] .
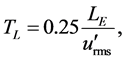 (1)
(1)
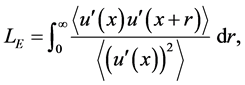 (2)
(2)
where LE denotes the Eulerian length scale in the streamwise direction, while u' (= u − Uc) denotes the streamwise velocity fluctuation, calculated from the streamwise instantaneous velocity u and the time-average streamwise velocity Uc. The Lagrangian time scale consists of the Eulerian length scale LE corresponding to the streamwise integral length scale and the streamwise turbulent intensity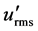 . The Lagragian time scale is smaller than the shortest diffusion time T = 0.05 s among the measurement positions. Based on Taylor’s diffusion theory, in this experiment, a large part of the diffusion of the plume in the photographed areas corresponded to long-time diffusion.
. The Lagragian time scale is smaller than the shortest diffusion time T = 0.05 s among the measurement positions. Based on Taylor’s diffusion theory, in this experiment, a large part of the diffusion of the plume in the photographed areas corresponded to long-time diffusion.
The white areas in Figure 6 stand for the high concentration spikes, while the black areas indicate zero or low concentration areas. Therefore, Figure 6 shows the existence of the high concentration spikes in the diffusing plume. Note here that Figure 6 of the binarized images are obtained from Figure 5 of the original raw PLIF images by applying the above-mentioned sampling technique. Comparing the corresponding original and binarized images, it can be seen that high concentration spikes are distinguished with clear outlines by extraction. Moreover, the high concentration spikes are scattered randomly in Figure 6. From Figure 5 and Figure 6, it can be seen that a large number of high concentration spikes exist even at the edge of the plume where the concentration is very low.
The reason is that such a low-concentration edge area has a large concentration gradient, so the spikes can be recognized. Actually, through extraction by the conditional sampling technique, the low-concentration edge area of the plume is also taken seriously, which is more reasonable than analyzing only based on the plume concentration. As x* increases, the white areas appear clearer and their number increases in the image. Considering that the high concentration spikes are formed by the organized structure of turbulence and extracted by judging the plume concentration by concentration values as well as concentration gradients, it can be suspected that the behavior of the spikes follows a totally different diffusion law from that of the plume.
4.2. Diffusion Width
According to Taylor’s diffusion theory, the spanwise diffusion width of the diffusing plume has a strong relationship with the diffusion theory. This section investigates the spanwise diffusion width of the high concentration spikes. The spanwise diffusion width of the high concentration spikes can be defined as the standard deviation calculated from the spanwise distribution of the existence probability of the spikes. The existence probability of the spikes is calculated by
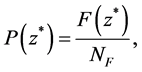 (3)
(3)
where F(z*) stands for the number of high concentration spikes for a fixed z* in the selected area for statistical analysis, while NF is the number of all the spikes in the same area. The selected area for statistical analysis is the same length as the domain in Figure 5 and Figure 6 in the spanwise direction, while in the streamwise direction, the length of domain ΔH ( Ub × Δt) equals the bulk mean velocity multiplied by time step of the PLIF images. Moreover, the statistical area is at the center of the domain shown in Figure 5 and Figure 6 in the streamwise direction. The number of all the spikes in the selected area is calculated using a labeling technique [16] . The existence probability in this study means the ratio of the spikes along z* to the total number of spikes in the statistical area.
Ub × Δt) equals the bulk mean velocity multiplied by time step of the PLIF images. Moreover, the statistical area is at the center of the domain shown in Figure 5 and Figure 6 in the streamwise direction. The number of all the spikes in the selected area is calculated using a labeling technique [16] . The existence probability in this study means the ratio of the spikes along z* to the total number of spikes in the statistical area.
Figure 7 shows the spanwise existence probability distributions of the spikes at three downstream distances. The solid lines in the figure are the fitted Gaussian distribution curves for the calculated existence probability. Although there is some discrepancy between the calculated distributions and the fitting curves, we can still say that the spanwise distribution of the existence probability almost follows the Gaussian shape. Basically, a statistical random process of an event follows the Gaussian distribution. Therefore, the transport process of the high concentration spikes is a kind of random process similar to that of the plume.
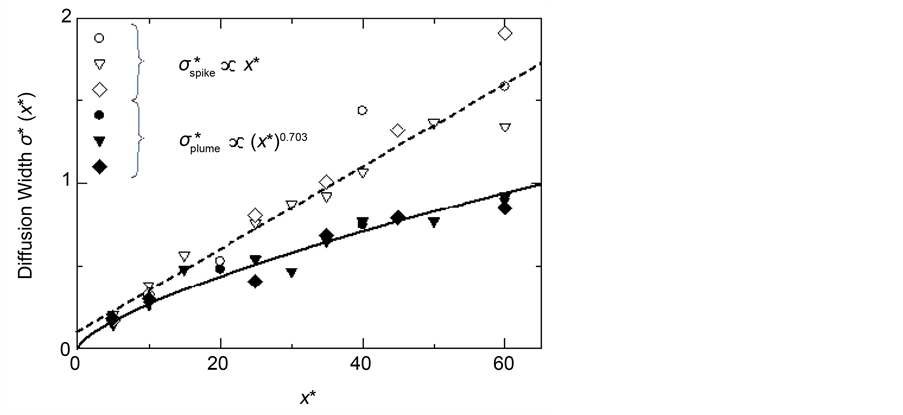
The variations of the standard deviation 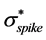 of the probability of spikes as a function of the downstream distance are shown in Figure 8. While, for comparison, the diffusion width of the concentration plume
of the probability of spikes as a function of the downstream distance are shown in Figure 8. While, for comparison, the diffusion width of the concentration plume 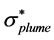 defined as the standard deviation of the spanwise mean concentration distribution of the plume is also calculated and shown in the figure. The PLIF images obtained by measurements repeated three times are used. This is done to enhance the reliability by having more data dots in the figure. The dashed line in Figure 8 is the approximate straight line to the standard deviations of the spikes by the least square method, while the solid line is the approximated curve to the standard deviations of the plume. It can be seen that the diffusion width of the concentration plume increases as a power function of the downstream distance, corresponding to the result of Webster et al. [24] . Meanwhile, the diffusion width of the high concentration spikes increases almost linearly with downstream distance, and the increase rate is larger than that of the plume width. Moreover, the diffusion widths of the spikes are larger than the corresponding plume widths. The reason is that the high concentration
defined as the standard deviation of the spanwise mean concentration distribution of the plume is also calculated and shown in the figure. The PLIF images obtained by measurements repeated three times are used. This is done to enhance the reliability by having more data dots in the figure. The dashed line in Figure 8 is the approximate straight line to the standard deviations of the spikes by the least square method, while the solid line is the approximated curve to the standard deviations of the plume. It can be seen that the diffusion width of the concentration plume increases as a power function of the downstream distance, corresponding to the result of Webster et al. [24] . Meanwhile, the diffusion width of the high concentration spikes increases almost linearly with downstream distance, and the increase rate is larger than that of the plume width. Moreover, the diffusion widths of the spikes are larger than the corresponding plume widths. The reason is that the high concentration
Figure 7. Spanwise existence probability distributions of high concentration spikes at downstream distances of x* = 5, 40, and 60.
Figure 8. Diffusion widths of high concentration spikes and plume versus downstream distance x*.
spikes are also extracted at the edge of the plume where there are low-concentration and large concentration gradients with the surrounding areas. To further clarify the difference between high concentration spikes and plume, the length scale, the ratio of mean concentration, and the turbulent diffusion coefficient were calculated, and the diffusion process of the spike is discussed.
4.3. Length Scale
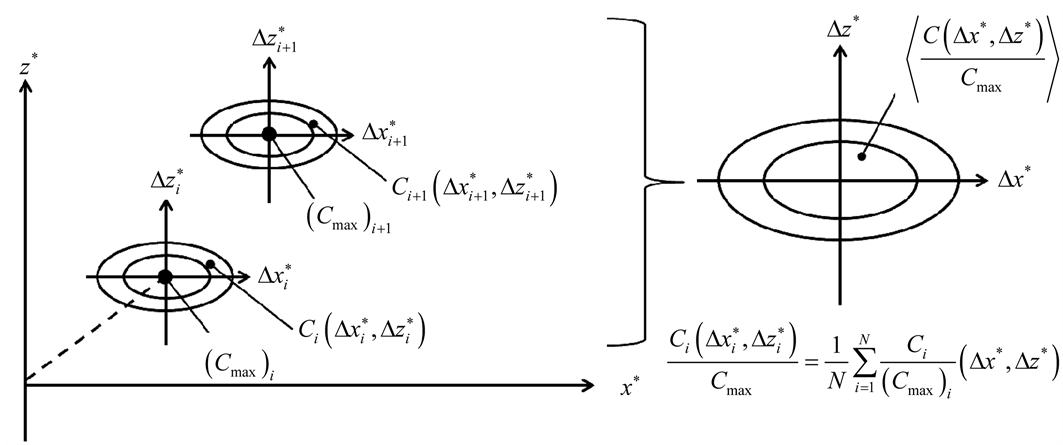
From Figure 6, it is difficult to understand the relationship between the concentration spikes and the increasing downstream distances. To provide quantitatively analysis of the relationship, the length scale of the high concentration spikes was calculated, in which the mean concentration of the spikes was involved. Figure 9 is a schematic diagram showing how to obtain the mean concentration distribution of spikes. Firstly, each high concentration spike on a binarized image was distinguished through a labeling technique and numbered in sequence as
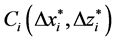
Figure 9. Calculation of mean concentration distribution in high concentration spikes.
Figure 10. Mean concentration distribution around high concentration spikes at downstream distance of x* = 20 obtained by conditional average method.
the high concentration spikes can be imagined to be departing from this center. Moreover, the mean concentration distribution around the high concentration spikes takes the form of an ellipse. The streamwise breadth of the distribution, based on the line of Δz* = 0, is larger than the spanwise breadth on the line of Δx* = 0. The concentration field in this experiment has a larger spanwise concentration gradient than that in the streamwise direction, which has great influences on the anisotropy of the distribution breadths in spanwise and streamwise direction. Focusing on Δx* = 0 extracts the spanwise mean concentration distribution through the resultant spike center, which combined with the results from other streamwise locations, is shown in Figure 11.
It is obvious that the profiles of the four streamwise locations coincide and the spanwise average length scale of the high concentration spike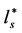


Figure 11. Mean concentration distributions in spanwise direction around the center of the high concentration spikes at several downstream distance obtained by the conditional average method.
centroid, and the concentration in the meandering plume hardly changed. By analogy, the relative scale of the turbulent eddies with respect to the length scale, calculated from the average concentration distribution of the spike, determines the diffusion process of the spike. For l* larger than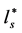
4.4. Mean Concentration Ratio
The above section shows that the diffusivity of the inner concentration allows us to discuss the diffusion process. This section calculates the mean concentration ratio of the spikes to the plume, and investigates the diffusivity of the concentration inside the spikes. The mean concentration and the ratio of mean concentration are respectively defined by Equation (4) and Equation (5).
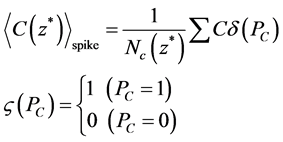
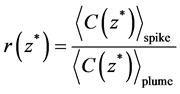
where, Nc denotes the total number of recognized spikes for a fixed z*; PC is binarized data indicating the existence of the high concentration spikes; ζ is an indicator function. Figure 12 gives the spanwise mean concentration distribution of the spikes and the
Figure 12. Mean concentration distributions of high concentration spikes and plume at downstream distance of x* = 20.
plume at x* = 20 for example. The mean concentration distributions are normalized by the maximum concentration in the spikes. As can be seen from Figure 12, the spanwise distribution shape of mean concentration for the spikes and plume are similar, both approximately following the Gaussian distribution. Considering that the spanwise mean concentration distribution matches Gaussian distribution when the mass is distributed as random walk [26] , it is inferred that the concentration distribution in the high concentration spikes is based on random walk.
Figure 13 shows the mean concentration ratio at each measurement position. This figure plots the ratios only for one spanwise side because the mean concentration ratio distributions are line-symmetric with respect to z* = 0. Comparing the two distributions, the mean concentration ratio and the mean concentration of the plume, it seems that the ratio distribution continues increasing to the area where the mean concentration of the plume is approximately zero. Inevitably, the mean concentration ratio exceeds one because the mean concentration of the high concentration spikes extracted as the areas with high concentration in the plume is larger than that of the plume. In addition, the ratio should be constant with spanwise distance when the declines of concentration in the plume and the spike are the same, as is the case when they move the same distance in the spanwise direction due to diffusion phenomena. The result shows that the mean concentration ratio increases with spanwise distance, which means that the decline rate of concentration in the plume is larger than that in the high concentration spike with the same distance in spanwise direction. Therefore, the high concentration spike moves to the spanwise direction with low diffusivity of the internal concentration compared to the concentration plume, and the gap in diffusivity continues increasing to the edge of the concentration plume.
Figure 13. Mean concentration ratio of high concentration spikes to plume at downstream distances of x* = 5, 20, 40, 60.
4.5. Apparent Diffusion Coefficient
We consider that there are two types of diffusivity of concentration in turbulent mass diffusion: one is the internal diffusivity of internal concentration with the travel distance, and the other is the external diffusivity relating to the transport of the concentration in a turbulent flow. To discuss the external diffusivity, the apparent diffusion coefficient is calculated in this section. The apparent diffusion coefficient can be understood as the magnitude of concentration flux divided by the local mean concentration gradient. Apparent diffusion coefficients in spanwise direction for plume and spikes are respectively calculated by Equation (6) and Equation (7) as follows,


where w' (=w − W>) denotes the spanwise velocity fluctuation, calculated from spanwise instantaneous velocity w and time-average spanwise velocity
Figure 14. Apparent diffusion coefficients of high concentration spikes and plume at downstream distances of x* = 5, 20, 40, and 60.
As is indicated, the apparent diffusion coefficient of the plume (Kz)plume is constant, independent of both the streamwise and spanwise distances, which implies that the assumption of homogeneous turbulent flow in our experiment is reasonable. However, unlike the coefficient of plume, (Kz)spike increases linearly with spanwise distance. Our analysis shows that the concentration flux driven by spanwise concentration gradient in the spike is more and more dominant as spanwise distance increases, compared with the concentration flux driven by spanwise concentration gradient in the plume. Also, there is a strong correlation between the spanwise velocity fluctuation and the concentration fluctuation. Actually, in a homogeneous turbulent flow, the high concentration fluctuation has a large velocity fluctuation and the relationship between the concentration and velocity fluctuations is linear, as was reported by [27] [28] . From the mean concentration ratio, it is found that there is a gap between the mean concentrations of the spikes and plume, which means that the average concentration fluctuation of the spikes based on the mean concentration of the plume increases with the spanwise distance. Based on the linear relationship between the concentration fluctuation and velocity fluctuation, the average velocity fluctuation of the spikes increases with the spanwise distance. This increase leads to an increase of the apparent diffusion coefficient of the spikes. Moreover, comparison of the linear approximations at different streamwise distances reveals a decreasing slope of the fitted line towards an increasing streamwise distance. The cause of this is considered to be that the concentration fluctuation is reduced as the concentration approaches spatial homogeneity and thus the concentration flux decreases. Consequently, it can be seen that the diffusion process of the spikes differs from that of the plume.
4.6. The Diffusion Theory of the High Concentration Spikes
Combining the results shown above, we discuss the diffusion process of a high concentration spike and its difference from the plume. According to Taylor [4] , the diffusion of the concentration plume can be distinguished into meandering diffusion and relative diffusion. The meandering diffusion represents the movement of the mass center of the concentration plume, while the relative diffusion represents the spreads of the plume width departing from the mass center. When the diffusion time T is shorter than the time integral scale TL of the turbulent field (T < TL), meandering diffusion is predominant over relative diffusion and the diffusion width spreads in proportion to T. On the other hand, when T > TL, relative diffusion dominates and the diffusion width is proportional to the square root of T. In addition to Taylor’s diffusion theory, as said before, Yee and Wilson [25] described the action of eddies of length scale l on the plume in accordance with the relative sizes of l with respect to the length scale of the average instantaneous concentration distribution of the diffusing plume σr. When l > σr, eddies of this size result in the meandering motions of the instantaneous plume centroid. Eddy scales with l < σr act to break up the plume to initiate a turbulent cascade of concentration variance (energy) from the large-scale motions onto the smaller-scale motions. Moreover, they reported that the length scale σr and the inner concentration of the instantaneous plume in meandering motions hardly change with the travel distance of the plume, and an increase of the length scale σr is caused when l ≈ σr. Therefore, there are four factors related to the diffusion process of the concentration plume diffusing in a turbulent flow: diffusion time, diffusion width, length scale, and the diffusivity of the internal concentration of the plume.
We cannot confirm the meandering motions of the diffusing plume in Figure 5, and suppose that a large part of the diffusion of the plume is strongly dominated by relative diffusion, based on the relationship between the diffusion time of the plume and the time integral scale of the turbulent flow. On the other hand, the calculated scalar statistics of the high concentration spikes have the same properties of meandering diffusion. The diffusion width of the high concentration spikes increases linearly with the downstream distance as is shown in Figure 8. Figure 11 shows that the average length scale of the high concentration spikes keeps constant for downstream distance and is smaller than the length scale of the eddies. In addition, from the result of Figure 13, it is confirmed that the high concentration spike has a lower apparent diffusivity of inner concentration while moving in turbulent flow, compared with that of a plume dominated by relative diffusion. Consequently, it is concluded that the diffusion of a high concentration spike is dominated by meandering diffusion regardless of the diffusion process of the plume. The aggregation diffusion of the spikes is considered to be reflected in the combination of a high concentration spike dominated by a meandering diffusion. This may be the reason why diffusion width increases linearly for the downstream distance. Moreover, the number of spikes per unit of area increases with increasing downstream distance, as shown in Figure 6. Accordingly, neither the number nor the inner concentration of the high concentration spikes extracted from the concentration plume follows the conservation law which the plume diffusion satisfies, and this is the major difference between the spike and the plume.
To reduce the damage from pollutant diffusion it is important to predict the diffusion of not only the mean concentration but also the concentration fluctuation. It is concluded that the large concentration fluctuation occurring at any position in a turbulent flow is greatly affected by meandering diffusion. This knowledge is expected to enhance the accuracy of diffusion prediction of concentration fluctuation.
5. Conclusions
This paper focuses on the high concentration spike formed by turbulent structures, and we investigate their diffusion process from the viewpoint of the difference with the concentration plume.
In the mass diffusion on a quasi-homogenous turbulence background, the concentration and velocity distributions were obtained by PLIF and PIV measurements. The conditional sampling technique was applied for extracting spikes from plumes captured in concentration images. By calculating the spanwise existence probability of the spikes, we found that the existence probability follows the Gaussian distribution and its standard deviation increases linearly with downstream distance from the emission source. As regards the average length scale of the spikes, it is found to be constant for the downstream distance and smaller than the integral scale of eddies, which differs from the character of the concentration plume. The turbulent diffusion coefficient of the spikes is proportional to the spanwise distance, while that of the plume is constant.
From all the results, we conclude that the diffusion process of a high concentration spike is dominated by the meandering diffusion consistently in a turbulent flow and differs from that of the plume. This knowledge is expected to help with the accurate diffusion prediction of concentration fluctuation.
Cite this paper
Endo, M., Shao, Q.Q., Tsukahara, T. and Kawaguchi, Y. (2016) Diffusion Process of High Concentration Spikes in a Quasi-Homogeneous Tur- bulent Flow. Open Journal of Fluid Dynamics, 6, 371-390. http://dx.doi.org/10.4236/ojfd.2016.64028
References
- 1. Takemura, T., et al. (2011) A Numerical Simulation of Global Transport of Atmospheric Particles Emitted from the Fukushima Daiichi Nuclear Power Plant. SOLA, 7, 101-104.
http://www.jstage.jst.go.jp/browse/sola
https://doi.org/10.2151/sola.2011-026 - 2. Terada, H. and Chino, M. (2008) Development of an Atmospheric Dispersion Model for Accidental Discharge of Radionuclides with the Function of Simultaneous Prediction for Multiple Domains and Its Evaluation by Application to the Chernobyl Nuclear Accident. Journal of Nuclear Science and Technology, 45, 920-931. https://doi.org/10.1080/18811248.2008.9711493
- 3. Chino, M., Nakamura, H., Nagai, H., Terada, H., Katata, G. and Yamazawa, H. (2011) Preliminary Estimation of Release Amounts of 131I and 137Cs Accidentally Discharged from the Fulushima Daiichi Nuclear Power Plant into the Atmosphere. Journal of Nuclear Science and Technology, 48, 1129-1134. https://doi.org/10.1080/18811248.2011.9711799
- 4. Taylor, G.I. (1921) Diffusion by Continuous Movement. Proceedings of the Royal Society A, 20, 196-211.
- 5. Richardson, L.F. (1926) Atmospheric Diffusion Shown on a Distance-Neighbor Graph. Proceedings of the Royal Society A, 110, 709-737. https://doi.org/10.1098/rspa.1926.0043
- 6. Brown, R.J. and Bilger, R.W. (1996) An Experiment Study of a Reactive Plume in Grid Turbulence. Journal of Fluid Mechanics, 312, 373-407.
https://doi.org/10.1017/S0022112096002054 - 7. Lemoine, F., Wolff, M. and Lebouche, M. (1997) Experimental Investigation of Mass Transfer in a Grid-Generated Turbulent Flow Using Combined Optical Methods. International Journal of Heat and Mass Transfer, 40, 3255-3266. https://doi.org/10.1016/S0017-9310(96)00385-7
- 8. Lemoine, F., Antoine, Y. and Lebouche, M. (2000) Some Experimental Investigations on the Concentration Variance and Its Dissipation Rate in a Grid Generated Turbulent Flow. International Journal of Heat and Mass Transfer, 43, 1187-1199.
https://doi.org/10.1016/S0017-9310(99)00204-5 - 9. Nagata, K., Suzuki, H., Sakai, Y., Hayase, T. and Kubo, T. (2008) Direct Numerical Simulation of Turbulent Mixing in Grid-Generated Turbulence. Physica Scripta, 132, 1-5.
- 10. Antonia, R.A., Chambers, A.J., Britz, D. and Browne, L.W.B. (1986) Organized Structure in a Turbulent Plane Jet: Topology and Contribution to Momentum and Heat Transport. Journal of Fluid Mechanics, 172, 211-229. https://doi.org/10.1017/S0022112086001714
- 11. Buch, K.A. and Dahm, W.J.A. (1996) Experimental Study of the Fine-Scale Structure of Conserved Scalar Mixing in Turbulent Shear Flows. Journal of Fluid Mechanics, 317, 21-71.
https://doi.org/10.1017/S0022112096000651 - 12. Tong, C. and Warhaft, Z. (1994) On Passive Scalar Derivative Statistics in Grid Turbulence. Physics of Fluids, 6, 2165-2176. https://doi.org/10.1063/1.868219
- 13. Holzer, M. and Siggia, E.D. (1994) Turbulent Mixing of a Passive Scalar. Physics of Fluids, 6, 1820-1837. https://doi.org/10.1063/1.868243
- 14. Webster, D.R., Volyanskyy, K.Y. and Weissburg, M.J. (2011) Sensory-Mediated Tracking Behavior in Turbulent Chemical Plumes. Proceedings of the 7th International Symposium on TSFP, Ottawa, 28-31 July 2011, 1-6.
- 15. Page, J.L., Dickman, B.D., Webster, D.R. and Weissburg, M.J. (2011) Getting Ahead: Context-Dependent Responses to Odorant Filaments Drive Along-Stream Progress during Odor Tracking in Blue Crabs. Journal of Experimental Biology, 214, 1498-1512.
https://doi.org/10.1242/jeb.049312 - 16. Endo, M., Tsukahara, T. and Yasuo, K. (2015) Relationship between Diffusing-Material Lumps and Organized Structures in Turbulent Flow. Proceedings of the 5th International AJK Joint Fluids Engineering Conference, Seoul, 26-31 July 2015, 1747-1753.
- 17. Hu, H., Saga, T., Kobayashi, T. and Taniguchi, N. (2002) Simultaneous Velocity and Concentration Measurements of a Turbulent Jet Mixing Flow. Annals of the New York Academy of Sciences, 972, 254-259. https://doi.org/10.1111/j.1749-6632.2002.tb04581.x
- 18. Diez, F.J., Bernal, L.P. and Faeth, G.M. (2005) PLIF and PIV Measurements of the Self-Preserving Structure of Steady Round Buoyant Turbulent Plumes in Crossflow. International Journal of Heat and Fluid Flow, 26, 873-882.
https://doi.org/10.1016/j.ijheatfluidflow.2005.10.003 - 19. Janzen, J.G., Herlina, H., Jirka, G.H., Schulz, H.E. and Gulliver, J.S. (2010) Estimation of Mass Transfer Velocity Based on Measured Turbulence Parameters. AIChE, 56, 2005-2017.
- 20. Pope, S.B. (2000) Turbulent Flows. Cambridge University Press, Cambridge, 305-308.
- 21. Cryer, J.D. (1983) Time Series Analysis. Duxbury Press, Boston, 1-487.
- 22. Kosugi, K., Makita, H. and Haniu, H. (2014) Experiment Investigation on Turbulent Diffusion Phenomena of Meandering Plume in the Quasi-Isotropic Turbulent Field (Variation of Mean Concentration Properties for Turbulent Reynolds Numbers). Transactions of the JSME, 80, 1-14. (In Japanese)
- 23. Hanna, S.R. (1981) Turbulent Energy and Lagrangian Time Scales in the Planetary Boundary Layer. Proceedings of the 5th Symposium on Turbulence, Diffusion, and Air Pollution, Atlanta, 9-13 March 1981, 61-62.
- 24. Webster, D.R., Rahman, S. and Dasi, L.P. (2003) Laser-Induced Fluorescence Measurements of a Turbulent Plume. Journal of Engineering Mechanics, 129, 1130-1137.
https://doi.org/10.1061/(ASCE)0733-9399(2003)129:10(1130) - 25. Yee, E. and Wilson, D.J. (2000) A Comparison of the Detailed Structure in Dispersing Tracer Plumes Measured in Grid-Generated Turbulence with a Meandering Plume Model Incorporating Internal Fluctuations. Boundary-Layer Meteorology, 94, 253-296.
https://doi.org/10.1023/A:1002457317568 - 26. Metzler, R. and Klafter, J. (2000) The Random Walk’s Guide to Anomalous Diffusion: A Fractional Dynamics Approach. Physics Reports, 339, 1-77.
https://doi.org/10.1016/S0370-1573(00)00070-3 - 27. Pope, S.B. (1985) PDF Methods for Turbulent Reactive Flows. Progress in Energy and Combustion Science, 11, 119-192. https://doi.org/10.1016/0360-1285(85)90002-4
- 28. Brethouwer, G. and Nieuwstadt, F.T.M. (2001) DNS of Mixing and Reaction of Two Species in a Turbulent Channel Flow: A Validation of the Conditional Moment Closure. Flow, Turbulence and Combustion, 66, 209-239. https://doi.org/10.1023/A:1012217219924