Open Journal of Fluid Dynamics
Vol.05 No.04(2015), Article ID:62459,11 pages
10.4236/ojfd.2015.54037
Non-Darcy Mixed Convection between Differentially Heated Vertical Walls Filled with a Porous Material: Application of New Modified Adomian Decomposition Method
A. K. Tiwari, Premlata Singh
Department of Applied Mathematics, Birla Institute of Technology, Mesra, Ranchi Extension Centre, Patna, India
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 November 2015; accepted 25 December 2015; published 30 December 2015
ABSTRACT
This paper presents non-Darcy mixed convective flow of an incompressible and viscous fluid in a differentially heated vertical channel filled with a porous material in the presence of a temperature dependent source/sink. The analytical solution of fourth order non-linear ordinary differential equation for temperature field, which is formed by eliminating velocity field from system of governing equations in non-dimensional form, is obtained by using new modified Adomian decomposition method (NMADM) in terms of various parameters. In order to illustrate the interactive influences of governing parameters on the temperature and velocity fields, a numerical study of the analytical solution is performed with respect to three categories of transport processes i) when forced convection is dominated, ii) when forced and natural convection are equal and iii) when natural convection is dominated. Analysis of all categories has revealed that the temperature and velocity profiles are increasing function of modified Darcy number while decreasing function of Forchheimer number.
Keywords:
Non-Darcy Mixed Convection, Porous Media, Differentially Heated, New Modified Adomian Decomposition Method (NMADM)

1. Introduction
Non-Darcy mixed convective flow and heat transfer between two vertical walls and annuli filled with porous materials have been extensively studied in the past and attracted attention of research workers due to its many engineering applications. Some of their related applications are, for example, geothermal energy extraction, nuclear waste disposal, thermal insulation, solid matrix heat exchanger, thermal energy storage in underground aquifers, etc. The analytic solutions corresponding to different physical situations in a vertical channel are presented by several authors [1] -[7] .
The numerical calculation of the fully developed mixed convection in a heated vertical channel filled with a porous medium and imposed uniflux at the plates is performed by Chen et al. [8] using the Brinkman Forchheimer-extended Darcy model. In this paper, both the buoyancy assisted and buoyancy opposed flows are considered. Murlidhar [9] studied mixed convective flow and heat transfer in the annular region between concentric cylinders filled with fluid-saturated porous material by using the Darcy model. Hadim and Chen [10] showed the Darcy number effects on the buoyancy-assisted mixed convection in the entrance region of a vertical channel with asymmetric heating for fixed values of Reynolds number, Forchheimer number, Prandtl number and modified Darcy number. The study performed by Vafai and Kim [11] in case of forced convection in a porous medium bounded by two parallel plates has shown that for a high-permeability porous medium the thickness of the momentum boundary layer depends on both the Darcy number and the inertia parameter while that for a low- permeability porous medium depends only on the Darcy number. Nadeem and Akbar [12] presented an exact solution for the temperature field, while the velocity field of the model was solved by Adomian decomposition method. Neild et al. [13] have analyzed theoretically fully developed forced convection in a fluid saturated porous medium channel bounded by parallel plates by obtaining general solution which has no restrictions and exists for all values of the Darcy number and Forchheimer inertia coefficient as well as also for a porous medium having effective viscosity different from the fluid viscosity. A regular perturbation technique has been employed by Beckett [14] to further investigate the nature of the known equations governing fully developed forced and free convective flow between heated verticals walls. The work of Chamkha [15] is focused on the laminar fully developed mixed convection flow of an electrically conducting fluid in a vertical channel in the presence of a magnetic field and heat generation or absorption effects. In this study various analytical solutions for the velocity and temperature fields were obtained for different special cases of heating and cooling of the wall. Recently, Khan et al. [16] have given the exact solutions for the unsteady flow induced by the time-dependent motion of a plane wall between two side walls perpendicular to the plane through porous medium by means of Fourier sine transform.
The main purpose of the present paper is to examine non-Darcy mixed convection in a differentially heated vertical channel filled with a porous material in the presence of temperature dependent source/sink. The analytical solution of the temperature field has been obtained using new modified Adomian decomposition method given by Wazwaz and El-Sayed [17] in terms of the physical parameters appearing in the governing equations. Finally, results are presented by graphs corresponding to the temperature and velocity fields for different values of the governing parameters.
2. New Modified Adomian Decomposition Method
In order to illustrate the basic idea of this method, let us consider an ordinary differential equation taken by Wazwaz [18] as follows:
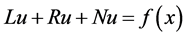 , (1)
, (1)
with prescribed boundary conditions. Here u is unknown function, L is an easily invertible linear operator having highest order derivative and R is a linear differential operator of order less than L. Nu represents the non-linear terms and f is the source terms. Applying the inverse operator 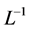 in both sides of Equation (1) and using the given boundary conditions, we have
in both sides of Equation (1) and using the given boundary conditions, we have
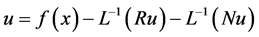 . (2)
. (2)
Differences among different Adomian decomposition methods can be distinguish on the basis of dividing the source term  into components. When
into components. When 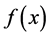 is divided into
is divided into
i) one component then it is known as ADM,
ii) two components then it is known as MADM,
iii) n components then it is known as NMADM, where n is the degree of .
.
According to NMADM, we therefore express 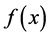 in the form
in the form
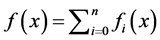 . (3)
. (3)
The standard Adomian method defines the solution of u(x) by the series
 , (4)
, (4)
where the components 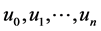 are usually determined recursively using the new relationship expressed in the form
are usually determined recursively using the new relationship expressed in the form
 (5)
(5)
3. Mathematical Analysis
Consider the non-Darcy mixed convective flow of a viscous incompressible fluid between two vertical plane walls separated by a distance 2H and filled with a porous material in the presence of a temperature dependent source/sink and under a constant pressure gradient. We employ here a Cartesian coordinate system with origin at the central line of the channel having 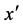 -axis along the vertical direction and
-axis along the vertical direction and  -axis perpendicular to the walls. For fully developed laminar flow, the velocity has only a vertical component and is a function of
-axis perpendicular to the walls. For fully developed laminar flow, the velocity has only a vertical component and is a function of 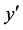 only. The equation of continuity is being identically satisfied. All the physical properties are assumed to be constant except the density variation in the buoyancy term which is satisfied by the Boussinesq’s approximation. If we define the dimensionless quantities as
only. The equation of continuity is being identically satisfied. All the physical properties are assumed to be constant except the density variation in the buoyancy term which is satisfied by the Boussinesq’s approximation. If we define the dimensionless quantities as
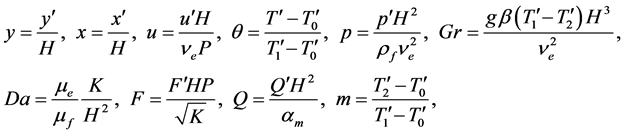 (6)
(6)
the governing equations of the model such as conservation of momentum and thermal energy in non-dimensional form are obtained as follows (Chen et al. [7] ):


The first term in the R.H.S. of Equation (7) is the Brinkman term, the second is the Darcy and the third is the Forchheimer term, hence the momentum transfer in the porous region is based on the Brinkman-Forchheimer-ex- tended Darcy model. The boundary conditions of the problem in non-dimensional form are obtained as

All the symbols used in the above equations are defined in the nomenclature.
Now, putting the value of u from Equation (8) into the Equation (7), we get a fourth order non-linear ordinary differential equation in of the form:

where

For the solution of Equation (10), we use new modified Adomian decomposition method, proposed by Wazwaz and El-Sayed [17] and for this purpose Equation (10) in operator form can be written as follows:

Applying the inverse operator 

where 
Now, we can decompose θ as

and according to Equation (12) source function 

As suggested by Wazwaz and El-Sayed [17] , we get





According to Equation (13), the expression for temperature field can be written as

The symbols used in the above expressions as a constant are given in appendix. After obtaining the solution for temperature field in the form in Equation (16), we have derived the solution for velocity field by using Equation (8) but not presented here for the sake of brevity.
4. Skin Friction and Nusselt Number at the Walls
In order to measure the shear stress and the heat transfer rate at the boundaries, the expressions for the skin friction in non-dimensional form and Nusselt number on the channel walls have been obtained by using the following relations respectively:


But they are not given here for the sake of brevity.
5. Results and Discussions
We investigate the interactive effects of the dimensionless parameters such as modified Darcy number Da, Forchheimer number F, source/sink parameter Q and wall temperature ratio m, on heat and fluid flow between two vertical walls having differentially heating corresponding to the following categories of flow formation:
i) when forced convection is dominated (
ii) when both convections are equal (
iii) when natural convection is dominated (
In the presence of source

In all three cases, we observed that the temperature and velocity profiles are increasing function of modified Darcy number while decreasing function of Forchheimer number. The effect of Darcy number is more visible in the case of natural convective dominated flow. The fluid velocity near the wall region slowly increases with the increase of Da, but it is more significant in the region near to the walls when flow is dominated by natural convection.
We have plottedin the Figure 4(a) and Figure 4(b) the temperature and velocity profiles in the presence of sink 

Figures 5(a)-7(a), Figures 5(b)-7(b) illustrate the effects of wall temperature ratio (m) on temperature and velocity profiles corresponding to cases three types of categories. From these figures in the presence of source
Figure 1. Effects of the modified Darcy number Da and Forchheimer number F on the temperature and the velocity profiles by 1(a) and 1(b) respectively in the presence of source for when forced convection is dominated and here Q = 5.0, m = 1.0.
Figure 2. Effects of the modified Darcy number Da and Forchheimer number F on the temperature and the velocity profiles by 2(a) and 2(b) respectively in the presence of source for when both convections are equal and here Q = 5.0, m = 1.0.
Figure 3. Effects of the modified Darcy number Da and Forchheimer number F on the temperature and the velocity profiles by 3(a) and 3(b) respectively in the presence of source parameter for when natural convection is dominated and here Q = 5.0, m = 1.0.
Figure 4. Effects of the modified Darcy number Da and Forchheimer number F on the temperature and the velocity profiles by 4(a) and 4(b) respectively in the presence of sink for when forced convection is dominated and here Q = −5.0, m = 1.0.
Figure 5. Effects of the modified Darcy number Da and Forchheimer number F on the velocity profiles by 5(b) in the presence of sink for when both convections are equal and here Q = −5.0, m = 1.0.
Figure 6. Effects of the wall temperature ratio m and source/sink parameter Q on the temperature and the velocity profiles profiles by 6(a) and 6(b) respectively for when forced convection is dominated and here Da = 0.01, F = 0.2.
Figure 7. Effects of the wall temperature ratio m and source/sink parameter Q on the temperature and the velocity profiles profiles by 7(a) and 7(b) respectively for when both convections are equal and here Da = 0.01, F = 0.2.
Figure 8. Effects of the wall temperature ratio m and source/sink parameter Q on the temperature and the velocity profiles profiles by 8(a) and 8(b) respectively for when natural convection is dominated and here Da = 0.01, F = 0.2.
parameter, it shows that when m increases, the flow near wall 1 is more and more accelerated and flow reversal is observed in the vicinity of wall 2. Meanwhile wall 1 becomes increasingly hotter relatively to wall 2 and the temperature profiles approaches a linear distribution. In the presence of sink parameter, the temperature profile slopes on both walls remain constant in accordance with the differentially heating conditions. As 
A close study of the Table 1 and Table 2 for different values of modified Darcy number Da, Forchheimer number F, wall temperature ratio m and source/sink parameter Q presents the dependence of skin friction and Nusselt number corresponding to three categories at the walls 


Table 1. Numerical values of dimensionless Skin-friction at channel walls.
Table 2. Numerical values of dimensionless Nusselt number at channel walls.
However, the Nusselt number at the right wall (y = 1) in each category positive, which indicates physically that heat flows from the walls into the porous region. We observed that Nusselt number for each category decreases with wall temperature ratio m and increases with Forchheimer number F. On comparing the Nusselt number for each category of the wall at y = 1.0 and y = −1.0, it is observed that it increases with Da when 

6. Conclusion
New modified Adomian decomposition method has been used to find the analytical solution of the governing equations describing the non-Darcy mixed convective flow of an incompressible and viscous fluid in a differentially heated vertical channel filled with a porous material in the presence of a temperature dependent source/ sink. The effect of all physical parameters appearing in the governing equations is more visible when natural convection is dominated in comparison with fully forced convection in the presence of source parameter. The impact of all categories is more effective in the presence of source than sink. Also, it has been observed that the numerical values of all skin friction components increase with the increase of wall temperature ratio (m) and Forchheimer number (F). Increasing value of Gr from P i.e. forced convection to natural convection induces flow acceleration near both walls and consequently flow deceleration in the central line of the channel. Eventually this tendency can lead to flow reversal at the centerline but the corresponding value of Gr either greater, equal or less than P is of questionable physical signification (see discussion by Barletta and Zanchini [19] on stability).
Cite this paper
A. K.Tiwari,PremlataSingh, (2015) Non-Darcy Mixed Convection between Differentially Heated Vertical Walls Filled with a Porous Material: Application of New Modified Adomian Decomposition Method. Open Journal of Fluid Dynamics,05,380-390. doi: 10.4236/ojfd.2015.54037
References
- 1. Szeri, A.Z. and Rajagopal, K.R. (1985) Flow of a Non-Newtonian Fluid between Heated Parallel Plates. International Journal of Non-Linear Mechanics, 20, 91-101.
http://dx.doi.org/10.1016/0020-7462(85)90003-4 - 2. Aung, W. and Worku, G. (1986) Theory of Fully Developed Combined Convection Including Flow Reversal. ASME Journal of Heat Transfer, 108, 485-488.
http://dx.doi.org/10.1115/1.3246958 - 3. Nelson, D.J. and Wood, B.D. (1989) Fully Developed Combined Heat and Mass Transfer Natural Convection between Parallel Plates with Asymmetric Boundary Conditions. International Journal of Heat and Mass Transfer, 32, 1789-1792.
http://dx.doi.org/10.1016/0017-9310(89)90060-4 - 4. Hamadah, T.T. and Wirtz, R.A. (1991) Analysis of Laminar Fully Developed Mixed Convection in a Vertical Channel with Opposing Buoyancy. ASME Journal of Heat Transfer, 113, 507-510.
http://dx.doi.org/10.1115/1.2910593 - 5. Kou, H.S. and Huang, D.K. (1997) Fully Developed Laminar Mixed Convection through a Vertical Annular Duct Filled with Porous Media. International Journal of Heat and Mass Transfer, 24, 99-110.
http://dx.doi.org/10.1016/S0735-1933(96)00109-1 - 6. Boulama, K. and Galanis, N. (2004) Analytical Solution for Fully Developed Mixed Convection between Parallel Vertical Plates with Heat and Mass Transfer. ASME Journal of Heat Transfer, 126, 381-388.
http://dx.doi.org/10.1115/1.1737774 - 7. Umavathi, J.C. and Malashetty, M.S. (2005) Magnetohydrodynamic Mixed Convection in a Vertical Channel. International Journal of Non-Linear Mechanics, 40, 91-101.
http://dx.doi.org/10.1016/j.ijnonlinmec.2004.05.018 - 8. Chen, Y.C., Chung, J.N., Wu, C.S. and Lue, Y.F. (2000) Non-Darcy Mixed Convection in a Vertical Channel Filled with a Porous Medium. International Journal of Heat and Mass Transfer, 43, 2421-2429.
http://dx.doi.org/10.1016/s0017-9310(99)00299-9 - 9. Muralidhar, M. (1989) Mixed Convection Flow in a Saturated Porous Annulus. International Journal of Heat and Mass Transfer, 32, 881-888.
http://dx.doi.org/10.1016/0017-9310(89)90237-8 - 10. Hadim, A. and Chen, G. (1994) Non-Darcy Mixed Convection in a Vertical Porous Channel. Journal of Thermophysics and Heat Transfer, 8, 805-808.
- 11. Vafai, K. and Kim, S.J. (1989) Forced Convection in a Channel with a Porous Medium: An Exact Solution. Journal of Heat Transfer, 111, 1103-1106.
http://dx.doi.org/10.1115/1.3250779 - 12. Nadeem, S. and Akbar, N.S. (2009) Effects of Heat Transfer on the Peristaltic Transport of MHD Newtonian Fluid with Variable Viscosity: Application of Adomian Decomposition Method. Communications in Non-Linear Sciences and Numerical Simulation, 14, 3844-3855.
http://dx.doi.org/10.1016/j.cnsns.2008.09.010 - 13. Nield, D.A., Junqueira, S.L.M. and Large, J.L. (1996) Forced Convection in a Fluid-Saturated Porous-Medium Channel with Isothermal or Isoflux Boundaries. Journal of Fluid Mechanics, 322, 201-214.
http://dx.doi.org/10.1017/S0022112096002765 - 14. Beckett, P.M. (1980) Combined Natural and Forced Convection between Parallel Vertical Walls. SIAM Journal on Applied Mathematics, 39, 372-384.
http://dx.doi.org/10.1137/0139031 - 15. Chamkha, A.J. (2002) On Laminar Hydromagnetic Mixed Convection Flow in a Vertical Channel with Symmetric and Asymmetric Wall Heating Conditions. International Journal of Heat and Mass Transfer, 45, 2509-2525.
http://dx.doi.org/10.1016/S0017-9310(01)00342-8 - 16. Khan, M., Hyder Ali, S., Hayat, T. and Fetecau, C. (2008) MHD Flows of a Second Grade Fluid between Two Side Walls Perpendicular to a Plate through a Porous Medium. International Journal of Non-Linear Mechanics, 43, 302-319.
http://dx.doi.org/10.1016/j.ijnonlinmec.2007.12.016 - 17. Wazwaz, A.M. and El-Sayed, S.M. (2001) A New Modified of the Adomian Decomposition Method for Linear and Nonlinear Operators. Applied Mathematics and Computation, 122, 393-405.
http://dx.doi.org/10.1016/S0096-3003(00)00060-6 - 18. Wazwaz, A.M. (2006) The Modified Decomposition Method for Analytic Treatment of Differential Equations. Applied Mathematics and Computation, 173, 165-176.
http://dx.doi.org/10.1016/j.amc.2005.02.048 - 19. Barletta, A. and Zanchini, E. (1999) On the Choice of Reference Temperature for Fully Developed Mixed Convection in a Vertical Channel. International Journal of Heat and Mass Transfer, 42, 3169-3181.
http://dx.doi.org/10.1016/S0017-9310(99)00011-3
Nomenclature
Da Modified Darcy number, defined in Equation (1)
F Forchheimer number, defined in Equation (1)

g Acceleration due to gravity
Gr Grashof number or free convection parameter, defined in Equation (1)


m wall temperature ratio, defined in Equation (1)

P constant pressure gradient,
p Dimensionless fluid pressure defined in Equation (1)
Q dimensionless source/sink parameter defined in Equation (1)





u Dimensionless velocity component

x, y Dimensionless Cartesian coordinates

Greek Symbols



























