Open Journal of Fluid Dynamics
Vol.4 No.2(2014), Article
ID:47100,15
pages
DOI:10.4236/ojfd.2014.42017
A Note on Hydromagnetic Flow of an Oldroyd-B Fluid near an Infinite Plate Induced by Half Rectified Sine Pulses
Arun Kumar Ghosh1, Sanjib Kumar Datta2, Pulakesh Sen3
1Jadavpur University, Kolkata, India
2Department of Mathematics, University of Kalyani, Kalyani, India
3Department of Mathematics, D. N. C. College, Aurangabad, India
Email: akg10143@yahoo.co.in, sanjib_kr_datta@yahoo.co.in, psendnc2011@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 March 2014; revised 8 April 2014; accepted 16 May 2014
ABSTRACT
An initial value problem concerning the motion of an incompressible, electrically conducting, viscoelastic Oldroyd-B fluid bounded by an infinite rigid non-conducting plate is solved. The unsteady motion is generated impulsively from rest in the fluid due to half rectified sine pulses subjected on the plate in its own plane in presence of an external magnetic field. It is assumed that no external electric field is acting on the system and the magnetic Reynolds number is very small. The operational method is used to obtain exact solutions for the fluid velocity and the shear stress on the wall. Quantitative analysis of the results is presented with a view to disclose the simultaneous effects of the external magnetic field and the fluid elasticity on the flow and the wall shear stress for different periods of pulsation of the plate. It is also shown that the classical and hydromagnetic Rayleigh solutions appear as the limiting cases of the present analysis.
Keywords:Hydromagnetic, Pulsatile Flow, Oldroyd-B Fluid, Contour Integral

1. Introduction
The fluid flow generated by pulsatile motion of the boundary is found to have important applications in aerospace science, nuclear fusion, astrophysics, atmospheric science, cosmical gas dynamics, seismology and physiological fluid dynamics. Ghosh [1] examined the motion of an incompressible viscous fluid in a channel bounded by two coaxial cylinders when the inner cylinder is set in motion by the pulses of longitudinal impulses. Subsequently, Chakraborty and Ray [2] studied the unsteady magnetohydrodynamic coquette flow between two parallel plates when the upper plate is set in motion impulsively from rest by random pulses subjected on it. Makar [3] presented the solution of magnetohydrodynamic flow between two parallel plates when the velocity tooth pulses are imposed on the upper plate to initiate the fluid motion impulsively from rest and the induced magnetic field is neglected. Bestman and Njoku [4] constructed the solution of the same problem as that of author [3] without ignoring the effect of induced magnetic field and using the methodology different from that of author [3] to arrive at the solution of the problem. Ghosh and Sarkar [5] considered the hydromagnetic channel flow of an electrically conducting dusty fluid induced by tooth pulses. These authors have shown that the methodology followed by the authors [3] [4] leads to the same exact solution of the problem. Ghosh and Ghosh [6] solved the same problem as that of authors [5] replacing the boundary condition at the upper plate of the channel by rectified sine pulses instead of tooth pulses as encountered by authors [5] . In a subsequent paper Ghosh and Ghosh [7] also examined the hydromagnetic flow of a two-phase fluid near a pulsating plate with a view to its application in the analysis of suspension boundary layers. On the other hand, Datta & Datta [8] [9] discussed the heat transfer to pulsatile flow of a dusty fluid in pipes and channels with a view to their application in the analysis of blood flow. In spite of the above works, the study of pulsatile flows in Oldroyd-B fluids is equally important because these fluids encounter both elasticity and memory effects exhibited by most polymeric and biological liquids. Tanner [10] solved the classical Rayleigh problem associated with an Oldroyd-B fluid while Ghosh and Mitra [11] constructed solutions of Stokes problem for a linear viscoelastic fluid of Oldroyd-B type. Ghosh and Debnath [12] analysed the heat transfer to pulsatile flow of a viscoelastic Oldroyd-B fluid between two parallel plates. Exact solutions for some simple flows of an Oldroyd-B fluid were given by Rajagopal and Bhatnagar [13] . Some simple flows of an Oldroyd-B fluid were discussed by Hayat, Siddiqui & Asghar [14] . Exact solutions of MHD flows of an Oldroyd-B fluid over an infinite oscillatory plate were obtained by Hayat et al. [15] . Stokes’ first problem for an Oldroyd-B fluid in a porous half space was solved by Tan and Masuoka [16] . Javadzadegan et al. [17] discussed the pulsatile flow of viscous and viscoelastic fluids in constricted tubes with a view to analyse the viscoelastic behaviour of blood using the Oldroyd-B fluid model. Most recently, Ghosh and Sana [18] presented solutions of hydromagnetic rotating flow of an Oldroyd-B fluid near an oscillating plate. In the present paper, we intend to construct solution of hydromagnetic flow of an Oldroyd-B fluid near an infinite plate induced by half rectified sine pulses with a view to its application in more generalised physical situations. It appears that besides various applications of pulsatile flow mentioned above, the present investigation seems to be useful in the analysis of suspension boundary layers, the blood flow during irregular heartbeats, flows in the liquid core of the earth during earthquakes, spreading of protective coating on electronic and optical devices and in the detection of magnetic effect on electrically conducting flows of biological fluids.
The problem is concerned with the unsteady hydromagnetic flow of a semi-infinite expanse of an incompressible, electrically conducting viscoelastic Oldroyd-B fluid bounded by an infinite rigid non-conducting plate. The motion is supposed to generate from rest in the fluid due to unidirectional motion of the plate in its own plane caused by half rectified sine pulses applied periodically on it. The operational method is used to obtain exact solutions for the fluid velocity and the shear stress exerted by the fluid on the pulsating plate. The quantitative analysis is made to examine the influence of the elasticity, the magnetic field and the time-period of pulsation on the fluid velocity and also on the wall shear stress. It is shown that hydromagnetic and hydrodynamic Rayleigh solutions appear as special cases of the present analysis.
2. Basic Equations
The constitutive equations for an Oldroyd-B fluid [14] [15] are
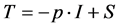 (2.1)
(2.1)
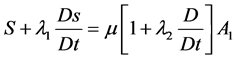 (2.2)
(2.2)
where T = Cauchy stress tensor, p = fluid pressure, I = identity tensor, S = extra stress tensor and µ = viscosity coefficient, λ1 = relaxation time, λ2 = retardation time (assumed constants).
The tensor A1 is defined as
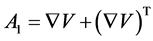 (2.3)
(2.3)
In a Cartesian system, 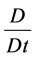 (upper convected time derivative) operating on any tensor B1 is
(upper convected time derivative) operating on any tensor B1 is
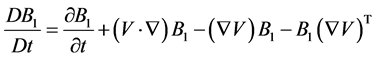 (2.4)
(2.4)
It is to be mentioned here that this model includes the viscous fluid as a particular case for λ1 = λ2, the Maxwell fluid when λ2 = 0 and an Oldroyd-B fluid when 0 < λ2 < λ1 < 1.
The stress equations of motion for an incompressible electrically conducting Oldroyd-B fluid in presence of an external magnetic field are
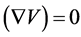 (2.5)
(2.5)
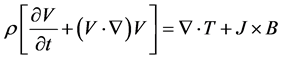 (2.6)
(2.6)
 (2.7a)
(2.7a)
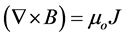 (2.7b)
(2.7b)
 (2.8a)
(2.8a)
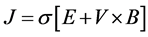 (2.8b)
(2.8b)
where V(u, v, w) = fluid velocity, ρ = fluid density, J = current density, B = magnetic flux density, E = electric field, µo = magnetic permeability (assumed constant), and σ = electrical conductivity (assumed finite).
It is to be noted here that the electromagnetic effect entering in Equations (2.6) to (2.8b) are approximation under the assumption of the small magnetic Reynolds number. More precisely, the above equations hold good if the condition V = σL, in which V is the characteristic velocity and L is the characteristic scale of motion, is satisfied. It is also noteworthy that the inequality given above holds in many cases of interest.
3. Formulation of the Problem
In this problem, we consider the motion of a viscoelastic electrically conducting Oldroyd-B fluid where the xaxis is taken in the direction of flow with the origin at the plate and y-axis perpendicular to it. The initial motion is generated in the fluid due to the half rectified sine pulses applied on the plate. A uniform magnetic field of strength B0 is acting parallel to y-axis. We assume that no external electric field is acting on the fluid and the magnetic Reynolds number is very small. This implies that the current in the fluid is mainly due to the induced electric field and the applied magnetic field remains essentially unaltered by the electric current flowing in the fluid. We also assume that the induced magnetic field produced by the motion of the fluid is negligible compared to the applied magnetic field so that the Lorentz force term in Equation (2.6) becomes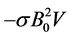 . Since the motion is a plain one and the plate is infinitely long, we assume that all the physical variables are independent of x and z. Then from the equation of continuity (2.5) and from the physical conditions of the problem, we take
. Since the motion is a plain one and the plate is infinitely long, we assume that all the physical variables are independent of x and z. Then from the equation of continuity (2.5) and from the physical conditions of the problem, we take
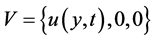 (3.1a)
(3.1a)
and
 (3.1b)
(3.1b)
The equations of motion in (2.6) then reduces to
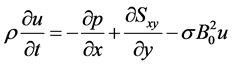 (3.2a)
(3.2a)
 (3.2b)
(3.2b)
 (3.2c)
(3.2c)
It follows from Equations (2.2), (3.1a) and (3.1b) that
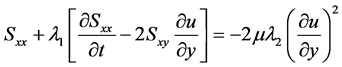 (3.3a)
(3.3a)
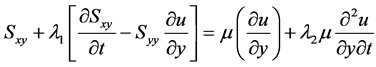 (3.3b)
(3.3b)
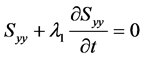 (3.3c)
(3.3c)
The Equation (3.3c) gives
 (3.4)
(3.4)
where A(y) is an arbitrary function of y. But Syy is known to be zero for t < 0. This implies that A(y) must be zero. Hence Syy is zero always. Consequently, from (3.2a) and (3.3b) and in the absence of the pressure gradient along x direction, we get
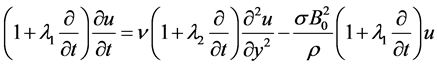 (3.5)
(3.5)
which on introducing the dimensionless quantities given by 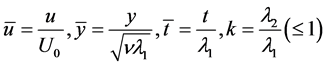 and
and 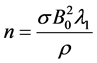 and on dropping the bars, we get
and on dropping the bars, we get
 (3.6)
(3.6)
The problem now reduces to solving Equation (3.6) subject to initial and boundary conditions:
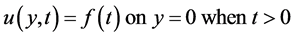 (3.7a)
(3.7a)
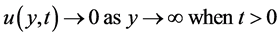 (3.7b)
(3.7b)
and
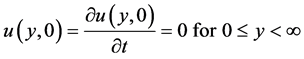 (3.7c)
(3.7c)
where f(t) representing the half rectified sine pulses, as shown in Figure 1, is a periodic function of time with period T.
4. Solution of the Problem
In view of the nature of f(t) (as shown in Figure 1) mentioned above the mathematical form of u(0, t) may be written as
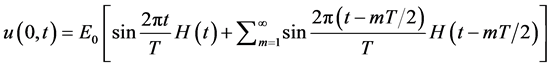 (4.1)
(4.1)
where H(t) is the Heaviside unit step function defined as
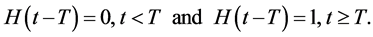
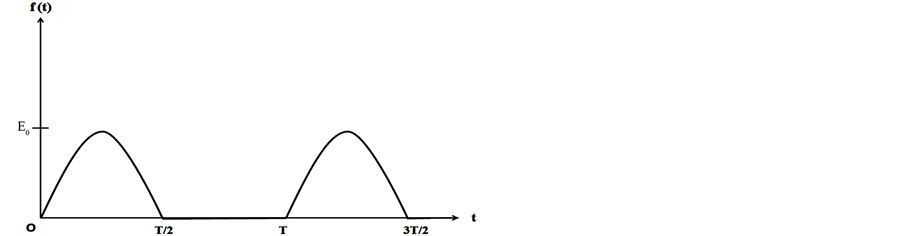
Figure 1. Half-rectified sine pulses with period T.
The use of Laplace transform method for the solution of the Equation (3.6) with initial conditions in Equation (3.7c), provides the transformed equation for the fluid velocity in the form
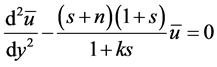 (4.2)
(4.2)
with the boundary conditions
 (4.3)
(4.3)
and
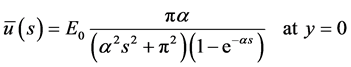 (4.4)
(4.4)
where s is the Laplace Transform variable and α = T/2.
The transformed solution for the fluid velocity 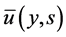 becomes
becomes
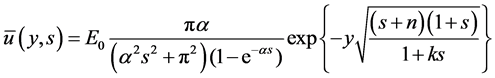 (4.5)
(4.5)
The inversion of Equation (4.5) gives
 (4.6)
(4.6)
The inversion integral has poles at 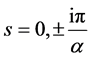 and a series of poles at
and a series of poles at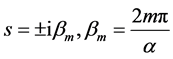 ,
, 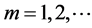 and branch points at
and branch points at 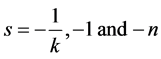 as shown in the contour drawn in Figure 2 in the complex s-plane.
as shown in the contour drawn in Figure 2 in the complex s-plane.
Evaluating Equation (4.6) with the help of Cauchy’s Residue theorem applied to the contour in Figure 2, we get
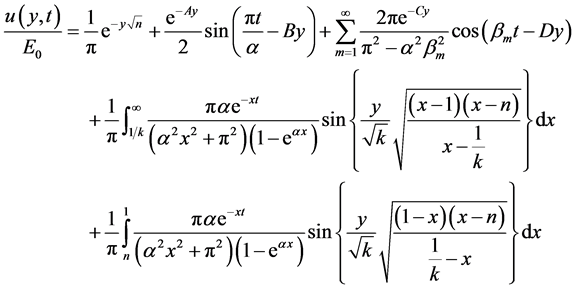 (4.7)
(4.7)
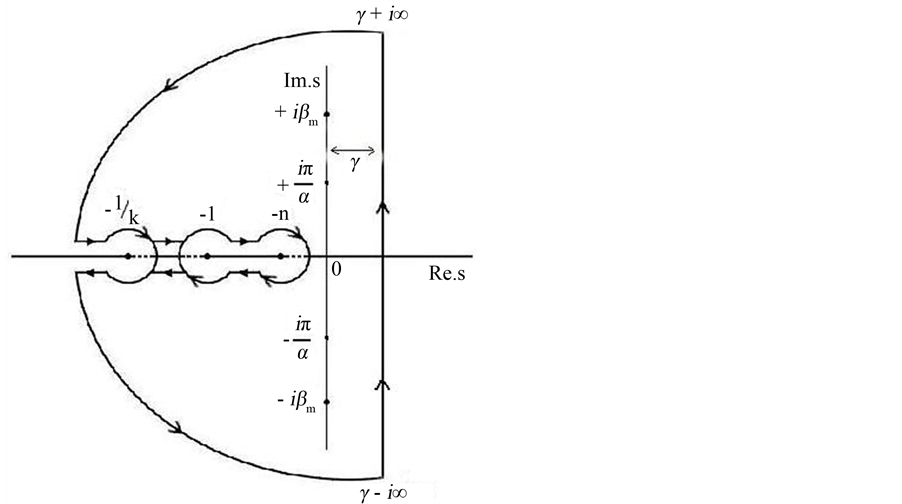
Figure 2. The Contour integral path for the Equation (4.7) showing the points of singularity and branch points.
where ,
, 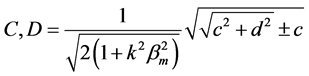
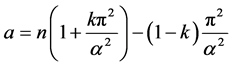 ,
, 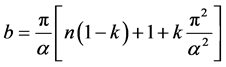 ,
, 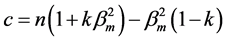
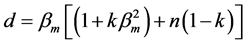 ,
,  and
and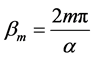 .
.
On the other hand, the solution corresponding to the classical viscous fluid can be obtained from Equation (4.7) in the limit k → 1. This solution is given by
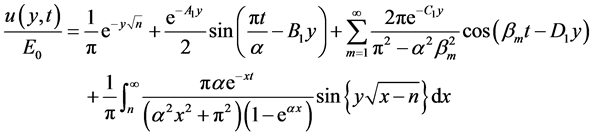 (4.8)
(4.8)
where 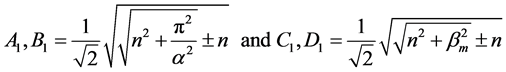
Further, when E0 = π and T → 0, the Equation (4.7) reduces to
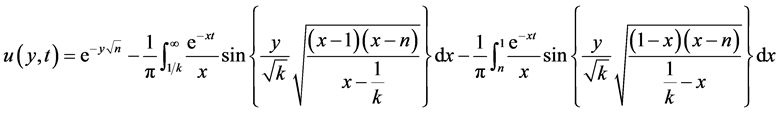 (4.9)
(4.9)
which describes the Hydromagnetic Rayleigh solution for an Oldroyd-B fluid and coincides with the findings of authors Ghosh and Mitra [11] .
On by putting k = 1 in the Equation (4.9), we get
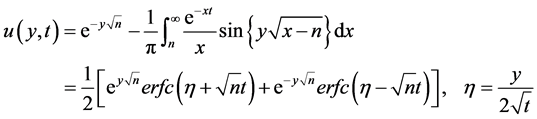 (4.10)
(4.10)
which is the well-known solution of the hydromagnetic Rayleigh problem (cf. [19] ).
On the other hand, if n → 0 we get from the Equation (4.10) the classical Rayleigh solution as
 (4.11)
(4.11)
The fluid velocity given by the Equation (4.7) attains the steady-state in the limit t→∞ and the ultimate flow becomes
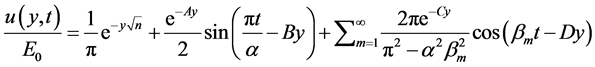 (4.12)
(4.12)
The ultimate steady flow given by Equation (4.12) contains the effect of both the elasticity and the magnetic field and consists of several distinct boundary layers in the vicinity of the plate due to the effect of pulsation.
One is a Hartman layer of thickness of the order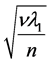 , the other is a Stokes-Hartman layer of thickness of order
, the other is a Stokes-Hartman layer of thickness of order and the rests are multiple Stokes-Hartman boundary layers of thicknesses of order
and the rests are multiple Stokes-Hartman boundary layers of thicknesses of order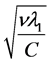 .
.
Since C > A > n, the thickness of the Hartman layer is greater than the Stokes-Hartman layers which decrease with the increase of the elastic parameter (k) and the magnetic field (n). However, in the limit T →0 (α → 0, βm → ∞) i.e. in absence of pulsation, all the boundary layers coalesce into a single classical Hartman layer of thickness of order 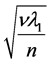 which appears in the vicinity of the plate. This shows that the elasticity of the fluid can manifest its effect only in presence of pulsation.
which appears in the vicinity of the plate. This shows that the elasticity of the fluid can manifest its effect only in presence of pulsation.
The exact solution for the stress on the plate y = 0, in dimensionless form, is given by
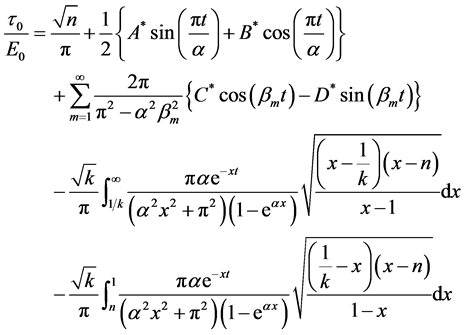 (4.13)
(4.13)
where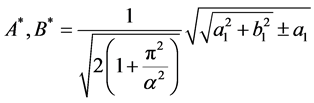 ,
, 
 ,
, 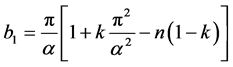 ,
, 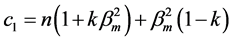
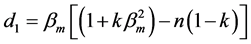 ,
, 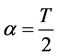 and
and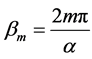 .
.
which when k → 1 yields
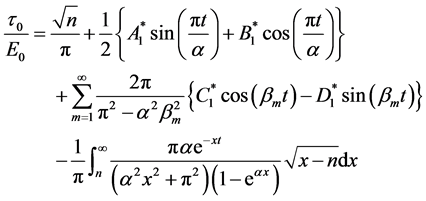 (4.14)
(4.14)
where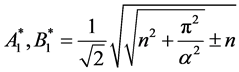 ,
, 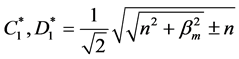
On the other hand, if T → 0 and E0 = π, we have from Equation (4.13), the shear stress corresponding to Oldroyd-B fluid on the non-pulsating wall becomes
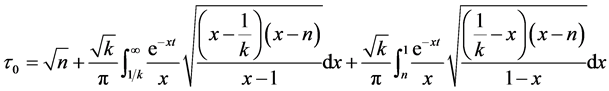 (4.15)
(4.15)
which when k → 1 provides the shear stress on the wall corresponding to hydromagnetic Rayleigh problem as
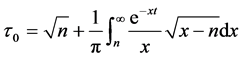 (4.16)
(4.16)
and in the limit n → 0, yields the familiar result
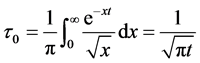 (4.17)
(4.17)
5. Numerical Results
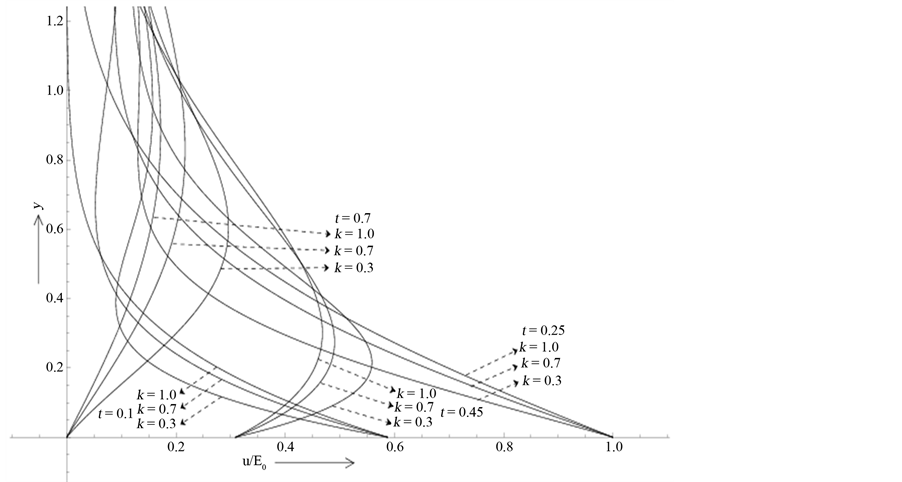
Unlike the generating flow in Rayleigh problem and the oscillatory result given by Stokes solution the nature of the pulses imparted on the plate produces both developing and retarding motions propagating unidirectionally in the fluid during the duration of each pulse. The quantitative analysis of the result (4.7) representing the fluid velocity is shown in Figure 3(a) for the increasing motions corresponding to t = 0.1 and 0.25 and the retarding motions for t = 0.45 and 0.7 when T = 1.0, n = 0.1 and the elastic parameter k assuming the values 0.3, 0.7 and 1.0 in each case. It appears that the fluid velocity near the plate increases with k when the motion is developing and decreases with k when the motion is retarding. For example, at y = 0.2, n = 0.1, T = 1.0, and k changes from 0.3 to 0.7, the fluid velocity increases by 46.4% and 17.3% respectively when t = 0.1, 0.25. Similarly, at y = 0.2, n = 0.1, T = 1.0 and k changes from 0.3 to 0.7, the fluid velocity decreases by 13.95% and 38.75% respectively when t = 0.45, 0.7. Such a result is expected in the presence of pulses although it is not true in the non-pulsatile case.
We also observe that the above increasing and decreasing effects produced by the elastic parameter k is further enhanced with the increase of magnetic field (n). It is to be noted here that the value of the elastic parameter k = 1, represents the Newtonian case and the fluid will be more and more viscoelastic for lesser and lesser values of k. On the other hand, the magnetic field (n) produces damping effect on the flow irrespective of its nature. This fact is presented in Figure 3(b). Similarly, the effects of the magnetic field and the elasticity of the fluid associated with both the increasing and decreasing motions for T = 0.5 and T = 2.0 are shown respectively in Figure 4(a) and Figure 4(b). A comparative study of the developing flow produced by the impulsively moved plate and the pulsatile plate is shown in Figure 4(c) for T = 0 and T = 1.0 respectively. It is seen that the velocity of developing flow near the plate in the pulsatile case (T = 1.0) is higher than that produced by the impulsively moved plate (T = 0). Moreover, contrary to pulsatile case the fluid velocity near the plate diminishes with the increase of the fluid elasticity (k) in the non-pulsatile case although magnetic field has a damping effect on both types of flow. The solution for the hydromagnetic and the classical Rayleigh solutions corresponding to k = 1, n = 0.9 and k = 1, n = 0 respectively are represented graphically in Figure 4(c). The effects of k and non the developing and retarding flows with the increase of time period of pulsation (T) are presented in Figure 5(a) and
 (a)
(a)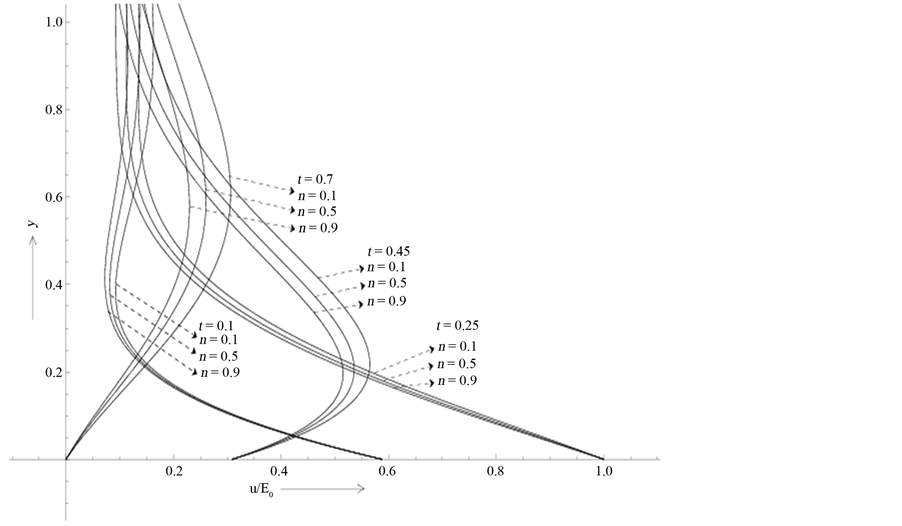 (b)
(b)
Figure 3. (a) Effect of elasticity (k) on the fluid velocity for the developing and retarding motions when n = 0.1 and T = 1.0; (b) Effect of the magnetic field (n) on the fluid velocity for the developing and retarding motions when k = 0.3 and T = 1.0.
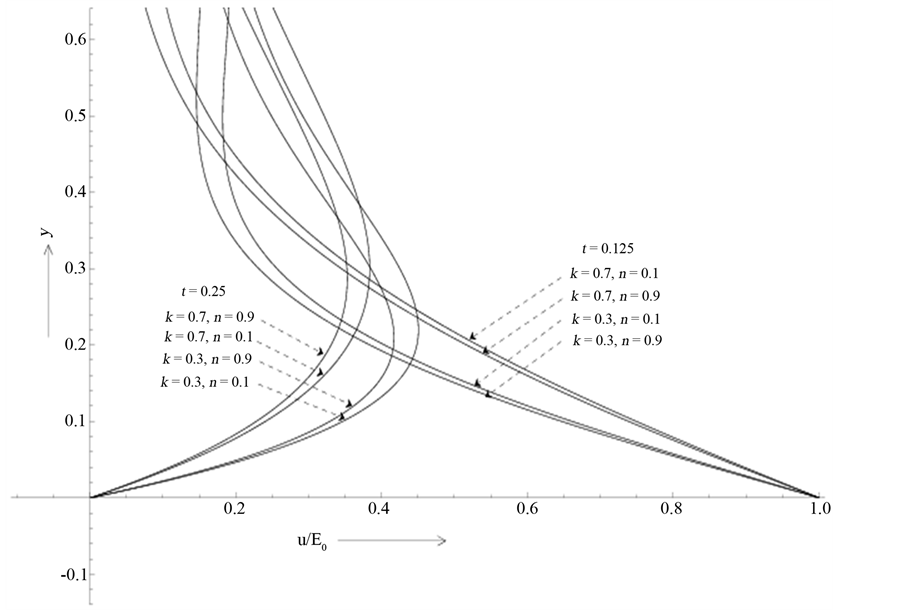
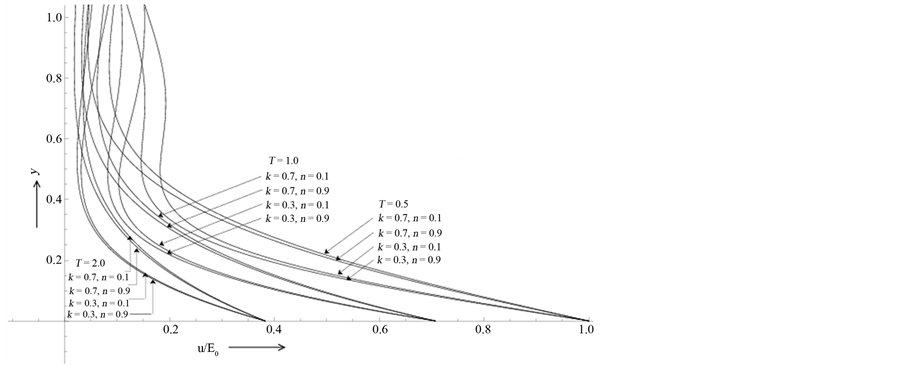
Figure 5(b). It is found that the developing flows gradually diminishes with the increase of time period T while a reverse effect is found in the case of retarding motions. The steady-state solutions for fixed values of n and k and for increasing values of T are shown in Figure 6. It is clearly reflected from the nature of the velocity profiles shown in Figure 6 that the structure of the hydromagnetic boundary layer is significantly different from those of pulsatile boundary layers. The thicknesses of the pulsatile boundary layers near the plate decrease with the increase of time period of pulsation which is expected from steady-state solution.
 (a)
(a)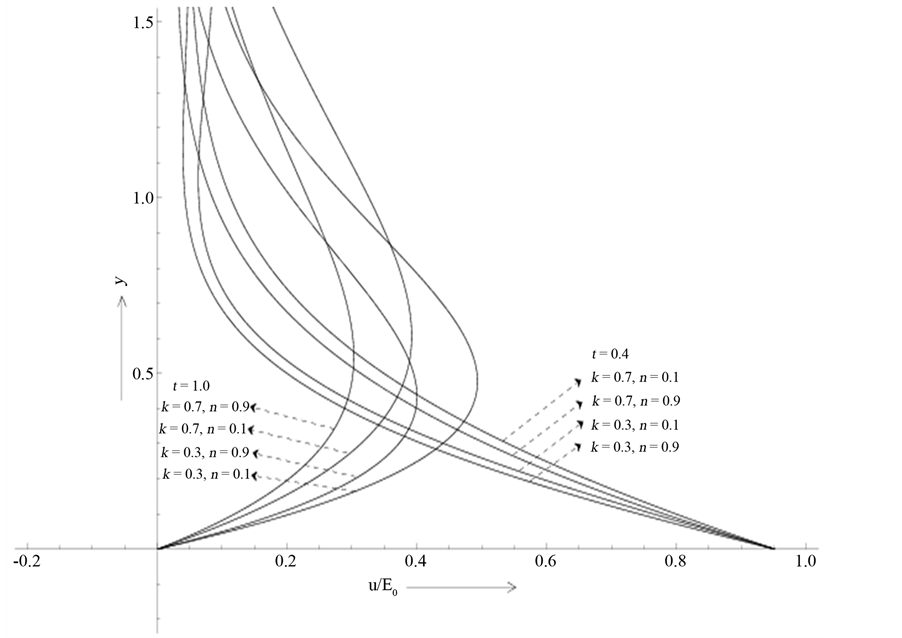 (b)
(b)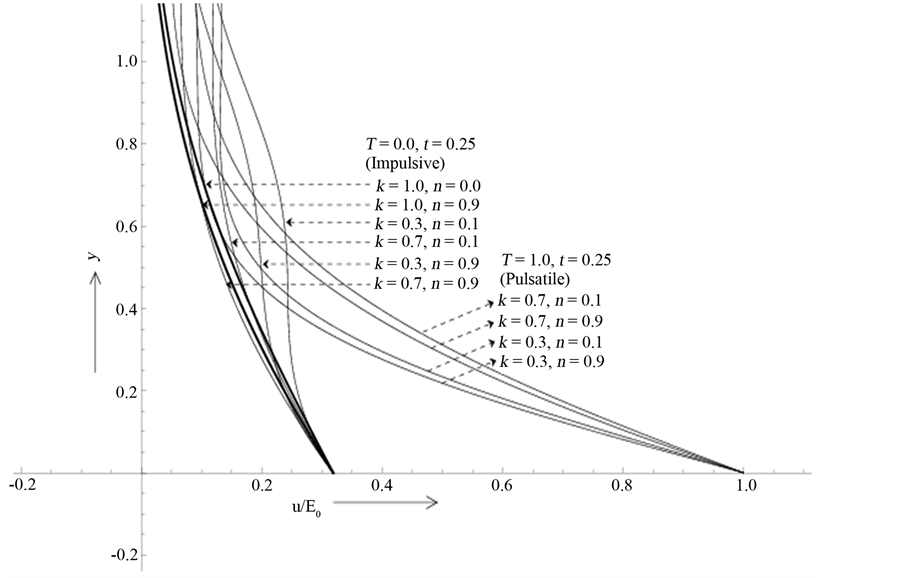 (c)
(c)
Figure 4. (a) Effects of the magnetic field (n) and the elasticity (k) on the fluid velocity for the developing and retarding flows when T = 0.5; (b) Effects of the magnetic field (n) and the elasticity (k) on the fluid velocity for the developing and retarding flows when T = 2.0; (c) Effects of the magnetic field (n) and the elasticity (k) on the fluid velocity for both the Pulsatile and Impulsive motion of the plate at t = 0.25.
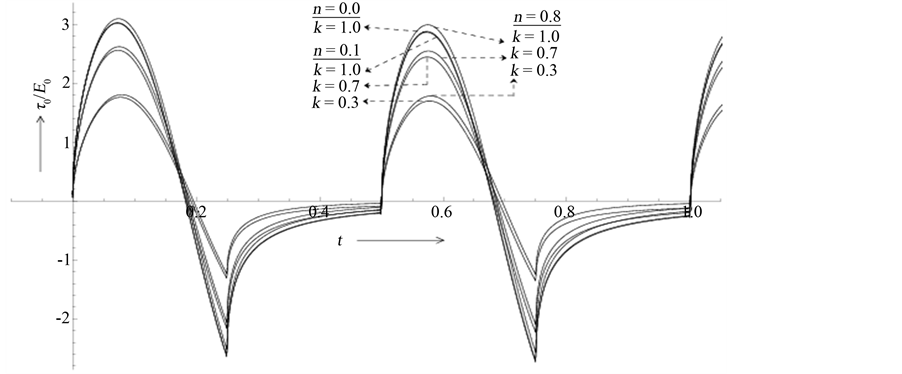
The distribution of shear stress on the plate is plotted in the Figures 7(a)-(c) with the advancement of time, respectively, for the cases T = 0.5, 1.0 and 2.0. The limiting result associated with the Rayleigh stress at T = 0.0 is presented in Figure 7(d). The effects of the elasticity (k) and the magnetic field (n) have also considered in each case. It is seen that the wall shear stress fluctuates with time in a manner similar to that of the pulses on the plate for all non-zero values of the time period (T). Moreover, unlike Rayleigh-stress, the shear stress on the plate in each case becomes negative during the period of rectification. This is expected because at the beginning of rectification, the decelerating motion of the plate starts which drives the fluid towards its destination by exerting shear stress in opposite direction (negative shear stress). Such a situation prevail still the plate acquires sufficient momentum to overcome the negative shear stress during its next accelerated motion. Besides, the maximum value of the shear stress is found to occur at about t = 0.075λ1, 0.15λ1 and 0.3λ1 respectively when T = 0.5, 1.0 and 2.0. Similar values can also be obtained for minimum values of shear stress on the plate which differs with T. In general, the stress on the plate decreases with the increase of the time period of pulsation (T) irrespective of the nature of the flow. On the other hand, as in the case of impulsively started motion, increase of the elastic parameter (k) increases the stress which is further enhanced with the increase of the magnetic field (n) when the flow is developing. However, a reverse effect is found when the motion is retarding.
6. Conclusion
The present problem is concerned with the investigation of unsteady motion generated from rest in a semi-infinite expanse of an Oldroyd-B fluid due to multiple frequency unidirectional motion of the plate bounding the fluid instead of that generated impulsively from rest by the movement of the plate with constant velocity (Stokes first problem) orby oscillation of the plate in its own plane with a given frequency (Stokes second problem). As a result, the present problem differs widely from those mentioned above as it provides a unidirectional positive flow for all values of time and Stokes first problem both in hydrodynamic and hydromagnetic situations emerges
 (a)
(a)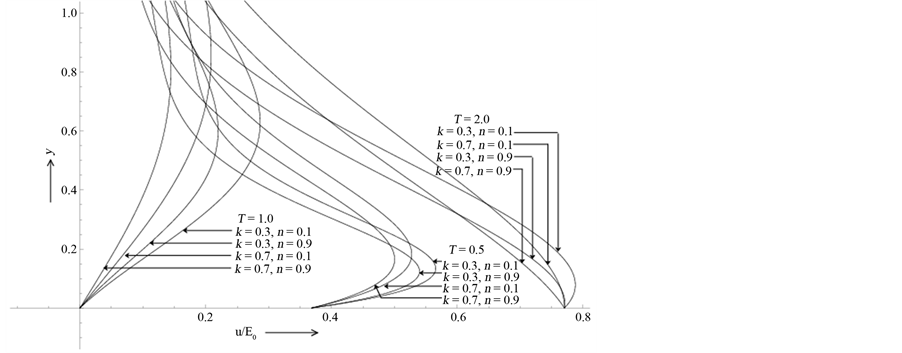 (b)
(b)
Figure 5. (a) Effects of the magnetic field (n) and the elasticity (k) on the fluid velocity for the developing motion when T = 0.5, 1.0, 2.0 at t = 0.125; (b) Effects of the magnetic field (n) and the elasticity (k) on the fluid velocity for the retarding motion when T = 0.5, 1.0, 2.0 at t = 0.72.
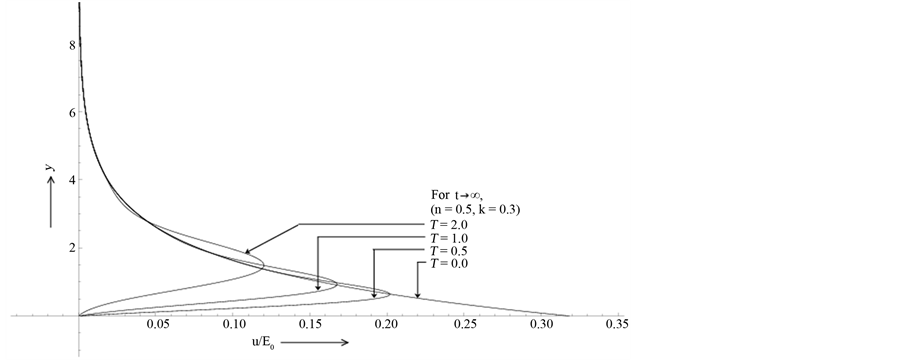
Figure 6. The steady-state solution for the fluid motion at n = 0.5, k = 0.3 when T = 0.5, 1.0, 2.0 as t → ∞.
 (a)
(a)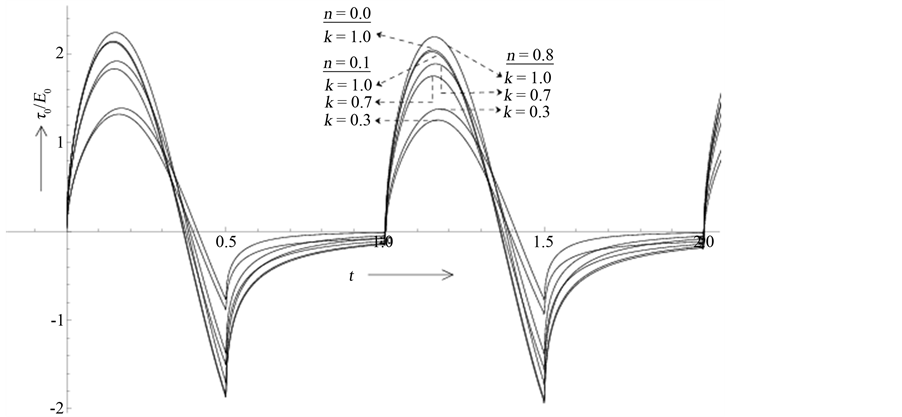 (b)
(b)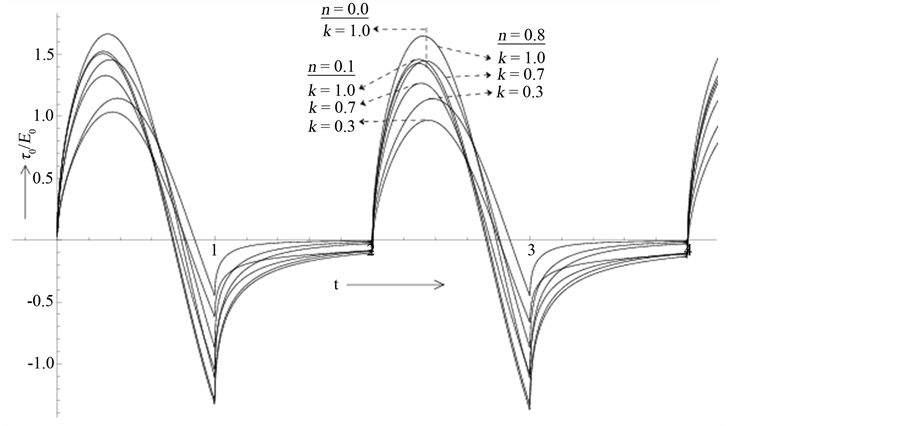 (c)
(c) (d)
(d)
Figure 7. (a) Effects of the magnetic field (n) and the elasticity (k) on the shear stress at the plate y = 0 when T = 0.5; (b) Effects of the magnetic field (n) and the elasticity (k) on the shear stress at the plate y = 0 when T = 1.0; (c) Effects of the magnetic field (n) and the elasticity (k) on the shear stress at the plate y = 0 when T = 2.0; (d) Effects of the magnetic field (n) and the elasticity (k) on the shear stress at the plate y = 0 when T = 0.0.
as special cases of it. The present problem although idealized bears a good resemblance with the blood flow in large arteries during irregular heartbeats, some atmospheric and oceanic flows driven by pressure pulses, air flows during traffic movements, movement of aircraft in some strategic positions and geophysical flows during earthquakes. Consequently the present study will be helpful to discuss the structure of the boundary layers and the effects of flow parameters associated with the pulsatile motion of viscoelastic fluids. Additionally, as the major findings of the present analysis we notice that in the presence of pulsation, the elastic parameter increases the developing flow near the plate, whereas, in the absence of pulsation such a motion decreases with the increase of the elasticity (k). We further notice that the retarding motion near the plate caused by pulsation decreases with the increase of the elastic parameter k. In all cases, the effect of (k) on the flow is enhanced with the increase of n, although the magnetic field (n) has an overall effect of damping the motion irrespective of its nature. The intensity of the pulsatile flow near the plate is always greater than the impulsively generated flow. The magnetic field and the fluid elasticity require some time to exert their influence on the wall shear stress for all values of time period (T). Finally, the elastic parameter (k) and the magnetic field (n) increase the stress value for all values of T which is much pronounced near the ends of the accelerated and retarded motions for the pulsatile case and near the beginning of the developing motion when the flow started impulsively from rest. However, for fixed values of k and n the stress value of the pulsatile flow decreases with the increase of the time period (T).
References
- Ghosh, A.K. (1965) Flow of Viscous Liquid Set up between Two Co-Axial Cylinders Due to Pulses of Longitudinal Impulses Applied on the Inner Cylinder. Journal of Science and Engineering Research, 9, 222.
- Chakraborty, A. and Ray, J. (1980) Unsteady Magnetohydrodynamic Couetteflow between Two Plates When One of the Plates Is Subjected to Random Pulses. Journal of the Physical Society of Japan, 48, 1361-1364. http://dx.doi.org/10.1143/JPSJ.48.1361
- Makar, M.N. (1987) Magnetohydrodynamic Flow between Two Plates When One of the Platesis Subjected to Tooth Pulses. Acta Physica Polonica, A71, 995.
- Bestman, A.R. and Njoku, F.I. (1988) On Hydromagnetic Channel Flow Induced by Toothpulses. Miramare-Trieste.
- Ghosh, A.K. and Sarkar, K. (1995) On Hydromagnetic Channel Flow of a Dusty Fluid Induced by Tooth Pulses. Journal of the Physical Society of Japan, 64, 1489-1500. http://dx.doi.org/10.1143/JPSJ.64.1489
- Ghosh, S. and Ghosh, A.K. (2004) On Hydromagnetic Channel Flow of a Particulate Suspension Induced by Rectified Sine Pulses. Journal of the Physical Society of Japan, 73, 1506-1513. http://dx.doi.org/10.1143/JPSJ.73.1506
- Ghosh, S. and Ghosh, A.K. (2004) On Hydromagnetic Flow of a Two-Phase Fluid near a Pulsating Plate. Indian Journal of Pure and Applied Mathematics, 36, 529.
- Datta, N., Dalal, D.C. and Mishra, S.K. (1993) Unsteady Heat Transfer to Pulsatile Flow of a Dustyviscous Incompressible Fluid in a Channel. International Journal of Heat and Mass Transfer, 36, 1783-1788. http://dx.doi.org/10.1016/S0017-9310(05)80164-4
- Datta, N. and Dalal, D.C. (1995) Pulsatile Flow and Heat Transfer of a Dusty Fluid through an Infinitely Long Annular Pipe. International Journal of Multiphase Flow, 21, 515-528. http://dx.doi.org/10.1016/0301-9322(94)00064-Q
- Tanner, R.I. (1962) Note on the Rayleigh Problem for a Viscoelastic Fluid. Zeitschrift fur Angewandte Mathematik und Physik, 8, 573.
- Ghosh, A.K. and Mitra, S. (1977) On Stokes’ Problems for Linear Viscoelastic Fluids. Bulletinde L’Academie Polonaise des Sciences, 25, 55.
- Ghosh, A.K. and Debnath, L. (1992) On Heat Transfer to Pulsatile Flow of a Viscoelastic Fluid. Acta Mechanica, 93, 169-177. http://dx.doi.org/10.1007/BF01182582
- Rajagopal, K.R. and Bhatnagar, R.K. (1995) Exact Solutions for Some Simple Flows of an Oldroyd-B Fluid. Acta Mechanica, 113, 233-239. http://dx.doi.org/10.1007/BF01212645
- Hayat, T., Siddiqui, A.M. and Asghar, S. (2001) Some Simple Flows of an Oldroyd-B Fluid. International Journal of Engineering Science, 39, 135-147. http://dx.doi.org/10.1016/S0020-7225(00)00026-4
- Hayat, T., Hutter, K., Asghar, S. and Siddiqui, A.M. (2002) MHD Flows of an Oldroyd-B Fluid. Mathematical and Computer Modelling, 36, 987-995. http://dx.doi.org/10.1016/S0895-7177(02)00252-2
- Tan, W.C. and Masuoka, T. (2005) Stokes’ First Problem for an Oldroyd-B Fluid in a Porous Half Space. Physics of Fluids, 17, Article ID: 023101. http://dx.doi.org/10.1063/1.1850409
- Javadjzadegan, A., Esmaeili, M., Majidi, S. and Fakhimghanbarzadeh, B. (2009) Pulsatile Flow of Viscous and Viscoelastic Fluids in Constricted Tubes. Journal of Mechanical Science and Technology, 23, 2456-2467. http://dx.doi.org/10.1007/s12206-009-0713-9
- Ghosh, A.K. and Sana, P. (2009) On Hydromagnetic Rotating Flow of an Oldroyd-B Fluid near an Oscillating Plate. Zeitschrift für angewandte Mathematik und Physik, 60, 1135-1155. http://dx.doi.org/10.1007/s00033-009-8060-3
- Yang, H.T. and Healy, J.V. (1973) The Stokes Problem for a Conducting Fluid with Suspension of Particles. Applied Scientific Research, 21, 378.

