Open Journal of Applied Sciences
Vol.05 No.10(2015), Article ID:60775,9 pages
10.4236/ojapps.2015.510063
The Entropy Law and the Impossibility of Perpetual Economic Growth
Henrique N. Sá Earp1, Ademar R. Romeiro2
1Unicamp-Institute of Mathematics, Campinas, Brazil
2Unicamp-Institute of Economics, Campinas, Brazil
Email: arromeiro@gmail.com, henrique.saearp@ime.unicamp.br
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 August 2015; accepted 26 October 2015; published 29 October 2015
ABSTRACT
Every production-recycling iteration accumulates an inevitable proportion of its matter-energy in the environment, lest the production process itself will be a system in perpetual motion, violating the second law of Thermodynamics. Such high-entropy matter depletes finite stocks of ecosystem services provided by the ecosphere, hence is incompatible with the long-term growth in the material scale of the economic process. Moreover, the complex natural systems governing such stocks respond to depletion by possibly sudden environmental transitions, thus hindering markets' very ability to adapt to the new equilibrium conditions. Consequently, uncertainty of critical resilience thresholds constrains material economic growth.
Keywords:
Entropy, Perpetual Growth, Zero Growth, Ecosystem Resilience

The law that entropy always increases holds, I think, the supreme position among the laws of Nature. If someone points out to you that your pet theory of the universe is in disagreement with Maxwell’s equa- tions-then so much the worse for Maxwell’s equations. If it is found to be contradicted by observation-well, these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of thermodynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation.
Sir Arthur S. Eddington (1927)
1. Introduction
A systematic treatment of environment, or natural resources, as a production factor is relatively recent in economic literature. The pioneering work of Harold Hotelling on the economics of exhaustible resources [1] had a limited impact until the environmental awareness in the sixties, culminating with the publication of Limits to Growth (1972). Robert Solow’s much quoted Richard T. Ely Lecture [2] , reflecting the current state of the art on the subject, was built on it. Solow’s insights, in turn, have remained a reference in the mainstream literature, providing the theoretical arguments for the concept of “weak sustainability”.
The main issue he had proposed to deal with was not the exhaustibility of natural resources in itself as a limit to the economic process, but the optimal social management of stocks of non-renewable but essential resources. The Laws of Thermodynamics were invoked at the onset to explain why materials recycling could not prevent the eventual exhaustion of all non-renewable resources and, indeed, why eventually the whole life on earth would come to an end. Hotelling’s rule was seen as a necessary condition for efficiency, and therefore for social optimality, but not a sufficient one. There were reasons for Solow to expect market interest rates to surpass the social rate of time preference, leading to an exceedingly fast market consumption of exhaustible resources. Therefore corrective public intervention should be brought in to slow down and stretch out the exploitation of the resource pool. Moreover, there can also be several patterns of exploitation of the exhaustible-resource pool which obey Hotelling’s fundamental principle myopically in the short term, but are wrong in the long term, implying markets need a reasonably accurate view of the long-term prospects.
More specifically, Solow pointed two conditions that could guarantee intergenerational equity in the access to the exhaustible-resource pool in the long run: first, the likelihood of technical progress, especially natural resource-saving advances―what is called today ecological efficiency of the production process (e.g. some innovation reducing losses of ore in mining or smelting); second, the degree of substitutability of exhaustible resources by other factors of production, notably labor and reproducible capital (e.g. homeowners increasing expenditures on insulation to save on fuel costs, thus substituting fiberglass for heating oil).
These are empirical issues, doubtless, but there will be grounds to expect prolonged and substantial reductions in natural-resource requirements per unit of real output as well as “quite a lot of substitutability between exhaustible resources and renewable or reproducible resources”. Solow stressed in particular the importance of the latter, specifically as to reproducible resources, reminiscent perhaps of the laws of thermodynamics he had evoked to point to the limits of the former. Since then, a huge amount of empirical research has been done to find evidence of them in the economic process “decoupling” from its natural resource basis.
The ecological model behind Solow’s analytical effort fails to address all relevant ecological aspects at stake: his Laws of Thermodynamics apply only to ecological efficiency; the continual substitution of new natural resources for depleted ones has no thermodynamic consequence. Indeed that author neglects the second dimension of natural resources, as source of ecosystem services, which is inevitably impacted by the resulting increase of the mass-energy scale of the economic process.
What came to be known as “Economics of Pollution”, as distinguished from “Economics of Exhaustible Resources”, evolved to deal precisely with this second dimension. The work of Pigou on the concept of externalities [3] provided its theoretical basis. Economically, the specificity of this aspect derives from the absence of markets for ecosystem services, due to the public status of the ecosystems which provide them. To fix the problem, allowing markets to appear, the State must intervene either by pricing or establishing property rights over them. In so doing, market forces would lead to socially optimal paths of ecosystem services use, i.e. optimal pollution. There are no risks of potentially catastrophic losses of critical ecosystems in this model.
Furthermore, the same conditions that could guarantee intergenerational equity in access to the exhaustible resources pool in the long run would also imply equity of access to ecosystem services. Although renewable in principle, the latter can be treated as exhaustible because their stock at any given time is finite and can be destroyed by overuse. On the other hand, increases in ecological efficiency can prevent that, either reducing the waste generated by the productive process (“clean” technology), or substituting capital-intensive residue treatment facilities for the ecosystem service of waste absorption (“end-of-pipe” technology). Last, but indeed not least, even if an ecosystem is destroyed, regardless of its magnitude, its services could be replaced by equivalent ones produced by manmade devices. A rigorous description of how these conditions could allow for a (quasi-)perpetual economic growth was offered in [4] .
The lack of realism of the ecological model behind these analytical schemes was first made clear by Georgescu-Roegen in his “entropic” criticism of economic theory [5] . As further elaborated by Daly and other ecological economists and ecologists1, not only were the full implications of the Entropy Law to the economic process ignored, but in fact the very existence of critical ecosystem services2. Such services emanate from complex and interrelated ecosystems, being exceedingly difficult to replace by capital, and their depletion trajectories follow unforeseeable non-linear patterns due to the ecosystems’ property of resilience. The economic consequence of violating critical resilience thresholds is a sudden decrease in markets’ own ability to allocate mitigation efforts, thus opening the possibility of irreversible feedback mechanisms.
We derive in this paper the theoretical implications of a realistic model for the natural impacts of the economic process. We incorporate elementary facts from Physics and Environmental Science into Baumol's orthodox perspective, which offers rigorous conditions for (quasi-)perpetual usage of resources and seems to allow indefinite economic growth, even under the Entropy Law. Surprisingly, when considering Baumol’s model for resource depletion across all production processes in the economy, under the constraint of critical ecosystem service stocks, we reach in fact the opposite conclusion. We establish the thermodynamic impossibility of indefinite growth in mass-energy scale of the economy free from the risk of catastrophic environmental effects―an assumption commonly made, implicitly or explicitly, by most current growth models. We introduce instead the concept of responsible trajectory, which offers a quantitative criterion for sustainable economic policy.
In view of the inherent uncertainty around critical resilience thresholds, we prove that, even admitting the possibility of science fictional substitutions of capital for natural assets, it is currently irresponsible to enforce, or indeed to maintain, a trajectory of material economic growth.
We are well aware that the impossibility of perpetual growth has long been a consensus in the ecological economics discourse. Our main contribution, therefore, is not the conclusion itself but its derivation from entirely orthodox premises, without resorting to any field-specific category or principle beyond the trivial concept of critical ecosystem service. As a result, it can no longer be dismissed as external to orthodox theory.
Note on the use of Mathematics: while our argument is quantitative, all claims are stated in plain English, keeping mathematical language to a universally accessible minimum and confining technical proofs only to Propositions 6 and 10.
1.1. Initial Definitions and Statement of Main Results
We begin with the following, hopefully uncontroversial, assumption:
Axiom 1. Human economic activity takes place in the physical Universe, hence its process is constrained by the laws of Physics.
Fundamentally, the economic process transforms matter by means of mechanical, chemical and thermal devices which operate within a finite, albeit historically increasing, energy scale. It is therefore convenient to distinguish conceptually the subregion of the Universe where the economic process is a governing phenomenon.
Definition 2. The anthroposphere is the region of the Universe whose current state and dynamics are of the same order of magnitude as the economic process, hence subject to change under human design.
In other words, the anthroposphere is the total material substract of the economic process, together with the underlying interrelations of matter and energy, as imposed by Axiom 1. However, two realms must be distin- guished inside of the anthroposphere: the ecosphere where life exists and the abiotic sphere exogenous to it. Thus the economic process can be understood as the mechanism by which matter-energy exchanges occur within the anthroposphere (Figure 1).
Example 3. (boundaries of the anthroposphere and the ecosphere) The Earth’s atmosphere, land, biodiversity, fossil fuels and minerals, as well as atomic nuclei under interactions controlled by humans, are contained in the anthroposphere. Tidal, tectonic and planetary movements and stellar radiation are not, belonging strictly in the abiotic sphere.
In particular, all the ecosystem services are contained in the ecosphere, and ecosystems are perturbed by the flow of mass-energy from the abiotic sphere. Such exchanges may occur within or without the anthroposphere, i.e., may be respectively the result of human industry or natural phenomena (tectonics, meteorites etc.).
As an immediate consequence of Axiom 1, the anthroposphere as a whole and the economic process in parti- cular are subject to thermodynamic constraints [14] , which we formulate as follows:
Figure 1. Physical universe.
Laws of Thermodynamics. Every transformation process based on mechanical, chemical or thermal devices
or combinations thereof, admits a definite upper bound on efficiency, hence a closed system of such processes has a net negative mass-energy balance with its surroundings, proportional to its scale.
We will give a precise meaning and proof to the following assertion:
Theorem of limited growth. Assuming the Laws of Thermodynamics valid within a neighbourhood of the anthroposphere, one has:
1. The growth in mass-energy scale of the economic process at time 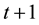 is constrained by the total stock of ecosystem services at time t;
is constrained by the total stock of ecosystem services at time t;
2. Any responsible growth trajectory, as assessed at time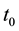 , must predict, within finite and possibly short time
, must predict, within finite and possibly short time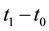 , negative contributions to every type of high-entropy waste emission coming from low-entropy sources external to the ecosphere.
, negative contributions to every type of high-entropy waste emission coming from low-entropy sources external to the ecosphere.
In face of the inherent uncertainty, or perhaps impossibility, in determining the actual critical resilience thresholds for all essential ecosystem services, we arrive at a rather uncomfortable but logically necessary consequence.
Corollary of zero growth. Unless every critical resilience threshold is accurately known for every ecosystem service indispensable to the economic process at a given time, the only responsible nonnegative growth trajec- tory is zero growth.
1.2. Baumol’s Solution to the Depletion Problem
We adopt the definitions from [4] , in mass-energy units, functions of a discrete time variable t (measured e.g. in years):
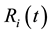 usable stock of resource i on Earth in period t.
usable stock of resource i on Earth in period t.
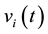 quantity used up during period t.
quantity used up during period t.
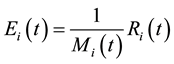 effective stock of resource i in period t, where
effective stock of resource i in period t, where 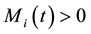 is the inefficiency ratio of the production process w.r.t. resource i.
is the inefficiency ratio of the production process w.r.t. resource i.
Note that recycling within the economy may allow 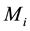 to decrease below 1, i.e., some extracted resources are effectively consumed more than once. The extreme case
to decrease below 1, i.e., some extracted resources are effectively consumed more than once. The extreme case 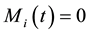 is the regime in which a resource i can be reused indefinitely at zero loss, thus making the effective stock infinite regardless of the actual amount
is the regime in which a resource i can be reused indefinitely at zero loss, thus making the effective stock infinite regardless of the actual amount 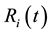 still available.
still available.
Let 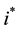 denote the total number of resources involved in the economic process. In those terms, we formulate the relevant corollary of the Laws of Thermodynamics which that author adopts.
denote the total number of resources involved in the economic process. In those terms, we formulate the relevant corollary of the Laws of Thermodynamics which that author adopts.
Claim 4. (thermodynamic bound). For every resource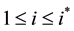 , there is a definite lower bound
, there is a definite lower bound 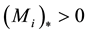 for inefficiency, unsurmountable by innovation.
for inefficiency, unsurmountable by innovation.
Since 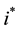 is finite, the overall positive minimum
is finite, the overall positive minimum 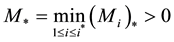 satisfies
satisfies

Baumol proves that, even under the validity of Claim 4, every resource 


That author stops short, however, of considering the aggregate of such trajectories across the whole economy, that is for all resources
2. The Economic Process and the Environment
We wish to quantify the environmental impact of the economic process in terms of its irreversible deposits on the ecosphere, then incorporate this data into Baumol’s model. We define as waste the matter-energy irreme- diably lost to entropy in the form of bound energy states, hence permanently excluded from the production process, according to our formulation of the Laws of Thermodynamics. Since recycled (or recyclable) materials are eventually reintroduced in the productive sphere, they are not considered waste for our purposes. The relevant conceptual framework is illustrated in the following scheme (Figure 2):
Figure 2. Matter-energy in the production process.
Let us begin with the following notation:



The function 



Then, in Baumol’s notation for each resource i and period t, we have:

2.1. Stock of Ecosystem Services
Definition 5. A (critical) ecosystem service is the ecosphere’s capacity (in mass-energy units) to absorb bound states of matter of a given chemical type, or aggregates thereof, without impairing significantly the current economic process.
We need therefore the following additional definitions:




Hence, at time t, we denote the total waste generated from resource i
and the total degradation of ecosystem stock j, due to newly extracted resources,

The fact that not all ecosystem degradation comes from newly extracted resources is expressed by
hence, tautologically,
2.2. Physical Bound on Effective Ecosystem Services
Inefficiency has a lower bound, hence proportional waste is inevitable. We will see that, in such terms, accu- mulated waste eventually exceeds the finite stock of ecosystem services.
Proposition 6. To every increase in the mass-energy scale of the economic process at time t, there corre- sponds an inevitable reduction of some ecosystem stocks, proportional in total to that increase at least, occurring at time
Proof. In the terms of Claim 4 and (2), write 

One obtains trivially from (1) that 

Thus the amount of entropic waste corresponding to every tentative increase in the total mass-energy is not only strictly positive, but indeed at least proportional to the amount of matter-energy entered into the cycle. □
Define the mass-energy scale of the economic process at time t:

Proposition 7. In the absence of external sources of low entropy, there exists a time-independent constant 
Proof. The total mass-energy circulating in the economic process is transformed, by assumption, under mechanical, chemical and thermal interactions, all of which have definite upper-bounds on efficiency, by our physical assumptions. The extensivity property of the entropy function [17] [18] implies that the aggregate of all such processes, considered as a closed system, can operate no more effectively than the most efficient of its constituent processes, hence a definite proportion of the mass-energy in the economic process dissipates unavoidably into the ecosphere, in the form of bound energy states. □
To make that crucial point crystal-clear, if the total amount of matter-energy contained the economic process at time t were still entirely contained in the system at time
2.3. Insufficiency of Markets under Ecological Thresholds
One might argue at this stage that markets’ resourcefulness in face of impending exhaustion of an ecosystem stock would suffice to prevent the actual crossing of the resilience threshold, e.g. by pricing mechanisms which penalise offenders and generate enough incentive towards new alternatives. Unfortunately this objection relies on the fallacy of preemptive knowledge of such thresholds in complex systems.
The fundamental notion here is the epistemological phenomenon of novelty by combination [5] , the fact that composite systems develop qualitative characteristics which are a priori inaccessible even from complete knowledge of its constituent subsystems. For example, it is simply not possible to derive the point at which water transitions from its liquid to gaseous forms by any calculation, using as input some chemical data of the oxygen and hydrogen atoms alone, which eventually returns 100˚C. The boiling point of water is indeed an empirical fact, determined through repeated experimental observation.
Therefore, it is entirely possible that the actual value of an ecosystem stock is beyond assessment by predictive deduction, and can only be quantified empirically, i.e. once it is violated. This means any pricing solution to the use of the remaining stock of such a resource will be essentially anyone’s guess.
Furthermore, such phase transitions might lead to irreversible changes in the environment, towards a new equilibrium state which impairs markets’ very ability to supply equivalent ecosystem services by substituting for, say, additional labour or capital.
Example 8. (definite ecosystem service stock) While ozone gas concentration at the high atmosphere provides useful shielding against stellar radiation, the same ozone at the lower atmosphere interacts strongly with other molecules and is extremely toxic to living systems. The total stock of ozone absorption at the lower atmosphere is a known quantity, beyond which such chemical interactions harm crop production, forest growth and human health [19] .
In the event that our emissions cross the boundary and effects gradually incur, it is indeed possible that the new demand will generate technological and managerial innovations to counter them. However, 1) when taking for granted that deterioration will maintain gradual pace one overlooks the potential feedback effect that our unregulated mitigation efforts might have on further emissions and aggravation of the phenomenon; and in any case, crucially; 2) it remains to consider whether significant progress can be reached at a higher rate than e.g. the increased healthcare costs and agricultural losses degrade our productive capacities.
The above example, which is far from exceptional, illustrates how the exhaustion of an ecosystem stock, at time t, can henceforth hinder the economic process’ normal allocation functions, as assessed at time

3. Low-Entropy Trajectories versus Irresponsible Growth
We formulate a precise quantitative meaning for the responsibility of economic trajectories and prove the Theorem of limited growth. In these terms, any responsible growth in the material scale of the economy must be authorised by actual achievements in innovation which increase the effective stock of ecosystem services. Bringing in the uncertainty of resilience thresholds, we deduce the Corollary of zero growth.
Responsible and Irresponsible Trajectories
Recall from (3) that 
Definition 9. A time-trajectory of the economic process will be deemed responsible at time 
A trajectory is irresponsible at 
A responsible trajectory degrades every ecosystem service j, at every




Proposition 10. Along any responsible trajectory, 
Proof. Taking the infinitesimal form of the mass-energy scale (5) we have:
Set, for clarity,

If, by contradiction, there exists a sequence 



Therefore 
Together with Proposition 6, this proves the Theorem of limited growth.
Finally, since the condition for responsibility [see Definition 9] requires the knowledge at time t of all the quantities
4. Conclusions
Although there is no physically meaningful way to avoid the ultimate consequences of Proposition 10, a few back doors can be proposed. First, a rather pedantic but logically sound point is the fact that the economy can indeed grow perpetually in ways which do not imply a significant increase in matter-energy scale, e.g. by the production of knowledge, culture and art. In any case, this excludes long-term consumerist ambitions, and such path will likely imply an even more revolutionary change in the way which we understand Economics than the alternatives to follow.
Second, and most important, it would be possible to raise the upper bound on the mass-energy scale if the economic process could access sources of low entropy exterior to the ecosphere, hence genuinely recycled bound energy states from the environment (or disposed of them very far away) and restored the net stocks of ecosystem services. Mathematically, this would correspond to a negative term on the right-hand side in Propo- sition 7, thus in principle allowing responsible trajectories with indefinitely increasing effective mass-energy scales.
Such technological solutions, however, remain in the realm of science fiction. If engineers of the future do make the necessary advances, in the form of low-entropy sinks operational at the magnitudes of global production, then the authors of this paper―or rather our descendants―will gladly see our conclusions obsolete, in the eyes of the economists and the public of that future. Meanwhile, to leverage present consumption on the prospective development of futuristic solutions is morally tantamount to a North-American economist, say, gambling their family’s education savings in the derivatives market―which hardly any one would do, regardless of their ideological inclinations.
In face of our current irresponsible trajectory, thermodynamics raises a persuasive warning. Foreseeable outcomes of a collapse of the economic process include worldwide destitution and conflict; the very scenarios envisioned by those who see in perpetual growth the only way to keep social peace.
Acknowledgements
Authors thank Dr. Joeri Rogelj from the Institute for Atmospheric and Climate Science at ETH Zurich for his comments on the draft version.
Cite this paper
Henrique N. SáEarp,Ademar R.Romeiro, (2015) The Entropy Law and the Impossibility of Perpetual Economic Growth. Open Journal of Applied Sciences,05,641-650. doi: 10.4236/ojapps.2015.510063
References
- 1. Hotelling, H. (1931) The Economics of Exhaustible Resources. Journal of Political Economy, 39, 137-175. http://dx.doi.org/10.1086/254195
- 2. Solow, R.M. (1974) The Economics of Resources or the Resources of Economics. American Economic Review, 64.
- 3. Pigou, A.C. (1920) Economics of Welfare. Macmillan Co., London.
- 4. Baumol, W.J. (1986) On the Possibility of Continuing Expansion of Finite Resources. Kyklos, 39, 167-179. http://dx.doi.org/10.1111/j.1467-6435.1986.tb00766.x
- 5. Georgescu-Roegen, N. (1971) The Entropy Law and the Economic Process. Harvard University Press, Cambridge. http://dx.doi.org/10.4159/harvard.9780674281653
- 6. Costanza, R. and Daly, H.E. (1992) Natural Capital and Sustainable Development. Conservation Biology, 6, 37-46. http://dx.doi.org/10.1046/j.1523-1739.1992.610037.x
- 7. Daily, G.C. (1997) Nature Services: Societal Dependence on Natural Ecosystem. Island Press, Washington DC.
- 8. Daly, H.E. (1996) Beyond Growth, The Economics of Sustainable Development. Beacon Press, Boston.
- 9. (2005) Ecosystem and Human Well-Being: Synthesis (Millennium Ecosystem Assessment Series). Island Press, Washington DC.
- 10. Rockström, J., et al. (2009) Planetary Boundaries: Exploring the Safe Operating Space for Humanity. Ecology and Society, 14.
- 11. Rockström, J., et al. (2009) A Safe Operating Space for Humanity. Nature, 461, 472-475. http://dx.doi.org/10.1038/461472a
- 12. Sukhdev, P. (2008) The Economics of Ecosystems and Biodiversity, Interim Report of the Convention on Biological Diversity. European Communities, Cambridge, UK.
- 13. Adaman, F., Devine, P. and Ozkaynak, B. (2012) The Identity of Ecological Economics: Retrospects and Prospects. Cambridge Journal of Economics, 36, 1123-1142. http://dx.doi.org/10.1093/cje/bes021
- 14. Kittel, C. and Kroemer, H. (1980) Thermal Physics. W. H. Freeman Co.
- 15. Ciriacy-Wantrup, S.V. (1952) Resource Conservation: Economics and Policies. University of California Press, Berkerley.
- 16. Bishop, R.C. (1976) Economics of Endangered Species. American Journal of Agricultural Economics, 60.
- 17. Lieb, E.H. and Yngvason, J. (1998) A Guide to Entropy and the Second Law of Thermodynamics. Notices of the American Mathematical Society, 45. http://dx.doi.org/10.1007/978-3-662-10018-9_19
- 18. Lieb, E.H. and Yngvason, J. (1999) The Physics and Mathematics of the Second Law of Thermodynamics. Physics Reports, 310, 1-96. http://dx.doi.org/10.1016/S0370-1573(98)00082-9
- 19. (1999) Scientific Assessment of Ozone Depletion: 1998. WMO Global Ozone Research and Monitoring Project Report, Number 44, World Meteorological Organization/United Nations Environment Programme, Geneva. Introduction to Frequently Asked Questions.
NOTES
1See [6] -[9] [10] -[12] . See also [13] for a survey of the different ecological economics approaches.
2To be fair, not all in the mainstream camp shared such unrealistic views on Nature. Bishop, based on the work of Ciriacy-Wantrup [15] , proposed a SMS (safe minimum standards) approach to handle the risk of irreversible losses of critical ecosystems [16] .















