Open Journal of Applied Sciences
Vol.05 No.08(2015), Article ID:59239,7 pages
10.4236/ojapps.2015.58049
The Numerical Simulation of Aerodynamic Noise Generated by CRH3 Train’s Head Surface
Fanguo Kong, Jian Wang
School of Mechanical and Electrical Engineering, Wuyi University, Jiangmen, China
Email: fgkong@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 August 2015; accepted 25 August 2015; published 28 August 2015
ABSTRACT
In order to solve the increasingly serious problem of railway noise which caused by the train’s speed-up, especially the problem of the dominant aerodynamic noise of the high-speed train, it’s necessary to have a numerical simulation analysis for the CRH3 train’s three dimensional flow model. Setting monitoring points in the positions that the surface curvature changes significantly, using the Large Eddy Simulation Method (LES) to have a transient simulation for the CRH3 train which is in the speed of 300 km/h and 350 km/h, applying the acoustics theory of Lighthill-Curle to predict the aerodynamic noise caused by the head of the CRH3 train. The generation and distribution of the train’s aerodynamic noise are analyzed, so as to provide some reasonable suggestions for the design of the train body.
Keywords:
Aerodynamic Noise, Three Dimensional Flow Mode, Monitoring Points, Large Eddy Simulation (LES), Lighthill-Curle

1. Introduction
At present, domestic and foreign research on the aerodynamic noise of the high-speed train has some achievements: applying the method of large eddy simulation combined with boundary element method, T. Sassa analyzed the distribution of dipole noise sources on the surface of the high speed train body [1] ; through the use of low noise wind tunnel, the relevant personnel studied the air noise existing in the steering frame, train gap, skirt and other position of the high speed train, also, according to some relevant experimental analysis, they got the conclusion that the aerodynamic noise was caused by the pulsating pressure and presented some effective schemes to reduce the aerodynamic noise [2] .
According to the research and experiment of the railway noise theory, the railway noise is mainly composed of three parts: traction noise, wheel rail noise and aerodynamic noise [3] . At present, by means of the damping treatment or dynamic suction of the rail and the wheel, significant achievements have been made in reducing wheel/rail noise. And on the basis of acoustic train conversion speed, after effective control in the wheel rail noise, if the train speed reaches 250 km/h, the aerodynamic noise will become the main part of the railway noise.
This paper is based on Lighthill-Curle theory, using large eddy simulation (LES) method to have a numerical simulation for the CRH3 train’s three dimensional flow model. Thus, the aerodynamic noise caused by the head of the CRH3 train is predicted, and the generation and distribution of the train’s aerodynamic noise are analyzed, so as to provide some reasonable suggestions for the design of the train body.
2. The Numerical Simulation Method of Aerodynamic Noise
2.1. The Large Eddy Simulation (LES) Control Equations
Putting the Navier-Stokes equation in the wave number space or physical space to filter out the vortex which is lower than the limiting width. Thus, we can get the incompressible LES control equation [4] :
 (1)
(1)
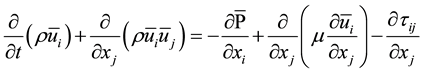 (2)
(2)
Type: (−) is spatial filtering; P is the density;
 and
and
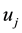 respectively for the filtering of the velocity components; μ is viscosity coefficient; t is time;
respectively for the filtering of the velocity components; μ is viscosity coefficient; t is time;
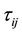 is the subgrid scale stress
is the subgrid scale stress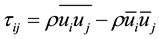 .
.
2.2. The Aerodynamic Noise Control Equation
Based on N-S equation and continuity equation, Lighthill derived the acoustic propagation equation [5] :
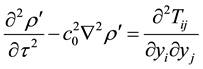 (3)
(3)
Type:
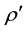 for the density of fluctuations,
for the density of fluctuations,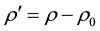 ;
;
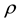 and
and
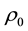 is respectively the density of the disturbance and the disturbance; Lighthill tensor
is respectively the density of the disturbance and the disturbance; Lighthill tensor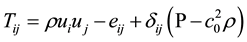 ;
;
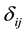 is Delta Kronecker symbol; Viscous stress tensor
is Delta Kronecker symbol; Viscous stress tensor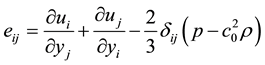 ;
;
 is Sound velocity;
is Sound velocity;
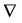 is Hamilton operator.
is Hamilton operator.
When the solid wall boundary exists in the unsteady flow region, the solution of the Equation (3) is derived [6] :

Type:





Type (4) contains two kinds of noise sources:
1) One kind of noise sources is the surface dipole term of Lighthill stress which is in the flow field around the object, and the dipole source noise is proportional to the three Party of the Maher number.
2) The other kind of noise sources is the sub volume quadrupole between the surface pressure and the viscous shear stresses, and the quadrupole source noise is proportional to the five Party of Maher number.
So, the noise of the quadrupole source is proportional to the square of the Maher number.
The speed of high speed train is 300 km/h and 350 km/h, the Maher number are 0.24 and 0.28 respectively. Since the noise of the quadrupole source is relatively small, it can be neglected. Therefore, the formula for the aerodynamic noise of high speed train is:


Type:



3. The Basic Link of Aerodynamic Noise Numerical Calculation
3.1. The Numerical Calculation of Train Model
It is hard for computer to achieve the large eddy simulation calculation on the whole vehicle model [7] . Since the middle cross section of the train is roughly the same, after the air flows a certain distance from the train head, the structure of the flow boundary layer tends to be stable. Meanwhile, the change of the aerodynamic force of the train tends to be stable.
On the basis of the above analysis, selecting the 2 compartment models which are the head carriage and rear carriage. Taking into account that the influence of the wiper position on the front of the aerodynamic noise, the geometric model preserving the structural features of wiper, as shown in Figure 1.
3.2. The Numerical Calculation Region
When calculate in the numerical simulation, In order to avoid the influence of the exit section of the EMU, the selection of the length direction size should make sure that the calculation of the area downstream from the train tail [8] .
The CRH3 train length l = 41.4 m, height h = 3.89 m, width w = 3.3 m, the entrance length of the calculation region l1 = 70 m > l and export length l2 = 130 m » 3l. The height of calculation region H = 80 m > 20 h, width W = 120 m, as shown in Figure 2.
Figure 1. The calculation model of CRH3.
Figure 2. The calculation area.
3.3. The Grid of the Numerical Calculation Model
Complex structures such as the windshield wipers on the train’s head, the surface shape of the CRH3 train’s head is irregular. This paper apply unstructured tetrahedral grid to mesh the train body. After mesh, the grid near the train position is more intensive than other position, and the grid transit uniformly from the train body to external area with certain growth factors that vary from dense to sparse. The minimum grid size is 0.004 m, the minimum grid area reaches

3.4. The Set of Boundary Conditions
For the speed of the train is not less than 300 km/h, there are two kinds of method can be used to calculate. One is direct transient calculation, the other is transient calculation based on the steady result as the initial value. At the same time step, using the first method to calculate will cost double computation time than the second method. Considering the above considerations, it is better to take the method that transient calculation based on the steady result as the initial value. Thus, the boundary conditions are shown in Table 1.
4. The Fluctuating Pressure Simulation of the Head Surface
When the speed of CRH3 is 350 km/h, the pressure distribution of the front surface is obtained, as shown in Figure 4(a); when the speed of CRH3 is 300 km/h, the pressure distribution of the front surface is obtained, as shown in Figure 4(b).
4.1. The Result of the Fluctuating Pressure Simulation
Airflow is easy to exist separation phenomenon in the position that surface curvature changes highlighted, and the formation of flow disturbances will become very complex. So the monitoring points should set in the position that surface curvature is more prominent, such as shown in Figure 5.
The CRH3 train are respectively traveling at the speed of 300 km/h and 350 km/h, through the simulation, it can be learned that the relationship between the fluctuation pressure of each monitoring point at different speeds and the traveling time ,which is shown in Figure 6.
Respectively record the fluctuation range and the fluctuation amplitude of the front surface pressure when the CRH3 train at the speed of the 300 km/h and 350 km/h, as shown in Table 2.
According to the pressure of the train head surface, following conclusions can be drawn:
1) Since the surface curvature change of the monitoring points 1 and 2 are bigger, the fluctuation pressure and the fluctuation range of these two positions are relatively larger.
Figure 3. The grid of longitudinal section.
Table 1. Boundary conditions setting.


Figure 4. The front surface pressure distribution. (a) 350 km/h; (b) 300 km/h.
Table 2. The time fluctuating pressure of monitoring points.
Figure 5. The front surface monitoring points setting.

Figure 6. The time fluctuating pressure of some monitoring points. (a) 350 km/h; (b) 300 km/h.
2) The disturbance degree of the train on the air flow field is changing with the train speed, the greater speed, the greater fluctuation amplitude of fluctuating pressure.
3) When the velocity are respectively 300 km/h and 350 km/h, the maximum value of the pressure fluctuation is corresponding to






To sum up, the greater the change of curvature of the front surface, the greater the flow disturbance, corresponding the larger the pressure fluctuation and the fluctuation range amplitude; the amplitude of fluctuating pressure and the second party of the running speed approximately have a direct proportional relationship.
4.2. The Spectral Analysis of the Pulse Pressure of the Front Surface
In the case that the Maher number is low, the main noise source is the dipole. Since the running speed of the train is different, it’s essential to change the fluctuation pressure of monitoring points into Sound pressure level spectrum by Fast Fourier Transform (FFT), as shown in Figure 7.
Using the total sound pressure formula, when there are large numbers of sound pressure lever, the overall sound pressure level is

at different frequencies, it is needed to have a calculation of the total pulsational sound pressure value of each monitoring point, as shown in Table 3.

Figure 7. The spectrum of some monitoring points. (a) 350 km/h; (b) 300 km/h.
Table 3. The total sound pressure level of monitoring points.
According to the spectral analysis from the FFT conversion of the pulse pressure, the following conclusions can be drawn:
1) On the surface of the train head, the air flow is easy to be separated, and the turbulent motion area is easy to cause the aerodynamic noise. The frequency band of the aerodynamic noise is wider, and the dominant frequency is not obvious;
2) With the increase of the running speed of the train, the aerodynamic noise at every level frequency changes more dramatic, and the distribution of the spectrum is more fine;
3) In the low frequency region, the acoustic pressure level and the sound pressure level density of the monitoring points are higher; in the low frequency region, the acoustic pressure level and the sound pressure level density of the monitoring points are lower. Therefore, the energy of the aerodynamic noise in the low frequency part is relatively large, however, in the high frequency part is small.
5. Conclusions
This paper is based on Lighthill-Curle theory, using large eddy simulation (LES) method to have a numerical simulation for the CRH3 train’s three dimensional flow model. Thus, the aerodynamic noise caused by the head of the CRH3 train is predicted, and the generation and distribution of the train’s aerodynamic noise are analyzed. The results show that:
1) With the increase of train speed, the fluctuating pressure amplitude and speed of every point on the front surface will be increased, and the pressure fluctuation spectrum is finer;
2) The frequency band of the pulse pressure is very wide, and has no obvious dominant frequency. At low frequencies, the amplitude of the pulse pressure is large; at high frequencies, the amplitude of the pulse pressure is decreased with the negative exponential law;
3) The energy of the aerodynamic noise in the low frequency part is relatively large, however, in the high frequency part is small.
In order to effectively decrease the aerodynamic noise of the high speed train, it is viable to minimize the concave convex surface which should be replaced with the streamlined smooth transition surface for the body design.
Acknowledgements
The work was supported by grant No.06029824 of the National Science Foundation Program of Guangdong province of China.
Cite this paper
FanguoKong,JianWang, (2015) The Numerical Simulation of Aerodynamic Noise Generated by CRH3 Train’s Head Surface. Open Journal of Applied Sciences,05,501-508. doi: 10.4236/ojapps.2015.58049
References
- 1. Sassa, T., Sato, T. and Yatsui, S. (2001) Numerical Analysis of Aerodynamic Noise Radiation from a High-Speed Train Surface. Journal of Sound and Vibration, 247, 407-416.
http://dx.doi.org/10.1006/jsvi.2001.3773 - 2. Holmes, B. and Dias, J. (1997) Predicting the Wind Noise from the Pantograph Cover of a Train. International Journal for Numerical Methods in Fluids, 24, 1307-1319.
http://dx.doi.org/10.1002/(SICI)1097-0363(199706)24:12<1307::AID-FLD561>3.0.CO;2-8 - 3. Keda, M., Suzuki, M. and Yoshida, K. (2006) Study on Optimization of Panhead Shape Possessing Low Noise and Stable Aerodynamic Characteristics. Quarterly Report of Railway Technical Research Institute, 47, 72-77.
- 4. Iwamoto, K. and Higashi, A. (1993) Some Consideration toward Reducing Aerodynamic Noise on Pantograph. Japanese Railway Engineering, 122, 1-4.
- 5. Peng L.J. and Shen Y.G. (2011) Numerical Analysis of Fluctuating Pressure of High Speed Vehicle. Machinery Design and Manufacture, 10, 176-178.
- 6. Kitagawa, T. and Nagakura, K. (2000) Aerodynamic Noise Generated by Shinkansen Cars. Journal of Sound and Vibration, 231, 913-924. http://dx.doi.org/10.1006/jsvi.1999.2639
- 7. Fremion, N., Vincent, N. and Jacob, M. (2000) Aerodynamic Noise Radiated by the Intercoach Spacing and the Bogie of a High-Speed Train. Journal of Sound and Vibration, 231, 577-593.
http://dx.doi.org/10.1006/jsvi.1999.2546 - 8. Huang, Y.Y. (2012) Numerical Simulation of Aerodynamic Noise for EMU. Master Thesis, Dalian Jiaotong University, Dalian.
- 9. Xiao, Y.G. and Kang, Z.C. (2008) Numerical Prediction of Aerodynamic Noise Radiated from High Speed Train Head Surface. Journal of Central South University (Science and Technology), 39, 1267-1272.







