Open Journal of Applied Sciences
Vol.3 No.1(2013), Article ID:29447,6 pages DOI:10.4236/ojapps.2013.31009
An Optimal Control Problem for Hypoxemic Hypoxia Tissue-Blood Carbon Dioxide Exchange during Physical Activity
1National University of Rwanda, Butare, Rwanda
2Department of Mathematics and Computer Science, Dakar University, Dakar, Senegal
Email: *jmnta@yahoo.fr,
Received November 2, 2012; revised December 3, 2012; accepted December 10, 2012
Keywords: Arterial Oxygen Pressure; Arterial Dioxide Pressure; Cardiovascular/Respiratory System; Optimal Control Problem; Numerical Simulation
ABSTRACT
This paper aims at solving an optimal control problem for determining the response of hypoxia to heart rate and alveolar ventilation that are cardiovascular and respiratory control respectively during a physical activity. A two nonlinear coupled ordinary differential equations is presented. The cost function of optimal control problem is discretized using the linear B-splines functions defined on a regular grid. The results show the determinant parameters stabilized at normal value.
1. Introduction
Hypoxia, or hypoxiation, is defined as a pathological condition related to adequate oxygen supply in human body. It is in two main types: the generalized hypoxia that is characterized by the deprived adequate oxygen supply in whole body and tissue hypoxia which happens in its region. It differs from hypoxemia called also hypoxaemia in that within the arterial blood the oxygen concentration is abnormally low. Hypoxemia was originally defined as a deficiency of oxygen in arterial blood but standard manuals take this to mean an abnormally low partial pressure of oxygen, content of oxygen or percent saturation of hemoglobin with oxygen, either found singly or in combination. The serious cases of the hypoxemia happen when the decreased partial pressure of oxygen in blood is less than 60 mmHg.
In addition, the generalized hypoxia occurs in healthy people when they ascend to high altitude, where it causes altitude sickness leading to point constitutes the beginning of the steep portion of the hemoglobin dissociation curve, where a small decrease in the partial pressure of oxygen results in a large decrease in the oxygen content of the blood or when hemoglobin oxygen saturation is less than 90%. The reason of this is this potentially fatal complications including high altitude pulmonary edema (HAPE) and high altitude cerebral edema (HACE) [1]. It also occurs in healthy individuals when breathing mixtures of gases with low oxygen content.
Hypoxic hypoxia is a result of insufficient oxygen available to the lungs. The examples of how lungs can be deprived of oxygen are a blocked airway, a drowning or a reduction in partial pressure (high altitude above 10,000 feet). Hypoxia is also a serious consequence of pre-term birth in the neonate.
The main cause for this is that the lungs of the human fetus are among the last organs to develop during pregnancy.
To assist the lungs to distribute oxygenated blood throughout the body, infants at risk of hypoxia are often placed inside an incubator capable of providing continuous positive airway pressure (also known as a humidicrib). The insufficient delivery of oxygen (low ) or inability to utilize oxygen (normal
) or inability to utilize oxygen (normal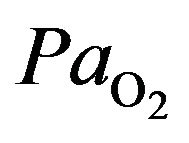 ) causes also the hypoxia where we assist to oxygen deficiency at the mitochondrial sites. This phenomeno accurs when
) causes also the hypoxia where we assist to oxygen deficiency at the mitochondrial sites. This phenomeno accurs when 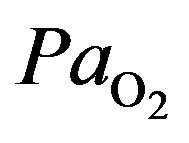 less than 7.3 kPa (55 mmHg). Below this threshold the ventilation starts to stimulate carotid body activity. The hyperventilation reduces
less than 7.3 kPa (55 mmHg). Below this threshold the ventilation starts to stimulate carotid body activity. The hyperventilation reduces 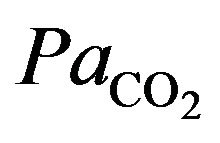 and
and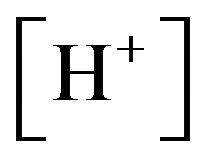 , which limits the initial rise in ventilation, because it decreases the carotid body and central chemoreceptor stimuli. In fact, in humans, hypoxia is detected by chemoreceptors in the carotid body. This response does not control ventilation rate at normal
, which limits the initial rise in ventilation, because it decreases the carotid body and central chemoreceptor stimuli. In fact, in humans, hypoxia is detected by chemoreceptors in the carotid body. This response does not control ventilation rate at normal , but below normal the activity of neurons innervating these receptors increases dramatically, so much so to override the signals from central chemoreceptors in the hypothalamus, increasing
, but below normal the activity of neurons innervating these receptors increases dramatically, so much so to override the signals from central chemoreceptors in the hypothalamus, increasing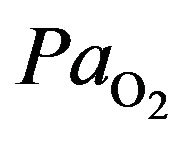 despite a falling
despite a falling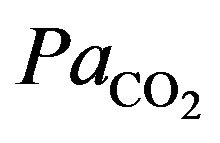 .
.
Any physical activity obviously causes the body to demand more oxygen for normal functioning. The muscles rob the brain of the marginal amounts of oxygen available in the blood and the time of onset of hypoxic symptoms is shortened. However, the improvement of performance of athlete in high altitude results in a mild and non-damaging intermittent hypoxia used intentionally during training to develop an athletic performance adaptation at both the systemic and cellular level. Mathematical models quantifying hypoxic hypoxia have been proposed [2-4]. The optimal control problem based on the responses of cardiovascular respiratory system parameters to its controls, heart rate and alveolar ventilation, during physical activity has not been considered in the situation of hypoxic hypoxia. This work focuses on this issue where the mathematical model is modified to include the controls of cardiovascular respiratory system.
The remainder of this paper is structured as follows. In Section 2, we present a mathematical model, an optimal control problem and its descretization. The results of numerical simulation are discussed in Section 3. In Section 4 deals with concluding remarks.
2. Setting of an Optimal Control Problem
The model we present in this paper involves modifying of model equations as developed by Guillermo Gutierrez [2] in order to include the role of physical activity. The diagram for a two compartmental model is illustrated in the Figure 1 where mass transport model of tissue CO2 exchange is developed to examine the relative contributions of blood flow and cellular hypoxia (dysoxia) to increases in tissue and venous blood CO2 concentration.

Figure 1. Diagram for the tissue carbon dioxide (CO2) exchange model where [CO2] represents the total CO2 concentration (dissolved and bound) and the subscripts t and v denote the tissue and vascular compartments respectively. Kv is the mass transfer coefficient for CO2. For the vascular compartment, the rate of change of [CO2] v depends on blood flow per unit volume of tissue 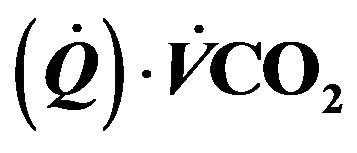 denotes carbon dioxide production.
denotes carbon dioxide production.
From this compartmental diagram the model equations are as follows.
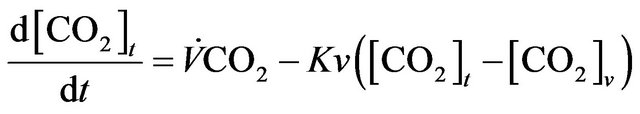 (1)
(1)
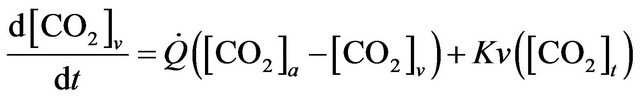 (2)
(2)
The integral role of physical activity results in the influence of the demand of the tissues for oxygen during hypoxia in altitude. Just as resting ventilation increases dramatically at high altitude, so does ventilation during physical activity. In fact, at moderate levels of physical activity, there is little or no change in arterial 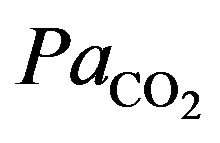 between rest and exercise. Since carbon dioxide production for a given work level is essentially independent of altitude, this means that measured ventilation is independent of altitude at a given work level. At work levels approaching maximal values at any altitude, alveolar and arterial
between rest and exercise. Since carbon dioxide production for a given work level is essentially independent of altitude, this means that measured ventilation is independent of altitude at a given work level. At work levels approaching maximal values at any altitude, alveolar and arterial  fall compared with the resting level and physical activity ventilation measured at correspondingly rises. Furthermore, during exercise, increases in alveolar ventilation must parallel the increased tissue oxygen consumption and carbon dioxide production by the exercising muscles, both of which rise in direct proportion to the increase in power output. These relationships are governed by the following equation
fall compared with the resting level and physical activity ventilation measured at correspondingly rises. Furthermore, during exercise, increases in alveolar ventilation must parallel the increased tissue oxygen consumption and carbon dioxide production by the exercising muscles, both of which rise in direct proportion to the increase in power output. These relationships are governed by the following equation
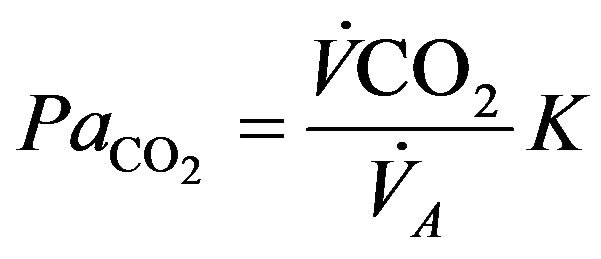
where 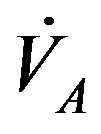 is alveolar ventilation and
is alveolar ventilation and 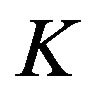 denotes a constant [5], so that we have
denotes a constant [5], so that we have

where 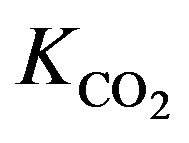 the slope of the physiological
the slope of the physiological 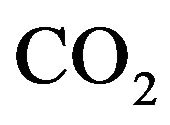 dissociation curve and
dissociation curve and 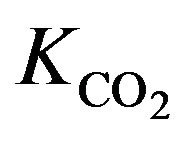 constant for the physiological
constant for the physiological 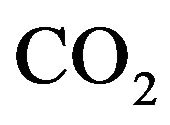 dissociation curve [6].
dissociation curve [6].
Taking RQ as respiratory exchange ration and  as consummation rate of O2, the relationship between
as consummation rate of O2, the relationship between 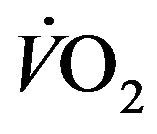 and
and 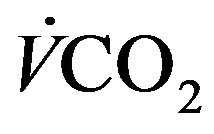 satisfies the following relation [2].
satisfies the following relation [2].
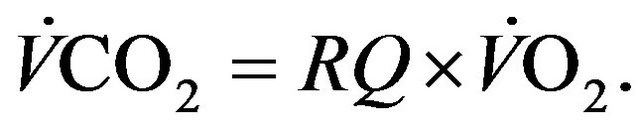 (3)
(3)
Using Fick’s principle [2] applied to the relation (3) allows to get
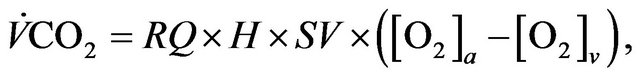
where 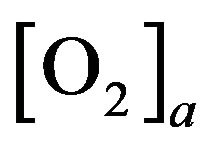 (resp.
(resp.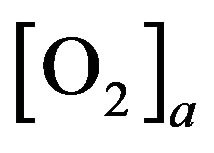 ) is arterial (venous) concentration of
) is arterial (venous) concentration of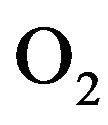 ,
,  denotes heart rate and
denotes heart rate and 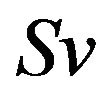 represents stroke volume.
represents stroke volume.
In addition, it is known that the human respiratory control system varies the ventilation rate 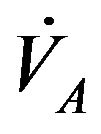 in response to the levels of
in response to the levels of 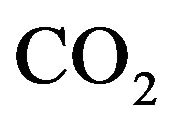 and
and 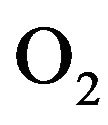 in the body and the control mechanisms of cardiovascular system influences global control in the blood vessels as well as well as heart rate
in the body and the control mechanisms of cardiovascular system influences global control in the blood vessels as well as well as heart rate  for impacting blood flow
for impacting blood flow 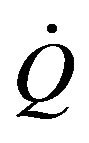 [7]. Generally, during physical activity in altitude and particular in the hypoxia case, the control mechanism of these two systems plays a crucial role.
[7]. Generally, during physical activity in altitude and particular in the hypoxia case, the control mechanism of these two systems plays a crucial role.
Finally, we are interested in the following model equations
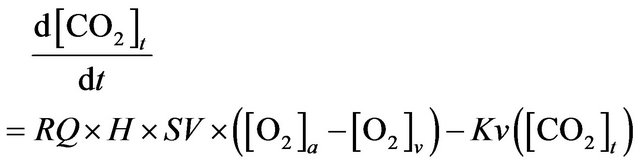 (4)
(4)
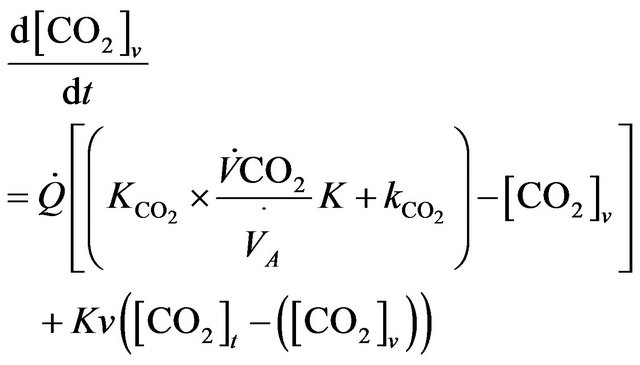 (5)
(5)
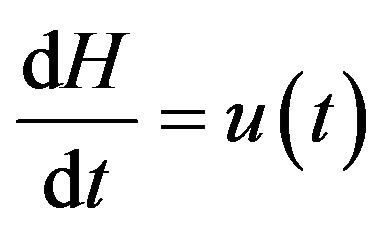 (6)
(6)
 (7)
(7)
where two last ordinary differential equations describe the control of cardiovascular and respiratory system is described respectively with 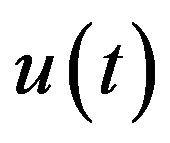 and
and  the functions to be determined by an optimality criterion.
the functions to be determined by an optimality criterion.
The alveolar gas equation allows the calculation of the alveolar partial pressure of oxygen as follows [8]
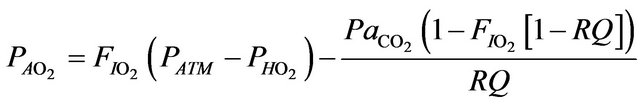
where 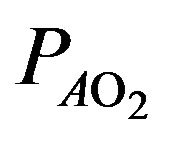 is the alveolar partial pressure of oxygen,
is the alveolar partial pressure of oxygen, 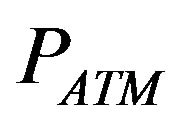 denotes the prevailing atmospheric pressure,
denotes the prevailing atmospheric pressure, 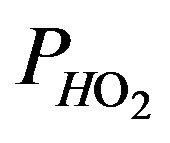 represents the saturated vapor pressure of water at body temperature and the prevailing atmospheric pressure and
represents the saturated vapor pressure of water at body temperature and the prevailing atmospheric pressure and  is the fraction of inspired gas that is oxygen (expressed as a decimal). In addition, the relation between alveolar partial and arterial pressure of oxygen is given by
is the fraction of inspired gas that is oxygen (expressed as a decimal). In addition, the relation between alveolar partial and arterial pressure of oxygen is given by
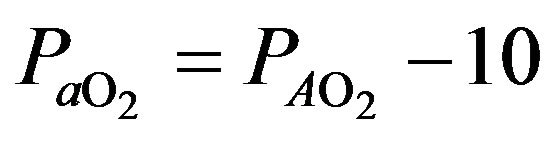
because the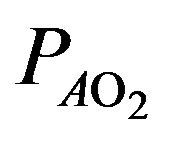 to
to 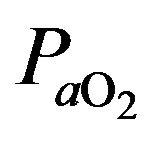 gradient is normally close to and is written as follows:
gradient is normally close to and is written as follows:
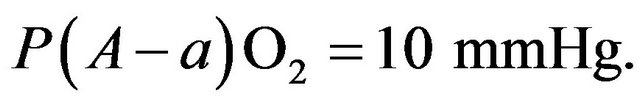
Similarly, blood 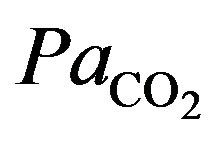 is calculated on the basis of the Henderson-Hasselbach equation [9] as follows.
is calculated on the basis of the Henderson-Hasselbach equation [9] as follows.

where  is
is  content of plasma defined by Douglas [10] as
content of plasma defined by Douglas [10] as
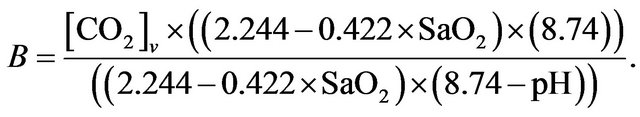
It results that the alveolar carbon dioxide pressure of oxygen 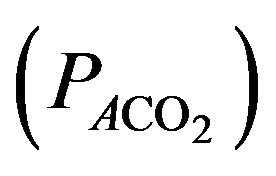 is equivalent to
is equivalent to  (there is no gradient).
(there is no gradient).
Furthermore, it appears that a main goal of respiratory control is to keep 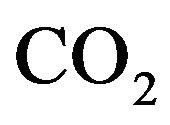 venous partial pressure as close as possible to an equilibrium value denoted by
venous partial pressure as close as possible to an equilibrium value denoted by 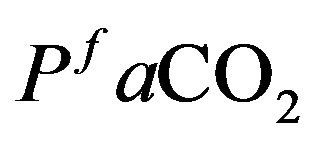 and, to a lesser extent, control
and, to a lesser extent, control 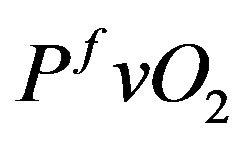 to the equilibrium such that the cost functional can be formulated in the following way.
to the equilibrium such that the cost functional can be formulated in the following way.
Find 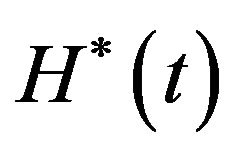 and
and 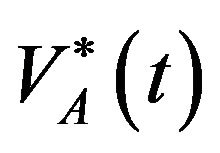 solution of
solution of
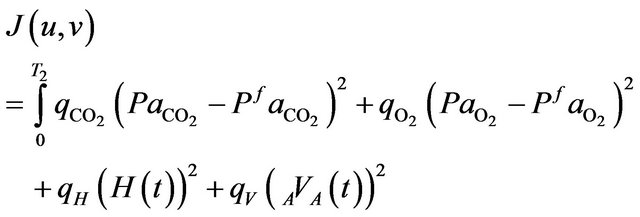 (8)
(8)
subject to the systems (4 )-(7).
In the relation (8), the positive scalar coefficients 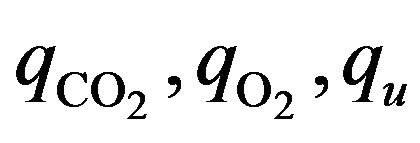 and
and 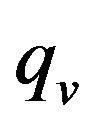 determine how much weight is attached to each cost component term in the integrand while
determine how much weight is attached to each cost component term in the integrand while 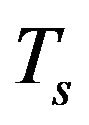 denotes the maximum time that the physical activity can take.
denotes the maximum time that the physical activity can take.
Let us consider 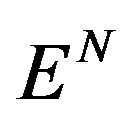 the vector space that is span of
the vector space that is span of
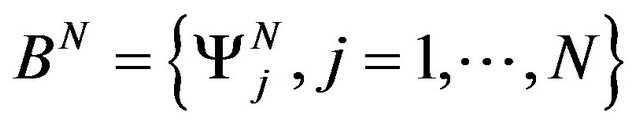 (9)
(9)
a base of linear B-splines functions on a regular grid
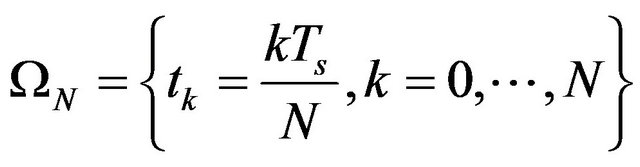 (10)
(10)
The functions 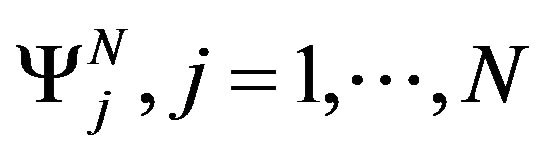 verify the following relation
verify the following relation 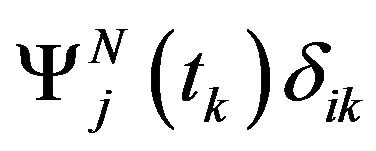 where
where  denotes Kronecker symbol. The descretization of the optimal problem (8) is done by setting the state vector
denotes Kronecker symbol. The descretization of the optimal problem (8) is done by setting the state vector
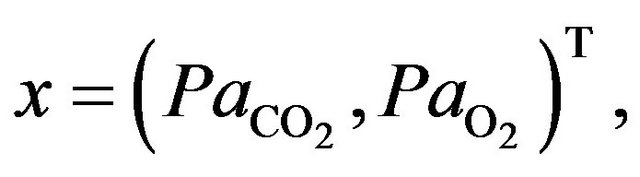
and the desired final vector
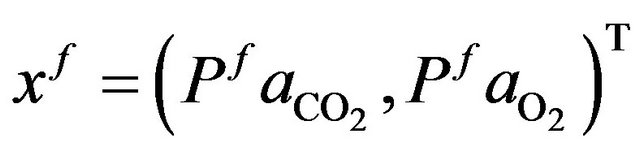
such that it can be written as follows.
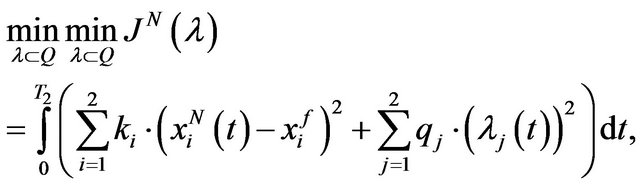 (11)
(11)
where
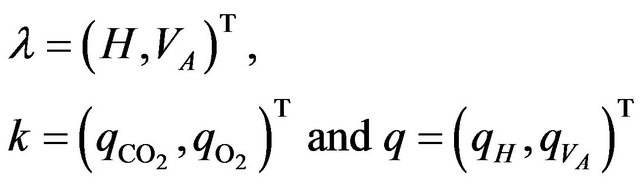
with 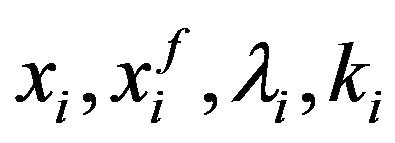 and
and 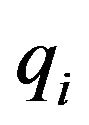 respectively the
respectively the 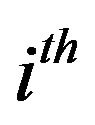 component of the vectors
component of the vectors  and
and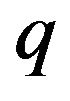 .
.
We are looking for  a approximated solution of (11) in the set
a approximated solution of (11) in the set 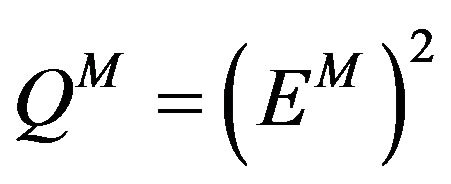 such that
such that
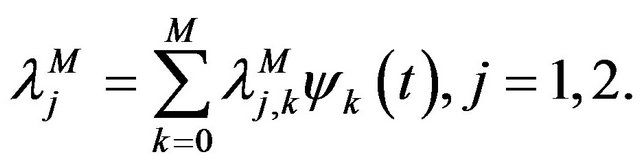 (12)
(12)
Therefore the cost function (11) becomes
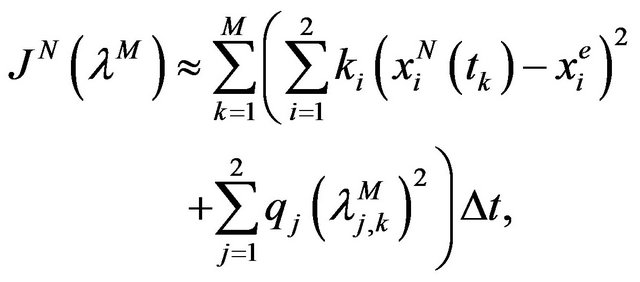 (13)
(13)
with 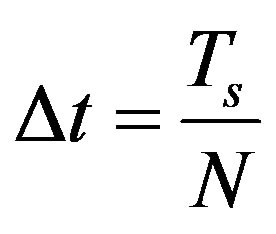 and finally the discrete formulation of optimal problem (8) subject to (4)-(7) is written as follows
and finally the discrete formulation of optimal problem (8) subject to (4)-(7) is written as follows
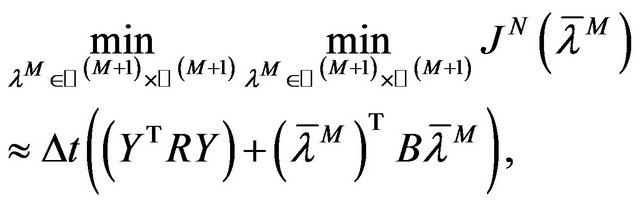 (14)
(14)
where 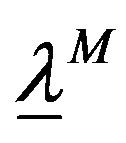 is a matrix
is a matrix  such that the components
such that the components 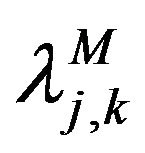 are components of the function
are components of the function 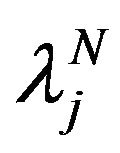 in the set
in the set 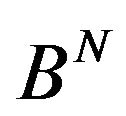 and
and 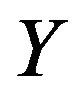 represents the matrix with
represents the matrix with 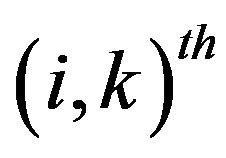 component is
component is

where 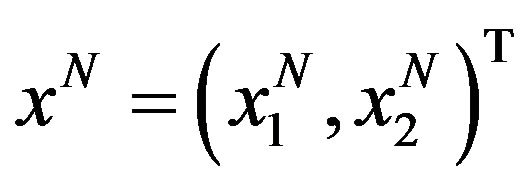 denotes the solution of the systems (4)-(5) associated to
denotes the solution of the systems (4)-(5) associated to ,
,  and
and  are matrix defined by
are matrix defined by
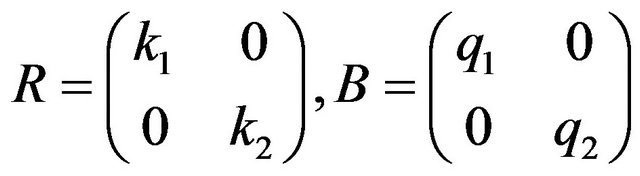 (15)
(15)
3. Test Results
For solving the optimal control problem (13) subject to the constraints (4)-(7) we consider the parameters presented in the Table 1.
We take 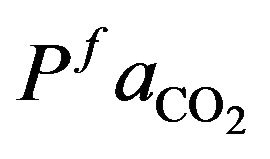 and
and 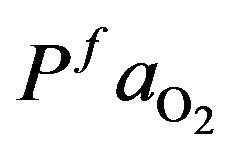 as normal value for a healthy individual that
as normal value for a healthy individual that 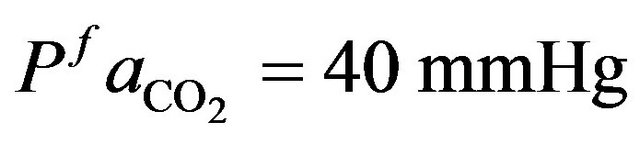 and
and 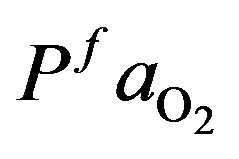
= 95 mmHg. The variation curve of carbon dioxide in the tissues and carbon dioxide in vascular is illustrated in the Figure 2. The control of cardiovascular and respiratory systems,  and
and 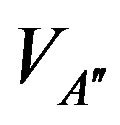 against the time are given in the Figure 3 whereas the Figure 4 shows the responses of these controls.
against the time are given in the Figure 3 whereas the Figure 4 shows the responses of these controls.
Table 1. Values of parameters used in numerical simulation.

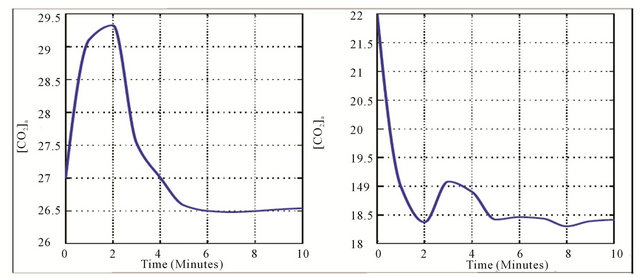
The Figure 2 shows a decrease of arterial and venous dioxide carbon concentration against the time. They are maintained at a level where the variation is small. This is due to the effect of ventilation during physical activity. In fact, ventilation increases abruptly in the initial stages of exercise and is then followed by a more gradual increase. This mechanism of increase results of to motor centre activity and afferent impulses from proprioceptors of the limbs, joints and muscles. Since peripheral chemoreceptors are responsible for increasing ventilation, Central chemoreceptors may be readjusted to increase ventilation to maintain carbon dioxide concentrations.
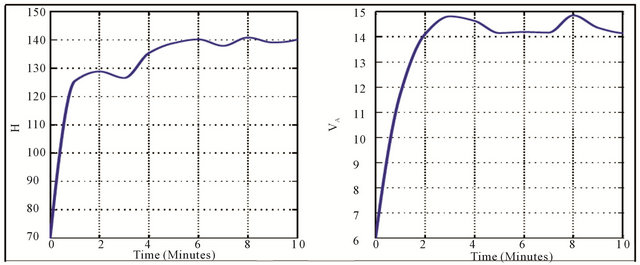
At the onset of physical activity, the heart rate and alveolar ventilation increase. Generally, heart rate increases to about 90% of its maximum values during strenuous physical activity. Furthermore, the ventilation increases with increases in work rate at submaximal physical activity intensities. These physiological effects of physical activity on cardiovascular-respiratory system are justified by the variation of its controls in the Figure 3 where they reach a value and they are stabilized with small oscillations.
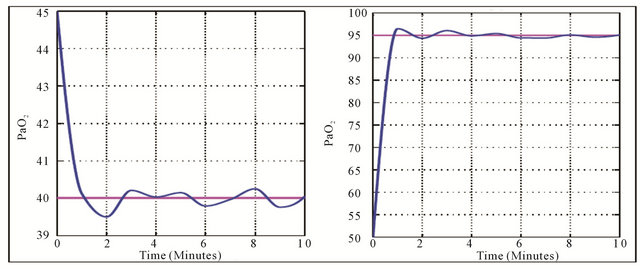
The Figure 4 shows the arterial carbon dioxide (resp. oxygen) decreases (increases) at the onset of physical activity to be stabilized at normal value. The changes which occur in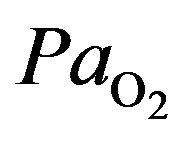 and
and 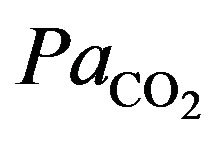 values during exercise are usually small. But since hypoxia is characterized by the adequate oxygen supply deprived in whole (generalized hypoxia) or a region of the body (tissue hypoxia) the ventilation process during physical activity plays an integral role. During physical activity, when sufficient oxygen for flux through the is not available, the increased reliance on glycolysis results in increased accumulation of lactic acid, which initially leads to an increase in
values during exercise are usually small. But since hypoxia is characterized by the adequate oxygen supply deprived in whole (generalized hypoxia) or a region of the body (tissue hypoxia) the ventilation process during physical activity plays an integral role. During physical activity, when sufficient oxygen for flux through the is not available, the increased reliance on glycolysis results in increased accumulation of lactic acid, which initially leads to an increase in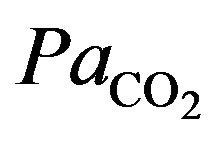 . However, this is counteracted by the stimulation of ventilation and as a result
. However, this is counteracted by the stimulation of ventilation and as a result 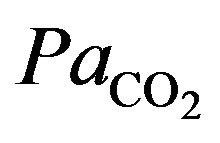 is decreased. In addition, in
is decreased. In addition, in
 (a) (b)
(a) (b)
Figure 2. Variation of arterial (a) and (b) carbon dioxide.
 (a) (b)
(a) (b)
Figure 3. Variation of heart rate (a) and alveolar ventilation (b).
 (a) (b)
(a) (b)
Figure 4. Variation of optimal parameters: Arterial carbon dioxide pressure (a) and arterial oxygen pressure (b).
humans, hypoxia is detected by chemoreceptor in the carotid body. This response does not control ventilation rate at normal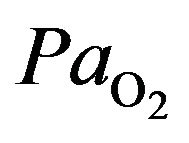 , but below normal the activity of neurons innervating these receptors increases dramatically, so much so to override the signals from central chemoreceptors in the hypothalamus, increasing
, but below normal the activity of neurons innervating these receptors increases dramatically, so much so to override the signals from central chemoreceptors in the hypothalamus, increasing 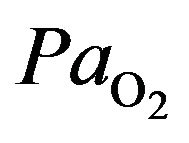 despite a falling
despite a falling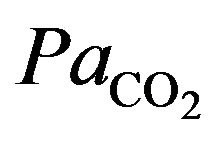 .
.
4. Conclusion
In this work we have investigated a role of controls of cardiovascular-respiratory system during physical activity to hypoxia. The heart rate and both minute ventilation and alveolar ventilation increase; in this way the lungs transfer more oxygen and carbon dioxide and keep pace with metabolic demands. In this increase of the controls result the increase of arterial and vascular carbon dioxide. In addition, the partial arterial pressure of carbon dioxide and oxygen are maintained at normal value.
REFERENCES
- A. Cymerman and P. B. Rock, “Medical Problems in High Mountain Environments,” A Handbook for Medical Officers, USARIEM-TN94-2, US Army Research Institute of Environmental Medicine Thermal and Mountain Medicine Division Technical Report, 2009.
- G. Gutierrez, “A Mathematical Model of Tissue-Blood Carbon Dioxide Exchange during Hypoxia,” American Journal of Respiratory Critical Care Medecine, Vol. 169. No. 4, 2004, pp. 525-533. doi:10.1164/rccm.200305-702OC
- J. J. Tyson and B. Novak, “Regulation of the Eukariotic Cell-Cycle: Molecular Antagonism, Hysteresis, and Irreversible Transitions,” Journal of Theoretical Biology, Vol. 210, No. 2, 2001, pp. 249-263. doi:10.1006/jtbi.2001.2293
- D. Gammack, H. M. Byrne and C. E. Lewis, “Estimating the Selective Advantage of Mutant p53 Tumour Cells to Repeated Rounds of Hypoxia,” Bulletin of Mathematical Biology, Vol. 63, No. 1, 2001, pp. 135-166. doi:10.1006/bulm.2000.0210
- J. A. Dempsey, H. V. Forster and D. M. Ainsworth, “Regulation of Hyperpnea, Hyperventilation, and Respiratory Muscle Recruitment during Exercise,” In: J. A. Dempsey and A. I. Pack, Eds., Regulation of Breathing, Marcel Dekker, New York, 1995, pp. 1065-1133.
- S. Timischl, “A Global Model for the Cardiovascular and Respiratory System,” PhD Thesis, Karl Franzens Universit of Graz, 1998.
- S. Timischl, J. J. Batzel and F. Kappel, “Modeling the Human Cardiovascular Respiratory Control System: An Optimal Control Application to the Transition to NonREM Sleep,” Spezialforschungsbereich F-003 Technical Report 190, Karl Franzens Universitat, 2000.
- D. Curran-Everett, “A Classic Learning Opportunity from Fenn, Rahn, and Otis (1946): The Alveolar Gas Equation,” Advances in Physiology Education, Vol. 30, No. 2, 2006, pp. 58-62. doi:10.1152/advan.00076.2005
- I. Giovannini, C. Chiarla, G. Boldrini and M. Castagneto, “Calculation of Venoarterial CO2 Concentration Difference,” Journal of Applied Physiology, Vol. 74, No. 2, 1993, pp. 959-964.
- A. R. Douglas, N. L Jones and J. W. Reed, “Calculation of Whole Blood CO2 Content,” Journal of Applied Physiology, Vol. 65, No. 1, 1988, pp. 473-477.
NOTES
*Corresponding author.

