Journal of High Energy Physics, Gravitation and Cosmology
Vol.02 No.04(2016), Article ID:70095,15 pages
10.4236/jhepgc.2016.24046
Gedanken Experiment for Looking at dgtt for Initial Expansion of the Universe and Influence on HUP via Dynamical Systems, with Positive Pre-Planckian Acceleration
Andrew Walcott Beckwith
Physics Department, College of Physics, Chongqing University Huxi Campus, Chongqing, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 3, 2016; Accepted: August 22, 2016; Published: August 25, 2016
ABSTRACT
We examine through the lens of dynamical systems a “one dimensional” time mapping of emergent VEV from Pre-Planckian space time conditions. As it is, we will from first principles examine what adding acceleration does as to the HUP previously derived. In doing so, we will be trying it in our discussion with the earlier work done on the HUP. 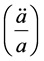 not equal to zero, constant, but large would frequently imply
not equal to zero, constant, but large would frequently imply 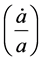 which would have three dissimilar real valued roots. And the situation with
which would have three dissimilar real valued roots. And the situation with 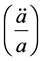 not equal to zero yields more tractable result for
not equal to zero yields more tractable result for 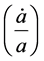 which will have implications for the HUP inequality in Pre-Planckian space-time, and buttresses an analysis of a 1 dimensional “time” mapping for emergent VEV (vacuum expectation values).
which will have implications for the HUP inequality in Pre-Planckian space-time, and buttresses an analysis of a 1 dimensional “time” mapping for emergent VEV (vacuum expectation values).
Keywords:
HUP, Dynamical Systems

1. First Looking at the 1 Dimensional Issue We Can Be Considering for Analysis. Leading up to dgtt
We will be following a first principle investigation of initial equations of state for energy density in space-time as given by B. Hu [1] which we write up as follows: Assuming that an energy density, in Pre-Planckian space-time is given by, if we have an averaged out mean frequency for particle production given by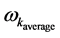 .
.
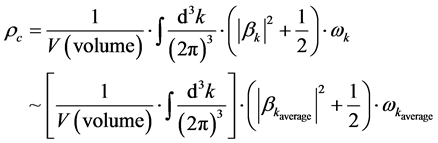 (1)
(1)
The second line of the above is making the approximation that the insides of the first line, are averaged out to a constant, which is defensible in the situation of a Pre- Planckian space-time condition. Secondly, we are assuming in all of this that  is the number of “created” particles in k space, in space-time is in terms of a situation for which we are assuming a very narrow range of k values, so we are when looking at the 2nd line of Equation (2) referencing an averaged out value for the number of created particles which we then identify as
is the number of “created” particles in k space, in space-time is in terms of a situation for which we are assuming a very narrow range of k values, so we are when looking at the 2nd line of Equation (2) referencing an averaged out value for the number of created particles which we then identify as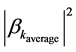 , and have
, and have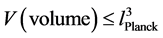 , i.e. with
, i.e. with 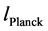 Planck length.
Planck length.
If so, then we could define having a net energy as given by [1]
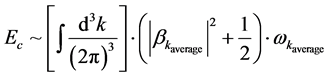 . (2)
. (2)
We have several different ways to address what is meant by this energy. Our supposition is that we could make a reference, here, to, if c (speed of light) = 1, to have, here, initially, a transfer of gravitons, as an information carrier, from a prior universe to our present universe so that as a result of a match up in Pre-Planckian space-time to Planckian space time we would have Equation (2) as rendered by, using Hu again, [1] .
 (3)
(3)
And a graviton count, in the Pre-Planckian era we would give as [1] .
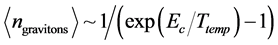 (4)
(4)
Here, we would have that 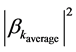 would be the “average” number of particles produced in the kth mode, and this kth mode would be in Pre-Planckian space-time. Then combining Equation (3) and Equation (4), if we wish to obtain a “Bose” representation of “gravitons” produced in the immediate aftermath of
would be the “average” number of particles produced in the kth mode, and this kth mode would be in Pre-Planckian space-time. Then combining Equation (3) and Equation (4), if we wish to obtain a “Bose” representation of “gravitons” produced in the immediate aftermath of 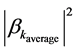 as the number of particles produced via a VEV, then we would have, if we have
as the number of particles produced via a VEV, then we would have, if we have .
.
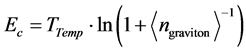 (5)
(5)
Then there would be the rough equivalence given of, say:
We will from here, state that this initial graviton production say for a Planck instant of time would be of the order of 105, so as to have, then if the temperature becomes
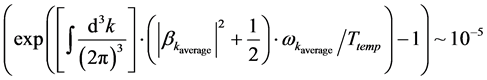 . (6)
. (6)
If

Then, the above reduces to the form of equivalencies which we will write up as follows, which will be accessed toward the end of this article.

Becomes
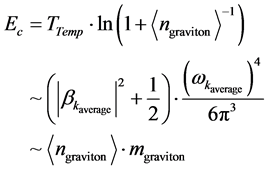
If one has a grasp of the number of VeV quasi particles where 
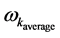
Our assumptions are that then we would have a way to, get bounds on 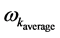
Our last part of information, using Hu again [1] - [3] is in picking the mass of a heavy graviton to be of the order of

Also the mass of 

We are then ready after some additional work to apply our HUP for Pre-Planckian metric tensor and to determine admissible
2. Introduction to the Friedman Problem and Also the HUP Connected with Metric Fluctuation
We will be examining a Friedmann equation for the evolution of the scale factor, using explicitly one case being when the acceleration of expansion of the scale factor is kept in, and the intermediate cases of when the acceleration factor, and the scale factor is important but not dominant. In doing so we will be tying it in our discussion with the earlier work done on the HUP but from the context of how the acceleration term will affect the HUP, and making sense of [2] .
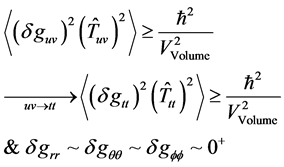
Namely we will be working with [2]

i.e. the fluctuation 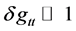

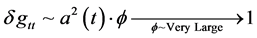
In short, we would require an enormous “inflation” style 



Then by [2] [7]

3. How Could Anyone Get the Acceleration of the Universe Factored into Our Scale Factor?
Begin looking at material from page 483-485 of [8]
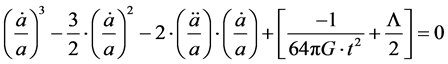
Then, consider two cases of what to do with the ration of 
1) Solutions for Equation (15), in Cubic form for Equation (15) gained by NOT abandoning
Following [2] [8] [9] look first at

Our approximation is, to set 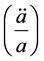
as a non-dimensional but very large quantity. Then a solution exists as given as for a reduced cubic version of Equation (15) which can be given by modifications as presented in this document. i.e. we are using material as given in [9] repeatedly as to solutions to the generalized cubic equation.
Our approximation is, to set 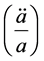
as a non-dimensional but very large quantity. Then a solution exists as given as for a reduced cubic version of Equation (15) which can be given by [9]
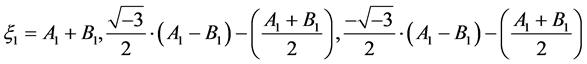
And
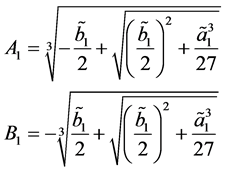
And when 
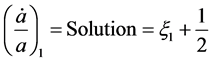
If so then
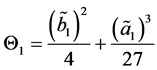
If 
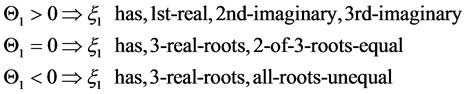
Here, with very large constant initial 
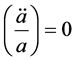
This means that in terms of Equation (21) especially if we have three unequal roots, for Equation (19) that the choice is, in acceleration for a chaotic environment [10] .
4. What Is the Argument against the Usual Heisenberg Uncertainty Principle?
Using [4] and take the limit of the variation to approach 1, then what do we get?
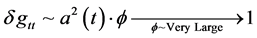
In short, we would require an enormous “inflation” style 
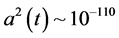
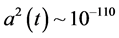
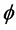
4.1. The Problem with Nearly Infinite Scalarfields Which Shows up in Super Symmetric Models
Going to Kolb, Pi, and Raby, [11] we outline certain problems with the usual SUSY models which in effect argues strongly against a scalar value 
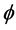

With a minimum value for Equation (23) according to the first derivative, 
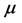
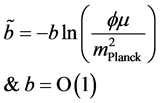
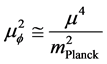
With a minimization of a SUSY style Equation (23), and Equation (26) below if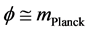
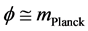
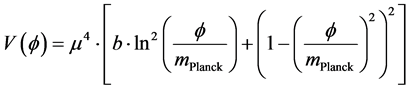
i.e. this is still, with some tweaking a commonly accepted SUSY VeV model, with a minimum if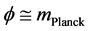
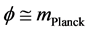
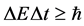
5. Treating Our Problem via Dynamical Systems Ideas
We will first of all, look at the inner dynamics of the metric tensor fluctuation. To do this we encompass the following background. We will next discuss the implications of this point in the next section, of a non-zero smallest scale factor. Secondly the fact we are working with a massive graviton, as given will be given some credence as to when we obtain a lower bound, as will come up in our derivation of modification of the values [2] .
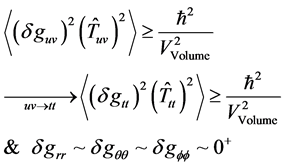
The reasons for saying this set of values for the variation of the non 
Begin with the starting point of [12] [13]

We will be using the approximation given by Unruh [12] [13] , of a generalization we will write as

If we use the following, from the Roberson-Walker metric [14] .

Following Unruh [12] [13] , write then, an uncertainty of metric tensor as, with the following inputs
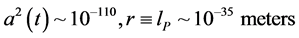
Then, if

This Equation (32) is such that we can extract, up to a point the HUP principle for uncertainty in time and energy, with one very large caveat added, namely if we use the fluid approximation of space-time [14] [15] .
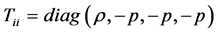
Then [2]
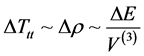
Then, Equation (32) and Equation (33) and Equation (34) together yield

How likely is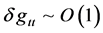
5.1. How We Can Justifying Writing Very Small 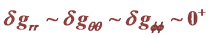
To begin this process, we will break it down into the following coordinates. In therr, θθ and 

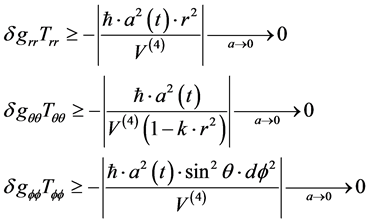
If as an example, we have negative pressure, with Trr, Tθθ and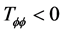

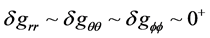
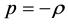
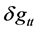
5.2. Considering Now the Reach of Dynamical Systems into This Problem. For δgtt
We will next be considering the role of a possible dynamical systems mapping upon this problem. To begin with, we will be looking at the role of 
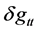


What is in Equation (37) shows from inspection that there is, defacto a 1 dimensional mapping for an initially three dimensional process, which is furthermore reflected in what is written up as of the frequency via the following, namely look at if



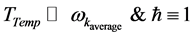

This can be put into Equation (37). A more conservative treatment of the above,
would be to write a constant, 
in Pre-Planckian space to write.

If so, then there would be an iterative map looking like

Given this iterative mapping, we can then state clearly its relationship to the Alexan- drov theorem, 1942, which the author was able to ascertain on January 29th at the Stony brook University weekly talk on Dynamical systems. What we heard is, simply, is that from this talk, that if we ask the following, namely:
Consider a 
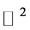

Theorem: Alexandrov, 1942:
Suppose 



i.e. see http://fillastre.u-cergy.fr/wp-content/uploads/2011/04/moscow-fillastre.pdf
The long and short of it is, that if we look at a quantum bounce “ball” of infinitely small radii, but not a point in space, that the relation given in Equation (39a) will define a metric fluctuation, 
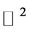
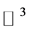





5.3. Looking at the Calabi-Yau Idealization of Early Universe Conditions and Equation (39a)
A singular manifold Calabi-Yau determines the physical characteristics of the topological soliton states that are interpreted as particles in high energy physics. i.e. what we are doing is when considering the graviton as a particle wave duality, in the formation of Equation (39a) and in doing so, we have to face up to the fact, that the gravitons, in string theory, and the Chalabi Yau setting are almost always massless. i.e. in addition, it is next to impossible for there to be any massive gravitons, since gravitons in this setting as given by [16] - [19] are almost always massless excitations of strings. Not only are we shorn of the geometric insight of the Alexandrov, 1942 theorem, [20] but we are also denied access to the visualization of the quantum bounce as provided by Bojowald, [21] in Nature, as of 2007, and assumed in this document as well as [22] . i.e. the Calabi Yau idealization depends upon massless particles for.
6. Lower Bound to the Graviton Mass Using Barbour’s Emergent Time
In order to start this approximation, we will be using Barbour’s value of emergent time [8] [9] restricted to the Plank spatial interval and massive gravitons, with a massive graviton [10]
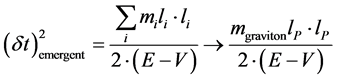
Initially, as postulated by Barbour [5] [6] , this set of masses, given in the emergent time structure could be for say the planetary masses of each contribution of the solar system. Our identification is to have an initial mass value, at the start of creation, for an individual graviton.
If 

Key to Equation (41) will be identification of the kinetic energy which is written as
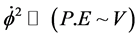
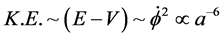
This is done with the proviso that w < −1, in effect, what we are saying is that during the period of the “Planckian regime” we can seriously consider an initial density proportional to Kinetic energy, and call this K.E. as proportional to [2]

If we are where we are in a very small Planckian regime of space-time, we could, then say write Equation (43) as proportional to 
7. Conclusion. Considering Einstein Space, and Further Research Questions
A way of solidifying the approach given here, in terms of early universe GR theory is to refer to Einstein spaces, via [14] [23] as well as to make certain of the Stress energy tensor [15] as we can write it as a modified Einstein field equation. Then, 

Here, the term in the Left hand side of the metric tensor is a constant, so then if we write, with R also a constant [24] .

So as to recover, via the Einstein spaces, the seemingly heuristic argument is given above. Furthermore when we refer to the Kinetic energy space as an inflation 

In the case of the general elliptic operator K if we are using the Fulling reference, [26] in the case of the above Roberson-Walker metric, with the results that the elliptic operator, in this case become,

Then, according to [26] , if R above, in Equation (47) is initially a constant, we will see then, if m is the inflation mass, that

Then 


If the frequency, of say, Gravitons is of the order of Planck frequency, then this term, would likely dominate Equation (49). More of the details of this will be worked out, and also candidates for the 
The details of the elliptic operator K will be gleaned from [14] [15] [26] whereas the details of inflation 
It is important to note, that the proper evaluation of Equation (49) will permit, once the role of gravitons in the changing of an inflation contribution is thoroughly experimentally vetted for us to analyze if the criteria raised in [30] are satisfied. As well as understanding the scalar-tensor theories of gravity which are alluded to, in [30] , which have to be either falsified or confirmed. Finally note that what we are doing is an extension of [31] , i.e. GW are experimentally confirmed, and it is necessary to pay attention to the issue of stochastic contributions to signal noise.
i.e. quote:
Binary black hole systems at larger distances contribute to a stochastic background of gravitational waves from the superposition of unresolved systems.
End of quote.
Thoroughly understanding the role of Equation (49) has to be done as to avoid a similar issue here, especially when the emergence of the inflation, as presupposed may significantly add to stochastic noise.
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.
Cite this paper
Beckwith, A.W. (2016) Gedanken Experiment for Looking at dgtt for Initial Expansion of the Universe and Influence on HUP via Dynamical Systems, with Positive Pre-Planckian Acceleration. Journal of High Energy Physics, Gravitation and Cosmology, 2, 531-545. http://dx.doi.org/10.4236/jhepgc.2016.24046
References
- 1. Hu, B. (1984) Vacuum Viscosity and Entropy Generation in Quantum Gravitational Pro- cesses in the Early Universe. In: Fang, L.Z. and Ruffini, R., Eds., Cosmology of the Early Universe, World Press Scientific, Singapore, 23-44.
- 2. Beckwith, A. (2016) Gedanken Experiment for Refining the Unruh Metric Tensor Uncertainty Principle via Schwartz Shield Geometry and Planckian Space-Time with Initial Nonzero Entropy and Applying the Riemannian-Penrose Inequality and Initial Kinetic Energy for a Lower Bound to Graviton Mass (Massive Gravity). Journal of High Energy Physics, Gravitation and Cosmology, 2, 106-124.
http://dx.doi.org/10.4236/jhepgc.2016.21012 - 3. Goldhaber, A. and Nieto, M. (2010) Photon and Graviton Mass Limits. Reviews of Modern Physics, 82, 939-979.
http://arxiv.org/abs/0809.1003
http://dx.doi.org/10.1103/revmodphys.82.939 - 4. Giovannini, M. (2008) A Primer on the Physics of the Cosmic Microwave Background. World Press Scientific, Hackensack. http://dx.doi.org/10.1142/6730
- 5. Barbour, J. (2009) The Nature of Time. http://arxiv.org/pdf/0903.3489.pdf
- 6. Barbour, J. (2010) Shape Dynamics: An Introduction. In: Finster, F., Muller, O., Nardmann, M., Tolksdorf, J. and Zeidler, E., Eds., Quantum Field Theory and Gravity, Conceptual and Mathematical Advances in the Search for a Unified Framework, Birkhauser, Springer-Ver- lag, London, 257-297.
- 7. Handley, W.J., Brechet, S.D., Lasenby, A.N. and Hobson, M.P. (2014) Kinetic Initial Conditions for Inflation. http://arxiv.org/pdf/1401.2253v2.pdf
- 8. Ringstrom, H. (2013) On the Topology and Future Stability of the Universe. Oxford Science Publications, Oxford. http://dx.doi.org/10.1093/acprof:oso/9780199680290.001.0001
- 9. Beyer, W. (1990) CRC Standard Mathematical Tables. 28th Edition, CRC Press, Boca Raton.
- 10. Katok, A. and Hasselblatt, B. (1999) Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, New York.
- 11. Kolb, E., Pi, S.-Y. and Raby, S. (1984) Phase Transitions in Supersymmetric Grand Unified Models. In: Zhi, F.L. and Ruffini, R., Eds., Cosmology of the Early Universe, World Press Scientific, Hong Kong.
- 12. Unruh, W.G. (1986) Why Study Quantum Theory? Canadian Journal of Physics, 64, 28-130.
http://dx.doi.org/10.1139/p86-019 - 13. Unruh, W.G. (1986) Erratum: Why Study Quantum Gravity? Canadian Journal of Physics, 64, 1453.
http://dx.doi.org/10.1139/p86-257 - 14. Gutfreund, H. and Renn, J. (2015) The Road to Relativity, the History and Meaning of Einstein’s “The Foundation of General Relativity” (Featuring the Original Manuscript of Einstein’s Masterpiece). Princeton University Press, Princeton. http://dx.doi.org/10.1515/9781400865765
- 15. Griffiths, J. and Podolsky, J. (2009) Exact Space-Times in Einstein’s General Relativity. Cambridge Monographs in Mathematical Physics, Cambridge. http://dx.doi.org/10.1017/CBO9780511635397
- 16. http://fillastre.u-cergy.fr/wp-content/uploads/2011/04/moscow-fillastre.pdf
- 17. Morrison, D.R. and Vafa, C. (1996) Compactifications of F-Theory on Calabi-Yau Threefolds (I). Nuclear Physics B, 473, 74-92. http://dx.doi.org/10.1016/0550-3213(96)00242-8
- 18. Morrison, D.R. and Vafa, C. (1996) Compactifications of F-Theory on Calabi-Yau Threefolds (II). Nuclear Physics B, 476, 437-469. http://dx.doi.org/10.1016/0550-3213(96)00369-0
- 19. Klemm, A. and Schimmrigk, R. (1994) Landau-Ginzburg String Vacua. Nuclear Physics B, 411, 559-583. (E-Print arXiv:hep-th/9204060)
- 20. http://www.aei.mpg.de/~theisen/lectures.pdf
- 21. Bojowald, M. (2007) What Happened before the Big Bang? Nature Physics, 3, 523-525.
http://dx.doi.org/10.1038/nphys654 - 22. http://www.nature.com/news/quantum-bounce-could-make-black-holes-explode-1.15573
- 23. Penrose, R. (2010) Cycles of Time: An Extraordinary New View of the Universe. The Bodley Head, London.
- 24. Petrov, A.Z. (1969) Einstein Spaces. Pergamon Press, Oxford.
- 25. Gorbunov, D. and Rubakov, V. (2011) Introduction to the Theory of the Early Universe, Cosmological Perturbations and Inflationary Theory. World Scientific Publishing Pte. Ltd., Singapore.
http://dx.doi.org/10.1142/7873 - 26. Fulling, S.A. (1991) Aspects of Quantum Field Theory in Curved Space-Time. London Mathematical Society Student Texts 17. Cambridge University Press, Cambridge.
- 27. Wald, R.M. (1994) Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics. University of Chicago Press, Chicago.
- 28. Fredenhagen, K. and Rejzner, K. (2010) Local Covariance and Background Independence. In: Finster, F., Muller, O., Nardmann, M., Tolksdorf, J. and Zeidler, E., Eds., Quantum Field Theory and Gravity, Conceptual and Mathematical Advances in the Search for a Unified Framework, Springer-Verlag, London, 15-23.
- 29. Corda, C. (2012) Primordial Gravity’s Breath. Electronic Journal of Theoretical Physics, 9, 1-10.
http://arxiv.org/abs/1110.1772 - 30. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282.
http://dx.doi.org/10.1142/S0218271809015904 - 31. Abbott, B.P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016) Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters, 116, 061102.
https://physics.aps.org/featured-article-pdf/10.1103/PhysRevLett.116.061102
http://dx.doi.org/10.1103/PhysRevLett.116.061102