Journal of High Energy Physics, Gravitation and Cosmology
Vol.03 No.02(2017), Article ID:75507,11 pages
10.4236/jhepgc.2017.32024
Extra Dimensions, Brane Worlds, and the Vanishing of Axion Contributions to Inflation
Andrew Walcott Beckwith
Physics Department, College of Physics, Chongqing University Huxi Campus, Chongqing, China

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 17, 2017; Accepted: April 17, 2017; Published: April 20, 2017
ABSTRACT
We examine from first principles the implications of the 5th Randall Sundrum Brane world dimension in terms of setting initial conditions for chaotic inflationary physics. Our model pre-supposes that the inflationary potential pioneered by Guth is equivalent in magnitude in its initial inflationary state to the effective potential presented in the Randall-Sundrum model. We also consider an axion contribution to chaotic inflation (which may have a temperature dependence) which partly fades out up to the point of chaotic inflation being matched to a Randall-Sundrum effective potential. If we reject an explicit axion mass drop off to infinitesimal values at high temperatures, we may use the Bogomolnyi inequality to re-scale and re-set initial conditions for the chaotic inflationary potential. One of the potential systems embedded in the Randall-Sundrum brane world is a model with a phase transition bridge from a tilted washboard potential to the chaotic inflationary model pioneered by Guth which is congruent with the slow roll criteria. If, as written up earlier, the axion wall contribution is due to di-quarks, which is equivalent to tying in baryogenesis to the formation of chaotic inflation initial conditions, with the Randall-Sundrum brane world effective potential delineating the end of the dominant role of di-quarks, and the beginning of inflation.
Keywords:
Extra Dimensions, Brane Worlds, Axion Contributions

1. Introduction
This investigation is attempting to show that the fifth dimension postulated by Randall-Sundrum theory helps give us an action integral which leads to a minimum physical potential we can use to good effect in determining initial conditions for the onset of inflation. The 5th dimension of the Randall-Sundrum brane world is of the genre, for 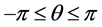
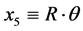 (1)
(1)
This leads to an additional embedding structure for typical GR fields, assuming as one may write up a scalar potential “field” with  real valued, and the rest of it complex valued as [1]
real valued, and the rest of it complex valued as [1]
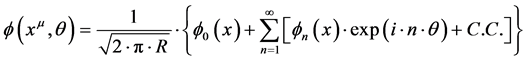 (2)
(2)
This scalar field makes its way to an action integral structure which will be discussed later on, which Sundrum used to forming an effective potential. Our claim in this analysis can also be used as a way of either embedding a Bogomolyni inequality, perhaps up to five dimensions [2] or a straight forward reduction in axion mass due to a rise in temperature [3] helping reduce effective potential in this structure, with the magnitude of the Sundrum potential forming an initial condition for the second potential of the following phase transition. Note that we are referring to a different form of the scalar potential, which we will call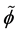 , which has the following dynamic [4] .
, which has the following dynamic [4] .
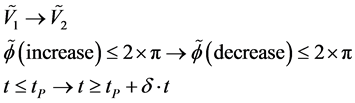 (3)
(3)
The potentials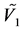 , and
, and 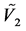 were described in terms of S-S’ di-quark pairs nucleating and then contributing to a chaotic inflationary scalar potential system. Here,
were described in terms of S-S’ di-quark pairs nucleating and then contributing to a chaotic inflationary scalar potential system. Here, 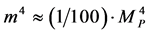
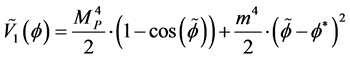 (3a)
(3a)
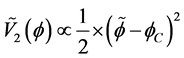 (3b)
(3b)
We should keep in mind that  in Equation (3a) is an equilibrium value of a true vacuum minimum of Equation (3a) after tunneling. In the potential system given as E Equation (3a) we see a steadily rising scalar field value which is consistent with the physics of Equation (3a) and Equation (3b) which qualitatively adhere to what we want for Equation (3). In the potential system given by Equation (3b) we see a reduction of the “height of a scalar field which is consistent with the chaotic inflationary potential overshoot phenomena”. We should note that
in Equation (3a) is an equilibrium value of a true vacuum minimum of Equation (3a) after tunneling. In the potential system given as E Equation (3a) we see a steadily rising scalar field value which is consistent with the physics of Equation (3a) and Equation (3b) which qualitatively adhere to what we want for Equation (3). In the potential system given by Equation (3b) we see a reduction of the “height of a scalar field which is consistent with the chaotic inflationary potential overshoot phenomena”. We should note that 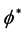 in Equation (3a) is a measure of the onset of quantum fluctuations. Appendix I is a discussion of Axion potentials which we claim that is part of the contribution of the potential given in Equation (3a). Note that the tilt to the potential given in Equation (3a) is due to a quantum fluctuation. As explained by Guth for quadratic potentials [5] ,
in Equation (3a) is a measure of the onset of quantum fluctuations. Appendix I is a discussion of Axion potentials which we claim that is part of the contribution of the potential given in Equation (3a). Note that the tilt to the potential given in Equation (3a) is due to a quantum fluctuation. As explained by Guth for quadratic potentials [5] ,
 (3c)
(3c)
This in the context of the fluctuations having an upper bound of
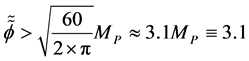 (3d)
(3d)
Here, . Also, the fluctuations Guth had in mind were modeled via [6]
. Also, the fluctuations Guth had in mind were modeled via [6]
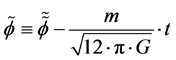 (3e)
(3e)
In the potential system given by Equation (3b) we see a reduction of the “height” or magnitude of a scalar field which is consistent with the chaotic inflationary potential overshoot phenomena mentioned just above. This leads us to use the Randal-Sundrum effective potential [1] in tandem with tying in baryogenesis [7] to the formation of chaotic inflation initial conditions for Equation (3b), with the Randall-Sundrum brane world effective potential delineating the end of the dominant role of di-quarks, due to baryogenesis, and the beginning of inflation. The role of the Bogomolnyi inequality is to introduce, from a topological domain wall standpoint, a mechanism for the introduction of baryogenesis in early universe models. The combination of that analysis, plus matching conditions with the Randal-Sundrum effective potential, sets us up for chaotic inflation.
2. How to Form the Randall-Sundrum Effective Potential
The consequences of the fifth dimension mentioned in Equation (1) above show up in a simple warped compactification involving two branes, i.e. a Planck world brane, and an IR brane. This construction with the physics of this 5 dimensional system allow for solving the hierarchy problem of particle physics, and in addition permits us to investigate the following five dimensional action integral [1] .
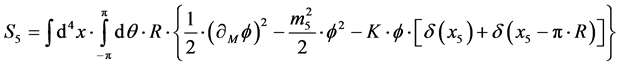 (4)
(4)
This integral, will lead to the following equation to solve

Here, what is called 

This uses [8] (assuming 

This is for a compactification scale, for

We then obtain after a non trivial vacuum averaging [8]


This is leading to an initial formulation of

Now, if one is looking at an addition of a 2nd scalar term of opposite sign, but of equal magnitude [1]

This is for when we set up an effective Randall-Sundrum potential looking like [1]

This above system has a Meta stable vacuum for a given special value of 
3. How to Compare the Randall-Sundrum Effective Potential Minimum with an Effective Potential Minimum Involving the Potential of Equation (3) above
We are forced to consider two possible routes to the collapse of a complex potential system to the chaotic inflationary model promoted by Guth [5] .
The first such model involves a simple reduction of the axion wall potential [9] as given by, especially when N = 1

The simplest way to deal with Equation (13) is to set

i.e. to declare that the axion “mass” vanishes, and to let this drop off in value give a simple truncated version of chaotic inflationary potentials along the lines given by a transition from Equation (3a) to Equation (3b) We should note that 


has a bearing on this situation. Not to mention the problems inherent in several proposed fixes to the cosmological constant problem [13] .
Now if we want an equivalent explanation, which may involve baryogenesis, we need to look at the component behavior of each of the terms in Equation (13) without assuming

We then have to present a varying in magnitude value for the ‘scalar’ 

There has been credible work with instantons in higher dimensions, starting with Hawkings 1999 article [14] this, however, addresses a way of linking an instanton structure with baryogenesis, dark energy, and issues of how Randall-Sundrum brane structure can be used to formation of initial conditions of inflationary cosmology.
Clarifying what can be done with an instanton style quantum nucleation in multiple dimensions [15] may help us with more acceptable models [7] [16] as to estimating, roughly, a quantum value for the cosmological constant, as an improvement in recent calculations.


where

This leads, if done correctly to the quadratic sort of potential contribution as given by [16] . At the same time it raises the question of if or not when there is a change from the 1st to the 2nd potential system, we have a consistent model. Let us now view a toy problem involving use of a S-S’ pair which we may write as [17]

This is for a di-quark pair along the lines given when looking at the first potential system, which is a takeoff upon Zhitinisky’s color super conductor model [18] .
4. Comparison of Initial Conditions for a Nucleating Universe
Now for the question the paper is raising, Can we realistically state the following for initial conditions of a nucleating universe? If so, then what are the consequences?

The right hand side of Equation (20) can be stated as having

We can insist that this 

So, this leads to the following question. Does a reduction of axion wall mass for the first potential system given in Equation (3a) being transformed to Equation (3b) above give us consistent physics, due to temperature dependence in axion “mass”, or should we instead look at what can be done with S-S’ instanton physics and the Bogolmyi inequality [20] in order to perhaps take into account Baryogenesis? Also, can this shed light upon the Wheeler De Witt’s equations [21] modification by Ashtekar [22] in early universe quantum bounce conditions?
Finally, does this process of baryogenesis, if it occurs lend then to the regime where there is a bridge between classical applications of the Wheeler De Witt equation to the quantum bounce condition raised by Ashtekar [22] ?
5. Tie in with the Wheeler De-Witt Equation
Abbay Ashtekar’s quantum bounce [22] gives a discretized version of the Wheeler De Witt equation. Let us first review classical De Witt theory which ties in with inflationary n = 2 scalar potential field cosmology. This will be useful in analyzing consequences of the wave functional so formed in Equation (18) and suggest quantum bounce analogies we will comment upon later.
In the common versions of Wheeler De Witt theory a potential system using a scale radius


Here we have that

As well as

Now, Alfredo B. Henriques [16] presents a way in which one can obtain a Wheeler De Witt equation based upon

Using a momentum operator as give by

This is assuming a real scalar field 




As well as an energy term


This is for a “cosmic” Schrodinger equation as given by

This has

and

Here 



Now Ashtekar in his longer arXIV article [24] make reference to a revision of this momentum operation along the lines of basis vectors 

With the advent of this re definition of momentum we are seeing what Ashtekar works with as a sympletic structure with a revision of the differential equation assumed in Wheeler-De Witt theory to a form characterized by [26]



Also, and more importantly this 

This is for a crucial “momentum” value

And

which leads to, for an initial point in “trajectory space” given by the following relation 
So that if we consider eignfunctions of the De Witt (difference) operator, as contributing toward

With each 


This equation above has a “symmetry” as seen in Figure 1 of Ashtekar’s PRL article [6] about

6. Conclusion
We are presenting a question which may be of relevance to JDEM research. Namely if Ashtekar is correct in his quantum geometry [24] , and the breakdown of early universe conditions not permits the typical application of the Wheeler De Witt equation, then what do we have to verify it experimentally? The axion wall dependence so indicated above may provide an answer to that, and may be experimentally measurable via Kadotas pixel reconstructive scheme [25] .
Furthermore, we also argue that the semi-classical analysis of the initial potential system as given by Equation (3) above and its subsequent collapse is de facto evidence for a phase transition to conditions allowing for dark energy to be created at the beginning of inflationary cosmology [26] [27] . This builds upon an earlier paper done by Kolb in minimum conditions for reconstructing scalar potentials [28] [29] [30] . It also will necessitate reviewing other recent derivation bound to the cosmological constant in cosmology model in a more sophisticated manner than that has been presently done [31] . In doing so, it may be appropriate to try to reconcile A. Ashtekar’s approach involving a discretization of the Wheeler De Witt equation with the bounce calculations in general cosmology pioneered by Hackworth and Weinberg [32] . Needless to say, the work so presented above leaves open the question if or not baryogenesis, is involved in involving a collapse of the first term of Equation (3a) along the lines of the Bogomolnyi inequality, or else we have to skip this and to adhere to the topological defect models pioneered by Trodden, et al. [33] [34] [35] .
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.
Cite this paper
Beckwith, A.W. (2017) Extra Dimensions, Brane Worlds, and the Vanishing of Axion Contributions to Inflation. Journal of High Energy Physics, Gravitation and Cosmology, 3, 285-295. https://doi.org/10.4236/jhepgc.2017.32024
References
- 1. Sundrum, R. (2005) Extra Dimensions. SLAC Summer Institute: Gravity in the Quantum World and the Cosmos, Stanford, 25 July-5 August 2005. http://www-conf.slac.stanford.edu/ssi/2005/lec_notes/Sundrum1/sundrum1.pdf
- 2. Lee, J. and Sorkin, R.D. (1988) Derivation of a Bogomol’ny Inequality in Five-Dimensional Kaluza-Klein Theory. Communications in Mathematical Physics, 116, 353-364. https://doi.org/10.1007/BF01229199
- 3. Kolb, E.W. and Turner, M.S. (1990) The Early Universe. Westview Press, Boulder.
- 4. Beckwith, A.W. (2006) How One Can Use Di Quark Scalar Fields Permitting a Cosmological Constant Permitting Gravitons Escaping from Early Universe Branes. 36th COSPAR Scientific Assembly, Beijing, 16-23 July 2006.
- 5. Guth, A.H. (1981) Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Physical Review D, 23, 347-356. https://doi.org/10.1103/physrevd.23.347
- 6. Guth, A.H. and Weinberg, E. (1983) Could the Universe Have Recovered from a Slow First-Order Phase Transition? Nuclear Physics B, 212, 321-364. https://doi.org/10.1016/0550-3213(83)90307-3
- 7. Carroll, S. (2014) Space-Time and Geometry: An Introduction to General Relativity. Pearson Education Limited, London, UK.
- 8. Maartens, R. (2005) Brane World Cosmology. In: Papantonopoulos, E. (Ed.), The Physics of the Early Universe, Lecture Notes in Physics, Vol. 653, Springer Verlag, Berlin, 213-249.
- 9. Kolb, E.W. and Turner, M.S. (1990) The Early Universe. Westview Press, Boulder.
- 10. Brown, L.S. (1992) Quantum Field Theory. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511622649
- 11. Carroll, S.M., Press, W.H. and Turner, E.L. (1992) The Cosmological Constant. Annual Review of Astronomy and Astrophysics, 30, 499-542. https://doi.org/10.1146/annurev.aa.30.090192.002435
- 12. Volovik, G. (2006) Vacuum Energies; Myths and Realities. International Journal of Modern Physics D, 15, 1987-2010.
- 13. Gurzadyan, G. and Xue, S.-S. (2003) On the Estimation of the Current Value of the Cosmological Constant. Modern Physics Letters A, 18, 561-568. https://doi.org/10.1142/S0217732303008405
- 14. Hawkings, S.W. and Real, H.S. (1999) Inflation, Singular Instantons and Eleven Dimensional Cosmology. Physical Review D, 59, Article ID: 023502. https://doi.org/10.1103/PhysRevD.59.023502
- 15. Mukhanov, V. (2005) Physical Foundations of Cosmology. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511790553
- 16. Henriques, A.B. (2006) Loop Quantum Cosmology and the Wheeler-De Witt Equation. General Relativity and Gravitation, 38, 1645-1659.
- 17. Beckwith, A.W. (2006) An Open Question: Are Topological Arguments Helpful in Setting Initial Conditions for Transport Problems in Condensed Matter Physics? Modern Physics Letters B, 29, 233-243. https://doi.org/10.1142/s0217984906010585
- 18. Zhitinisky, A.R. (2002) Dark Matter as Dense Color Superconductor.
- 19. Coleman, S. (1977) The Fate of the False Vacuum. Physical Review D, 15, 2929. https://doi.org/10.1103/PhysRevD.15.2929
- 20. Zee, A. (2003) Quantum Field Theory in a Nutshell. Princeton University Press, Princeton, 279-280.
- 21. Dalarsson, M. and Dalarsson, N. (2005) Tensors, Relativity, and Cosmology. Elsevier Press, Amsterdam.
- 22. Ashtekar, A., Pawlowiski, T. and Singh, P. (2006) Quantum Nature of the Big Bang. Physical Review Letters, 96, Article ID: 141301.
- 23. Thieumann, T. (1998) Quantum Spin Dynamics (QSD): V. Quantum Gravity as the Natural Regulator of the Hamiltonian Constraint of Matter Quantum Field Theories. Classical and Quantum Gravity, 15, 1281.
- 24. Ashtekar, A., Pawlowsk, T. and Singh, P. (2006) Quantum Nature of the Big Bang: An Analytical and Numerical Investigation I. Physical Review D, 73, Article ID: 124038.
- 25. Kadota, K., Dodelson, S., et al. (2005) Physical Review D, 72, Article ID: 023510.
- 26. Albrecht, A. and Bernstein, G. (2007) Evaluating Dark Energy Probes Using Multi-Dimensional Dark Energy Parameters. Physical Review D, 75, Article ID: 103003. https://arxiv.org/abs/astro-ph/0608269
- 27. Beckwith, A.W. (2006) How S-S’ Di Quark Pairs Signify an Einstein Constant Dominated Cosmology, and Lead to New Inflationary Cosmology Physics. Electronic Journal of Theoretical Physics, 9, 7-33.
- 28. Kolb, E.W. (1995) Deducing the Value of the Cosmological Constant during Inflation from Present-Day Observations. In: Suginohara, K. and Sugiyama, N., Eds., The Cosmological Constant and the Evolution of the Universe, Universal Academy Press, Tokyo, 169.
- 29. Kolb, E.W. (1995) From the Big Bang to Now, and the Journey Back. International Workshop on Elementary Particle Physics: Present and Future, Valencia, 5-9 June 1995, 371-382.
- 30. Kolb, E.W. and Turner, M.S. (1990) The Early Universe. Westview Press, Boston, MA.
- 31. Kolb, E.W. (1995) Potential Reconstruction. In: Giovannelli, F. and Manochii, Eds., Objects in Astrophysics and Particle Physics, Editrice Compositori, Bologna, 3.
- 32. Hackworth, C. and Weinberg, E.J. (2004) Oscillating Bounce Solutions and Vacuum Tunneling in de Sitter Space-Time.
- 33. Trodden, M. (2006) The Cosmology-Particle Physics Connection. http://arxiv.org/abs/hep-ph/0605284
- 34. Trodden, M. (1999) Dirichlet Solitons in Field Theories. https://arxiv.org/abs/hep-th/9901062
- 35. Bowick, M., De Filice, A. and Trodden, M. (2003) The Shapes of Dirichlet Defects. http://cds.cern.ch/record/625152/files/0306224.pdf
Appendix I
Forming an axion potential term as part of the contribution to Equation 2A
Kolb’s book [9] has a discussion of an Axion potential given in his Equation (10.27)

Here, he has the mass of the Axion potential as given by 

Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jhepgc@scirp.org


