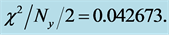Journal of High Energy Physics, Gravitation and Cosmology
Vol.02 No.02(2016), Article ID:65598,27 pages
10.4236/jhepgc.2016.22022
Cosmic Time Transformations in Cosmological Relativity
Firmin J. Oliveira
East Asian Observatory, Hilo, HI, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 November 2015; accepted 16 April 2016; published 19 April 2016
ABSTRACT
The relativity of cosmic time is developed within the framework of Cosmological Relativity in five dimensions of space, time and velocity. A general linearized metric element is defined to have the form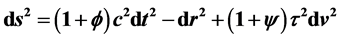 , where the coordinates are time t, radial distance
, where the coordinates are time t, radial distance 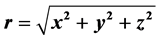 for spatials x, y and z, and velocity v, with c the speed of light in vacuum and
for spatials x, y and z, and velocity v, with c the speed of light in vacuum and  the Hubble-Carmeli time constant. The metric is accurate to first order in
the Hubble-Carmeli time constant. The metric is accurate to first order in 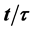 and
and . The fields
. The fields 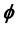 and
and 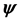 are general functions of the coordinates. By showing that
are general functions of the coordinates. By showing that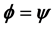 , a metric of the form
, a metric of the form 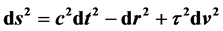 is obtained from the general metric, implying that the universe is flat. For cosmological redshift z, the luminosity distance relation
is obtained from the general metric, implying that the universe is flat. For cosmological redshift z, the luminosity distance relation  is used to fit combined distance moduli from Type 1a supernovae up to
is used to fit combined distance moduli from Type 1a supernovae up to 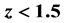 and Gamma-Ray Bursts up to
and Gamma-Ray Bursts up to , from which a value of
, from which a value of 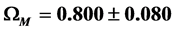 is obtained for the matter density parameter at the present epoch. Assuming a baryon density of
is obtained for the matter density parameter at the present epoch. Assuming a baryon density of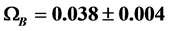 , a rest mass energy of
, a rest mass energy of  is predicted for the anti-baryonic
is predicted for the anti-baryonic  and the
and the 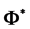
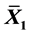

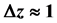

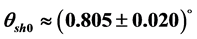
Keywords:
Flat Space, Cosmic Time, Time Dilation, Dark Matter
1. Introduction
It has recently been reported [1] on the apparent null effect of cosmic time dilation upon light curve power spectra measurements of some 800 low and high redshift quasars (QSO) monitored for 28 years. This appears to contradict two Supernovae Type Ia (SNe-Ia) light curve evolution studies [2] [3] which show the effect of
broadening of the power spectra time series consistent with a cosmic time dilation of 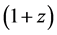
this paper, we show that both the QSO and SNe-Ia results are compatible if account is made for the relativity of cosmic time as developed in the theory of Cosmological Special Relativity (CSR) [4] . We also apply these concepts to fitting the combination of high redshift SNe-Ia distance data [5] and Gamma-Ray Bursts (GRB) data [6] .
The Cosmological Relativity of Carmeli [7] , the general and special theories, is a five dimensional brane world model based on time t, space 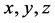

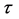
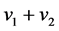
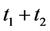
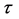
In this paper, we derive only the minimum CSR framework we require for the development of cosmic time transformation effects and the luminosity distance relation. We show that for weak fields 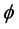
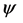


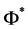
2. The Universe
The five dimensional Cosmological General Relativity of Carmeli [7] is approximated by the linearized metric element,
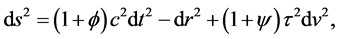
where
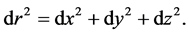
The coordinates are time t, spatials x, y and z and velocity v, with c the speed of light in vacuum and 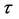
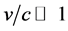
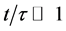

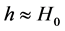

Hubble constant. The fields 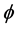
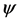
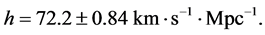
This gives

In Cosmological Relativity the time coordinate is measured backwards from the present at 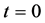
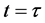
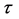
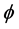
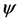
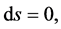
and it is observed at a specific cosmic time t, so that
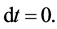
Applying (5) and (6) to (1) yields for the expanding universe
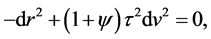
which reduces to
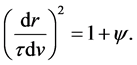
The metric (1) defines the Einstein field equations in five dimensions [7] (Sect. 7.3)
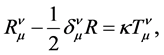
where 
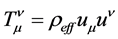
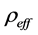
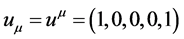

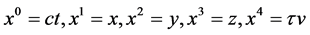
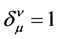
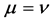
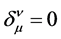
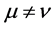
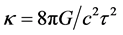
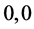

where

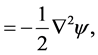
where 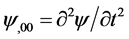

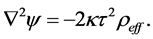
The effective mass density is defined by
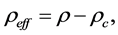
where 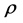
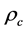

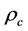
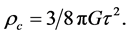
It is useful to express the effective mass density as a parameter in terms of the critical mass density. Dividing by 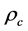
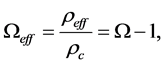
where 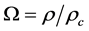
where M is an optional point mass centered at the origin of r. Assuming no central mass, we set
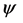
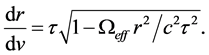
3. General Solution in Space-Velocity
The integration of (18) over r and v in the space-velocity domain is carried out at a specific time t. We assume that the mass density 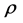
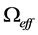
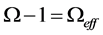
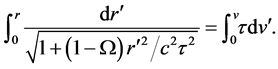
Integrating (19) and solving for r in terms of v we obtain the general solutions
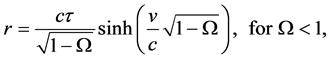
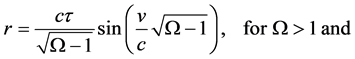
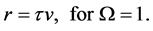
By use of the identities 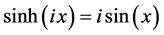


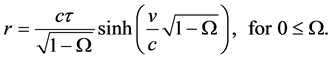
4. Flat Space Metric
Equation (17) gave the solution for the field
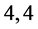
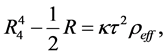
where
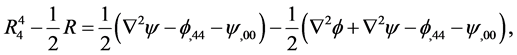
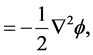
where 
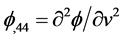
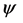
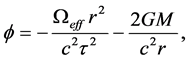
where M is an optional point mass centered at the origin of r. We see by (17) and (27) that in fact,
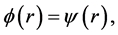
and furthermore, that the constants c and 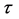

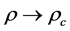
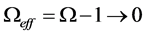
On the other hand, more generally, we can derive a flatspace metric. Given (28), if we divide (1) by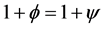
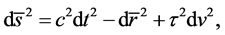
where
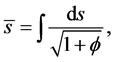
and
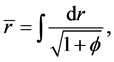
with the condition that
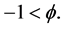
This implies that for weak fields 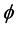
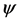
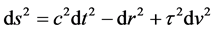
5. The Cosmological Special Relativistic Transformation
By (29), with notation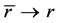
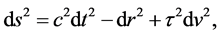
where r is given by (31). The expansion of the universe occurs when 
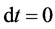
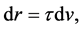
which, upon integration gives the Hubble law
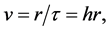
where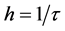
In the observable universe there are two classes of objects, those that are bounded by the gravitation of their combined masses and those that are observed to be moving away from one another in the Hubble flow. In other words, if we lump all nearby neighboring galaxies into a super galaxy mass point, then the universe would consist of only super galaxy mass points flying apart in the Hubble flow. Cosmological Special Relativity (CSR) describes these super galactic objects in the universe. However, unlike SR which can have real observers in reference frames which move relatively at less than light speed, in CSR, all galaxies are in the Hubble flow and expand at the Hubble rate h. That is, there are no objects not in the Hubble flow from which to set up a frame of reference and compare observations. Consequently, for CSR we define hypothetical observers in their frames which move relatively at a rate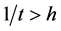
In CSR the age of the universe is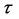
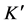
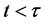
describing an object O with “4-vector” coordinates 

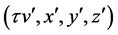

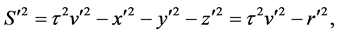
with the invariant condition
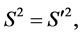
where 

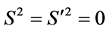

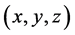
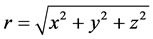
To obtain the cosmological transformation ( [7] , Sect. 2.2), analogous with the Lorentz transformation, assume that a linear transformation exists between the coordinates of hypothetical frames K and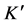

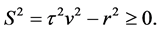
Similarly, in frame 
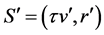
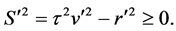
By the requirement that the magnitude of a 4-vector is invariant under transformations between reference frames then
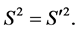
Clearly, by (39) and (40), the 4-vectors S and 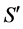

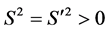
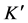
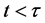
Then, for constants 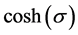
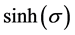
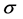

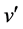
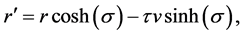
and
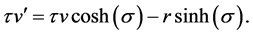
To solve for the angle 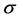
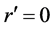
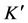
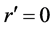
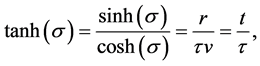
where

is the fixed cosmic time separating the origins of frame 
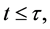
where 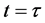
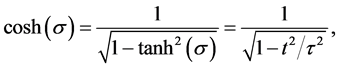
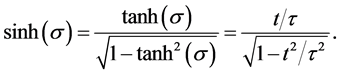
Substituting from (47) and (48) into (42) and (43) we obtain
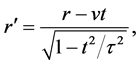

By inverting (49) and (50) we get the inverse transform equations
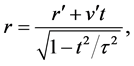
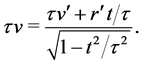
It can be verified that the transformations (49)-(52) satisfy the invariance requirement of (41) that 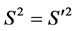
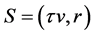
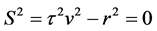
gives for the galaxy O observed in 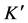
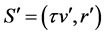

6. Cosmological Redshift of Light
We wish to quantify observations of light wave phenomena in the expanding universe made by observers at different cosmic times. Consider the distance r to a galaxy O which is in the Hubble flow, measured by the observer at the origin of K. For the observer at the origin of 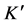
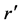

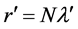
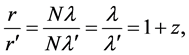
where z is the cosmological redshift of the light due to the expansion of space during the cosmic time t between frames 


For a galaxy which is in the Hubble flow,

Substituting from (56) into (55), and along with (53) yields

Equation (57) is the cosmological redshift of the wavelength of light measured between observers in frames K and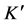

7. Dilation of Cosmic Time Due to the Expansion of Space
This transformation is similar to the lengthening of the wavelength of light from a distant galaxy by the factor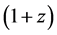
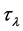
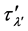

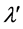
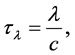
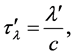
we have from (53),
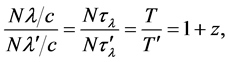
where 
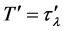
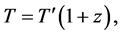
where we assume that 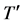

8. Relativity of Cosmic Time
Dividing (51) by (52) we obtain the transformation for the addition of cosmic time from 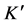
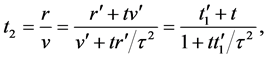
where

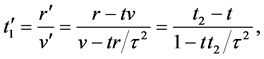
where
Setting 
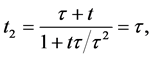
implying that two cosmic times can never add up to more than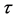
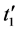
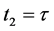
8.1. Contraction of a Small Interval of Cosmic Time in the Past
An increase in cosmic time t by 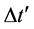

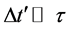
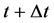
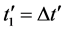
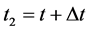
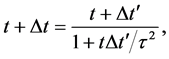
which yields
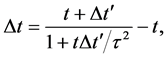

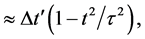
since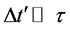

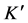
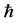
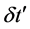
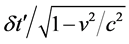
8.2. Dilation of a Small Interval of Cosmic Time in the Present
There is a second kind of effect of time addition which is measured by the observer in 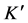
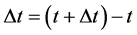

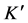
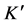
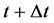

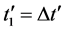
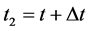
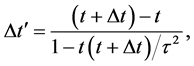
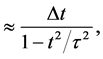
since
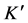
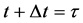
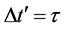

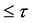
9. Total Cosmic Time Transformation Due to the Expansion of Space and the Additon of Cosmic Times
Combine the two transformations by taking the product of time dilation (62) due to the expansion of the universe with time contraction (69) due to the addition of cosmic times. The total elapsed cosmic time 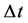
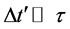

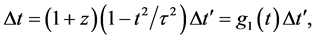
where by substituting for 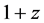
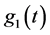
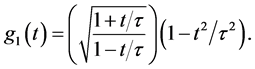
Substituting for 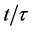

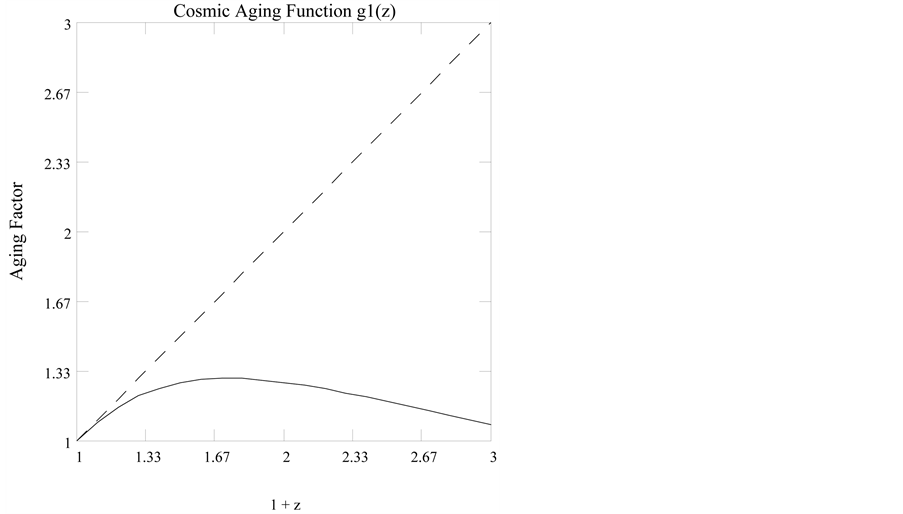
The cosmic aging function 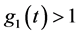
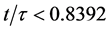
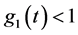
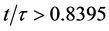
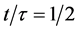
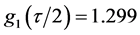
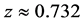
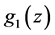
Figure 1. Cosmic aging function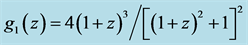

10. Distances
We use the distance relation (23) with the density
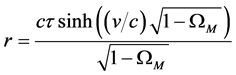
where 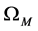
In CGR the luminosity distance relation 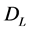
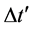
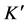
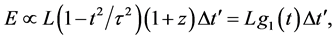
which from (73) is the cosmic aging function 
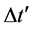
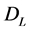

which is a factor 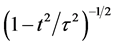
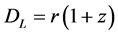
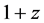
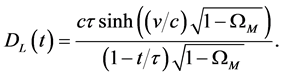
In practice we make the substitution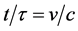
11. Distance Data Fitting
We apply the luminosity distance relation (78) plus a calculated best fit fixed offset 
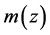
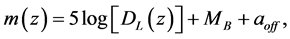
where we apply (58) to convert from 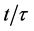
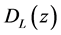
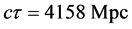
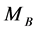
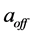
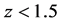

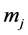
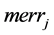
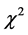
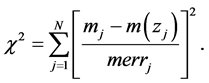
The reduced chi-squared 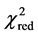
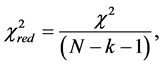
where N is the number of data samples and k is the number of fitting parameters.
For the 
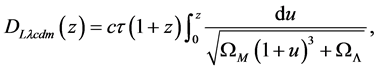
where 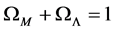
Although SNE-Ia data are independent of any particular cosmology, this is not so for GRB data which must be calibrated with a specified cosmological model. This is because SNE-Ia have nearby sources to use for calibration, but for GRB there are no nearby sources for this purpose. The original GRB data set was calibrated with the 
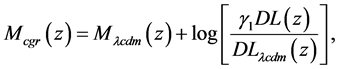
where 
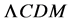

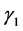
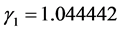
data to form the complete data set. For the CGR model, the number of parameters 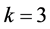
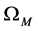

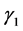
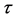
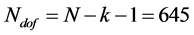



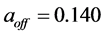
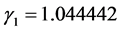

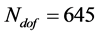
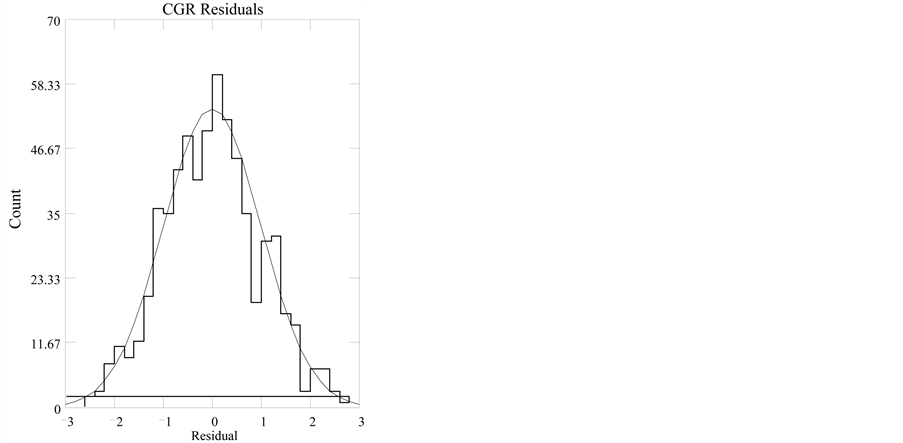
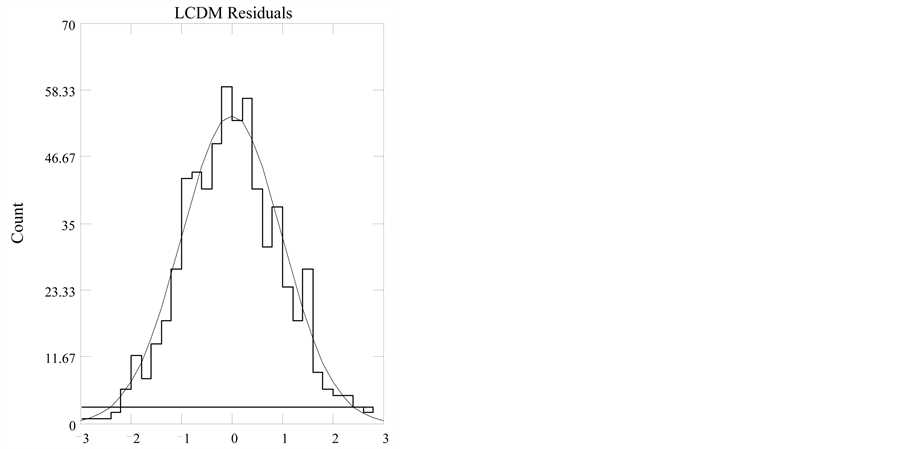
3 shows the histogram of the normalized residual errors for the fit. The solid curve is a Gaussian with mean 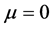

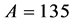
We fit the 
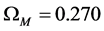
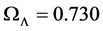
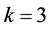


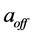
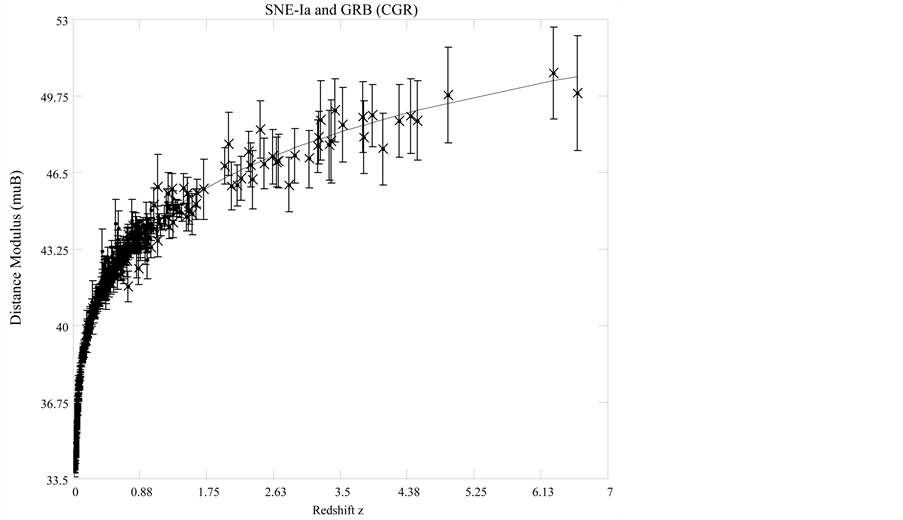
Figure 2. SCP Union 2.1 SNe-Ia data [5] (filled circles) and GRB [6] (dotted x’s). The solid line is for CGR 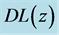
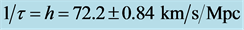
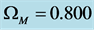
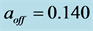


Figure 3. Histogram of CGR residuals 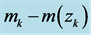
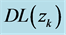
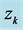
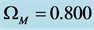
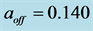

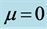
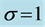
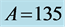
Table 1. CGR vs. 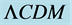
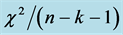
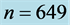

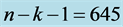

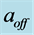
constant of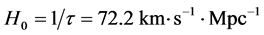
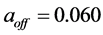
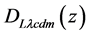
data set. The parameter 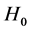
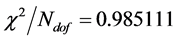
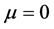
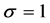
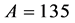
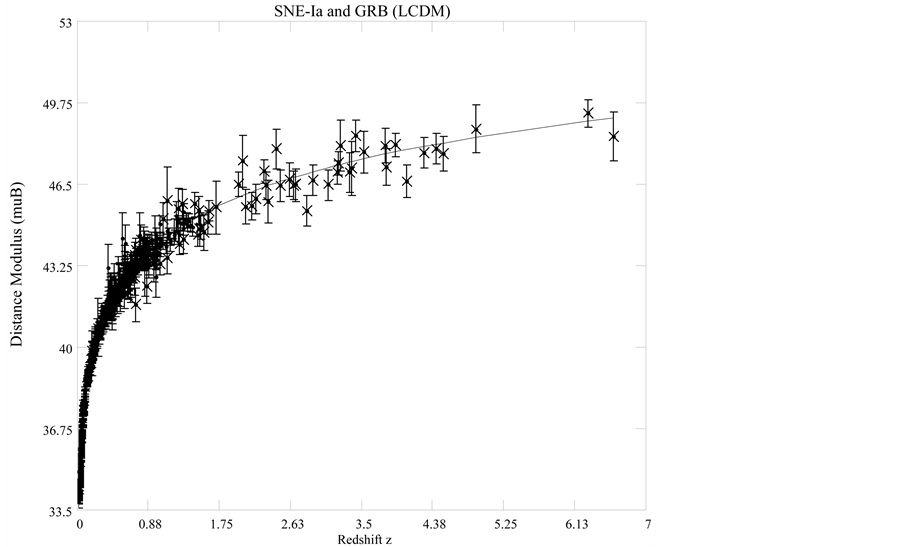
Under the reduced chi-squared statistical model, the ideal reduced 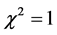
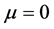
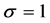

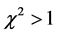
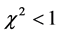
We see that the CGR model under fits the data by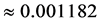
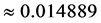
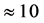

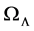

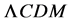
Dark Matter and the X Particle Hypothesis
Assume that the mass density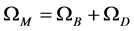

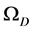
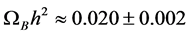
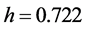
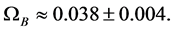
Then, for 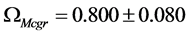

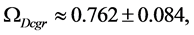
compared to the 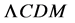
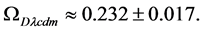
In an extension to the standard model (SM), a hypothetical X particle [8] is theorized to exist, having 2 species, 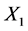
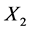
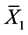

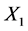
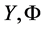

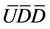
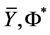
Figure 4. SCP Union 2.1 SNe-Ia data [5] (filled circles) and GRB [6] (dotted x’s). The solid line is for 
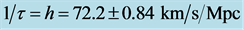


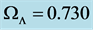
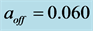

Figure 5. Histogram of 
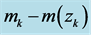

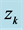
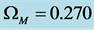
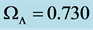
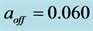
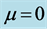

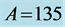
this extended model, is theorized to be composed entirely of hidden particle states (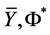
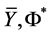

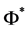
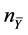
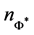
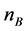
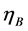
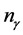
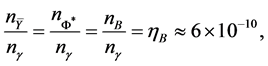
for a baryon density
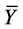
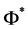
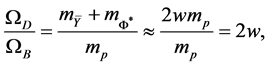
where 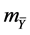
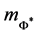
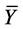


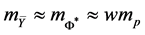
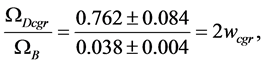
which implies
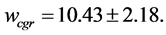
This gives rest mass energies for the 

For the 
which implies
This gives rest mass energies for the 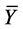
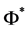
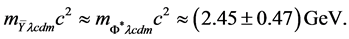
In both cases above we have tried to account for the constraint that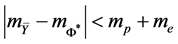

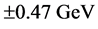
12. Time Dilation in SNe-Ia Light Curves
We now consider two SNe-Ia (SNe) light curve experiments [2] [3] . Common to both experiments is the stretch of the SNe light curve interval for each distant source when compared to the standard nearby (local) source. Because these studies rely on a model for what the light curve looks like in the rest frame of the source SNe, we will require the use of both kinds of cosmic time additions described above. The light curve time interval

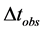

In CSR this is the time interval that is observed from a source light curve or any time varying phenomenon at a cosmic time t in the past.
On the other hand, we can describe the light curve recorded by the observer in the frame 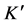
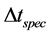


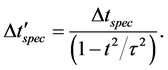
If we make the assumption that
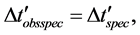
then combining (95) with (97) yields
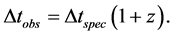
It is evident that CSR, assuming (97), is consistent with the time dilation reports showing effects of cosmic aging equivalent with 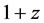

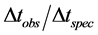
For the SNe data from [2] the light curve agings are given as the light curve width w and the error in the width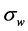
will assume that the equivalent local rest frame time is 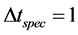
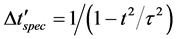
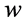

We will use (99) to acquire the redshift z and hence 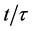

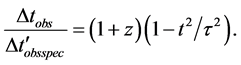
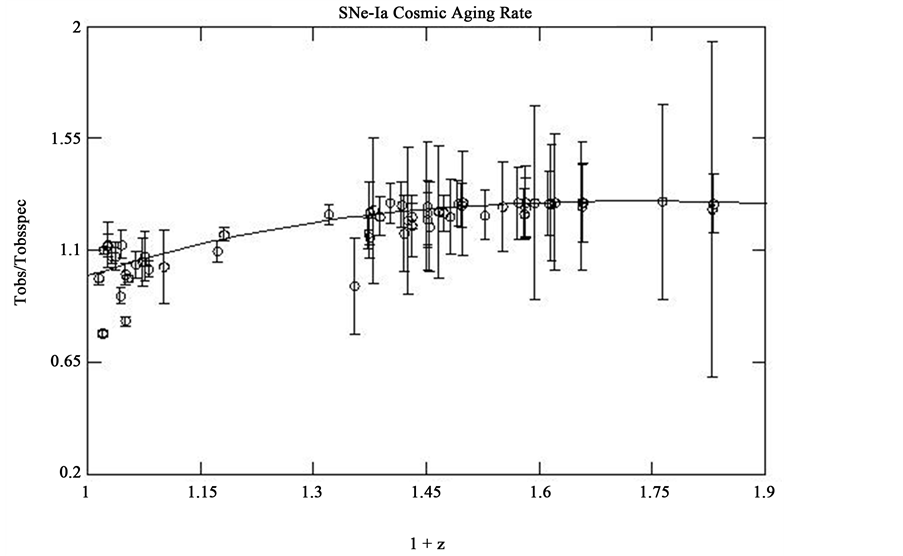
The plotted data are shown in Figure 6. For data points with 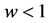
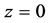
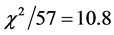
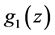
The next SNe data are from [3] . We take the aging rates 
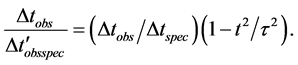
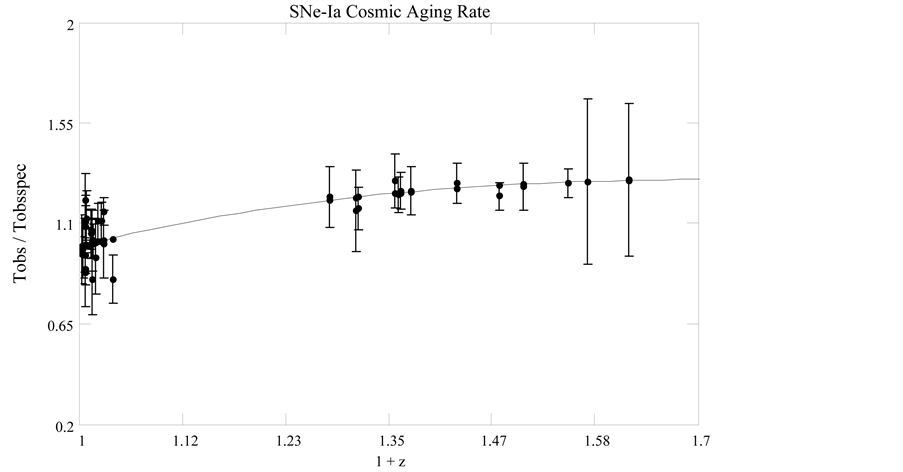
The errors come from [3] (Table 3), in the last column, parenthesized. The redshifts are computed from the aging rate data instead of from the given host galaxy values. The plotted data are shown in Figure 7. Again we note the reduction in the aging rate at higher redshifts. The reduced chi-squared for the data fitted to the cosmic aging rate 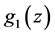
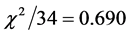
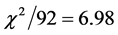
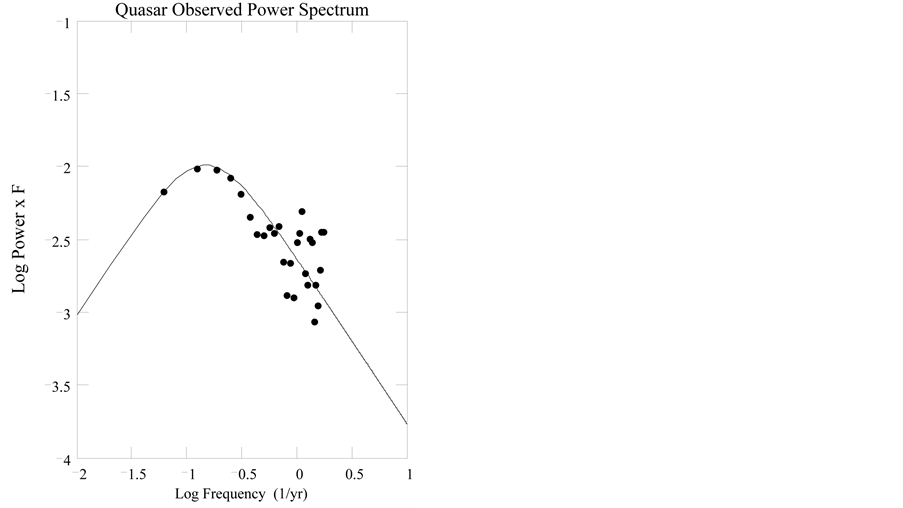
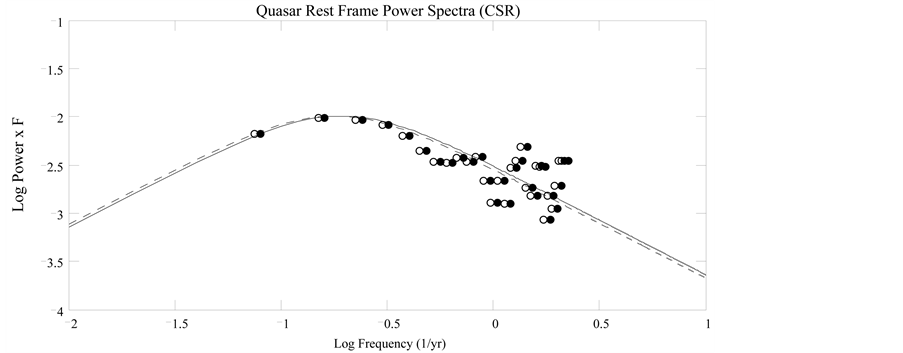
13. Simulation of Quasar Like Light Curve Power Spectra
The purpose of this section is to simulate quasar like light curve power spectra to compare with the report of observed low and high redshift quasar light curve power spectra [1] . The observed light curve power
Figure 6. Calán/Tololo low z and SCP high z SNe-Ia light curve time intervals [2] (Goldhaber, et al.). Open circles are 

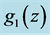
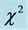
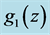
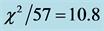
Figure 7. SCP low z and high z SNe-Ia light curve time intervals [3] (Blondin, et al.). Filled circles are 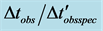
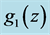
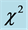

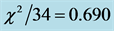
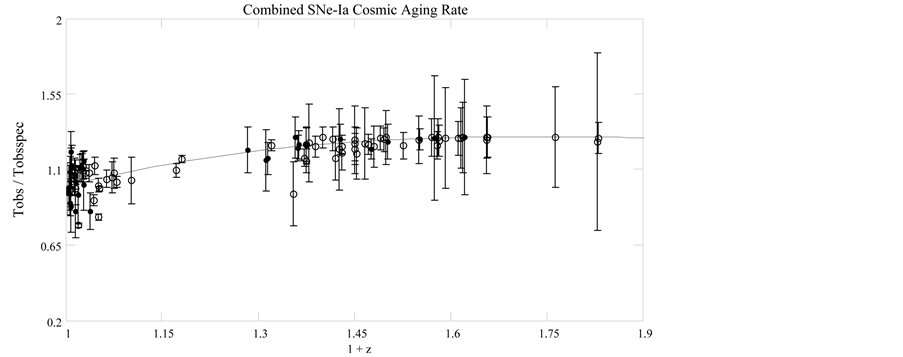
Figure 8. Combined SNe-Ia light curve time intervals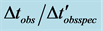
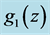
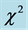
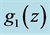
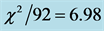
spectra [1] (Figure 5, left-hand panel) were found to be identical within the experimental errors. Therefore, we will assume the low and high redshift light curves are identical in the observer frame K. In addition, it is assumed that the redshifts are of pure cosmological origin, with no components of gravitational redshifts or
Doppler shifts. In our simulation, the pseudo quasar light curve apparent magnitudes 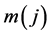
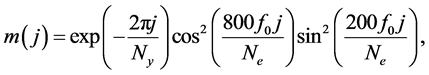
for each epoch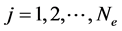

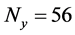
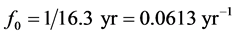
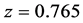
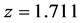
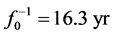
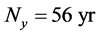
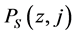
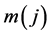

where j runs over 

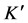
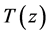
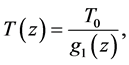
where 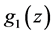
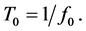
We divide by 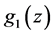
For our purposes, the flat space Friedmann-Lemaître-Robertson-Walker (FLRW) model is the CSR model with the cosmic aging function 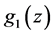

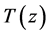
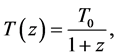
where we have again divided out the time transformation to get to the quasar rest frame.
For either model we use the fitting function 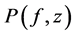

where 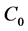
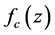

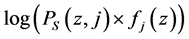
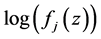
Assuming both quasars have identical power spectra in the observer frame K, we obtain the power spectrum from (103) by setting the redshift 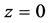
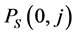

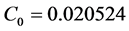
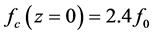


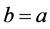
Next we show the light curve power spectra for the low and high redshift quasars, 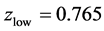
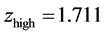
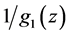
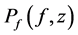
Figure 9. Simulated quasar light curve power spectrum, filled circles, observed at origin of frame K at cosmic time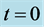

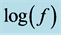

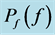


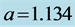
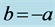
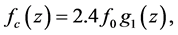
with 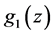
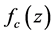
To show what the power spectra might look like for a flat space FLRW observation we show the low and high redshift quasar light curve power spectra when the light curves are corrected for time dilation by

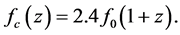
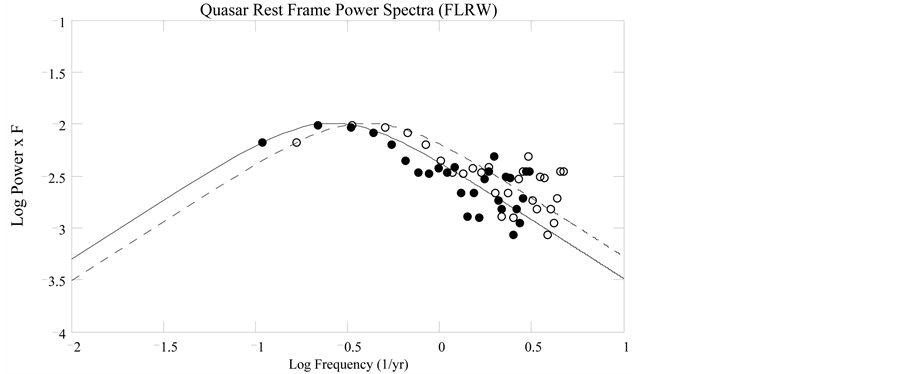
In Figure 12 we show a contour plot of the cosmic aging ratio 
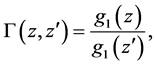
between two source fields, one at redshift z and the other at redshift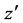
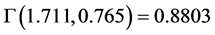
For another demonstration of the cosmic aging ratio, we show in Figure 13 the power spectrum for each quasar in its rest frame where 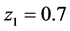
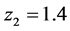
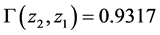
14. CMB Anisotropy Acoustic Peak
In CGR the big bang occurred at velocity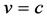
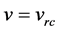
Figure 10. Simulated quasar light curve power spectra in the rest frame 
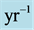


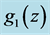
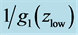

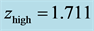
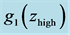

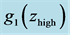
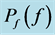

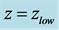
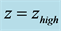
Figure 11. Simulated quasar light curve power spectra in the rest frame 
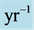
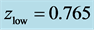

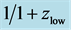
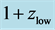
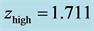



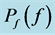

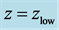

Figure 12. Contour plot of 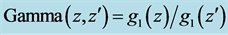
Figure 13. Simulated quasar light curve power spectra in the rest frame 
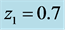
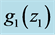
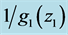
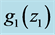
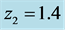
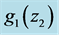
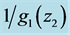
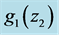
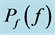

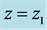
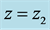
which is related [4] to the time 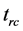
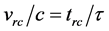
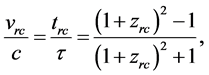
where 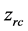
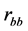
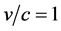
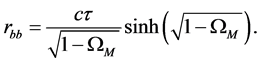
Likewise, the coordinate distance 
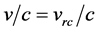
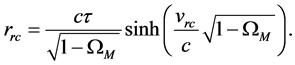
We construct a simple model to determine the size of the sound horizon [16] [17] for the longest sound wave, which generates the first acoustic peak. If 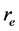
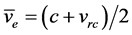
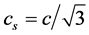
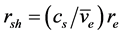
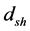
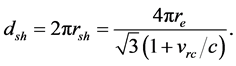
Defining
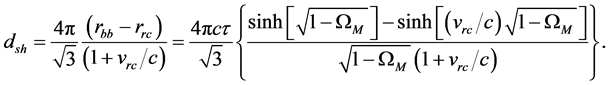
The angle 
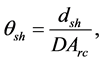
where the angular diameter distance 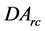
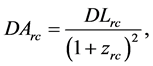
where 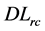

The CMB radiation escaped the matter sphere and expanded to fill all space. The size of the sound horizon 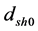
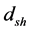
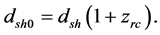
Then, the angle 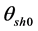
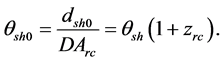
The multipole l of the first acoustic peak [16] recorded in the CMB radiation field is proportional to the inverse of (120),
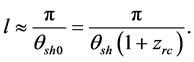
Substituting 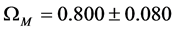

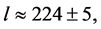
which is in good agreement with observation [18] [19] and,
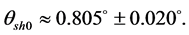
The size of the sound horizon on today’s sky is
15. Discussion
Let us review briefly some aspects of the Carmeli five dimensional brane world cosmological model.
15.1. Velocity, Acceleration and Cosmic Distances in CSR
From (33), for 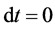
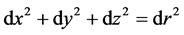
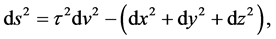
This can be manipulated to obtain
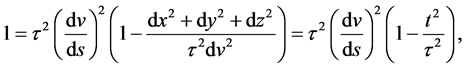
where
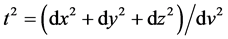
is the cosmic time (squared). Using (125) this gives for the components of the four-velocity in CSR,

where 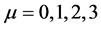
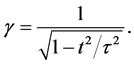
We have from (127) that
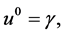
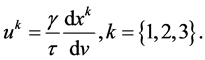
Defining 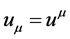
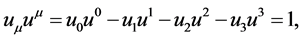
that is, the length of 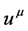
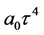

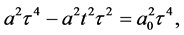
where
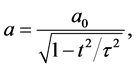
is the acceleration at any cosmic time t. Equation (132) can be put into the form
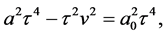
where
is the velocity of a point which had an acceleration a over a time t. Defining the cosmic distance 
where
15.2. Behavior for Large Cosmic Time
The cosmological redshift (57) and the cosmic aging function (74) are two functions which can be used to describe the behaviour expected at large cosmic time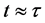
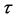
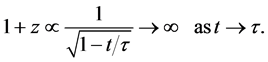
The luminosity distance (78), as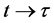
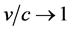
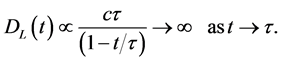
For the standard model, the luminosity distance relation, by (137), 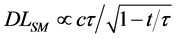
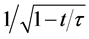
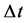
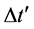
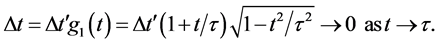
This implies that durations of events, such as for example star formation, star collapse or star bursts, observed in nearby galaxies at cosmic times 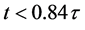
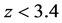
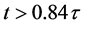
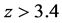
15.3. The Cosmological Redshift vs. the Cosmic Aging Function
One may ask why the cosmological redshift of the wave length 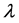
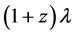
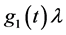
15.4. The Accelerated Expansion
CGR does not have a cosmological constant, but it does have a critical mass density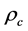

where

is the constant negative mass density of the vacuum, which is not the common view of a vacuum density. Differentiating (18) with respect to v we obtain the acceleration in space-velocity, which we put in the form
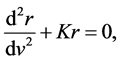
where
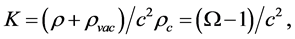
and we have made the substitution, using (141),
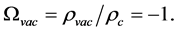
Equation (142) is Hooke’s law of the universe [7, Section 5.4] where K is Hooke’s constant for the universe. If 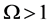
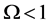
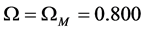
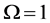
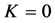
Although beyond the scope of this paper, we give an expression [21] for the vacuum density 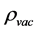
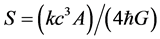
constant, 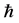

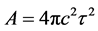


which can be put into the form relating to the vacuum mass density
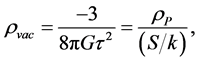
where the cosmological Planck mass density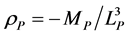
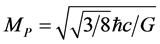
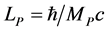

15.5. Gravitational Waves as a Theoretic Selection Criteria
When gravitational waves are detected we will be able to better quantify the strengths and weaknesses of the standard model (GR) and other models. In this regard, a paper on gravitational wave interferometry [23] has a good description of alternative theories to GR and is a fine starting place for further research. Along those lines of inquiry, [24] describes the behaviour of gravitational waves in Carmeli cosmology, predicting a highly attenuated result for gravitational waves from galactic sources but possible detectability for gravitational waves from within the Milky Way Galaxy.
16. Conclusion
In this paper, we used the linearized approximation of the 5-D Cosmological General Relativity as developed by Carmeli. A flat space CSR model was derived in a general way from the curved space CGR model. The CGR luminosity distance relation was applied to SCP Union 2.1 SNe-Ia distance data up to redshift 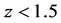

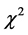
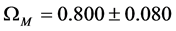
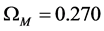
constituents, the CGR model determines rest mass energies for the 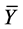


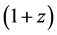



Cite this paper
Firmin J. Oliveira, (2016) Cosmic Time Transformations in Cosmological Relativity. Journal of High Energy Physics, Gravitation and Cosmology,02,253-279. doi: 10.4236/jhepgc.2016.22022
References
- 1. Hawkins, M.R.S. (2010) On Time Dilation in Quasar Light Curves. Monthly Notices of the Royal Astronomical Society, 405, 1940-1946. http://dx.doi.org/10.1111/j.1365-2966.2010.16581.x
- 2. Goldhaber, G., Groom, D.E., Kim, A., Aldering, G., Astier, P., Conley, A., et al. (2001) Timescale Stretch Parameterization of Type Ia Supernova B-Band Light Curves. The Astrophysical Journal, 558, 359-368. http://arxiv.org/abs/astro-ph/0104382 http://dx.doi.org/10.1086/322460
- 3. Blondin, S., Davis, T.M., Krisciunas, K., Schmidt, B.P., Sollerman, J., Wood-Vasey, W.M., et al. (2008) Time Dilation in Type Ia Supernova Spectra at High Redshift. The Astrophysical Journal, 682, 724-736. http://arxiv.org/abs/0804.3595 http://dx.doi.org/10.1086/589568
- 4. Carmeli, M. (2002) Cosmological Special Relativity. Second Edition, World Scientific, Singapore.
- 5. Supernova Cosmology Project. 26 January 2016.
http://www.supernova.lbl.gov/Union/figures/SCPUnion2.1_mu_vs_z.txt - 6. Schaefer, B.E. (2007) The Hubble Diagram to Redshift >6 from 69 Gamma-Ray Bursts. The Astrophysical Journal, 660, 16-46. http://www.arxiv.org/abs/astro-ph/0612285 http://dx.doi.org/10.1086/511742
- 7. Carmeli, M. (2008) Relativity: Modern Large-Scale Spacetime Structure of the Cosmos. World Scientific, Singapore.
- 8. Davoudiasl, H., Morrissey, D.E., Sigurdson, K. and Tulin, S. (2010) Unified Origin for Baryonic Visible Matter and Antibaryonic Dark Matter. Physical Review Letters, 105, Article ID: 211304. http://arxiv.org/abs/1008.2399 http://dx.doi.org/10.1103/physrevlett.105.211304
- 9. Oliveira, F.J. and Hartnett, J.G. (2006) Carmeli’s Cosmology Fits Data for an Accelerating and Decelerating Universe without Dark Matter or Dark Energy. Foundations of Physics Letters, 19, 519-535. http://www.arxiv.org/abs/astro-ph/0603500v4 http://dx.doi.org/10.1007/s10702-006-1007-4
- 10. Hartnett, J.G. and Oliveira, F.J. (2007) Luminosity Distance, Angular Size and Surface Brightness in Cosmological General Relativity. Foundations of Physics, 37, 446-454. http://www.arxiv.org/abs/astro-ph/0603500v5 http://dx.doi.org/10.1007/s10701-007-9108-x
- 11. Greiner, J. (22 December 2015). http://www.mpe.mpg.de/~jcg/grbgen.html
- 12. Weinberg, S. (2008) Cosmology. Oxford University Press, New York.
- 13. Hartnett, J.G. (2008) Extending the Redshift-Distance Relation in Cosmological General Relativity to Higher Redshifts. Foundations of Physics, 38, 201-215.
http://arxiv.org/abs/0705.3097 http://dx.doi.org/10.1007/s10701-007-9198-5 - 14. Oztas, A.M. and Smith, M.L. (2014) The Cosmological Constant Constrained with Union2.1 Supernovae Type Ia Data. International Journal of Theoretical Physics, 53, 2636-2661.
http://www.arxiv.org/abs/1401.0724 http://dx.doi.org/10.1007/s10773-014-2061-5 - 15. Burles, S., Nollett, K.M. and Turner, M.S. (2001) Big-Bang Nucleosynthesis Predictions for Precision Cosmology. The Astrophysical Journal, 552, L1-L5. http://www.arxiv.org/abs/astro-ph/0010171
- 16. Cornish, N.J. (2000) Using the Acoustic Peak to Measure Cosmological Parameters. Physical Review D, 63, Article ID: 027302.
http://www.arxiv.org/abs/astro-ph/0005261 http://dx.doi.org/10.1103/physrevd.63.027302 - 17. 11 January 2016. http://astro.uchicago.edu/~frieman/Courses/A411/Lecture8/Lecture8-2010.pdf
- 18. Hinshaw, G., Weiland, J.L., Hill, R.S., Odegard, N., Larson, D., Bennett, C.L., et al. (2009) Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Data Processing, Sky Maps, and Basic Results. The Astrophysical Journal Supplement Series, 180, 225-245. http://www.arxiv.org/abs/0803.0732 http://dx.doi.org/10.1088/0067-0049/180/2/225
- 19. Hanany, S., Ade, P., Balbi, A., Bock, J., Borrill, J., Boscaleri, A., et al. (2000) MAXIMA-1: A Measurement of the Cosmic Microwave Background Anisotropy on Angular Scales of 10'-5. The Astrophysical Journal Letters, 545, L5- L9. http://www.arxiv.org/abs/astro-ph/0005123
- 20. Carmeli, M. (2001) Velocity, Acceleration and Cosmic Distances in Cosmological Special Relativity. http://www.arxiv.org/abs/astro-ph/0111260
- 21. Oliveira, F.J. (2012) Particle Pair Production in Cosmological General Relativity. International Journal of Theoretical Physics, 51, 3993-4005.
http://www.arxiv.org/abs/1203.4797 http://dx.doi.org/10.1007/s10773-012-1291-7 - 22. Wikipedia: Black Hole Thermodynamics. http://www.wikipedia.org/wiki/Black_hole_thermodynamics
- 23. Corda, C. (2009) Interferometric Detection of Gravitational Waves: the Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282.
http://www.arxiv.org/abs/0905.2502 http://dx.doi.org/10.1142/S0218271809015904 - 24. Hartnett, J.G. and Tobar, M.E. (2006) Properties of Gravitational Waves in Cosmological General Relativity. International Journal of Theoretical Physics, 45, 2181-2190. http://www.arxiv.org/abs/gr-qc/0603067 http://dx.doi.org/10.1007/s10773-006-9181-5