Journal of Biosciences and Medicines
Vol.04 No.05(2016), Article ID:66709,9 pages
10.4236/jbm.2016.45009
Estimated Genetic Variance Explained by Single Nucleotide Polymorphisms of Different Minor Allele Frequencies for Carcass Traits in Japanese Black Cattle
Shinichiro Ogawa1*, Hirokazu Matsuda1, Yukio Taniguchi1, Toshio Watanabe2, Yoshikazu Sugimoto3, Hiroaki Iwaisaki1
1Graduate School of Agriculture, Kyoto University, Kyoto, Japan
2National Livestock Breeding Center, Nishigo, Fukushima, Japan
3Shirakawa Institute of Animal Genetics, Japan Livestock Technology Association, Nishigo, Fukushima, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 April 2016; accepted 21 May 2016; published 24 May 2016
ABSTRACT
Japanese Black cattle are a beef breed and well known to excel in carcass quality, but the details of genetic architectures for carcass traits in beef breeds including this breed are still poorly understood. The objective of this study was to estimate the degree of additive genetic variance explained by single nucleotide polymorphism (SNP) marker groups with different levels of minor allele frequency (MAF) for marbling score and carcass weight in Japanese Black cattle. Phenotypic data on 872 fattened steers with the genotype information about 40,000 autosomal SNPs were analyzed using two different statistical models: one considering only SNPs selected based on MAF (model 1) and the other also considering all remaining SNPs as the different term (model 2). All available SNPs were classified into 10 groups based on their MAFs. For both traits, the estimated proportions of additive genetic variance explained by SNPs selected based on their MAFs using model 1 were always higher than the estimated ones using model 2. For carcass weight, relatively high values of the proportion of the additive genetic variance were estimated when using SNPs with MAFs which were in the ranges of 0.20 to 0.25 and 0.25 to 0.30, which may be partly due to the three previously-reported quantitative trait loci candidate regions. The results could have provided some information on the genetic architecture for the carcass traits in Japanese Black cattle, although its validity may be limited, mainly due to the sample size and the use of simpler statistical models in this study.
Keywords:
Additive Genetic Variance, Carcass Trait, Japanese Black Cattle, Minor Allele Frequency, Single Nucleotide Polymorphism

1. Introduction
Japanese Black cattle are the main breed in the Japanese native cattle, so-called Wagyu. This breed is well known to be a beef one and excel in “shimofuri” in Japanese, or marbling. Degree of marbling and carcass weight are the most economically important carcass traits in this breed. Heritability estimates of 6 representative carcass traits including the two traits in the Japanese population of this breed are moderate to high [1] , which were obtained using pedigree information. For this breed, 3 candidate regions of major gene quantitative trait loci (QTLs) for carcass weight have been reported (called CW-1, CW-2 and CW-3 [2] - [5] ) and Nishimura et al. (2012) [5] suggested that one-third of additive genetic variance for this trait is explained by these 3 QTLs. Ogawa et al. (2014) [6] stated that degree of marbling in this breed is likely to be controlled by only many polygenes. However, the whole genetic architectures for these carcass traits are still poorly understood.
Genomic evaluation (GE) and selection (GS), which were proposed by Meuwissen et al. (2001) [7] , exploit a model including the effects of a large number of genome-wide DNA markers such as high-density single nucleotide polymorphisms (SNPs). The simultaneous use of high-density SNP markers is expected to capture the whole amount of additive genetic variance of the trait of interest, being based on the assumption that each of all QTLs is in the status of linkage disequilibrium (LD) with one or more of those SNPs. When there is fully high LD between a QTL and a SNP, the frequency of a causative allele at the QTL and that of the allele at the SNP are considered to be almost the same. Therefore, SNP markers with different minor allele frequencies (MAFs) may capture a different part of additive genetic variance.
The objective of this study was, using two different statistical models, to investigate the degrees of additive genetic variance explained by genome-wide, high-density SNP marker groups which had different levels of MAF for marbling score and carcass weight in Japanese Black cattle.
2. Materials and Methods
2.1. Ethics Statement
Animal care and use was according to the protocol approved by the Shirakawa Institute of Animal Genetics Animal Care and Use Committee, Nishigo, Japan (ACUCH21-1).
2.2. Phenotypic Data
Marbling scores and cold carcass weights of 872 Japanese Black fattened steers whose ages ranged from 15.3 to 43.0 months were used for the current analyses. These records were collected from 2000 through 2009 at two large carcass markets in Japan, namely Tokyo Metropolitan Central Wholesale Market and Osaka Municipal South Port Wholesale Market. Marbling score is the degree of marbling ranging from null (1) to very abundant (12), assessed on the ribeye of the carcass dissected at the sixth and the seventh rib section, according to the Japan carcass grading standards [8] . Originally, these steers were chosen based on their marbling scores to perform genome-wide association studies. Consequently, while the records of carcass weight followed a bell shape distribution, those of marbling score did a bimodal one which had a peak in the lower and the upper tails each. Mean and standard deviation was 496.6 and 48.0 kg for carcass weight and 6.8 and 3.5 point for marbling score. Pedigree information on the animals was not available in this study.
2.3. Genotype Data
DNA samples of the steers were extracted from perirenal adipose tissues. Sample DNA was quantified and genotyped using the BovineSNP50v1BeadChip. The genotype data on a total of 38,467 autosomal SNPs were used, which had the values of MAFs and genotype call rates larger than 0.01 and 0.95, respectively, and were in Hardy-Weinberg equilibrium (p value > 0.001). Missing genotypes were filled using “BEAGLE 3.3.2” [9] . Figure 1 is a histogram of MAFs of the available 38,467 SNPs after missing genotypes were filled. Based on MAF, all available SNPs were classified into one of ten groups for the current analyses.
2.4. Statistical Analyses
A linear model (denoted as model 1) was used to analyze the data:
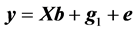 (1)
(1)
where y is the vector of records, b is the vector including overall mean and macro-environmental effects, or discrete effects of carcass markets and years at slaughter and continuous effects of months of age at slaughter (linear and quadratic covariates), 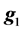 is the vector of genomic breeding values based on the selected n SNPs of animals, or the sums of the additive effects of the selected SNPs, e is the vector of residuals, and X is an incidence matrix relating b with y. When analyzing with model 1, the mean and the variance of y were assumed, as follows:
is the vector of genomic breeding values based on the selected n SNPs of animals, or the sums of the additive effects of the selected SNPs, e is the vector of residuals, and X is an incidence matrix relating b with y. When analyzing with model 1, the mean and the variance of y were assumed, as follows:
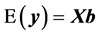 (2)
(2)
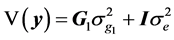 (3)
(3)
where  is the additive genetic variance explained by the n SNPs,
is the additive genetic variance explained by the n SNPs, 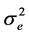 is the residual variance,
is the residual variance, 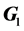 is the genomic relationship matrix (G matrix) among animals which were constructed using the genotype data on the selected n SNPs and I is an identity matrix.
is the genomic relationship matrix (G matrix) among animals which were constructed using the genotype data on the selected n SNPs and I is an identity matrix.
The data were also analyzed using a following linear model (model 2):
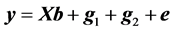 (4)
(4)
where 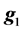 is as defined in model 1 and
is as defined in model 1 and  is the vector of genomic breeding values based on the “remaining SNPs”, or the (38,467 − n) SNPs. The mean and the variance of y were assumed, as follows:
is the vector of genomic breeding values based on the “remaining SNPs”, or the (38,467 − n) SNPs. The mean and the variance of y were assumed, as follows:
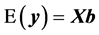 (5)
(5)
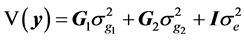 (6)
(6)
where 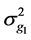 and
and  are defined as in model 1,
are defined as in model 1,  is the additive genetic variance captured by the (38,467 − n) SNPs,
is the additive genetic variance captured by the (38,467 − n) SNPs, 
Figure 1. Histogram of minor allele frequencies of all SNPs available in this study.
According to VanRaden (2008) [10] , the G matrix 

where 





Correlation coefficients were calculated between the elements of 


All the parameters in the two models were estimated via the Bayesian framework using Gibbs sampling in “BLR” package under R environment [11] [12] . In the analyses, the term 










The 


computing, from each sample, the value of 





Posterior probability densities of the variance components were computed with the R function “density” using samples obtained, and the estimated 

For both traits, 






3. Results and Discussion
Results of correlation and single regression for the elements of the two different G matrices are shown in Table 1. For diagonal elements, the value of correlation coefficient was 0.94 and highest when selecting the SNP groups with MAF bins of 0.20 - 0.25 and 0.25 - 0.30 and became lower when selecting SNPs with MAFs higher than 0.30 or lower than 0.20. The value of single regression coefficient was increased monotonically from 0.61 when selecting SNPs with MAFs in a MAF bin of 0.45 - 0.50 to 3.66 when selecting SNPs with MAFs in a MAF bin of 0 - 0.05. For upper-triangular elements, correlation coefficients were around 0.96 and relatively high when selecting the SNP groups with MAF bins of 0.15 - 0.20 to 0.45 - 0.50. Single regression coefficients were approximately around 1, or 0.99 to 1.06, and relatively high for the SNP groups with MAF bins of 0.15 - 0.20 to 0.45 - 0.50. These results could be mainly due to the distribution of SNP genotypes in the current population and may indicate the possibility of SNPs in different MAF groups to capture a different part of additive genetic variance for a given trait.
Table 1. Correlation and single regression coefficients for the elements of genomic relationship matrix constructed using all available SNPs and those constructed using selected SNPs based on their minor allele frequencies (MAFs).
Figure 2 illustrates the estimates of 



When model 2 was used, the estimated 















For both traits, the estimates of 

In this study, the frequencies corresponding alleles of SNPs in the chip associated with CW-1 and CW-2 were 0.799 and 0.229, respectively. So these two SNPs were the SNPs in the MAF range of 0.20 to 0.25, giving a high possibility that the additive genetic variance due to the two regions, CW-1 and CW-2, was captured by using the SNPs in MAF range of 0.20 to 0.25. Therefore, why relatively high values of 
Figure 2. Changes in estimates of 


Figure 3 and Figure 4 show the changes in the correlation and regression coefficients, comparing 








Using the genotype data of high-density SNPs and fitting the model similar to model 2, Abdollahi-Arpanahi et al. (2014) [13] studied how markers with different MAFs differ in their abilities to explain additive genetic variability for three production traits in chicken. Then, they stated that it was difficult to draw clear conclusion from the obtained results, which was a setting similar to the current study. While it was assumed with model 2 that there was no covariance structure between the selected and the remaining SNPs, there may be the possibility to exist the high degree of LDs between the SNPs used to construct 




Figure 3. Changes in correlation coefficients between the elements of 





tween SNPs of different MAF groups, and in such a situation, using model 2 could give less plausible results. A smaller sample population size often causes a spurious LD structure in the population, which would make the interpretation of the results more difficult. This problem could be mitigated by using more samples.
In this study, for both traits, the estimated proportions of additive genetic variance explained by SNPs selected based on their MAFs using model 1 were always higher than the estimated ones using model 2. For carcass weight, relatively high values of the proportion of the additive genetic variance were estimated when using SNPs with MAFs which were in the ranges of 0.20 to 0.25 and 0.25 to 0.30, which may be partly due to two of three previously-reported QTL candidate regions. The results could have provided some information on the genetic architecture for the carcass traits in Japanese Black cattle, although its validity may be limited, mainly due to the sample size and the use of simpler statistical models in this study. There will be other sources to characterize each of SNP markers (e.g., genome position information, gene function information and so on), and then these could give a chance to analyze with a different way to partition all available SNPs.
4. Conclusion
In this study, for marbling score and carcass weight in the Japanese Black cattle population, we tried to partition
Figure 4. Changes in regression coefficients where the values of the independent variable were the elements of 





the additive genetic variances captured by genome-wide SNP markers into two different components, based on the information on their MAFs. Results indicated that the whole additive genetic variance captured by all available SNPs could be separately estimated as the two components. Using SNPs in different MAF ranges might explain different parts of the additive genetic variance for the carcass traits. For carcass weight, relatively high values of the proportion of the additive genetic variance were estimated when using SNPs with MAFs which were in the ranges of 0.20 to 0.25 and 0.25 to 0.30, which may be partly due to two of three previously-reported QTL candidate regions. The validity of the findings in this study is definitely necessary to examine using relevant more data and a more sophisticated statistical method.
Acknowledgements
The authors thank the staff of the Shirakawa Institute of Animal Genetics for technical assistance. The work was partly supported by the Ministry of Agriculture, Forestry, and Fishery, Japan, and by the Japan Racing and Livestock Promotion Foundation (H20-5).
Cite this paper
Shinichiro Ogawa,Hirokazu Matsuda,Yukio Taniguchi,Toshio Watanabe,Yoshikazu Sugimoto,Hiroaki Iwaisaki, (2016) Estimated Genetic Variance Explained by Single Nucleotide Polymorphisms of Different Minor Allele Frequencies for Carcass Traits in Japanese Black Cattle. Journal of Biosciences and Medicines,04,89-97. doi: 10.4236/jbm.2016.45009
References
- 1. Oyama, K. (2011) Genetic Variability of Wagyu Cattle Estimated by Statistical Approaches. Animal Science Journal, 82, 367-373.
http://dx.doi.org/10.1111/j.1740-0929.2011.00895.x - 2. Mizoshita, K., Watanabe, T., Hayashi, H., Kubota, C., Yamakuchi, H., Todoroki, J. and Sugimoto, Y. (2004) Quantitative Trait Loci Analysis for Growth and Carcass Traits in a Half-Sib Family of Purebred Japanese Black (Wagyu) Cattle. Journal of Animal Science, 82, 3415-3420.
- 3. Takasuga, A., Watanabe, T., Mizoguchi, Y., Hirano, T., Ihara, N., Takano, A., Yokouchi, K., Fujikawa, A., Chiba, K., Kobayashi, N.,Tatsuda, K., Oe, T., Furukawa-Abe, A., Fujita, T., Inoue, K., Mizoshita, K., Ogino, A. and Sugimoto, Y. (2007) Identification of Bovine QTL for Growth and Carcass Traits in Japanese Black Cattle by Replication and Iddentical-by-Desceny Mapping. Mammalian Genome, 18, 125-136.
http://dx.doi.org/10.1007/s00335-006-0096-5 - 4. Setoguchi, K., Furuta, M., Hirano, T., Nagao, T., Watanabe, T., Sugimoto, Y. and Takasuga, A. (2009) Cross-Breed Comparisons Identified a Critical 591-kb Region for Bovine Carcass Weight QTL (CW-2) on Chromosome 6 and the Ile-442-Met Substitution in NCAPG as a Positional Candidate. BMC Genetics, 10, 43.
http://dx.doi.org/10.1186/1471-2156-10-43 - 5. Nishimura, S., Watanabe, T., Mizoshita, K., Tatsuda, K., Fujita, T., Watanabe, N., Sugimoto, Y. and Takasuga, A. (2012) Genome-Wide Association Study Identified Three Major QTL for Carcass Weight Including the PLAG1-CHCHD7QTL for Stature in Japanese Black Cattle. BMC Genetics, 13, 40.
http://dx.doi.org/10.1186/1471-2156-13-40 - 6. Ogawa, S., Matsuda, H., Taniguchi, Y., Watanabe, T., Nishimura, S., Sugimoto, Y. and Iwaisaki, H. (2014) Effects of Single Nucleotide Polymorphism Marker Density on Degree of Genetic Variance Explained and Genomic Evaluation for Carcass Traits in Japanese Black Beef Cattle. BMC Genetics, 15, 15.
http://dx.doi.org/10.1186/1471-2156-15-15 - 7. Meuwissen, T.H.E., Hayes, B.J. and Goddard M.E. (2001) Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics, 157, 1819-1829.
- 8. Japan Meat Grading Association (JMGA) (1988) New Beef Carcass Grading Standards. JMGA, Tokyo.
- 9. Browning, S.R. and Browning, B.L. (2007) Rapid and Accurate Haplotype Phasing and Missing Data Inference for Whole Genome Association Studies by Use of Localized Haplotype Clustering. The American Journal of Human Genetics, 81, 1084-1097.
http://dx.doi.org/10.1086/521987 - 10. VanRaden, P.M. (2008) Efficient Methods to Compute Genomic Predictions. Journal of Dairy Science, 91, 4414-4423.
http://dx.doi.org/10.3168/jds.2007-0980 - 11. De los Campos, G., Naya, H., Gianola, D., Crossa, J., Legarra, A., Manfredi, E., Weigel, K. and Cotes, J.M. (2009) Predicting Quantitative Traits with Regression Models for Dense Molecular Markers and Pedigree. Genetics, 182, 375-385.
http://dx.doi.org/10.1534/genetics.109.101501 - 12. R Development Core Team (2011) R: A Language and Environment for Statistical Computing. R Development Core Team, Vienna.
- 13. Abdollahi-Arpanahi, R., Pakdel, A., Nejatijavaremi, A., Moradi Shahrbabak, M., Morota, G., Valente, B.D., Kranis, A., Rosa, G.J.M. and Gianola, D. (2014) Dissection of Additive Genetic Variability for Quantitative Traits in Chickens Using SNP Markers. Journal of Animal Breeding and Genetics, 131, 183-193.
http://dx.doi.org/10.1111/jbg.12079
NOTES
*Corresponding author.







