Open Journal of Civil Engineering
Vol.07 No.01(2017), Article ID:74988,24 pages
10.4236/ojce.2017.71009
Evaluation of Guardrail Posts Installed in Asphalt Mow Strips by Static Finite Element Simulation
Esmaeel Bakhtiary, Seo-Hun Lee, David W. Scott, Lauren K. Stewart, Donald W. White
School of Civil and Environmental Engineering, Georgia Institute of Technology, Atlanta, USA

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 8, 2016; Accepted: March 27, 2017; Published: March 30, 2017
ABSTRACT
Asphalt mow strips are typically used as vegetation barriers around guardrail posts in the design of roadside safety structures. Asphalt mow strips have historically been modeled as a rigid layer in simulations; this assumption results in significant ground level restraint on the guardrail post. However, experiments have shown that asphalt rupture should be considered in the analysis of the response of guardrail posts embedded in mow strips. The present study investigates the effect of asphalt material properties and mow strip geometry on guardrail post performance using finite element simulations. Numerical simulations are performed and correlated with results from static experiments and material testing. The test simulations and experimental results are used to evaluate the response of guardrail posts with various mow strip designs to predict the level of restraint from the asphalt layer. The model is then used to investigate the effects of asphalt material properties and mow strip geometry on the overall performance of the system. The results demonstrate that including asphalt rupture in numerical simulations is essential in accurately predicting the behavior of guardrail posts installed in asphalt mow strips. In addition, mow strip geometry along with asphalt material properties significantly affect the guardrail post response.
Keywords:
Guardrail Posts, Asphalt Mow Strips, LS-DYNA, Finite Element Simulations, Roadway Safety

1. Introduction
Considerable research has been performed with testing and finite element simulation of guardrail posts and systems [1] - [6] . Several studies have focused on the soil modeling and its interaction with the guardrail posts. Dewey et al. [7] studied the soil-structure interaction behavior of highway guardrail posts using simplified models. Ferdous et al. [8] used non-linear finite element simulations considering soil modeled as a Joint-Rock material model. Plaxico et al. [9] performed finite element analysis of timber guardrail posts and post-soil interaction. In this study, the post-soil interaction was modeled using the subgrade reaction approach, which involves an array of nonlinear springs attached along the length of the post below grade. Wu et al. [10] studied the interaction between a guardrail post and soil during quasi-static and dynamic bogie vehicle testing. This study employed the methodology of using static testing to plan dynamic testing. According to the measured data, the dynamic resistance of the standard post and soil was about twice that of the quasi-static resistance.
Asphalt mow strips are pavement layers installed around guardrail posts as vegetation barriers. The word asphalt used in this paper refers to asphalt concrete. Without mow strips, regular vegetation control around guardrails such as mowing or herbicide application is required. A common procedure for steel guardrail installation in asphalt mow strips employs a hydraulic machine to drive the posts through a layer of asphalt mow strip. A schematic of an installed post is shown in Figure 1.
Prior research [11] has concluded that asphalt mow strips increase the ground- level restraint of guardrail posts significantly. Therefore, the American Association of State Highway and Transportation Officials (AASHTO) Roadside Design Guide [12] classifies mow strips as rigid foundations and states that guardrail posts in mow strips are not able to rotate in the soil. Further research on the performance of guardrail systems with concrete mow strips was done by Dusty et al. [13] . In the finite element models developed in these studies:
・ The extent of the domain meshed was near the zone of influence of the loaded posts, which implies that boundary effects could potentially influence the results.
Figure 1. Typical guardrail post installation with an asphalt mow strip.
・ The asphalt mow strip was modeled as a rigid layer; the rupture of the asphalt layer was not modeled.
Asphalt mow strips assumed as a rigid layer cause significant ground level restraint of guardrail posts in simulations. However, experiments have shown that asphalt deforms and ruptures when lateral loads are applied to guardrail posts installed in asphalt mow strips [14] . Because asphalt rupture and other attributes of the asphalt response significantly affect system performance, the asphalt behavior must be considered in test simulations and an effective way to model guardrail post systems including asphalt mow strips is needed. This model allows investigation of the effect of mow strip geometric design and asphalt material properties on the guardrail post behavior.
In the work presented herein, an experimental program was carried out at an outdoor test site. Guardrail posts were installed in asphalt mow strips subjected to static loading. Results from the tests demonstrated that the performance of the post was affected significantly by mow strip geometry (thickness and rear distance, see Figure 1) [15] . In parallel with the experimental program, three- dimensional (3D) finite element (FE) models were developed. The Mohr-Cou- lomb material model was used to model the behavior of the asphalt, and asphalt rupture was captured using element erosion. The model was refined using the experimental results from material testing as well as the quasi-static test program. Results from the static experimental program and finite element analyses were used to evaluate the performance of the various post/mow strip configurations tested. Parametric studies were performed on different pre-cutting designs, and the effect of asphalt material properties and geometry of the mow strips on the overall system behavior was investigated.
The aim of this paper is to provide a better understanding of the use of numerical simulation to model the behavior of posts restrained by an asphalt layer at the ground line. Static loading is employed in these studies to allow for more extensive evaluation of parameters to design and focus future dynamic tests. Future experiments will be performed to evaluate the performance of individual posts installed in a variety of mow strip configurations under dynamic loading. In addition, pertinent properties will also be evaluated via dynamic material testing. The dynamic material test results will be compared to applicable nondestructive assessments of dynamic properties (such as dynamic modulus). These results from the dynamic subcomponent and material tests will be used to refine the finite element models developed for more detailed parametric analysis of the influence of geometric and material properties of the mow strip on the expected performance of the mow strip. The final phase of the research effort will be MASH compliant full-scale crash testing on selected guardrail-mow strip installations to determine whether systems installed without leave-outs can perform satisfactorily.
2. Experimental Program
The outdoor test site for the experimental program was constructed in accordance with American Association of State Highway and Transportation Officials Manual for Assessing Safety Hardware (MASH) criteria [16] . As directed by the MASH guidelines, the aggregate base material was standardized and compacted to exceed 95% of the maximum dry density of soil for each test configuration. In each test with a mow strip, a Hot Mixed Asphalt (HMA) layer of PG 76-22 binder and 19 mm aggregate size was installed to a specified thickness. Approximately one week after the asphalt installation, W150x13 steel guardrail posts were driven through the asphalt layer and into the ground with a hydraulic post driver. The posts were placed at a specified rear distance from the asphalt edge and were driven to the standard embedment depth of 1,000 mm.
A schematic illustration of the experimental setup including the loading fixture and instrumentation is given in Figure 2. During each test, a hydraulic cylinder was used to apply a lateral load on the guardrail post at a rate of approximately 1 mm/s. A reaction block prevented lateral movement, forcing the post to displace toward the block as the cylinder retracted. An S-type load cell was connected from the hydraulic cylinder to the post via a loading bracket system. Two string potentiometers were mounted on a reference pole to measure lateral displacement at the load point (625 mm above ground level) and at the ground level. To minimize the discrepancy between the inclined distance and actual horizontal distance, the reference pole was located a distance of approximately 1.8 m from the post. A computer-controlled data acquisition system was used to measure and record the laterally applied load and displacements. A detailed description of the experimental program and static test results is given in [15] .
3. Finite Element Model
3.1. Overview of Modeling Techniques
The interactions between the soil, asphalt, and post play a vital role in the response of the system during loading. These interactions can be investigated by first considering the post to be a specialized form of a laterally loaded pile. There are various techniques for solving laterally loaded pile problems. These approaches include: (1) the finite element approach, in which the post is embedded in a soil continuum of solid finite elements, and (2) the subgrade reaction approach, in which the post is supported by a series of uncoupled springs. The
Figure 2. Schematic and a photo of the experimental setup used for quasi-static loading of guardrail posts.
subgrade reaction method has been used widely in the past because of the high computational cost associated with 3D finite element modeling of the soil around the guardrail post. Although the subgrade reaction approach can be used to analyze post-soil interaction, this method only provides an overall performance assessment and does not provide insight into the failure and deformation mechanisms of the soil and possible asphalt layers. With recent advances in computing speeds, researchers have made efforts to model the post-soil interaction using the finite element method. With this approach, models are constructed of the post embedded in a continuum of soil modeled using three-dimensional solid elements. Simulations of physical responses using 3D finite element analysis (FEA) can be readily produced, and the availability of sophisticated FEA tools provides substantial promise for detailed numerical studies to address outstanding questions of the post-soil behavior. However, the quality of the results from simulations depends on several factors including:
・ Accurate representation of geometry details, boundary conditions, and assumed initial conditions.
・ The constitutive relationships for the various materials such as loss of strength in the soil and asphalt under large deformations, asphalt material properties, and the rupture of asphalt.
・ The contact conditions between various components such as the contact between the soil and the post as well as the asphalt layer and the soil.
3.2. Model Domain
LS-DYNA V971 R8.0.0 [17] is used in this research. The quasi-static problem is solved with an explicit algorithm instead of implicit. The model developed in this paper, when updated to incorporate effects associated with dynamic loading, will be used for dynamic impact loading in the next phase of the project. Furthermore, it is anticipated that this model may be utilized more broadly to perform dynamic crash testing. Therefore, optimizing the model for implicit integration is not useful. Moreover, the Mohr-Coulomb material model in LS- DYNA, which is used to model soil and asphalt does not support an implicit solution algorithm for analysis at large strains, and the contact algorithms are less robust with implicit time integration.
The soil domain considered in the model is a rectangular prism. The bottom boundary of the prism is fixed at depth (z-direction) of 2 m―approximately twice the embedment depth. For the lateral boundaries, there are three options to use: free, rigid, or non-reflecting boundary conditions. The lateral boundaries are placed far enough from the post that the displacements and change in stresses at the boundaries are negligible. Therefore, the response is insensitive to the lateral boundary assumptions. For the pseudo-static loading employed in this study, the non-reflecting boundary conditions are effectively the same as the free boundary conditions. Therefore, using any of these three boundary conditions gives similar results. However, because explicit integration is employed, using a non-reflecting boundary decreases noise in the system response and thus the lateral soil boundary is modelled using non-reflecting boundary conditions. Three different criteria are used to determine the size of the prism within the plan of the problem to avoid boundary effects:
1) The size of the prism in plan is increased, and the force-displacement curve for the post is monitored. The results show that the boundary effects on the post’s response vanish when the planar size of the soil is larger than 4 m, and the force-displacement curve is effectively unchanged when using greater than this size.
2) The nodes on the lateral boundary are initially set free. The size of the prism in plan is increased until the displacements of the nodes at the boundaries are less than one percent of the ground level displacement of the steel post. The dimension of the prism in plan is obtained as 5 m by this approach. Then the lateral boundaries are modelled using non-reflecting boundary conditions.
3) The width of the model (perpendicular to the post lateral movement) has to be large enough to capture asphalt rupture. The width is increased until the boundaries are far from the end of asphalt rupture and shear stress at the boundaries is less than 1 percent of shear stress close to the post. The size of the model in this direction is determined equal to 10 m.
Therefore, the dimensions of the prism are set as 5 m in the y-direction (parallel to the post lateral movement) and 10 m in the x-direction (perpendicular to the post lateral movement). The steel post is a W150x13 member with a total length of 1.83 m and an embedded depth of 1 m [12] . The FE model is comprised of approximately 250,000 solid elements for the soil and asphalt and 1,000 shell elements for the steel post. A representation of the model is shown in Figure 3. Other attributes of the finite element mesh and model are discussed below.
3.3. Post and Soil Interface
Various approaches exist for modeling the interface between the soil and post using a Lagrangian mesh:
1) Nodes from the soil elements are tied to the nodes of the post elements. No contact definition between the post and the soil is necessary when this approach
Figure 3. Finite element model of guardrail post, soil and asphalt system in LS-DYNA.
is used. This method assumes infinite friction between the soil and the post, which is not a correct physical representation. This approach yields a stiffer behavior than reality and is not recommended.
2) Nodes from the soil elements are not tied to the nodes of the post elements, and eroding contact is used to simulate the soil failure. When elements are eroded based on specific failure criteria, they are removed from calculations in the model and do not have resistance anymore. This model demands a very dense mesh and can yield incorrect results. The failed elements are removed from the analysis, and a gap is created between the soil and the post. Therefore, application of a relatively small force in the axial direction can pull out the post. This behavior is observed even using a friction coefficient larger than one [18] .
3) Nodes from the soil elements are not tied to the nodes of the post elements. Automatic surface-to-surface contact which is explained further below is defined between the post and the soil. In this method, the friction between the post and soil has an influence on the behavior [18] .
The contact search algorithms utilized by automatic contacts in LS-DYNA make them better-suited than older contact types. Moreover, subroutines that check the slave nodes for penetration are utilized a second time to check the master nodes for penetration through the slave segments in this approach. The definition of the slave surface and master surface is arbitrary. Therefore, in this study, the contacts between soil and steel post are modeled using the automatic surface-to-surface contact model. Static and dynamic friction coefficients are set equal to 0.6, which is typical for an interface between the soil (a mixture of gravel, sand, and clay) and a driven smooth steel pile [19] . The segment-based contact algorithm (SOFT 2) in LS-DYNA checks for segments versus segments penetration instead of nodes versus segments used in default penalty contact formulation. Therefore, it is unlikely for nodes to penetrate undetected as can happen with the standard penalty contact when nodes slip between segments at corners. Because the stiffness of steel is significantly greater than the stiffness of the soil and because of the edges of the steel post, the segment-based contact is used to avoid contact related problems and element penetration. The thickness of the shell elements modeling the steel post is considered with the modeling of the contact with the soil around the post to avoid initial element penetrations. FRCENG (frictional contact energy), the LS-DYNA parameter for frictional energy, is set to 1 to enable sliding energy calculations. The frictional energy is important because a portion of the energy during steel post movement in the soil is dissipated by friction. This energy is verified as a positive value; negative sliding energy is an indication of an erroneous sliding condition between two contact surfaces.
3.4. Asphalt Interfaces
In addition to the contact between the post and the soil, the contact between the asphalt and the soil and the asphalt and the steel is also modeled using the automatic surface-to-surface contact model. The static coefficient of friction is set to a relatively high value of 1.0 to account for the bitumen in the asphalt that is bonded to the soil surface. However, after this connection breaks and the asphalt layer starts to slip over the soil, friction substantially decreases. The kinetic coefficient of friction is assumed to be negligible and is set equal to zero to avoid large forces at the free edge of the asphalt behind the post. This allows the asphalt to move easily on the soil, as observed in the experiments and avoids mesh distortions at the edge of the asphalt layer where there is no confining pressure. Segment based (SOFT 2) contact also is used in this part of the model.
3.5. Mesh Treatments for the Asphalt Layer
When the rupture failure pattern propagates in the asphalt, the tip of the rupture moves from the edges of the post toward the sides of the asphalt layer (Figure 4). Therefore, it is not sufficient to refine the mesh only in the local region around the post. The mesh must be refined for the whole area covering the rupture. Therefore, the mesh around the post is composed of small tetrahedral elements and larger hexahedral elements are used at further distances from the post where rupture is not occurring. Using these larger hexahedral elements reduces computational time significantly and more accurately models the rupture conditions via the use of tetrahedral elements. A tied surface-to-surface contact model is employed in LS-DYNA to tie the surfaces of the different regions to each other in the model. In tied contact types, the slave nodes are constrained to move with the master surface which enables for mesh transition between two different types of elements. The nearest master segment for each slave node is located based on an orthogonal projection of the slave node to the master segment. The two meshes for the asphalt are connected to make a continuum of asphalt using the tied surface-to-surface contact model. Figure 5 shows the mesh transition used for the asphalt layer.
Figure 4. Asphalt rupture observed in the experimental program.
Figure 5. Mesh treatments used for the asphalt layer combining hexahedral and tetrahedral elements.
3.6. Hourglass and Kinetic Energy
Hourglass control number 9 is an enhanced assumed strain stiffness formulation for three-dimensional hexahedral elements. To prevent high hourglass energy during simulations, this hourglass control is used for the soil elements and the hexahedral mesh part of the asphalt. The steel post and tetrahedral mesh portion of the asphalt are modeled as fully integrated elements and do not require an hourglass control. For each analysis, the hourglass energy is monitored and compared to the internal energy. The hourglass energy in the soil and the hexahedral mesh portion of the asphalt is limited to approximately 3 percent of the internal energy, which was deemed acceptable. Kinetic energy is less than 0.5 percent of the total energy in the current simulations, which indicates that the rate of loading is a good representation of quasi-static loading.
3.7. Importance of Gravity Loading
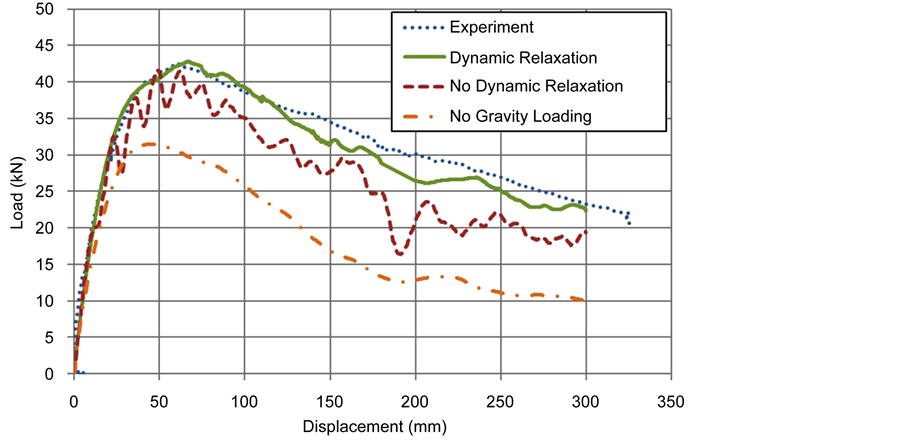
Soil is often a pressure dependent material. Therefore, the soil behavior changes at different depths because of the change in the pressure as the depth increases. To capture this important aspect, gravity loading must be applied, and stresses must be initialized before the start of the main simulation. This is accomplished in this research by applying a “load body” in the z direction to all parts of the model. Because applying gravity loading during real-time simulation causes dynamic waves that can contaminate the results, the gravity load is applied in the pseudo-time before the main simulation. Gravity loading is applied using a ramp load to minimize dynamic waves, and dynamic relaxation is utilized in the pseudo-time to dampen the waves caused by applying gravity. After the waves are damped, and the material reaches a static equilibrium, the main simulation is conducted in real-time. Applying the gravity load also ensures the proper representation of friction forces on the surfaces that are in contact with each other. As can be seen in Figure 6, applying gravity and using dynamic relaxation is critical to model the guardrail post system properly. For the experiment and for gravity loading with dynamic relaxation, the peak force occurs at 70 mm. If the gravity
Figure 6. Comparing the load-displacement curve with and without dynamic relaxation or gravity loading for a post embedded in soil with 90 mm asphalt layer.
load is applied without a dynamic relaxation phase, large dynamic waves contaminate the result. Moreover, if the gravity loading is not applied in the model, the soil material shows significantly lower strength and the contact between the soil, the asphalt, and the post does not perform correctly.
Ignoring gravity leads to a lower peak force which requires lower stresses and strains to reach. This causes the peak force to occur at a lower displacement equal to 45 mm which is less than the displacement at peak force for the experiment equal to 70 mm.
4. Component Models
4.1. Steel
A piecewise linear metal plasticity model is used for the steel post. The yield strength of the steel, modulus of elasticity, and Poisson’s ratio are given as inputs using a representative steel stress-strain curve. The common steel parameters presented in Table 1 are employed in this model. An experimental stress-strain curve was obtained using tension tests on samples from guardrail posts in accordance with ASTM E8/E8M [20] . This curve is utilized in the model to account for strain hardening. Shell element formulation number 16 is selected; this element does not exhibit hourglass modes.
4.2. Soil
4.2.1. Yield Surface
Different material models are available in LS-DYNA for modeling of the soil; these were examined to find the most appropriate one to use for modeling of these components. Lewis [26] provides a discussion of available materials in LS-DYNA that are suitable for soil. From these materials, soil and foam (material number 5), soil and foam with failure (material number 14), Mohr-Coulomb
Table 1. Material constants used in the finite element model.
a. The term “system test calibration” refers to the selection of particular material constants based on one selected system test as described above.
(material number 173), Drucker-Prager (material number 193), and FHWA (material number 147) soil material models were selected to be evaluated in this research. The FHWA material model manual [26] and the validation of the model with experimental results [27] were reviewed. The FHWA soil model captures damage evolution, strain softening, pore water pressure effects, strain rate effects, and moisture content effects. The model has numerous parameters, some of which cannot be determined from experiments. Additionally, this study is not focused on the influence of soil parameters such as pore water pressure and moisture content effect and therefore, the research team selected a simpler material model.
After performing the simulations with the various relevant material models, the soil and foam model and Mohr-Coulomb model both proved to be stable under the desired displacement for the current problem. An extensive investigation was conducted to determine the most appropriate of these two for this application. In general, the soil and foam material model is easier to work with; it only has three constitutive parameters for the yield surface and one for pressure cut off. It is also possible to give a volumetric strain versus stress curve as an input. This model is stable for large displacements and low confining pressures. However, the yield surface is smooth, and the material model does not capture the difference in the soil behavior under extension and compression. Many experiments in the past have proven that soil behaves differently under extension and compression [28] . Therefore, the Mohr-Coulomb model is employed to model the soil behavior. The Mohr-Coulomb failure criterion represents a linear envelope that is obtained from a relation between the shear strength of a material and the applied normal stress. The failure criterion is written as
 (1)
(1)
where 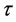 is the shear strength,
is the shear strength, 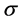 is the normal stress, C is cohesion or the intercept of the failure envelope with the axis, and
is the normal stress, C is cohesion or the intercept of the failure envelope with the axis, and 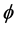 is the angle of the internal friction or the slope of the failure envelope.
is the angle of the internal friction or the slope of the failure envelope.
4.2.2. Soil Classification
To identify the soil type used in the experiment and determine the range of acceptable soil material properties in the literature, the grain size distribution was obtained using sieve analysis. Two processes were used to classify the soil type in this study: Unified Soil Classification System (USCS [29] ) and AASHTO M 147 [30] . The results of the USCS classification are presented in this article; the results from the AASHTO tests can be found in [15] . After determining the soil type based on the grain size distribution, the typical range of mechanical properties of soil can be identified.
The USCS uses symbols for the particle size groups. These symbols and their representations are G for gravel, S for sand, M for silt, and C for clay. These are combined with other symbols expressing gradation characteristics, W for well graded and P for poorly graded. USCS was used to classify the compacted soil that is deposited around the guardrail post in the experimental program. Grain size distribution was obtained using laboratory sieve testing in accordance with AASHTO T 27 [31] . Approximately 47% of the grains passed sieve #4. Therefore, the soil is classified as gravel. Then it is necessary to distinguish if the soil is poorly graded or well graded. From the grain size distribution, the sieve opening size that 10% of the soil sample mass passes through (defined as D10), the sieve opening size that 30% of the soil sample mass passes through (defined as D30), and the sieve opening size that 60% of the soil sample mass passes through (defined as D60) were obtained as 0.093 mm, 0.81 mm, and 9.5 mm, respectively. The coefficient of uniformity and coefficient of curvature were computed using these values as 102.15 and 0.75, respectively [21] . The soil is poorly graded because the coefficient of curvature is less than one. There are 8% fine grains (grains that pass sieve #200) in the soil sample. The fine grains are assumed to be silt (M), so the soil is graded as GP-GM. Moreover, 40% of the soil mass is sand and, therefore, the soil is classified as “poorly graded gravel with silt and sand”.
4.2.3. Calibration of Model
A model without an asphalt mow strip was created to calibrate the soil material properties based on a system level static experiment without an asphalt layer. The soil was modeled using structured hexahedral constant stress solid elements. The mesh was refined until the results did not change noticeably. The final mesh size for soil changes from 25 mm close to the post to 200 mm at locations far from the post. Using a mesh in the soil finer than approximately 25 mm caused instability in the model. Lateral loading in the static test program was simulated as follows. A transverse displacement was applied to the post at 625 mm above the ground level. Mass scaling was not used, and the rate of displacement of the post was varied between 5000 mm/s and 25 mm/s. Analysis of the results demonstrates that rates slower than 50 mm/s give results within 1 percent for all the primary response quantities. Therefore, 50 mm/s was used as the displacement rate of the post to represent quasi-static loading. The kinetic energy of the system was checked and determined to be less than 0.5 percent of the total energy. The contact forces between the post and the soil in the y-direction were calculated to determine the applied force versus displacement curve for the post.
The density of the soil was determined as 2,300 kg/m3 using a laboratory test on a soil sample. This value was used as the soil density in the model. Experimental direct shear tests in accordance with ASTM D3080 [32] were performed on soil samples. Cohesion and peak friction angle were estimated equal to 6.4 kPa and 50 degrees, respectively. These values were initially used in the model, which was subsequently calibrated to capture the peak applied force and the displacement at which the peak force occurs in the load-displacement response of the system. Values of 13 kPa and 45 degrees were found for the cohesion and peak friction angle, respectively, which are in the range of recommended values for gravel with silt and sand used as subbase material ( [7] [21] [33] ). The small value of C was expected for a coarse grain soil since C represents the apparent soil cohesion that is typically associated with strength due to suction in fine grain soils. The peak friction angle in dense soils with coarse grains is usually higher than the critical friction angle. This is due to dilation. To account for dilation and the change of friction angle, a trilinear curve was specified to define the friction angle of the Mohr-Coulomb material model as a function of the effective plastic strain. The friction angle equals 45 degrees for plastic strain values less than 0.4 and linearly decreases to 0.15 between the plastic strains of 0.4 and 0.5. For plastic strains greater than 0.5, the friction angle equals 15 degrees. A standard value of 0.25 was used for the Poisson’s ratio that is typical for the mixture of gravel, coarse sand, and silt [23] . The initial linear elastic portion of the load-displacement curve was used to estimate the shear modulus as 50 MPa, which is in the common range of values for the soil type used in this research [22] . The soil material constants and the procedure used to determine them are summarized in Table 1. A force-displacement comparison between the calibrated finite element model and the experiment without asphalt is given in Figure 7. Based on this figure, the model is capable of predicting force-displacement response for the part before peak force and for the softening part after the peak force.
Figure 7. Comparison between FEA and experiment without an asphalt layer.
4.3. Asphalt
When the asphalt is loaded, part of its deformation comes from viscous behavior. To account for this, the shear modulus of the material was lowered to consider viscous deformation effects under quasi-static loading. The Mohr-Coulomb material model is widely used to model asphalt, and this material model was chosen to model the shear strength of the asphalt. In this study, the density of the asphalt was estimated to be equal 2,300 kg/m3 by laboratory tests. The Poisson’s ratio and friction angle of the asphalt were specified as 0.35 and 35 degrees, respectively, which are typical values for asphalt [24] [25] . The cohesion of the 118-day-old asphalt at the temperature of 20˚C, using experimental unconfined compression tests on asphalt specimens, was estimated to be equal to 0.5 MPa.
The tensile rupture in the asphalt observed in the experimental tests is modeled using element erosion. Element erosion is implemented in this research using the general erosion criteria for solid elements in LS-DYNA. Each criterion is applied independently, and satisfaction of one or more criteria causes deletion of an element from the calculation. The erosion criteria that must be satisfied before an element is removed can be specified by the user. The maximum principal stress criterion was initially used in this research to eliminate the elements when the tensile failure criterion is met. However, the rupture in the asphalt was abrupt when this sole criterion was used, and the strength decreased dramatically, similar to what is commonly observed in very brittle materials. To account for the fact that asphalt can accommodate larger strains before failing under tensile stress, a maximum principal strain failure criterion was added to the material model. Therefore, an element is removed when both the maximum principal stress criterion and the principal strain criteria are satisfied as follows:
・ 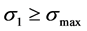 , where
, where  is the failure principal stress and
is the failure principal stress and 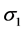 is the current maximum principal stress.
is the current maximum principal stress.
・ 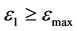 , where
, where 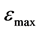 is the failure principal strain and
is the failure principal strain and 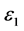 is the current maximum principal strain.
is the current maximum principal strain.
The maximum principal stress at failure can be obtained using Mohr-Coulomb yield criterion as 0.95C/
5. Comparisons between Experiments and Test Simulations
Five experiments with an asphalt layer were conducted and compared to finite element simulations. System behavior after loading from one static experiment (90-mm asphalt layer), FEA with asphalt modeled as discussed above, and FEA with asphalt modeled as rigid are shown in Figure 8. The corresponding force- displacement plots are provided in Figure 9. These results indicate that the material model chosen for the asphalt has a significant effect on the prediction of the system performance and the utilization of a rigid model significantly overestimates the ground level restraint. Numerical results from the remaining experiments
Table 2. Peak force summary for pre-cutting designs.
Figure 8. Condition after static loading on a post with a 90-mm asphalt layer. (a) Experiment; (b) FEA with Mohr-Coulomb asphalt model; (c) FEA with a rigid asphalt model.
Figure 9. Force-displacement comparison between experimental results, FEA with Mohr- Coulomb asphalt model and FEA with rigid asphalt model for a post embedded in a 90-mm asphalt layer.
and finite element simulations with the calibrated Mohr-Coulomb asphalt model are summarized in Table 3. The model is capable of predicting the peak force and maximum ground displacement within 15 percent, with most predictions within 10% compared to experimental results.
6. Effect of Asphalt Material and Geometric Properties
The above model was used to evaluate the relative performance of guardrail posts with various designs including pre-cutting of the asphalt layer. The following sections discuss the effects of the asphalt material and geometric properties on overall performance. The effects of asphalt material constants on the system response are studied because these constants change by aging of the asphalt layer and temperature change. Therefore, it is important to investigate the relationship between the system and these constants.
6.1. Asphalt Rear Distance
The numerical simulations indicate that rear distance of the mow strip behind
Table 3. Comparison of experimental and FEA results.
aNot available due to gage malfunction.
the post significantly affects the post/mow strip system performance. The rear distance was varied using discrete values equal to 0, 150, 300, 600, 1200, 2500 mm and infinity (i.e. infinite medium) with all other system parameters held constant (G = 50 MPa, ν = 0.35, C = 0.5 MPa, f' = 35˚, asphalt thickness = 50 mm, εmax = 0.09, σmax = 0.7 MPa). The peak force applied to the post from the asphalt layer was measured, and the results are presented in Figure 10(a). The results show a proportional relationship between peak force rear distances up to a certain point. There appears to be a cap on this proportionality: after the rear distance reaches approximately 1200 mm, a further increase does not significantly change the response. This occurs because the zone of influence behind the guardrail post is close to 1200 mm. As the rear distance passes 1200 mm, the asphalt behind the guardrail post gets close to its bearing capacity. The bearing capacity of the asphalt layer is not a function of the rear distance.
6.2. Asphalt Thickness
The asphalt thickness was varied using discrete values equal to 0, 25, 50, 90, 125, 175, and 250 mm. The remaining parameters were held constant as in Section 6.1 with the asphalt rear distance equal to 300 mm. The peak force from the asphalt layer applied to the post was measured, and the results are presented in Figure 10(b). The peak force appears to be proportional to the asphalt thickness throughout the range of values investigated. An expanded discussion of the effects of asphalt thickness and rear distance on the system behavior has been presented previously ( [14] [15] ).
6.3. Asphalt Cohesion Value
The asphalt’s cohesion value was varied using discrete values equal to 0.01, 0.1, 0.25, 0.5, 1, and 2 MPa. The principal stress was varied as a function of cohesion using the relationship
Figure 10. Change in system performance with varying rear distance (a), asphalt thickness (b), cohesion (c), friction angle (d), shear modulus (e) and Poisson’s ratio (f).
6.4. Asphalt Friction Angle
The asphalt friction angle was varied using discrete values equal to 1, 5, 10, 15, 20, 30, 40, and 50 degrees. The peak force applied to the post was measured, and the results are presented in Figure 10(d). As can be seen, the peak force is linearly related to the asphalt friction angle when the angle is greater than 20 degrees. For values less than 20 degrees, the asphalt’s strength in tension increases substantially and shear failure occurs instead of principal stress failure. This results in higher peak forces.
6.5. Asphalt Shear Modulus
The asphalt’s shear modulus was varied using discrete values equal to 50, 100, 1,000, and 10,000 MPa. The peak force from the asphalt layer applied to the post was measured, and the results are presented in Figure 10(e). The peak force increases nonlinearly as the shear modulus increases. For values of the shear modulus less than 1000 MPa, the effect of the shear modulus is substantially higher. This can be explained by the nonlinearity in the system. For very low values of shear modulus, large displacements are required to reach the asphalt strength, which causes highly nonlinear secondary effects. However, after the shear modulus passes a threshold value, the nonlinear effects become negligible and increasing the shear modulus after that value does not have a noticeable effect on the system.
6.6. Asphalt Poisson’s Ratio
The asphalt’s Poisson’s ratio was varied using discrete values equal to 0.1, 0.2, 0.3, and 0.4. The peak force applied to the post was measured, and the results are presented in Figure 10(f). From the plot, the peak force changes from 15 kN to 16 kN when the Poisson’s ratio changes from 0.1 to 0.4 which is 7 percent higher. Therefore, change of the Poisson’s ratio does not have a significant effect on the system response. This occurs because the top side of the asphalt layer is free and the asphalt can deform without any resistance in that direction. The free side of the asphalt layer decreases the Poisson’s ratio effect on the stresses in the loading direction. The asphalt strength parameters including friction angle and cohesion which affect the Mohr-Coulomb yield surface has more direct effect on the peak force than Poisson’s ratio.
6.7. Asphalt Pre-Cutting
As discussed in Section 5, if the asphalt is modeled as a rigid material, the asphalt rupture cannot be captured, and the system performance changes significantly. Based on the experimental results, rupture is the primary mechanism of the asphalt failure around the guardrail post. As the rupture propagates, the strength of the asphalt layer decreases up to the point that one portion of the asphalt detaches from the rest of the mow strip. After this occurs, the asphalt has a negligible impact on the system and the soil is the only source of ground restraint. Therefore, one potentially effective way to decrease mow strip restraint would be to introduce predetermined fracture planes (referred to here as “pre-cuts”) in the asphalt layer. A controlled rupture along a predetermined fracture plane in the asphalt avoids uncontrolled crack propagation in a large area and potentially reduces expected maintenance costs. The cuts would be designed based on the experimental and numerical investigation of rupture patterns of the asphalt layer. Two cut patterns were tested experimentally (Figure 11) to verify the FEA with pre-cuts. Additional design patterns were investigated using finite element simulations to find the most effective pattern. Different possible pre-cutting alternatives that were considered are numbered and presented
Figure 11. Pre-cut mow strip design number 4; before test (a); after test (b) and pre-cut mow strip design number 6; before test (c); after test (d).
along with FEA results in Figure 12. Based on the FEA results and analysis of peak forces and stresses in the post, designs number 2 and 3 are determined to be ineffective since they do not significantly decrease the asphalt ground restraint. In design number 3, the cut is applied in the asphalt layer where the asphalt is in tension. Because asphalt is weak in tension, applying a cut in that area does not decrease the asphalt layer’s strength significantly. Design number 2 has the same cut as design number 3 plus a horizontal cut behind the post. The horizontal cut closes on itself when a force is applied to the post and, therefore, it does not cause a decrease in the strength of the layer. From the finite element results, summarized in designs 1, 4, 5, and 6 are effective designs, since they decrease the peak load and ground restraint significantly. These designs shorten the distance that the asphalt rupture needs to propagate until one part detaches from the rest of the layer.
7. Conclusions
Given improvements in computational methods and speed that have occurred since the development of early models for guardrail systems, it is now feasible to perform detailed finite element simulations to characterize the responses at a fundamental material level. Prior FEA methods of the performance of guardrail
Figure 12. Pre-cutting designs for the asphalt mow strip with finite element model simulations.
posts in which the asphalt layer was assumed as a rigid layer are capable of representing the response of cases where the asphalt layer provides excessive levels of restraint; however, such models are not capable of accounting for the influence of the deformability and finite strength of many typical mow strip geometries. As shown in this study, the asphalt finite stiffness and strength of the asphalt layer should be modeled to capture the general non-rigid response of this layer.
The use of a Mohr-Coulomb material model for the soil and asphalt provides an effective representation of the load-deflection response of the guardrail post, soil and asphalt layer system over a broad range of material and geometric parameters. However, erosion based on a combined principal strain and principal stress criterion to capture the rupture of the asphalt layer and the modeling of the contact conditions between the post and the soil are also key attributes of the FE simulation model. To ensure proper performance of the Mohr-Coulomb material model and the contact definition, gravity loading must be applied. Dynamic relaxation should be employed in applying the gravity load to avoid waves caused by the sudden application of the gravity loading to the model.
The finite element models developed in this project were employed to perform parametric studies on pertinent geometric and material variables. The analyses performed indicate that there are definitive combinations of mow strip thickness and rear distance that are more likely to result in higher ground level restraint for guardrail posts. The analyses also indicate that fabricating targeted full-depth cuts in the mow strip significantly reduces the amount of restraint the mow strip provides to a guardrail post.
The effects of asphalt material properties on the system response were studied. The results show that changes in certain material properties significantly affect system response. These properties change by aging of the asphalt layer and temperature change. Therefore, the influence of an asphalt mow strip on the behavior of a guardrail system will change over time in different environmental exposure conditions.
Acknowledgements
The research was sponsored by the Georgia Department of Transportation (GDOT) through Research Project Number 13-21. Any findings, opinions, recommendations or conclusions expressed herein are those of the authors and do not necessarily reflect the views of GDOT.
Cite this paper
Bakhtiary, E., Lee, S.-H., Scott, D.W., Stewart, L.K. and White, D.W. (2017) Evaluation of Guardrail Posts Installed in Asphalt Mow Strips by Static Finite Element Simulation. Open Journal of Civil Engineering, 7, 141-164. https://doi.org/10.4236/ojce.2017.71009
References
- 1. Reid, J. (2004) LS-DYNA Simulation Influence on Roadside Hardware. Transportation Research Record: Journal of Transportation Research Board, 1890, 34-41.
https://doi.org/10.3141/1890-04 - 2. Atahan, A.O. (2010) Vehicle Crash Test Simulation of Roadside Hardware Using LS-DYNA: A Literature Review. International Journal of Heavy Vehicle Systems, 17, 52-75.
https://doi.org/10.1504/IJHVS.2010.029623 - 3. Mohan, P., Dhafer, M., Meczkowski, L. and Bedewi, N. (2005) Finite Element Modeling and Validation of a 3-Strand Cable Guardrail System. International Journal of Crashworthiness, 10, 267-273.
https://doi.org/10.1533/ijcr.2005.0345 - 4. Sicking, D., Reid, J. and Rohde, J. (2002) Development of the Midwest Guardrail System. Transportation Research Record: Journal of the Transportation Research Board, 1797, 44-52.
https://doi.org/10.3141/1797-06 - 5. Plaxico, C., Ray, M. and Hiranmayee, K. (2000) Impact Performance of the G4(1W) and G4(2W) Guardrail Systems: Comparison under NCHRP Report 350 Test 3-11 Conditions. Transportation Research Record: Journal of the Transportation Research Board, 1720, 7-18.
https://doi.org/10.3141/1720-02 - 6. Bligh, R.P., Abu-Odeh, A.Y. and Menges, W.L. (2011) MASH Test 3-10 on 31-Inch W-Beam Guardrail with Standard Offset Blocks. Report FHWA/TX-11/9-1002-4, College Station.
- 7. Dewey, J.F., Jeyapalan, J.K., Hirsch, T.J. and Ross, H.E. (1983) A Study of the Soil-Structure Interaction Behavior of Highway Guardrail Posts. Research Report 3431, College Station.
- 8. Ferdous, M.R., Abu-Odeh, A., Bligh, R.P., Jones, H.L. and Sheikh, N.M. (2011) Performance Limit Analysis for Common Roadside and Median Barriers Using LS-DYNA. International Journal of Crashworthiness, 16, 691-706.
https://doi.org/10.1080/13588265.2011.623023 - 9. Plaxico, C.A., Patzner, G.S. and Ray, M.H. (2007) Finite Element Modeling of Guardrail Timber Posts and the Post-Soil Interaction. Transportation Research Record: Journal of Transportation Research Board, 1647, 139-146.
https://doi.org/10.3141/1647-17 - 10. Wu, W. and Thomson, R. (2007) A Study of the Interaction between a Guardrail Post and Soil during Quasi-Static and Dynamic Loading. International Journal of Impact Engineering, 34, 883-898.
https://doi.org/10.1016/j.ijimpeng.2006.04.004 - 11. Bligh, R.P., Seckinger, N.R., Abu-Odeh, A.Y., Roschke, P.N., Menges, W.L. and Haug, R.R. (2004) Dynamic Response of Guardrail Systems Encased in Pavement Mow Strips. College Station.
- 12. AASHTO (2011) Roadside Design Guide. 4th Edition, AASHTO, Washington DC.
- 13. Dusty, A.R., Bligh, R.P. and Menges, W.L. (2009) Alternative Design of Guardrail Posts in Asphalt or Concrete Mowing Pads. College Station.
- 14. Scott, D.W., Lee, S.H., Bakhtiary, E., Arson, C.F. and White, D.W. (2015) Static Response of Steel Guardrail Posts Driven through Asphalt Vegetation Barriers. Transportation Research Board, Washington DC.
- 15. Scott, D.W., White, D.W., Stewart, L.K., Arson, C.F., Bakhtiary, E. and Lee, S.H. (2015) Evaluating the Performance of Guardrail Posts Installed by Driving through Asphalt Layers. Final Report for Georgia Department of Transportation Research Project 13-21, Atlanta.
- 16. Sicking, D.L., Mak, K.K., Rohde, J.R. and Reid, J.D. (2009) Manual for Assessing Safety Hardware. AASHTO, Washington DC.
- 17. LSTC (2015) LS-DYNA Keyword User’s Manual Volume 1-V971 Build R8.0.0. Livermore Software Technology Corporation.
- 18. Tabiei, A. and Wu, J. (2000) Roadmap for Crashworthiness Finite Element Simulation of Roadside Safety Structures. Finite Element in Analysis and Design, 34, 145-157.
https://doi.org/10.1016/S0168-874X(99)00035-9 - 19. Kulhawy, F.H., Trautmann, C.H., Beech, J.F. and O’Rourke, T.D. (1983) Transmission Line Structure Foundations for Uplift-Compression Loading. Report EPRI EL-6800.
- 20. ASTM (2001) Standard Test Methods for Tension Testing of Metallic Materials. ASTM E8/E8M, West Conshohocken.
- 21. Budhu, M. (2010) Soil Mechanics and Foundations. 3rd Edition, John Wiley & Sons Inc., Hoboken.
- 22. USACE (1982) Bearing Capacity of Soils: Engineering Manual. United States Army Corps of Engineers, Washington DC.
- 23. Bowles, J.E. (2001) Foundation Analysis and Design. 5th Edition, McGraw-Hill, New York.
- 24. Christensen, R.F. and Bonaquist, D.W. (2004) Evaluation of Indirect Tensile Test (IDT) Procedures for Low-Temperature Performance of Hot Mix Asphalt. No. 530, Transportation Research Board, Washington DC.
- 25. Pellinen, T.K., Song, J. and Xiao, S. (2004) Characterization of Hot Mix Asphalt with Varying Air Voids Content Using Triaxial Shear Strength Test. 8th Conference on Asphalt Pavements for Southern Africa, Sun City, 12-16 September 2004.
- 26. Lewis, B.A. (2004) Manual for LS-DYNA Soil Material Model 147. No. FHWA-HRT-04-095, FHWA, Washington DC.
- 27. Reid, Y.D., Coon, J.D., Lewis, B.A., Sutherland, B.A. and Murray, S.H. (2004) Evaluation of LS-DYNA Soil Material Model 147. No. FHWA-HRT-04-094, FHWA, Washington DC.
- 28. Davis, R.O. and Selvadurai, A.P. (2005) Plasticity and Geomechanics. Cambridge University Press, Cambridge.
- 29. USCS (1985) Classification of Soils for Engineering Purposes: Annual Book of ASTM Standards. American Society for Testing and Materials, West Conshohocken.
- 30. AASHTO (2012) Specification for Materials for Aggregate and Soil-Aggregate Subbase, Base, and Surface Courses. AASHTO M147, AASHTO.
- 31. AASHTO (2007) Sieve Analysis of Fine and Coarse Aggregates. AASHTO T27, AASHTO.
- 32. ASTM (2000) Standard Method of Test for Direct Shear Test of Soils under Consolidated Drained Conditions. ASTM D3080, ASTM, West Conshohocken.
- 33. Lekarp, D.A. and Richardson, I.R. (1996) Influences on Permanent Deformation Behavior of Unbound Granular Materials. Transportation Research Record, 1547, 68-75.
https://doi.org/10.3141/1547-10