Journal of Power and Energy Engineering
Vol.07 No.01(2019), Article ID:90289,18 pages
10.4236/jpee.2019.71009
Analysis on Sensitivity of Power System Stability to Generator Parameters
Xiaoming Sun
Department of Electrical Engineering, Chongqing Water Resources and Electric Engineering College, Chongqing, China
Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 30, 2018; Accepted: January 27, 2019; Published: January 30, 2019
ABSTRACT
The sensitivity of power system stability (including transient and dynamic stabilities) to generator parameters (including parameters of generator model, excitation system and power system stabilizer) is analyzed in depth by simulations. From the tables and plots of the resultant simulated data, a number of useful rules are revealed. These rules can be directly applied to the engineering checking of generator parameters. Because the complex theoretical analyses are circumvented, the checking procedure is greatly simplified, remarkably promoting the working efficiency of electrical engineers on site.
Keywords:
Sensitivity Analysis, Power System Stability, Transient Stability, Dynamic Stability, Generator Parameters, Excitation System, Power System Stabilizer

1. Introduction
Generators are the most important component of power system, and thus the level of power system stability is closely related to generator parameters [1] [2] , which include both the parameters of generator models and the parameters of excitation systems and power system stabilizers (PSS). For this, testing and checking the correctness of generator parameters and the appropriateness of generator parameters’ combinations are very important tasks of electrical engineers prior to further analysis of power system stability. In case generator parameters are mistaken or their combinations are inappropriate, it is very likely to cause decision-making errors or deviations from optimal operating points, bringing unforeseen or unfavorable outcomes. Currently, however, strictly and accurately testing and checking generator parameters are actually impractical and impossible; because in modern bulk power system the number of generators is huge, the field tests [3] [4] on each generator are unavoidably time and cost consuming; what’s more, generator parameters may change with time and operating conditions. Therefore, the electrical engineers at the electric power dispatching center really need a simple and practical method for testing and checking generator parameters quickly and efficiently.
The main contribution of this paper is based on the actual engineering experiences of the author. From plenty of simulation experiments, the sensitivity of power system stability (including transient stability and dynamic stability) to generator parameters is analyzed and illustrated in detail, and as a result some feasible and fast rules for testing and checking generator parameters are revealed and summarized, which can be directly adopted by the electrical engineers on site. And because the complex theoretical analyses are circumvented, the testing and checking procedure is greatly simplified so that the working efficiency of electrical engineers is greatly promoted.
2. Generator Models and Parameters
The number and definitions of generator parameters are correlated with specific generator models. To ensure generality, the integral model of generator should be adopted, in which the stator consists of three-phase windings and the rotator consists of salient poles, excitation winding f, d-axis equivalent damping winding D and two q-axis equivalent damping windings g and Q. Based on the Park transform, the per-unit equations of the integral model of generator under dq0 coordinates are as follows (because the magnetic field produced by 0-axis current i0 in stator windings is 0 and has no effect on the electric characteristics of rotator [5] , the equations related to 0-axis component are omitted):
(1)
where , and are the voltages of d-axis, q-axis and excitation wingding f; id, iq, if, iD, ig and iQ are the currents of d-axis, q-axis, excitation wingding f, equivalent damping windings D, g and Q; Ra, Rf, RD, Rg and RQ are the resistances of one-phase stator winding, excitation winding f, equivalent damping windings D, g and Q; yd, yq, yf, yD, yg and yQ are the total magnetic flux linkages of d-axis and q-axis windings, excitation winding f, equivalent damping windings D, g and Q; Xd, Xq, Xad, Xaq, Xf, XD, Xg and XQ are the synchronous reactances of d-axis and q-axis, the armature reaction reactances of d-axis and q-axis windings, the reactance of excitation winding f, the reactances of equivalent damping windings D, g and Q. And, in Equation (1) two assumptions are made: i) assume dyd/dt ≈ 0 and dyq/dt ≈ 0, that is, the electromagnetic transient process is not considered, or the aperiodic component of the stator current is considered in another way [5] ; ii) assume the per-unit value of the electric angular velocity w ≈ 1, making the equations related to d and q linearized.
Apparently, the total magnetic flux linkages yd, yq, yf, yD, yg and yQ in Equation (1) are inconvenient or even impossible to measure in practice, and therefore some measurable variables are introduced to represent these magnetic flux linkages indirectly:
(2)
where , and , are the transient and subtransient electromotive forces of d-axis and q-axis; Xsf, XsD, Xsg and XsQ are the leakage reactances of excitation winding f, equivalent damping windings D, g and Q.
Further, some measurable parameters are also introduced, not only simplifying the equations but also making the equations’ physical meanings clearer:
(3)
where , and , are the open circuit transient and subtransient time constants of d-axis and q-axis.
By substituting Equations (2) and (3) into Equation (1), the 6th-order practical model of generator can be derived:
(4)
where Xsa, , and , are the leakage reactance of stator winding, the transient and subtransient reactances of d-axis and q-axis. And the 6 equations are the voltage equations of stator, excitation winding f, equivalent damping windings D, g and Q, and the motion equation of stator, successively. From Equation (4), the specific position of each generator parameter in the formula is determined clearly.
3. Fast Rules for Testing and Checking Generator Parameters in Models of Different Orders
By reducing Equation (4) to different extent, i.e., neglecting a certain number of windings or introducing new assumptions, the 5th-order, 4th-order, 3rd-order and 2nd-order models of generator can be obtained [6] , and they are not listed out in this paper for brevity. In these models, only one or two parameters have slight discrepancies, and other parameters are the same. It is because of these slight discrepancies that some evident incorrectness of generator parameters can be tested and checked rapidly in terms of the following 6 rules.
1) Rules for the 6th-order model (in this model d-axis, q-axis windings, excitation winding f and equivalent damping windings D, g and Q are all considered, and it is the detailed model of solid steam turbine or non-salient pole machine): , .
2) Rules for the 5th-order model (in this model equivalent damping winding g is neglected, and it is the detailed model of hydraulic turbine or salient pole machine): , .
3) Rules for the 4th-order model (in this model only d-axis, q-axis windings, excitation winding f and equivalent damping winding g are considered, and it is suitable for describing the solid steam turbine): , .
4) Rules for the 3rd-order model (in this model only d-axis, q-axis windings and excitation winding f are considered, and it is suitable for describing the salient pole machine when high computational accuracy is not required): , .
5) Rules for the 2nd-order model (in this model it is assumed that the excitation system is so strong that it can maintain the constancy of and ): = a very big value.
6) Rules for both the salient and non-salient pole machines: .
The rules above are merely the qualitative rules, and a number of quantitative testing and checking rules (variation ranges) [5] [6] derived from engineering experiences are listed in Table 1. From Table 1, two complementary rules can be summarized: a) ; b) .
Provided that the generator parameters are prominently deviating from the aforementioned 6 requirements, the above 2 rules and the reference ranges of Table 1, it is justified in doubting that the parameters are incorrect, and more careful testing means should be taken. However, it is a simple and fast method to test the generator parameters and is very suitable for the preliminary test of the newly obtained parameters.
4. Sensitivity of Power System Stability to Generator Parameters
The testing and checking rules of generator parameters presented in Section 3 are necessary conditions but not sufficient conditions to guarantee power system
Table 1. Quantitative testing and checking rules (variation ranges) of generator parameters.
stability. Whether power system can maintain stable or not depends also on generator parameters’ combinations. This section is aimed at analyzing and illustrating the sensitivity of power system stability (including transient stability and dynamic stability) to generator parameters’ combinations by plenty of simulation experiments. To make it possible for readers to reproduce the simulation results, the IEEE 9-node test system is selected as the simulation model. And the simulation experiments are carried out on one of the most famous simulation software platforms of power system, the Chinese edition BPA, i.e. PSD-BPA (Power System Department―Bonneville Power Administration) [7] [8] [9] .
4.1. Overview of IEEE 9-Node Test System
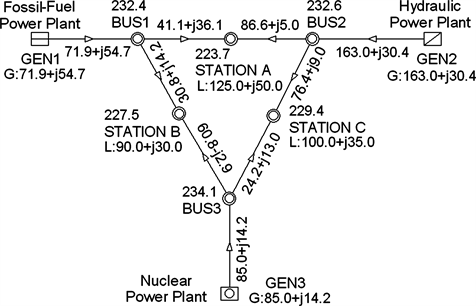
The geographically interconnected diagram of the IEEE 9-node test system is shown in Figure 1, which displays the power flow distribution under normal operation condition. For brevity, this subsection lists out only generator parameters in Table 2, and other detailed parameters, i.e. the steady-state and transient parameters of loads, buses, transmission lines and transformers can be found in [10] . The units of the parameters in Table 2 are the same as those in Table 1, and because Ra ≈ 0, Ra is omitted from Table 2.
By comparing the generator parameters in Table 1 and Table 2, it can be inferred that GEN2 is a hydraulic turbine and GEN3 is a steam turbine. However, GEN1 and GEN2’s and (indicated by the shadings in Table 2) do not strictly comply with the variation range in Table 1, meaning that Table 1 should only be used to judge the prominent incorrectness of generator parameters but
Figure 1. The geographically interconnected diagram of the IEEE 9-node test system. The units of node voltages, active power and reactive power are kV, MW and MVar, respectively; “G” denotes the output energy of generator and “L” denotes the load of station.
Table 2. Generator parameters in IEEE 9-node test system.
not be obeyed inflexibly, and generator parameters’ combinations should also be taken into consideration.
4.2. Sensitivity of Transient Stability of Power System to Generator Parameters
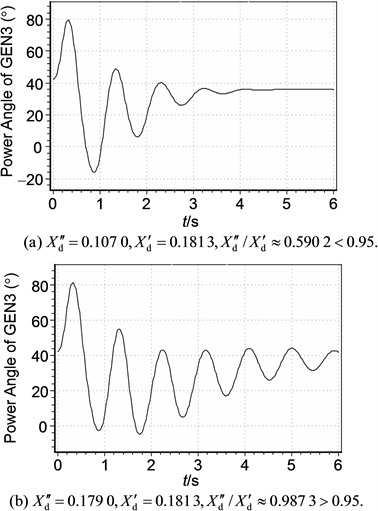
From a good many simulation experiments, the author finds that the transient stability of power system is very sensitive to the values of and . If one of these two values is greater than 0.95, under large-disturbance the power angle curve of generator tends to oscillate greatly and damp slowly, or even diverges, implying generator is out of transient stability. Simulation results in Figure 2 and Figure 3 have illustrated this fact, and therefore the appropriateness of the combinations of , , and can be tested and checked by transient stability simulation experiments.
Figure 2 shows the power angle curves of GEN3 under two different conditions, i.e. and , respectively. The large-disturbance set in the simulation is a three-phase permanent fault on the 220 kV transmission line
Figure 2. The sensitivity of transient stability of power system to .
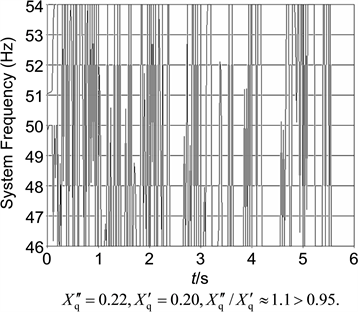
Figure 3. The sensitivity of transient stability of power system to .
BUS1-STATION B: at 0 s, a three-phase short-circuit fault occurs on the side of STATION B; at 0.2 s, the breakers on both sides trip to clear the fault but do not reclose. From the comparison of the power angle curves in Figure 2(a) and Figure 2(b), it is seen that the former returns to a smooth line quickly, while the latter oscillates ceaselessly and cannot damp to a straight line for a very long time.
The large-disturbance set in the simulation of Figure 3 is the same as that in Figure 2. Because the power angle curve of GEN3 with is similar to Figure 2(a), the simulation of Figure 3 considers only the situation of . Again, because GEN3 in this situation has been out of transient stability, the power angle curve oscillates so great that it has exceeded the drawing ranges of PSD-BPA and thus can not be displayed properly. Therefore, the power angle curve here is replaced by the system frequency curve shown in Figure 3, which is recorded by the simulation process supervisor and presents the status of power system indirectly. In Figure 3, the system frequency curve oscillates severely and has already been impossible to return to a straight line, illustrating also that GEN3 is out of transient stability.
4.3. Sensitivity of Dynamic Stability of Power System to Generator Parameters
The common steps to analyze the dynamic stability of power system are as follows.
1) Use the small-disturbance analysis method, i.e. the frequency-domain method, to decompose the oscillation modes, and then calculate the real part, imaginary part, frequency and damping ratio of each oscillation mode, together with the electromechanical circuit correlation ratio, the modulus and phase angle of the right eigenvector, and the participation factors of the generators participating in the oscillation.
2) Use Prony method, a famous time-domain method, to analyze the active powers of some important interconnection transmission lines under large-disturbance and decompose them into a number of oscillation modes as well.
3) Try to find out the oscillation modes under large-disturbance, which are consistent with those found by small-disturbance analysis. If such oscillation modes are found, it can be concluded that the analytic results in frequency domain and time domain are consistent with each other, and that the dynamic stability analysis above is valid.
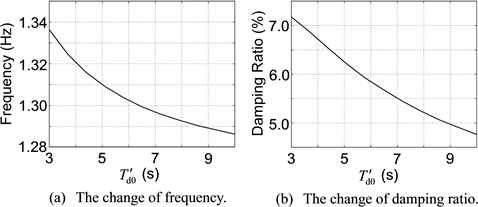
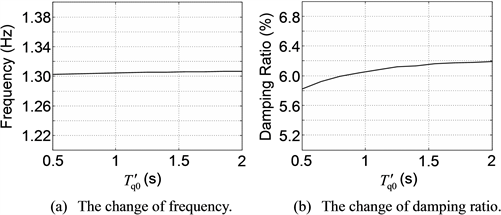
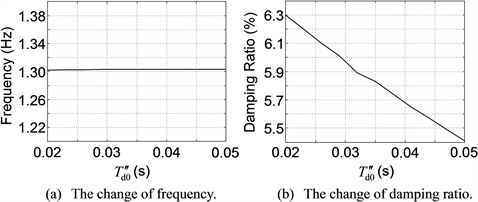
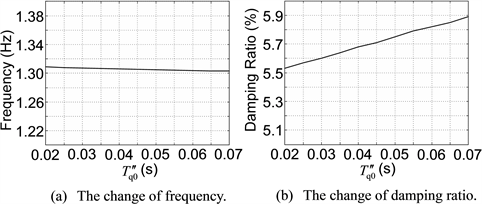
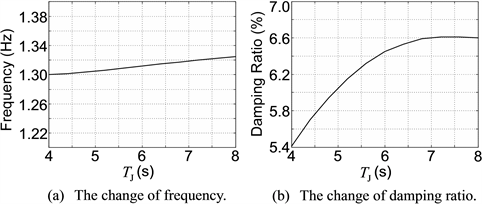
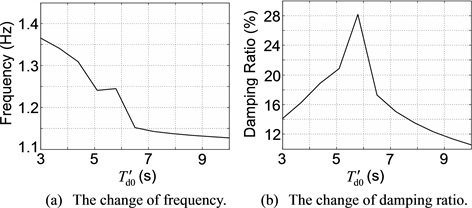
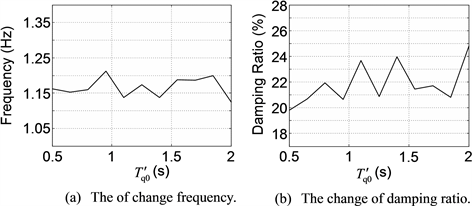
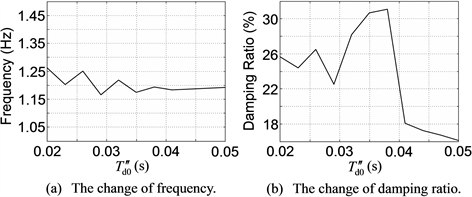
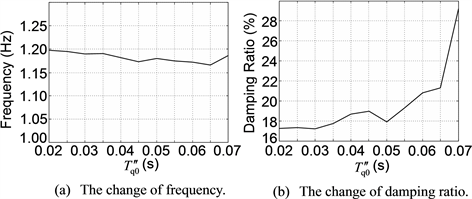
According to the foregoing steps, firstly, apply the small-disturbance analysis to the IEEE 9-node test system. From the small-disturbance analysis, 6 oscillation modes are obtained, wherein only 1 oscillation mode has an electromechanical circuit correlation ratio that is greater than 1.0, meaning that it is the dominant oscillation mode (DOM). Due to this, for brevity, the tables and figures in this subsection show only the details of this DOM. And in Tables 3-7 and Figures 4-8, the sensitivities of the frequency and damping ratio of the DOM to GEN3’s parameters , , , and TJ are illustrated respectively, where the variation ranges of GEN3’s parameters are conform to Table 1.
Table 3 and Figure 4 show that under small disturbance, with increasing, the frequency and damping ratio of the DOM are gradually decreasing. Table 4 and Figure 5 show that under small disturbance, with increasing, the frequency and damping ratio of the DOM are slightly increasing; however, on the whole they are not sensitive to . Table 5 and Figure 6 show that under small disturbance, with increasing, the frequency of the DOM is almost unchanged, while the damping ratio is gradually decreasing. Table 6 and Figure 7 show that under small disturbance, with increasing, the frequency of the DOM is slightly decreasing and not sensitive to on the whole, while the
Table 3. The sensitivity of DOM’s characteristics to under small disturbance.
Figure 4. The curves of the sensitivity of DOM’s characteristics to under small disturbance.
Table 4. The sensitivity of DOM’s characteristics to under small disturbance.
Figure 5. The curves of the sensitivity of DOM’s characteristics to under small disturbance.
Table 5. The sensitivity of DOM’s characteristics to under small disturbance.
Figure 6. The curves of the sensitivity of DOM’s characteristics to under small disturbance.
Table 6. The sensitivity of DOM’s characteristics to under small disturbance.
Figure 7. The curves of the sensitivity of DOM’s characteristics to under small disturbance.
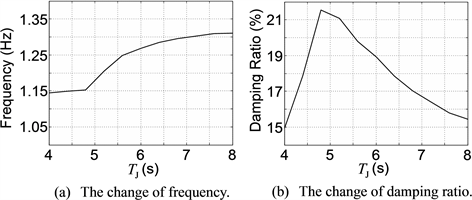
damping ratio has a small tendency of increasing. Table 7 and Figure 8 show that under small disturbance, only when TJ is smaller than a specific value, e.g. 6.5s as shown in Figure 8, are the frequency and damping ratio of the DOM sensitive to TJ.
Table 7. The sensitivity of DOM’s characteristics to TJ under small disturbance.
Figure 8. The curves of the sensitivity of DOM’s characteristics to TJ under small disturbance.
Secondly, apply the large-disturbance analysis to the IEEE 9-node test system to testify the simulation results derived from the preceding small-disturbance analysis. The large disturbance set in the simulation here is the same three-phase permanent fault on 220 kV transmission line BUS1-STATION B as the one in Subsection 4.2. And the resultant active power of the 220 kV transmission line BUS2-STATION A is analyzed by Prony method. Likewise, in Tables 8-12 and Figures 9-13, the sensitivities of the frequency and damping ratio of the DOM to GEN3’s parameters , , , and TJ are illustrated respectively.
Table 8 and Figure 9 show that under large disturbance, with increasing, the frequency of the DOM is gradually decreasing, while the damping ratio is first increasing and then (at about 6 s) decreasing. Table 9 and Figure 10 show that under large disturbance, with increasing, the frequency and damping ratio of the DOM are slightly oscillating across a straight line and their mean values are almost unchanged. Table 10 and Figure 11 show that under large disturbance, with increasing, the frequency of the DOM is not sensitive to and is almost unchanged, while the damping ratio is first increasing and then (at about 0.035 s) decreasing. Table 11 and Figure 12 show that under large disturbance, with increasing, the frequency of the DOM is slightly decreasing, while the damping ratio has a tendency of increasing. Table 12 and Figure 13 show that under large disturbance, only when TJ is smaller than a specific value, e.g. 6.5 s as shown in Figure 13, is the frequency of the DOM sensitive to TJ, while the damping ratio is first increasing and then (at about 4.7 s) decreasing.
Now, by successively comparing the simulation results obtained from the time-domain method under large disturbance with those obtained from the frequency-domain method under small disturbance, we can see that the DOM’s frequency changes with generator parameters in both the time-domain analysis
Table 8. The sensitivity of DOM’s characteristics to under large disturbance.
Figure 9. The curves of the sensitivity of DOM’s characteristics to under large disturbance.
Table 9. The sensitivity of DOM’s characteristics to under large disturbance.
Figure 10. The curves of the sensitivity of DOM’s characteristics to under large disturbance.
Table 10. The sensitivity of DOM’s characteristics to under large disturbance.
Figure 11. The curves of the sensitivity of DOM’s characteristics to under large disturbance.
Table 11. The sensitivity of DOM’s characteristics to under large disturbance.
Figure 12. The curves of the sensitivity of DOM’s characteristics to under large disturbance.
and frequency-domain analysis are consistent with each other, while the DOM’s damping ratio changes with generator parameters, except and , are different from each other. It is because the frequency of an oscillation mode is determined by the inherent structural characteristic of power system, and thus is irrelevant to the operation mode and disturbance type of power system. And it is
Table 12. The sensitivity of DOM’s characteristics to TJ under large disturbance.
Figure 13. The curves of the sensitivity of DOM’s characteristics to TJ under large disturbance.
like the natural vibration frequency of a mechanical system. However, the damping ratio is not determined by the inherent structural characteristic of power system, and therefore it is sensitive to the operation mode and disturbance types of power system.
At the end of this section, two perspectives should be pointed out.
1) The non-dominant oscillation modes’ frequency and damping ratio changes with generator parameters are similar to those of the DOM’s, and therefore the conclusions derived from the DOM are applicable to the non-dominant oscillation modes.
2) If the damping ratio of certain oscillation mode is used to test and check generator parameters, the results obtained under small disturbance and large disturbance should be analyzed separately.
5. Testing and Checking Excitation Systems and PSS Parameters
Except generator parameters per se, the adjustment of the parameters of excitation systems and PSS also plays an important role in ensuring the stability of generators and power system, and therefore the parameters of excitation systems and PSS are always treated as a requisite component of generator parameters. For this, this section proposes the engineering methods for testing and checking the parameters of excitation systems and PSS parameters.
5.1. Testing and Checking Excitation System Parameters
The engineering method for testing and checking excitation systems parameters includes 4 steps.
1) Stop the operation of the PSS of the tested generator.
2) Isolate the tested generator from the electric network.
3) Adjust the reference voltage of excitation system according to a specific function, e.g. step function or ramp function.
4) Investigate whether the output voltage of generator is able to track the reference voltage effectively, and here the “effective track” means that the rising edge is steep, the overshoot is small and the steady area has no great oscillations.
It should be pointed out that a practical and effective way to finish step 4) is to compare the output voltage curve of the tested generator with that of a reference generator which has the correct parameters of both generator and excitation system. Here, the output voltage curve of the reference generator is named as classic curve. If the differences of the two curves are fairly small, it then can be inferred that the excitation system parameters are appropriate from the perspective of application; otherwise, it can be concluded that the excitation system parameters are inappropriate or ineffective, and should be adjusted again or measured directly from field test.
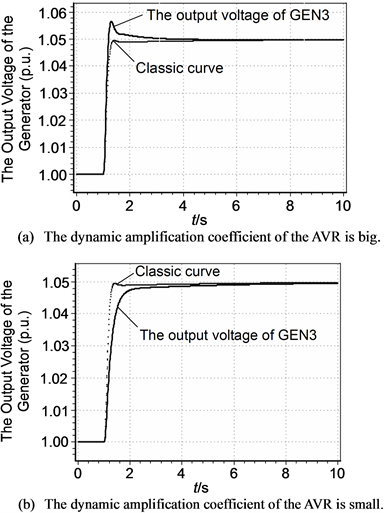
Figure 14 shows the output voltage curve of GEN3 in the IEEE 9-node test system, where for comparison a classic curve is superposed on the figure. From Figure 14(a) and Figure 14(b), it is seen that the differences between the output voltage curve of GEN3 and the classic curve with different excitation system parameters are both acceptably small, meaning that the excitation system parameters
Figure 14. The simulation testing and checking of excitation system parameters.
of GEN3 has good robustness. It should be noted that excitation system parameters depend mainly on the dynamic amplification coefficient of its automatic voltage regulator (AVR) [11] [12] . In Figure 14(a), the dynamic amplification coefficient is relatively big, and it is seen that the response of the output voltage of GEN3 is fast but the overshoot is large; in Figure 14(b), the dynamic amplification coefficient is relatively small, and it is seen that the output voltage of GEN3 has no overshoot but the response is slow. Therefore, on the premise of guaranteeing stability, the dynamic amplification coefficient can be properly adjusted to meet the specific practical requirement.
5.2. Testing and Checking PSS Parameters
The engineering method for testing and checking PSS parameters also includes 4 steps.
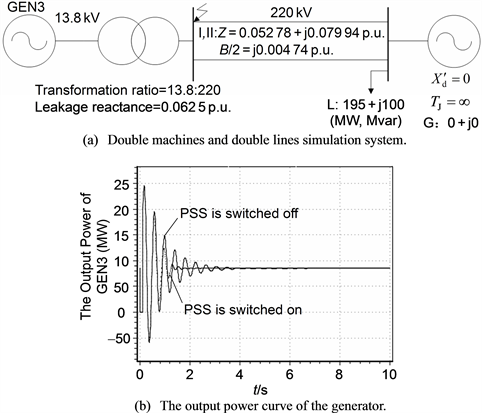
1) Set up the “double machines and double lines” simulation system as shown in Figure 15(a), where GEN3’s parameters are the same as those in the IEEE 9-node test system, and other component’s parameters are labeled in the figure.
2) Set a three-phase permanent fault on transformer’s high-voltage side bus: at 0 s, a three-phase short-circuit fault occurs; at 0.1 s, the breakers on both sides of the transmission lines trip to clear the fault and do not reclose.
3) Switch on and off the PSS of GEN3, respectively.
4) Compare the damping speeds of the oscillations of GEN3’s output power under the two conditions above. If the damping speed of the oscillation of the output power is much faster when PSS is switched on than that when PSS is switched off, it can be concluded that PSS parameters are appropriate; otherwise, PSS parameters should be readjusted.
Figure 15. The simulation testing and checking of PSS parameters.
6. Conclusion
This paper analyzes the sensitivity of power system stability to generator parameters, including the parameters of generator, excitation system and PSS from plenty of simulation experiments. Because the simulation processes are closely related to the engineering practice and do not involve any complex theoretical analysis, the summarized rules and conclusions are evident and practical, and thus can be directly referenced or applied by electrical engineers. Based on these rules and conclusions, some feasible methods are proposed for testing and checking generator parameters quickly, which may greatly promote the working efficiencies of electrical engineers. Although the simulation examples used in this paper is very simple, the resultant conclusions are of generality and can be easily testified by readers in their researching and working activities.
Acknowledgements
This research is supported by the Science and Technology Research Project of Chongqing Educational Committee (KJ1603605) and the Natural Science Fund Project of Yongchuan District Science and Technology Committee (Ycstc, 2016nc3001).
Conflicts of Interest
The author declares no conflicts of interest regarding the publication of this paper.
Cite this paper
Sun, X.M. (2019) Analysis on Sensitivity of Power System Stability to Generator Parameters. Journal of Power and Energy Engineering, 7, 165-182. https://doi.org/10.4236/jpee.2019.71009
References
- 1. Kim, D.J., Moon, Y.H., Lee, J.J., Ryu, H.S. and Kim, T.H. (2018) A New Method of Recording Generator Dynamics and Its Application to the Derivation of Synchronous Machine Parameters for Power System Stability Studies. IEEE Transactions on Energy Conversion, 33, 605-616. https://doi.org/10.1109/TEC.2017.2772234
- 2. Hasan, K.N., Preece, R. and Milanović, J. (2018) Application of Game Theoretic Approaches for Identification of Critical Parameters Affecting Power System Small-Disturbance Stability. International Journal of Electrical Power and Energy Systems, 97, 344-352. https://doi.org/10.1016/j.ijepes.2017.11.027
- 3. Izena, A., Kihara, H., Shimojo, T., Hirayama, K. and Furukawa, N. (2008) Generator Voltage Building-Up Field Test for 500 kV Transformer Energization for Black-Start Power System. IEEJ Transactions on Power and Energy, 128, 641-646. https://doi.org/10.1541/ieejpes.128.641
- 4. Hasegawa, K. and Imai, Y. (2002) Field Test of 70 MW Class Superconducting Generator. Cryogenics, 42, 191-197. https://doi.org/10.1016/S0011-2275(02)00034-6
- 5. Leonard, L.G. (2012) Power System Stability and Control. 3rd Edition, JCRC Press Inc., Taylor & Francis Group, Boca Raton.
- 6. IEEE (2007) IEEE Guide for Synchronous Generator Modeling Practices and Applications in Power System Stability Analyses. Revision of IEEE Std., 1110-1991. https://ieeexplore.ieee.org/document/1251520
- 7. Guo, Y.Z., Huang, R.M., Zhu, M. and Cai, X. (2018) Reexamination of New-Generation General Wind Turbine Models in PSD-BPA Transient Stability Simulation Program. Proceedings of the 13th IEEE Conference on Industrial Electronics and Applications, ICIEA 2018, Wuhan, 31 May-2 June 2018, 588-593. https://doi.org/10.1109/ICIEA.2018.8397784
- 8. Yan, C.Y., Wang, M. and Lu, J.J. (2013) The Contrast between the Models’ in PSD-BPA and those in PSASP. Advanced Materials Research, 614-615, 1055-1064. https://doi.org/10.4028/http://www.scientific.net/AMR.614-615.1055
- 9. Han, S., Rong, N., Sun, T. and Peng, X.J. (2013) Study on Conversion between the Common Models of PSD-BPA and PSS/E. Proceedings of 2013 IEEE 11th International Conference on Electronic Measurement and Instruments, ICEMI 2013, Harbin, 16-19 August 2013, 64-69. https://doi.org/10.1109/ICEMI.2013.6743040
- 10. Power System Department of China (2007) PSD Software Program Training Manual. https://wenku.baidu.com/view/0282520a79563c1ec5da713f.html
- 11. Yegireddy, N.K., Panda, S., Papinaidu, T. and Yadav, K.P.K. (2018) Multi-Objective Non-Dominated Sorting Genetic Algorithm-II Optimized PID Controller for Automatic Voltage Regulator Systems. Journal of Intelligent and Fuzzy Systems, 35, 4971-4975. https://doi.org/10.3233/JIFS-169781
- 12. Hoque, M.M. (2014) Design, Implementation and Performance Study of Programmable Automatic Voltage Regulator. Journal of Electrical Systems, 10, 472-483.