Journal of Power and Energy Engineering
Vol.03 No.05(2015), Article ID:56718,6 pages
10.4236/jpee.2015.35009
Dynamic Model Study and Analysis of DME Auto-Thermal Steam Reforming Reaction
Yan Gao, Cong Li
Shanghai University of Engineering Science, Shanghai, China
Email: 449284019@qq.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2015; accepted 24 May 2015; published 27 May 2015
ABSTRACT
Through the study of the kinetics of dimethyl ether steam reforming reaction, a two-dimensional model of the reactor is established. At the same time, rate equations of simplified elementary reactions of DME steam reforming reaction are deduced by the mechanism of Langmuir-Hinshel- wood, and the rate constants are obtained by correcting the pre-exponential factor of Arrhenius equation. Finally, the analog data of DME steam reforming reaction under a variety of conditions are obtained, and making a simulation diagram. The two-dimensional model is substantially correct because of the analog data more in line with a variety of knowledge.
Keywords:
Dimethyl Ether (DME), Kinetic Model, The Reaction Rate, Reforming Reaction

1. Introduction
Dimethyl ether has the advantage of economy, security, and the sources of diversity, bound from the research stage to the industrial stage [1] . However, due to the engine of DME has a shortcoming of fire earlier, making it smaller work load range [2] , while the hydrogen fuel cell and electric vehicles are being tested and toward industrialization in the world, but blocked in hydrogen storage technology [3] , so automotive fuel reforming is an important way to solve the problem of the hydrogen energy [4] [5] .
DME is an ideal vehicle fuel, but also has capability of chemical hydrogen storage. Therefore, many scholars have been studied to the DME reforming processes [6] -[8] , confirming its value of commerce and scientific and finding some technical issues, such as the hydrogen yield. Generally speaking, the main method of DME reforming is the traditional methods and the plasma reforming method. The traditional methods include Auto- thermal reforming, steam reforming, partial oxidation reforming and so on. However, the study of kinetics model about DME reforming reaction is still relatively lacking in the current. Weiqi Qian et al. [9] used the quasi-steady method to establish a simplified chemical kinetic model for combustion of hydrocarbon fuels, effectively reducing the reaction components. Solution variables and differential equations are reduced when it is calculated in the flow field, improving the efficiency of calculation. Yumin Chen et al. [10] conducted kinetic analysis to the process of methane auto-thermal reforming reaction. Wang Feng et al. [11] conducted kinetic analysis to the process of methanol steam reforming in the micro-reactor. Dongmei Feng et al. [12] made the Kinetic Study of the process about dimethyl ether steam reforming reaction using of a catalyst CuO − ZnO − Al2O3 + ZSM − 5. This article will use the catalyst 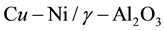 to make kinetic studies of Dimethyl ether steam reforming reaction, establishing a two-dimensional model of the reactor, deducing the rate equation of simplified elementary reaction, learning the influence of the reaction rate and the mole fraction with temperature and time.
to make kinetic studies of Dimethyl ether steam reforming reaction, establishing a two-dimensional model of the reactor, deducing the rate equation of simplified elementary reaction, learning the influence of the reaction rate and the mole fraction with temperature and time.
2. Experimental Methods
During the whole experiment, the space velocity of DME steam reforming reactor is 0.3 m/s. The molar ratio of water and DME is 1 to 3. The feed mole fraction of dimethyl ether is between 5 and 15. The flow rate of DME is 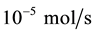 in the feed mouth. The pressure inside the reactor is 0.1 Mpa and the range of temperature is 200˚C to 400˚C.
in the feed mouth. The pressure inside the reactor is 0.1 Mpa and the range of temperature is 200˚C to 400˚C.
3. The Kinetic Models
3.1. Reforming Reactor Model
The kinetic model of DME steam reforming reactor applies to a two-dimensional model. Although the kinetic parameters of the reactor are difficult to be determined in the process of reaction, it can improve the accuracy of the change of amount of substance and energy conversion. The two-dimensional model is non-continuous, axial symmetry, similar to the two-dimensional reactor of Groppi, G. et al. [13] . The reaction of DME and H2O on the catalyst coating layer of the reactor produced H2 and oxides of carbon. In the course of the reaction, the mass of reactants and product are equal, the mass conservation equation as follows:
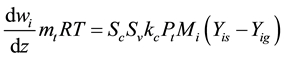 (1)
(1)
Because the reactants are gas and in the high-speed motion in the reactor, and so axial diffusion of the gas mass is negligible. Because the heat exchanger conduit wall can isolate gas, so the radial diffusion of the gas mass in the reactor is also negligible. Then the above equation can be simplified to as follows:
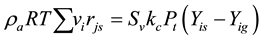 (2)
(2)
Further, on the catalyst coating layer of the reactor, the mass conservation equation of each element in the course of the reaction and diffusion is as follows:
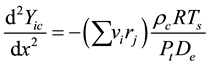 (3)
(3)
In this reactor, if the catalyst coating layer is a uniformly thickness, the boundary conditions are shown in Table 1. The average thickness of the catalyst coating layer is about 35 microns, while the effective diffusion coefficient 
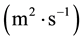 is estimated by random pore model [14] . On the catalyst coating layer, according to the mass conservation of the elements, the average reaction rate
is estimated by random pore model [14] . On the catalyst coating layer, according to the mass conservation of the elements, the average reaction rate  can be obtained:
can be obtained:
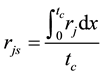 (4)
(4)
Similar to the gas phase mass balance of (2), axial and radial dispersions were neglected in the gas-phase heat balance:
Table 1. Boundary conditions for the 2D monolithic reactor wash-coat mass balance and solid heat balance.
 (5)
(5)
External energy transfers to DME and water using of the heat conduction manner of the axial and radial through the reactor wall and the catalyst coating layer, using the equation:
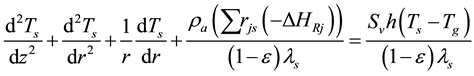 (6)
(6)
Wherein,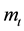 ―The total mass flow rate
―The total mass flow rate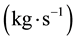 , M―Molar mass
, M―Molar mass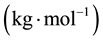 ,
,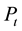 ―The total pressure (Pa),
―The total pressure (Pa),




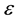



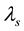






3.2. Kinetics Model of DME Steam Reforming Reaction
There are three major reactions in the process of DME steam reforming [15] , which can be shown in Table 2, and DME oxidation reaction is the heat source. In the ideal case, the inlet of reactor is water, DME and O2, and the outlet is CO2 and H2. When each elementary reaction is in a relatively stable state of the reaction rate, adsorption equilibrium constant of H2 and CO2 on the catalyst is relatively small, and it can be ignored as the case in the calculation process. The reaction rate equation takes Langmuir-Hinshelwood model of water molecules and other molecules competitive adsorption, and it is ideal for surface reaction.
3.3. Parameters of the Kinetic Model
Arrhenius equation is used to solve the rate constants, and the expression is:

Due to the range of experimental temperature is 200˚C to 400˚C, so temperature variation range is small, and the pre-exponential factor A is corrected and the activation energy not, then Arrhenius equation:

where, 
Then, the activation energy 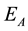


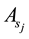

The fitting parameter of Adsorption equilibrium constant 

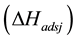
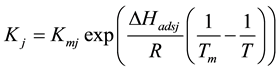
The main elementary reaction rate constant can be obtained by Equation (8) and (9) using ofrate constant 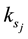
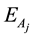
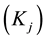


4. Results and Discussion
The legend of all graphics is the same with the legend of Figure 1(a).
Table 2. Kinetic model overall reactions and rate expression.
Table 3. Fitted kinetic parameter values and 95% confidence intervals.

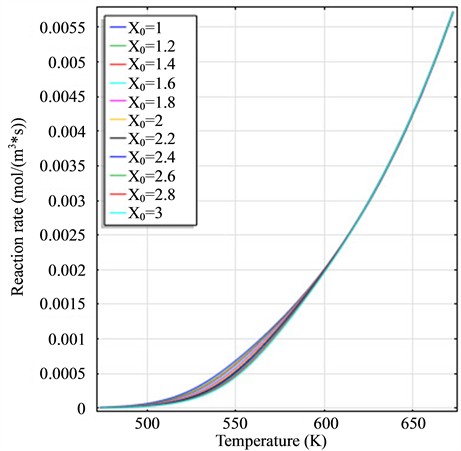
Figure 1. (a) The variation diagram of 



Figure 1 is the graph of rate variation of each reaction, and the equation of temperature changing with time is 473 + 200t. Figure 1(a) is the variation diagram of rate and temperature for the oxidation reaction of DME, with increasing temperature, 


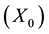
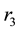








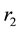



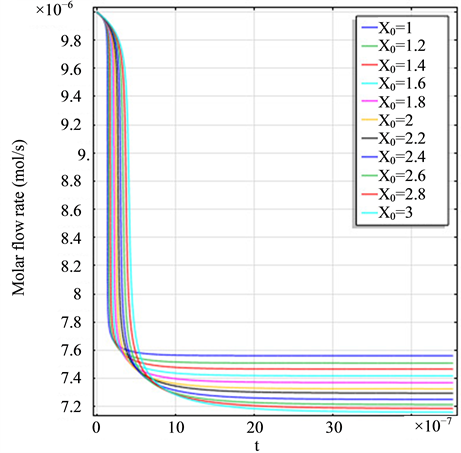
Figure 2(a) is the molar flow rate variation graph of H2 with time, which rapidly increases to stabilize with increasing time, and it increases with increasing 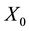




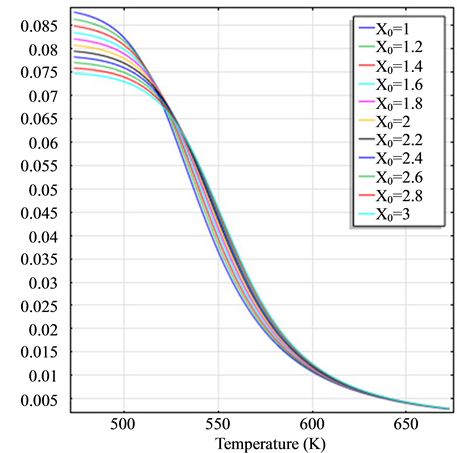
Figure 2. (a) The molar flow rate variation graph of H2 with time; (b) The molar flow rate variation graph of DME with time; (c) The mole fraction graph of H2 with temperature variation; (d) The mole fraction graph of DME with temperature variation.
and H2 to temperature is the maximum, indicating that their speed of response here has a jump, which can be proven from Figure 1(b), Figure 1(c) and Figure 1(d). When the curve of Figure 2(a) and Figure 2(b) trend to steady, the curve of Figure 2(c) and Figure 2(d) are becoming more stable, indicating that the reactants at the inlet of the reactor achieves to conditions optimally. That is, if this state is changed, the reactants conditions of the reactor at the inlet need to change.
5. Conclusion
The two-dimensional model is substantially correct because of the analog data more in line with a variety of knowledge. For example, the ratio of water-DME and the ratio of oxygen-DME are important step of controlling the hydrogen yield. Finally, this article can provide important theoretical references to the kinetics of dimethyl ether steam reforming reaction.
References
- Yu, Y.-F. and Jing, Y.-H. (2010) The Research Analysis of the Application of the Vehicle DME Fuel. Northwest Coal, 6.
- Shudo, T. and Yamada, H. (2007) Hydrogen as an Ignition-Controlling Agent for HCCI Combustion Engine by Suppressing the Low-Temperature Oxidation. International Journal of Hydrogen Energy, 32, 3066-3072. http://dx.doi.org/10.1016/j.ijhydene.2006.12.002
- Sun, D.-L. (2011) Development and Challenge for On-Board Hydrogen Storage. Chinese Journal of Nature, 33, 13-18.
- Zhang, W.G., Lu, W.D. and Yan, Y. (2010) Experiment on the Performance of Steam Reforming by Dimethyl Ether. Transactions of the Chinese Society for Agricultural Machinery, 41, 6-16.
- Ji, C.W., Ju, B.J. and Dai, X.X. (2013) Mixed Combustion Performance Experiment of Syngas Produced by Ethanol Steam Reforming for Engine. Transactions of the Chinese Society for Agricultural Machinery, 44, 27-32.
- Feng, D.M., Wang, J.F. and Wang, D.Z. (2007) Production of Hydrogen from Dimethyl Ether over Catalysts. Sciencepaper Online.
- Li, C., Wang, Y.S. and Fan, P.Q. (2012) Numerical Analysis and Experimental Study of Hydrogen Production from Dimethyl Ether Steam Reforming. Science China Chemistry, 9.
- Zheng, Z.L. and Li, S.L. (2013) Thermodynamics Analysis of Hydrogen Production in Vehicle DME Steam Reforming Reaction System. Transactions of the Chinese Society for Agricultural Machinery, 9.
- Qian, W.-Q., Yang, S.-H., Xiao, B.-G. and Le, J.-L. (2007) Development of Reduced Chemical Reaction Kinetic Model for Hydro-Carbon Fuel Combustion with Quasi-Steady-State Approximation Method. Acta Aerodynamica Sinica, 3.
- Chen, Y.-M., Zhao, Y.-C., et al. (2011) Thermodynamic and Kinetic Analyses for Hydrogen Production via Methane Autothermal Reforming. Journal of Fuel Chemistry and Technology, 8.
- Wang, F., Zhou, J., Wang, G.J. and Zhou, X.J. (2011) Kinetics Study of Methanol Steam Reforming Hydrogen Production in a Microreactor. Acta Aerodynamica Sinica, 4.
- Feng, D.M., Wang, Y.Y., Wang, D.Z. and Wang, J.F. (2009) Steam Reforming of Dimethyl Ether over
: A Kinetic Study. Chemical Engineering Journal, 2.>http://html.scirp.org/file/9-1770129x121.png" class="200" />: A Kinetic Study. Chemical Engineering Journal, 2.
- Groppi, G. and Tronconi, E. (2001) Simulation of Structured Catalytic Reactors with Enhanced Thermal Conductivity for Selective Oxidation Reactions. Catalysis Today, 69, 63-73. http://dx.doi.org/10.1016/S0920-5861(01)00356-X
- Froment, G.F. and Bischoff, K.B. (1990) Chemical Reactor Analysis and Design. 2nd Edition, John Wiley & Sons, New York.
- Daubert, T.E. and Danner, R.P. (1989) Physical and Thermodynamic Properties of Pure Chemicals (Data Compilation). Hemisphere Publishing Corporation, New York.
- Creaser, D. and Creaser, D. (2010) Kinetic Modeling of Autothermal Reforming of Dimethyl Ether. Industrial Engineering Chemistry Research, 49, 9712-9719.






 : A Kinetic Study. Chemical Engineering Journal, 2.>http://html.scirp.org/file/9-1770129x121.png" class="200" />: A Kinetic Study. Chemical Engineering Journal, 2.
: A Kinetic Study. Chemical Engineering Journal, 2.>http://html.scirp.org/file/9-1770129x121.png" class="200" />: A Kinetic Study. Chemical Engineering Journal, 2.