Received 30 March 2015; accepted 16 May 2015; published 19 May 2015

ABSTRACT

Polymers typically have intrinsic thermal conductivity much lower than other materials. Enhance- ment of this property may be obtained by the addition of conductive fillers. In this research, epoxy nanocomposites with exfoliated graphite nanoplatelets are prepared and characterized. The chosen approach requires no surface treatment and no sophisticated equipments allowing one to pro- duce composites on a pilot scale. A significant increase of the thermal conductivity with the increasing of the graphite fillers content is nevertheless observed on 4 mm thick specimens. Our results viewed in the latest scientific findings suggest that the choice of resin is an important parameter to move towards composite materials with high thermal conductivity.

Keywords:

Composite Epoxy-GnP, Thermal Conductivity, Graphite Nanoplatelets, Exfoliated Graphite

1. Introduction

Epoxy resins, through their chemical and electrical resistances, are used for adhesives, protective coating, embedding, casting and composites, in electrotechnical industry [1] . They find applications for medium and high voltage indoor electrical insulators such as switch, because of their good resistance to long term stress and temperatures up to 85˚C.

Polymers typically have intrinsic thermal conductivity much lower than those for metals or ceramic materials. A typical value for epoxy material thermal conductivity is 0.20 ± 0.01 W/mK. The thermal conductivity of polymers has been traditionally enhanced by the addition of thermally conductive fillers, including among others graphite and carbon nanotubes [2] [3] . Many applications would benefit from the use of dielectric polymers with enhanced thermal conductivity. For example, when used as heat sinks in electric or electronic systems, a thermal conductivity from about 1 to 30 W/mK is required [4] . Obtaining composites having both usual polymer processability and thermal conductivities higher than 4 W/mK is however very challenging [5] .

Nanocomposites differ from conventional composite materials due to the exceptionally high surface to volume ratio of the filler phase. The area of the interface between the matrix and filler phase is typically an order of magnitude greater than for conventional composite materials. As a result, a relatively small amount of nanoscale fillers may have an observable effect on the macroscale properties of the composite. Carbon-based fillers are promising fillers, due to their high thermal conductivity lightweight. Moreover, natural graphite is still abundant and its cost is quite low compared to the other nano-size carbon materials. Enhancement of thermal conductivity by 100% for only 1% vol. of multiwall carbon nanotubes (MWCNT) or multilayer graphene loadings was achieved [6] .

Graphene single sheet material exhibits in-plane sp² hybridized C thermal conductivity ~5000 W/mK at room temperature when suspended [7] . However, as soon the material is in contact with a support or even stacked with another graphene sheets, the lateral interactions induce a drastic decrease (60% less) of the conductivity which is in the range of 2000 W/mK.

Graphite nanoplatelets (GnP) in the thickness range of 10 - 100 nm have drawn interest due to their fair thermal conductivity κ ≈ 1500 W/mK at room temperature and a cost of production consistent with industrial scale production [8] . In this work, the chosen approach is to disperse commercial GnP in an industrial epoxy resin without any additional chemicals and non-sophisticated equipment. This paper aims to understand the main parameters which might influence the improvement of thermal conductivity: the chemical nature and viscosity of the resin/hardener system; the structure at micron scale and nanoscale; the form and size dispersion of the fillers; the filler content and the chemical interactions between fillers and the matrix. Our approach considers the analysis and the calculations of physicochemical parameters for make a comparison of the latest scientific findings concerning the role of epoxy resin in nanoplatelet-epoxy composites. We claim that the choice of epoxy resin is an important parameter to move towards composite materials with high thermal conductivity.

2. Experimental

2.1. Materials and Method

Graphite nanoplatelets (GnP) were purchased from XG Sciences, Inc. GnP consisting of small stacks of graphene are fabricated by acid intercalation and microwave heating [9] . The size and thickness of GnP are controllable during fabrication. The M grade (GnP M) are flakes made of elementary thin particles having average thicknesses in the range of 6 - 8 nm and an average equivalent particle diameter of 25 microns as XG Sciences specification. The manufacturer reported oxygen content ≤ 1% wt. and residual acid content ≤ 0.5% wt. The synthetic graphite powder was purchased from Sigma Aldrich.

In this work, a Huntsman epoxy system is carried out at the thermosetting matrix polymer. The epoxy system includes three components: 1) The resin: diglycidyl ether of bisphenol A which is a viscous epoxy monomer (CY225), clear colorless/yellow liquid with a dynamic viscosity of 8.5 - 15 Pa.s, with a density of 1.17 - 1.20 g/cm³ and an epoxy content of 5.10 - 5.30 equivalent/kg at 25˚C; 2) The hardener:Aradur HY925 is an aromatic cyclic anhydride acid (Tetrahydromethyl-1,3-isobenzofurandione), yellow liquid with a viscosity of 0.3 - 0.4 Pa.s with a density of 1.19 - 1.22 g/cm³ at room temperature; 3) A catalyst, included in the resin, being a quaternary ammonium halide salt. The mixing ratio for these components is CY225:HY925 = 100/80 respectively as per the datasheet of the supplier Huntsman, Switzerland. The curing reaction is shown in Figure 1, and occurs by polymerization chain reaction and includes opening of the anhydride rings by the attack of alkoxy group from the monomer to create the species of propagation (anionic ester) catalyzed by quaternary ammonium halide (anionic polymerization), the next step of the reaction follows with an epoxy group which attacks another alkoxy

group to form a diester, spread on to result in the formation of the polymer network [10] .

The carbon fillers, previously heated at 120˚C during 24 hours, were dispersed into the HY925, after that, the CY225 was added using the method of mechanical stirring at 10,000 rpm, the resulting mixture was later degassed at 60˚C and then cured into an oven for 100˚C during 5 hours followed by post curing at 140˚C during 8 h. As reference system, an epoxy resin was prepared without load, and we optimized the conditions to ensure the reproducibility of the polymer matrix. Nanocomposites with different weight percentage of the filler varying from 0.2% vol. to 2.67% vol. were prepared. The densities used for the calculation of the %vol. loading are: synthetic graphite and GnPM, 2.3 g/cm³ and epoxy, 1.187 g/cm³ respectively.

2.2. Microscopy

Morphological characterization of the fillers was done using a field emission scanning electron microscope (FESEM) from FEI Quanta 200 (Carl Zeiss, Germany). The specimens were prepared by both techniques: 1) deposition of the raw powder on a conductive support and 2) deposition of a drop from the dispersion obtained after ultrasonification during 30 minutes on a silicon wafer (Si/SiO₂) with 500 nm of thickness. Most of the images were observed under 1 - 10 kV acceleration voltage.

2.3. Specific Surface Area

The Brunauer-Emett-Teller (BET) surface area was determined by N₂ adsorption measured at 77 K using a BET specific surface area analyzer by Micromeritics ASAP 2010 automatic physisorption analyzer with multi-gas option. During all measurement phases, sample equilibration was determined by monitoring the rate of pressure change in the manifold as a function of time. All samples were outgassed at 110˚C under vacuum 24 h before.

2.4. TGA Measurements

We used thermogravimetric analysis to determine the weight loss of the fillers as a function of the temperature. The measurements were carried out by a TGA/DSC 1 Star System made Mettler Toledo in dynamic mode. The temperature was raised from room temperature to 1000˚C with a ramp rate of 10˚C/min and tests were conducted under continuous flow of 60 mL/min of oxygen (99.9%).

2.5. Thermal Conductivity Measurements

The thermal transport performance of the fabricated composite was characterized by the transient plane source technique based on a disk sensor composed of a double spiral nickel wire for rapid thermal conductivity measurements [11] [12] . In our study, a Hot Disk TPS 2500 unit and a Kapton insulated sensor (radius 3.200 mm) were used to measure the thermal conductivity for the composites at room temperature (22˚C). The sensor is sandwiched between both pieces of the same polished composite slab (thickness > 3.5 mm), for all the samples’ surfaces are well smooth and parallel by means of 400 and 600 grit 3M emery paper in order to downsize the surface irregularities, the contact between the flat and thin TPS sensor and the polished sample are optimal, leading to a substantial reduction in contact thermal resistance between both elements. A small constant current is supplied to the sensor which has the role of heat source and temperature monitor at the same time. The hot disk method considers only data stemming from heat propagation in the materials for its calculations. The determined values therefore represent the bulk properties of the samples. The probing depth i.e. the distance from the sensor edge to the nearest surface of the sample must be thinner than 3 mm. For accuracy issue, the mean deviation parameter was considered correct when it is below 1 × 10⁻³. For each composite, the heating power supplied by the sensor is fixed at 20 mW between 10 and 20 s. The associated changes in temperature were recorded and an average of seven thermal conductivity measurements per sample was collected.

3. Results

Epoxy thermosetting resins are three-dimensional network of bonds (cross-linking). The macromolecules resulting from this architecture are made of oxirane groups, resulting from the reaction between the resin and the hardener which kinetic maybe control by the addition of an accelerator. One of the most commonly used resin in the insulation industry is derived from the reaction between bisphenol A (4,4’-(propane-2,2-diyl) diphenol) better known as BPA (Figure 2(a)) and epichlorohydrin (2-(chloromethyl)oxirane), synthesized from propene via allyl chloride) in the presence of sodium hydroxide. The product of the reaction is, diglycidyl ether of bisphenol A (2-[[4-[2-[4-(Oxirane-2-ylmethoxy) phenyl] propan-2-yl]phenoxy]methyl]oxirane) with the commercial name of DGEBA (Figure 2(b)).

There is another kind of resin family. Among them, resin made of Bisphenol F (2-[(4-hydroxyphenyl) methyl] phenol), often simply called BPF. It results from the reaction between phenol and formaldehyde, and can be epoxidized with the hydroxyl functions of epichlorohydrin (Figure 2(d)).

An important characteristic of epoxy resins is the epoxide content which is used to calculate the amount of co-reactant (hardener) required when curing epoxy resins. This is commonly expressed as the number of epoxide equivalents in 1 kg of resin (Eq./kg), or as the equivalent weight, which is the weight in grams of resin containing 1 mole equivalent of epoxide (g/mol).

3.1. Carbon Fillers Characterization

The morphology of the fillers was studied by SEM images reported on Figure 3, the results shows that both carbon fillers are polydispersed materials with agglomerates in the range 1 - 25 microns. The Figure 3(a) shows

nanoplatelets of irregular shape and a wide thickness distribution. We may observe elementary translucent particles of 1-2 microns lateral size (Figure 3(e)-(d)).

The lateral (degree of reduction after high energy shear mixing) and thickness (degree of graphite exfoliation) of the elementary particles of the filler powder are roughly estimated by statistical analysis on the basis of optical and scanning electron microscopy. These parameters were estimated with the help of the Digimizer 4.0 software, taking in account the parameters for convert the measure of the image in 2D in a measure in 3D, according to the theory developed by Li et al. [13] . We estimate that the GnPM elementary average particle lateral size is about 10 ± 3 microns and 45 ± 14 nm of thickness. From this data, the aspect ratio for GnP M was estimated to be ~200 and the aspect ratio for synthetic graphite: ~8. (The aspect ratio is defined as the ratio of the average width to the average thickness of the nanoplatelets).

The degree of dispersion of the graphite particles may depend on one hand on the extent of the shearing exerted on the fillers and on the other hand on the possible absorption of some monomers and polymers into the pores and galleries of agglomerates and around exfoliated graphites [14] . Intercrystalline porosity may be a parameter for the characterization of physical properties.

Table 1 exhibits the specific surface area measured on the raw materials. It is worth to notice that the specific surface area of 135 ± 15 m²/g given by the supplier is a little bit overestimate.

If we assume that GnP are nanoparticles consisting of non-porous short stacks of graphene sheets having a platelet shape with an average diameter d ~ 25 μm and thickness t ~ 6 nm as claimed by specification, this gives a specific surface area of 145 m²/g. The value which we measured (51 m²/g)suggests that the particles are rather made of cylinder stacks of 17 nm, i.e. a staking of 50 graphene sheets instead of only 18. The values estimated from a stack of 10 microns average diameter and 45 nm thick give a theoretical specific surface area of 19 m²/g which is coherent, taking into account the strong uncertainties in estimating the size of elementary particles by SEM.

The thermogravimetric analysis (TGA) was carried out under oxidant atmosphere. The typical characteristic plots of TGA of the fillers have been shown in Figure 4. We observed for GnP M two stages of weight loss. This behavior means that our powder sample is not homogeneous. In the first stage for GnP M the weight loss starts at about 430˚C with a maximum oxidation range of temperature of 50˚C associated with a loss of ~20% wt.

This high reactivity may be attributed to the presence of amorphous carbon. The second stage observed for GnP Mis attributed to an oxidation process of the crystalline carbon material. Nevertheless this stage occurs at higher temperature than Synthethic graphite, starting at about 726˚C and 600˚C respectively, suggesting that GnP M filler are more structured than the synthetic graphite. For synthetic graphite the maximum oxidation range of temperature is ~250˚C and this value indicate that this filler have higher polydispersity compared with GnP M which give an oxidation range of temperature ~200˚C. TGA analyses are in agreement with the results obtained by SEM image analysis.

3.2. Thermal Conductivity Results

The thermal conductivity is introduced through Fourier’s law, q = −кÑT, where q is the heat flux, к a tensor in

anisotropic materials and ÑT the temperature gradient. In the present paper small temperature variations and isotropic behavior are considered: к is treated as a constant. In graphite, heat conduction is dominated by acoustic phonons (ion-core vibrations in the hexagonal crystal structure lattice) [7] . In the graphite crystal, each atom is bonded trigonally to three others in a plane composed of strong aromatic rings due to pronounced overlap between adjacent sp² hybridized carbon and a significant weaker bond with adjacent unhybridized orbitals lying perpendicular to the plane. The resulting network is 2-dimensional and the resulting sheets are stacked through weak Van der Waals force. This implies that in-plane graphite has a higher thermal conductivity than perpendicular. Hence, in a disoriented filler composite material, the thermal conductivity results from both perpendicular and in-plane thermal conductivity. The exfoliation of graphite leads to reduce the contribution of the perpendicular conductivity and it explains the increase in thermal conductivity with the decrease of the thickness of the graphite structure or the aspect ratio.

The thermal conductivity of epoxy based composites with synthetic graphite and GnP M were compared (Figure 5). The maximum amount of GnP M filler which was possible to mix with the epoxy system carried out, is 2.67% vol. To assess the performance of the GnP M, we also prepared epoxy composites containing synthetic graphite with an aspect ratio of 8 (d ~ 13 μm, t ~ 7 μm). Figure 6 shows that the GnP M improved the thermal conductivity of the epoxy composites to 0.55 W/mK, as compared to the value of 0.18 W/mK in pristine epoxy. This thermal conductivity к₀ value is in agreement of neat epoxy system based on DGEBA or DGEBF so far reported at the exception of [15] who reported a value of 0.38 W/mK for DGEBA. Clearly, the GnP M filler provide substantially greater thermal conductivity enhancement when embedded into epoxy as compared to micronicsynthetic graphite. The high aspect ratio is apparently responsible for the improved thermal performance of the GnP M in agreement with previous works [14] .

The efficiency of the thermal filler may be characterized by the thermal conductivity enhancement (η), defined as

(1)

where к_composite is the thermal conductivity of the composite and к_epoxy is the thermal conductivity of the pristine matrix at room temperature. The increase of thermal conductivity follows approximatively linear dependence without revealing any clear signature of thermal percolation threshold since both filler and matrix contribute to the heat flow through acoustic phonons. Figure 6 shows the thermal conductivity and enhancement (η) as a function of the filler loading.

3.3. Influence of the Matrix Polymer and the Filler in the Thermal Conductivity

In the discussion of thermal properties of polymer nanocomposites, the role of the matrix properties on the overall composite is often ignored. Indeed, the thermal conductivity of the filler, the geometry, and the distribution into the polymer matrix are well established as the dominant factors that determine the thermal conductivity of epoxy composites.

Nonetheless, the polymer matrix can impact the composite thermal properties in several ways. For instance, the matrix material influences the range and strength of the interactions between filler particles [16] , so that during composite fabrication, the fillers are able to move in response to these medium-mediated interactions. These interactions impact the topology of the network structure and the thermal properties of the final composite.

How the polymer matrix alters the filler distribution and network geometry, the impact of the polymer on the thermal properties is difficult to isolate. Based on the available data from epoxy-nanoplatelet composites

reported in the literature, we summarize in the Table 2 and Table 3 some of the previously reported thermal conductivity values for epoxy resin with GnP fillers or related fillers.

Table 2 and Table 3 are not only a compilation since it was necessary for comparison purpose to estimate values. For instance, the weight fraction was converted to the volume fraction using the equation:

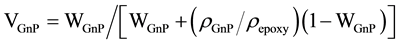(2)

V_GnP and W_GnP are the volume and weight fraction of GnP, ρ_GnP and ρ_epoxy are the densities of the GnP filler (2.3 g/cm³) and epoxy (1.2 g/cm³), respectively. The volume of the graphene unit cell is given by the equation

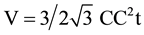(3)

C-C stands for the carbon (sp²)-carbon (sp²) bond length = 0.142 nm and t, the thickness of graphene layer,

assumed to be 0.35 nm. Since the unit cell consists of 2 carbon atoms the density of a graphene sheet can be estimated as

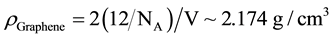(4)

N_A being the Avogadro’s number. The 2D unit cell is consequently found to lead to a density only about 0.1 g/cm³, lighter that the 3D unit cell of GnP and graphite (~2.3 g/cm³). These values agree for instance with [17] which used for the calculation of the% vol. loading: graphite and GnP: 2.26 g/cm³ and epoxy: 1.17 g/cm³.

The analysis of the data is complicated by the uncertainty in several experimental parameters such as the distribution of both thickness (degree of graphite exfoliation) and lateral size of the elementary carbon particles, the different nature of epoxy systems utilized, different mixing processing, however several facts appear. First of all, two kinds of epoxy system have been so far carried out: epoxy system based on DGEBA and DGEBF.

Bisphenol F based epoxy resins have a higher mean epoxy content per kilogram (Table 4) which induce a lower viscosity in the range of 2.5 - 4.5 Pa.s instead of 8.5 - 15 Pa.s for DGEBA.

Figure 7 highlights the fact that there are two groups of results based on the use of DGEBA and DGEBF. DGEBF offers a better medium for dispersion since up to 25% vol. of carbon fillers can be processed. Ability to incorporate fillers into a polymer matrix is never seamlessly, nanofillers being even worse. In order to help the dispersion, one strategy is to reduce the resin viscosity. The reduction in viscosity due to solvent solvating of the DGEBA molecules is often carried out. This is cited as being the key to stabilize the nanoplatelets which require sometimes to be dispersed in acetone by high shear mixing followed by bath sonication for very extended time (24 hours with sonic power 270 W [17] Table 3). However, the removal of acetone before curing has been questioned since even the presence of residual solvent alters the cross-linking process, leading to significant changes in physical, mechanical and thermal degradation properties [23] .

The data show that the measure thermal conductivity in our epoxy composites is relatively high for a resin system based on diglycidyl ether of bisphenol A (Figure 8). In this figure we report the thermal enhancement per 1% vol. filler loading. At the exception of the results of [20] with an improvement of about 350%, it appears that the use of DGEBF and DGEBA allows to reach thermal enhancement of about 170 and 50 at 1% vol. filler loading respectively.

We obtained a thermal enhancement of 66% per 1% vol. filler loading. This value is fair because micronic fillers typically show an enhancement of only ~20% per 1% vol. filler loading [6] [17] .

The thermal diffusivities published recently from DGEBA resin [19] have been converted in thermal conductivity assuming a heat capacity of 1.2 J/gK. The value obtained is in the range of the one obtained in the present work although GnPM is dispersed through a combination of ultrasonication process and three-roll milling [19] . This suggests to us that the epoxy system we carried out was more favorable than the LY556 + XB3473 system. It is obvious from Figure 7 that such strategies aiming at increasing the dispersion of the fillers within the polymer

Table 4. Chemical structure of hardeners carried out in the literature survey. Comparison of the average number of equivalent epoxy (n), the number of poly- merized subunits in the polymer resin architecture and the molecular weight by number of the resin (g/mol).

matrix lead to moderate results in comparison with the choice of the resin epoxy system. This shows that the lower molecular mass of the resin whose consequence is to reduce the viscosity is not the unique parameter. The outer thickness and lateral layers of graphite platelets and/or graphene sheets may not be easily wetted by the epoxy resin system adversely affecting the resulting composite due to poor interfacial contact. The epoxy system and its compatibility with the filler is a parameter which affects the dispersion of the fillers and might create bonds with epoxy matrix and further participate to the cross-linked structure, which could enhance the interfacial interaction between fillers and matrix improving the phonon transport in composite. Besides, such reactions with functional oxygenic groups localized on the surface of the nanoplatelets have been recently reported [21] .

Both better thermal enhancement > 66%, depicted in Figure 8 for epoxy system based on DGEBA, are obtained with natural graphite exfoliated in house after thermal shock at 1000˚C leading perhaps to a better degree of exfoliation as starting fillers. Presence of graphite ultimately exfoliated i.e. single graphene sheet and/or graphite with only 2 layers of graphene sheet should allow benefiting of the high intrinsic к_i of filler [6] . To exfoliate the GnP, ultrasonication is often carried out (Table 3). To avoid the tendency of agglomeration or re-

agglomeration three-roll milling technique is implemented and/or filler surface treatments (Table 3).

The thermal enhancement of about 350% by volume percent is rather unique in the Figure 9. One possible explanation might come from the epoxy system. On Figure 9 we report the molecular weight of the hardener carried out by each research team.

Figure 9 highlights the outstanding thermal enhancement reported by [20] . It is clear from this figure that this research team carried out an exotic epoxy system with a hardener having a molecular mass of about 30%

heavier: 4,4-Diaminodiphenyl sulfone was carried out acting as a curing agent. Although, the thermal conductivity of the neat epoxy is in the usual range of 0.2 W/mK, the thermal conductivity is boosted. This suggests that the choice of the epoxy system plays a major role in the filler ability to disperse exfoliated graphite nanoplatelets.

4. Conclusion

In summary, we report thermal properties of graphite nanoplatelets composites utilizing a simple procedure of dispersion. GnP fillers, M grade, are industrial powders with aggregates made of elementary particles presenting platelet geometry with different thickness (45 ± 14 nm) and lateral sizes (10 ± 3 µm). The composite specimens were 4 mm thick. We observe a significant increase in the thermal conductivity of the epoxy composite with the increasing graphite content characterized by a thermal enhancement of 66% per 1% vol. filler loading. Our results put into perspective with the experimental results reported or extracted from the literature suggest that the main parameter for improving thermal conductivity is the aspect ratio of the platelets. Nevertheless, the couple (epoxy system-carbon filler) is a parameter which affects the thermal conductivity by improving on one hand the loading capacity (viscosity decrease) and on the other hand the interfacial interaction between fillers and matrix improving the phonon transport in composite.

Acknowledgements

The authors would like to acknowledge Schneider Electric S.A, P.C.P Programme de Coopération Post-Gradué Pays Andins/RU2I Matériaux Nanostructurés pour un Développement Durable, and FONACIT of Venezuela for the financial support.

References

NOTES

^*Corresponding author.