Journal of Computer and Communications
Vol.03 No.09(2015), Article ID:59955,6 pages
10.4236/jcc.2015.39009
A Multi-Agent Particle Swarm Optimization for Power System Economic Load Dispatch
Chenbin Wu, Haiming Li, Lei Wu, Zhengyang Wu
Shanghai University of Electric Power, Shanghai, China
Email: wuchenbin1988@163.com, zjxulhm@163.com, wuleilei13@126.com, zenkobe24@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 August 2015; accepted 22 September 2015; published 25 September 2015
ABSTRACT
A new versatile optimization, the particle swarm optimization based on multi-agent system (MAPSO) is presented. The economic load dispatch (ELD) problem of power system can be solved by the algorithm. By competing and cooperating with the randomly selected neighbors, and adjusting its global searching ability and local exploring ability, this algorithm achieves the goal of high convergence precision and speed. To verify the effectiveness of the proposed algorithm, this algorithm is tested by three different ELD cases, including 3, 13 and 40 units IEEE cases, and the experiment results are compared with those tested by other intelligent algorithms in the same cases. The compared results show that feasible solutions can be reached effectively, local optima can be avoided and faster solution can be applied with the proposed algorithm, the algorithm for ELD problem is versatile and efficient.
Keywords:
Economic Load Dispatch, Multi-Agent System, Particle Swarm Optimization, Power System, Valve Point Effect

1. Introduction
In load planning and operation dispatching of power system, economic load dispatch (ELD) is one of the typical optimization problems. Solving this problem is one of the effective ways to improve the cost and reliability in operating of power system. The optimization objective of this problem is to reduce the cost of generation while satisfying the load demands and the operating restrictions. The relevant researches on power system reveal that the output characteristic curve of the unit is often characterized by nonlinear and non-convexity due to the valve point effect [1] of the generator units. At the same time, the cost function is different as a result of constraints on the operating conditions of the power system such as the transmission capacity limit and the system stability of the distribution network [2] . In addition, because of the large number of units in some distribution systems, the input and output characteristics of the generating units are multidimensional and have a number of local optima [3] . For realizing high accuracy in multidimensional condition, the traditional assignment optimization algorithm cannot solve the ELD optimization problems very well, such as Lagrange multiplier [4] , Quadratic programming [5] etc., more new approaches are needed.
During these days, different kinds of intelligent algorithms are widely used in ELD optimization as they have good global convergence and non-restricting by the object function, which include artificial neural network algorithm, chaos algorithm, particle swarm optimization algorithm and so on. With the constrained optimization of the non-convex nonlinear system considered, Yunhe applied the enhanced particle swarm optimization algorithm to the problem of ELD optimization successfully and proved the convergence of the algorithm in Thesis [3] . A self-adjusting particle swarm optimization algorithm was applied to ELD optimization problems by Xuewen in Thesis [6] , which overcame the premature convergence of particle swarm optimization and improved the accuracy of the optimal solution. The chaos optimization method was introduced to the ELD optimization problem in Thesis [7] .
Particle swarm optimization (PSO) was a method of biological evolution, and PSO was proposed by Kennedy and Eberhart in 1995 [8] , which had many advantages, the speed of convergence was faster, the need for the parameters was less and PSO was easy to achieve. However, when PSO is applied to an optimization problem of multidimensional and complex, it will converge too easy and fall into local optima. For this reason, significant researches have been conducted on PSO and many improved algorithms have been proposed. In this paper, we propose to use a multi-agent particle swarm optimization (MAPSO) to solve the ELD problem which has the advantages in global convergence, making the particles (as agents during iteration) to be active in locating the optimal point, and better convergence effect. It is proved successfully in comparing with other algorithms under different dimensional conditions and simulating of IEEE 3, 13 and 40 units system with valve point effect considered.
2. ELD Mathematical Model
2.1. Objection Function
The objective of the ELD is to determine the output power of generating units and to make the best generation schedule in order to meet the load demands at minimum operating cost under operating constraints. The economic load dispatch problem function:
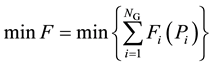 (1)
(1)
where F is total fuel cost; 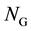 is the number of generators in the system;
is the number of generators in the system; 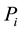 is the output active power of unit i;
is the output active power of unit i; 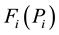 is the cost function of unit i.
is the cost function of unit i.
The generator cost function is obtained from data points taken during “heat run” tests, which is considered as a quadratic polynomial function which is formulated by:
 (2)
(2)
where ,
,  and
and  are cost coefficients of unit i.
are cost coefficients of unit i.
Because of the effect of wire drawing, which is incurred when the steam admission valve start to open, produce a rippling effect on the unit curve. This is valve point effect. If it is neglected, accuracy of the solution will be significantly affected. To model the ripples to valve point effect, equation are modified and it is represented as:
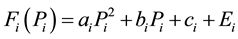 (3)
(3)
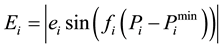 (4)
(4)
where 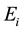 is the change influenced by valve point effect;
is the change influenced by valve point effect; 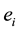 and
and 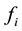 are cost coefficients of unit i while taking the valve point effect;
are cost coefficients of unit i while taking the valve point effect; 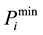 is the minimum operating output of unit i.
is the minimum operating output of unit i.
2.2. System Constraints
Generating capacity constrains can be represented as follows:
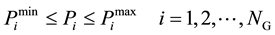 (5)
(5)
where 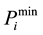 and
and 
The following is the power balance constraints:

where 

When the power system distribution network is intensively covered, 

3. Multi-Agent PSO Algorithm
3.1. PSO
The particle swarm optimization is an intelligent algorithm based on biological evolution. Each member of the population is called a particle, which represents a potential solution to the optimization problem. And the position of the food is considered to be the global optimal solution. All individuals search the global optimal solution in the solution space, and each particle has a fitness function value and speed to adjust its own direction of movement. In the process of searching food, all particles in the population have the capacity of memory, they can adjust their own position and the best position they had experienced. In order to achieve the purpose of finding the location of food, each particle through continuous learning to their own best location and the best position of the whole population, and ultimately access to the food. In other words, particles have the ability of self-perception and social learning.
The PSO algorithm begins by initializing a group of random particles, which can find the optimal solution through an iterative process. Each particle adjusts its position in term of its own experience, and the experience of its neighborhood particles. The best position of itself is called Pbest, and the best position of its neighborhood is called Gbest.


where, x means the current position of particles, and v means the current velocity of particles. i and j mean the j-th dimension of the i-th particle. s and w are set as the current number of iterations and the weight parameter, respectively, and we set c as the learning factor and r is a random number between 0 and 1.
Formula (8) is the speed function, by which each particle update their own pace according to the optimal solution Pbest and Gbest in the iterative process. Formula (9) is the location function; it means that particles update their position and got the optimal solution after numbers of iteration.
3.2. Multi-Agent System
In the multi-agent system (MAS) [9] , agent is a kind of intelligent and computational system with the ability of perception, problem-solving, and can communicate and interact with other systems for achieving goals together. Agent usually has the following typical characteristics:
1) Agent is usual in a particular environment, and only work in that environment.
2) Agent can sense the local environment where they are in.
3) Agent has a good ability of autonomy, which can complete its specific task independently without external intervention.
4) Agent should have the ability to respond about the environment and make the appropriate action.
3.3. MAPSO
MAPSO is a new algorithm, which combines PSO and the main features of MAS [10] . At first, we construct an agent living environment; each agent can not only compete and cooperate with its neighbors but also complete self-learning. What’s more, it can absorb the evolutionary mechanism of PSO. Sharing information from the globally optimal agent and correcting action strategies based on their own experiences, which make it converge to the global optimal solution quickly and accurately. For overcoming the difficulties of different ELD problems, the appropriate improvements and adjustments are done in the programming.
1) Definition of agent intentions
In MAPSO algorithm, any agent is considered as


The purpose is to minimize their fitness with the restrictions under operating conditions. For that purpose, agent will make the appropriate response according to their environment to reduce its fitness.
2) Definition of environment
In order to definite the environment simply, a lattice structure environment has been designed. Each agent lives in this environment, and is fixed at one grid. Each circle represents an agent; data in circle represent the agent location in the environment. Each agent should contain two values that are equal to the speed and position in PSO algorithm. 


3) Definition of local environment
In the MAS system, defining the local environment is very important because agent usually senses the information in local environment and takes an action strategy to complete its intent and purpose. Assumptions 



4) Agent move strategies
At first, every agent competes and cooperates according to their local environment and neighbors. Assume
that the agent is 





If 

where, 






5) Agent self-learning operation
Agent not only competes and cooperates in their local environment, but also possesses knowledge by its own self-study, to improve the ability to solve problems. From past articles, we know that small range of genetic algorithms have a good effect on its local searching ability. Inspired by this method, in this paper small range of search techniques are applied to achieve agent self-learning function.
4. Analysis of cases
In order to demonstrate the performance of the proposed MAPSO method for solving the effectiveness of high- dimensional, non-convex, non-conducting and multi-constrained optimization problems, the proposed algorithm is tested on three different dimensions typical ELD problems. All the test cases consist of valve-point loading effects of the ripple curve and the transmission loss is neglected. In this section, MAPSO method will be tested by simulation using MATLAB 8.1, and the results will be compared with other intelligent algorithms [11] -[15] , such as IGA, MPSO, and CEP. All the parameters of generators in cases below can be obtained from reference [15] . In the different cases, we tested the algorithm 100 times separately under the same condition, the average cost (Fmean), the minimum cost (Fmin), and the maximum cost (Fmax) are acquired from the tests, and the results from other algorithms can be acquired from the references.
Case 1: In this section, MAPSO method is applied to a 3-generator system with 6 bus bars by simulation. The expected load demand for this test case is equal to 850 MW. The values of population size, neighbor size and dimension are 64, 20 and 3 respectively. Different methods tested on the same system are compared and the convergence characteristics are shown and illustrated in Figure 1 and Table 1.
In Figure 1, it can be seen that the MAPSO converges faster. In Table 1, MAPSO algorithm cost less compared to other intelligent algorithms in references.
Case 2: The proposed method is also tested on the 13-unit system. In difference, the expected load demand for this test case is 1800 MW, and the dimension is 13. Other parameters are the same with Case 1. The simulation results are shown in Figure 2, the comparison of the convergence characteristics of various methods is illustrated in Table 2, and different methods tested on the same system are also compared and illustrated in Table 2.
As seen in Figure 2, the convergence rate of MAPSO algorithm is faster if the dimension is higher. Comparison of the data in Table 2 reveals that the optimal solution and reliability of MAPSO algorithm are better than other intelligent algorithms.
Case 3: The third test system consists of 40 thermal generating units. The expected load demand for this test case is equal to 10,500 MW, and the dimension is 40. Other parameters are the same with Case 1. Figure 3 demonstrates the convergence characteristics and Table 3 presents the results in comparison with the other approaches available in the literature.
Table 1. Results comparison of Case 1.
Table 2. Results comparison of Case 2.
Table 3. Results comparison of Case 3.
Figure 1. Convergence comparison of MAPSO and PSO in this Case 1.
Figure 2. Convergence comparison of MAPSO and PSO in this Case 2.
Figure 3. Convergence comparison of MAPSO and PSO in this Case 3.
It is notable that the ability of the MAPSO in finding the optimization solution is an efficient method in Figure 3. In comparison with the other intelligent algorithms in Table 3 shows that MAPSO performed better, indicating that the algorithm has better results on multidimensional problems, and can be applied to engineering practice.
In conclusion form three cases above, MAPSO outperformed both accuracy and convergence speed of solution. No matter the dimension is lower or higher, MAPSO has good reliability. With its advantages, the MAPSO algorithm is a good choice for computing the optimization problems of ELD in large power systems.
5. Conclusion
A versatile optimization algorithm MAPSO is proposed in this paper, by which different dimensional and non- convex and nonlinear constraints problems in ELD can be solved successfully. As traditional PSO and other intelligent algorithms, MAPSO algorithm is simple and easy to program. But the difference is that MAPSO overcomes the shortcomings of easily falling into local optima, and achieves the goal of high convergence precision and speed. Tests are done in this paper with considering the valve point effect, line capacity and constraints of generator units. The result of the experiments demonstrates that ELD can be solved by MAPSO with faster speed than other evolutionary algorithms. The proposed algorithm also can be used to solve other power system optimization problems with different dimensional, nonlinear, non-conductive characteristics. The MAPSO algorithm will have a widely application prospects in the future.
Cite this paper
ChenbinWu,HaimingLi,LeiWu,ZhengyangWu, (2015) A Multi-Agent Particle Swarm Optimization for Power System Economic Load Dispatch. Journal of Computer and Communications,03,83-89. doi: 10.4236/jcc.2015.39009
References
- 1. David, C.W. and Gerald, B.S. (1993) Genetic Algorithm Solution of Economic Dispatch with Valve Point Loading. IEEE Transactions on Power Systems, 8, 1325-1332.
http://dx.doi.org/10.1109/59.260861 - 2. Wheimin, L., Fusheng, C. and Mingtong, T. (2001) Non-Convex Economic Dispatch by Integrated Artificial Intelligence. IEEE Transactions on Power Systems, 16, 307-311.
http://dx.doi.org/10.1109/59.918303 - 3. Hou, Y.H., Lu, L.J., Xiong, X.Y., et al. (2004) Enhanced Particle Swarm Optimization Algorithm and Its Application on Economic Dispatch of Power Systems. Proceedings of the CSEE, 24, 95-100. (In Chinese)
- 4. Wang, S.J., Shahidehpour, S.M. and Kirschen, D.S. (1995) Short-Term Generation Scheduling with Transmission and Environmental Constraints Using an Augmented Lagrangian Relaxation. IEEE Transactions on Power Systems, 10, 1294-1301. http://dx.doi.org/10.1109/59.466524
- 5. Fan, J.-Y. and Zhang, L. (1998) Real-Time Economic Dispatch with Line Flow and Emission Constrains Using Quadratic Programming. IEEE Transactions on Power Systems, 13, 320-325.
http://dx.doi.org/10.1109/59.667345 - 6. Zhang, X.W. and Li, Y.J. (2006) Self-Adjusted Particle Swarm Optimization Algorithm Based Economic Load Dispatch of Power System. Power System Technology, 30, 8-13. (In Chinese)
- 7. Tang, W. and Li, D.P. (2000) Chaotic Optimization for Economic Dispatch of Power Systems. Proceedings of the CSEE, 20, 36-40. (In Chinese)
- 8. Kennedy, J. and Eberhart, R.C. (1995) Particle Swarm Optimization. Proceeding of the 1995 IEEE International Conference on Neural Network. Perth, 27 November-1 December 1995, 1942-1948.
http://dx.doi.org/10.1109/icnn.1995.488968 - 9. Wooldridge, M. (2002) An Introduction to Multi-Agent System. Wiley, New York.
- 10. Zhong, W.C., Liu, J., Xue, M.Z. and Jiao, L.C. (2004) A Multi-Agent Genetic Algorithm for Global Numerical Optimization. IEEE Transactions on Systems, Man, and Cybernetics, 34, 1128-1141.
http://dx.doi.org/10.1109/TSMCB.2003.821456 - 11. Wang, X., Wang, X., Li, L.X., et al. (2013) Reactive Power Optimization for Wind Power System Based on Dynamic Cloud Evolutionary Particle Swarm Optimization. Power System Protection and Control, 41, 36-43. (In Chinese)
- 12. Liu, H. and Liu, Z.G. (2015) An Improved Particle Swarm Algorithm Study on Optimization Model of Maintenance Schedules for Railway Traction Substations. Power System Protection and Control, 43, 87-94. (In Chinese)
- 13. Ling, S.H., Lam, H.K., Leung, F.H.F. and Lee, Y.S. (2003) Improved Genetic Algorithm for Economic Load Dispatch with Valve-Point Loadings. The 29 Annual Conference of the IEEE Industrial Elec-tronics Society, 1, 442-447.
- 14. Park, J.-B., Lee, K.-S., Shin, J.-R. and Lee, K.Y. (2003) Economic Load Dispatch for Non-Smooth Cost Functions Using Particle Swarm Optimization. 2003 IEEE Power Engineering Society General Meeting, 2, 938-943.
- 15. Sinha, N., Chakrabarti, R. and Chattopadhyay, P.K. (2003) Evolutionary Programming Techniques for Economic Load Dispatch. IEEE Transactions on Evolutionary Computation, 7, 83-94.
http://dx.doi.org/10.1109/TEVC.2002.806788





