ABSTRACT

The aim of this paper is to present a numerical study of oscillatory motion of Oldroyd-B fluid in a uniform magnetic field through a small circular pipe. First, we derive the orientation stress tensor by considering the Brownian force. Then, the orientation stress tensor is incorporated by taking Hookean dumbbells on Brownian configuration fields in the Oldroyd-B model. The Oldroyd-B model is then reformulated coupled with the momentum equation and the total stress tensor. Finally, we analyze the orientation stress tensor in the pipe by the numerical simulations of the model and showed that the effect of orientation stress tensor is considerable although the Brownian force is sufficiently small.

Keywords:

Oldroyd-B Fluid, Brownian Force, Finite Difference, Oscillatory Flows

1. Introduction

The theory of Newtonian fluids well enough describes the mechanical behavior of many real fluids. But still we have a lot of fluids which are not properly entertained by Newtonian fluid such as ketchup, blood, paints, shampoo, pulps, honey, oil and drilling mud etc. In general, these fluids are known as non Newtonian fluids. As we know, these fluids are commonly used in daily life and have many applications toward industries as well as to academics. Many researchers have attempted to develop a single model which represents all these fluids but they haven’t found any success in their struggle. Consequently, different fluids model have been proposed for these fluids. Which are commonly divided into three main classes namely, fluids of differential type, integral type and rate type. The rate type models are considered to be much more practical and important. One of the famous rate type model is Maxwell fluids [1] , considered to be the first rate type model. This model is still very attractive for the researchers. Rajagopal [2] formulated a formal thermodynamic framework based on the seminal work of Maxwell, for different class of fluids. Among them is Oldroyd-B model, which is considered to be the more generalized fluid model as it deals with relaxation as well as retardation times. Most of the fluids are particular cases of Oldroyd-B fluid.

In the last few decades, oscillating bodies have widely studied due to importance in practical fields and experiments. They are considered in various biological and industrial processes, for example in nuclear reactor, oil exploitation, the periodicity of blood flow [3] , food industry, bio-engineering and chemistry, cellulose and soap solutions etc. Also, magnetohydrodynamics (MHD) flows plays an important role in development of energy generation and in the dynamics of geophysical and astrophysical fluid. In the last few years researchers contribute alot on MHD flow, see [4] [5] [6] [7] and reference therein.

In this paper, we developed an Oldroyd-B model by taking a total stress tensor which consists of the shear stress tensor, the orientation stress tensor (OST) and isotropic pressure stress tensor. The model deals with the dynamics of oscillatory flow of Oldroyd-B fluid inside a circular pipe. Continuity and momentum equations along with Oldroyd-B model have been taken under consideration. The whole system is then reformulated along with the total stress tensor. Finally, we solve numerically by employing the finite-difference scheme for the Oldroyd-B model and orientation stress tensor. Our numerical results show that in spite the Brownian force is very small still the effect of the orientation stress tensor on the Oldroyd-B model is considerable.

2. Reformulation of Oldroyd-B Model

In this section, we incorporate a Brownian force when MHD flow of Oldroyd-B fluid is passing through a pipe. To do this we consider the orientation stress tensor $S$ for time-dependent incompressible flow [3] :

$\frac{\partial S}{\partial t}+\left(\upsilon \cdot \nabla \right)S-S\nabla \upsilon -{\left(\nabla \overrightarrow{\upsilon }\right)}^{\text{T}}S=-\frac{1}{\tau }\left(S-\frac{\alpha \left(t\right)}{{\left(6\text{π}\eta a\right)}^2}I\right)\mathrm{,}$ (1)

for some $\alpha \left(t\right)\ge 0$ , here $2k\Gamma /\text{π}\eta a^3={\tau }^{-1}$ is the dumbbell inverse relaxation time, a is the radius of bead, $\Gamma =37˚\text{C}$ is the temperature, $k\left(=1.38\times {10}^{-23}{\text{m}}^2\cdot \text{kg}\cdot {\text{s}}^{-2}\cdot {\text{K}}^{-1}\right)$ is the Boltzmann constant, $\eta$ is the viscosity of fluid and $\upsilon$ is the velocity. Equation (1) will be used to reformulate the Oldroyd-B model. Many researchers [8] [9] [10] [11] have developed their models by taking a total stress tensor which consists of the shear and isotropic pressure stress tensors without considering the orientation stress tensor. Here, we extend our model by taking the shear and isotropic pressure stress tensors as well as orientation stress tensor with a constant g (the elastic modulus). Let $\sigma$ be the total stress tensor and $\upsilon =\left(v_1,v_2,v_3\right)$ be the velocity of the MHD flow. For the unsteady incompressible flow the continuity and the momentum equations are given by:

$\begin{array}{l}\nabla \cdot \upsilon =0,\\ \rho \left(\frac{\partial \upsilon }{\partial t}+\upsilon \cdot \nabla \upsilon \right)=-Nv+div\left(\sigma \right),\\ \sigma =gS+\eta \left(\nabla \upsilon +{\left(\nabla \upsilon \right)}^{\text{T}}\right)-pI,\end{array}$ (2)

where $N=\delta {\beta }_o$ , in which the magnitude of a uniform magnetic field is denoted by ${\beta }_o$ and the direction of uniform magnetic field is normal to the motion of fluid, $\delta$ is the fluid electrical conductivity, $\rho$ is the density of fluid, $\eta$ is the fluid viscosity, identity matrix is represented by $I$ , $S$ is the orientation stress tensor, elastic modulus is represented by g and- $pI$ represents the isotropic pressure stress tensor.

Now, we reformulate the Oldroyd-B model by supposing $L=\nabla \upsilon$ , $A=L+L^{\text{T}}$ , $D=\eta A+gS$ and combining it with the momentum equation and Equation (1)

$\begin{array}{l}D+{\alpha }_1\left[\frac{\text{d}}{\text{d}t}D-LD-D{L}^{\text{T}}\right]\\ =\eta \left[A+{\alpha }_2\left(\frac{\text{d}}{\text{d}t}A-LA-A{L}^{\text{T}}\right)\right]+gS-\frac{{\alpha }_{2}g}{\tau }\left(S-\frac{\alpha \left(t\right)}{{\left(6\text{π}\eta a\right)}^2}I\right),\end{array}$ (3)

where $\text{d}/\text{d}t$ is the material derivative, ${\alpha }_1$ and ${\alpha }_2$ represents the material constants.

Let $x=\left(x_1,x_2,x_3\right)$ , $v\left(x,t\right)=\left(v_1,v_2,v_3\right)$ is the velocity and

$S\left(x,t\right)=\left[\begin{array}{ccc}{S}_{11}& S_{12}& S_{13}\\ S_{21}& S_{22}& S_{23}\\ S_{31}& S_{32}& S_{33}\end{array}\right]$ (4)

is the orientation stress tensor which is considered to be symmetric [12] - [20] . The total stress tensor consists of nine components are given by

${\sigma }_{st}=-p{I}_{st}+\eta \left(\frac{\partial {\upsilon }_s}{\partial x_t}+\frac{\partial {\upsilon }_t}{\partial x_s}\right)+g{S}_{st},\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{for}s,t=1,2,3.$ (4a)

To obtain the components of the OST $S$ , first we determine all the nine components of the OST $S$ from Equation (4) then we solve the reformulated Oldroyd-B model to get all these nine components:

$\begin{array}{l}{D}_{ij}+{\alpha }_1\left[\frac{\partial D_{ij}}{\partial t}+{\displaystyle \sum _{k=1}^3}\left(v_k\frac{\partial D_{ij}}{\partial x_k}-D_{ik}\frac{\partial v_j}{\partial x_k}-D_{kj}\frac{\partial v_i}{\partial x_k}\right)\right]\\ =\eta \left[A_{ij}+{\alpha }_2\left[\frac{\partial A_{ij}}{\partial x_t}+{\displaystyle \sum _{k=1}^3}\left(v_k\frac{\partial A_{ij}}{\partial x_k}-A_{ik}\frac{\partial v_j}{\partial x_k}-A_{kj}\frac{\partial v_i}{\partial x_k}\right)\right]\right]\\ +g{S}_{ij}-\frac{{\alpha }_2}{\tau }\left(S_{ij}-\frac{\alpha \left(t\right){\delta }_{ij}}{{\left(6\text{π}\eta a\right)}^2}I\right),i,j=1,2,3.\end{array}$ (5)

Here, Kronecker delta is represented by ${\delta }_{ij}$ . Pressure p will be obtained by substituting all those nine components of $S$ in the momentum equation.

$\begin{array}{l}\rho \frac{\partial {\upsilon }_i}{\partial t}+\rho {\displaystyle \sum _{j=1}^3}{\upsilon }_j\frac{\partial {\upsilon }_i}{\partial x_j}\\ =-\frac{\partial p}{\partial x_i}-N{v}_i+\eta \left[{\displaystyle \sum _{j=1}^3}\left(\frac{{\partial }^2{\upsilon }_i}{\partial x_j^2}+\frac{{\partial }^2{\upsilon }_j}{\partial x_i\partial x_j}\right)\right]+g{\displaystyle \sum _{j=1}^3}\frac{\partial S_{ij}}{\partial x_j},i,j=1,2,3.\end{array}$ (6)

Then we substitute the OST $S$ and the pressure p in Equation (4a) to get the total stress tensor $\sigma$ .

3. Total Stress Tensor

To find the numerical solution we use an iterative method. Several mixed and semi-implicit methods have been proposed to get more efficient solvers while preserving stability. We take velocity as

$\upsilon \left(x,t\right)=\left(u\cos \left(\omega t\right)x_1,0,0\right),$

where $u$ is the amplitude of the velocity and $\omega$ is the frequency. The appropriate conditions of velocity are:

$\begin{array}{l}\upsilon \left(x,0\right)=0,0<x_1\le 0.\\ \upsilon \left(0,t\right)=0,t\ge 0.\\ \frac{\partial \upsilon \left(x,t\right)}{\partial x_1}=0,x_1=r.\end{array}$ (7)

where r is the radius of the pipe. For the sake of simplification we neglect some of the components of the OST by taking $S_{22}=S_{33}=S_{23}\simeq 0$ . Thus, Equation (6) becomes

$\begin{array}{l}\frac{\partial S_{11}}{\partial t}+u\cos \left(\omega t\right)x_1\frac{\partial S_{11}}{\partial x_1}-2u\cos \left(\omega t\right)S_{11}\\ =\eta \frac{\left({\alpha }_2-{\alpha }_1\right)}{{\alpha }_{1}g}\left(2u\omega \sin \left(\omega t\right)-2u\cos {\left(\omega t\right)}^2\right)-\frac{{\alpha }_2}{g{\alpha }_1\tau }\left(S_{11}-\frac{\alpha \left(t\right)}{{\left(6\text{π}\eta a\right)}^2}\right),\\ \frac{\partial S_{12}}{\partial t}+u\cos \left(\omega t\right)x_1\frac{\partial S_{12}}{\partial x_1}-2u\cos \left(\omega t\right)S_{12}=-\frac{{\alpha }_2}{g{\alpha }_1\tau }{S}_{12},\\ \frac{\partial S_{13}}{\partial t}+u\cos \left(\omega t\right)x_1\frac{\partial S_{13}}{\partial x_1}-2u\cos \left(\omega t\right)S_{13}=-\frac{{\alpha }_2}{g{\alpha }_1\tau }{S}_{13}.\end{array}$ (8)

Similarly Equation (7) becomes

$\begin{array}{l}\rho u\omega sin\left(\omega t\right)x_1+\rho {\left(ucos\left(\omega t\right)\right)}^2{x}_1\\ =-\frac{\partial p}{\partial x_1}-Nucos\left(\omega t\right)x_1+g\frac{\partial S_{11}}{\partial x_1}\mathrm{.}\end{array}$ (9)

To get solution of Equation (6), we need to find the component $S_{11}$ of OST and pressure p with and without OST.

$\begin{array}{l}\frac{\partial S_{11}}{\partial t}+u\cos \left(\omega t\right)x_1\frac{\partial S_{11}}{\partial x_1}-2u\cos \left(\omega t\right)S_{11}\\ =\eta \frac{\left({\alpha }_2-{\alpha }_1\right)}{{\alpha }_{1}g}\left(2u\omega \sin \left(\omega t\right)-2u\cos {\left(\omega t\right)}^2\right)-\frac{{\alpha }_2}{g{\alpha }_1\tau }\left(S_{11}-\frac{\alpha \left(t\right)}{{\left(6\text{π}\eta a\right)}^2}\right),\\ \rho u\omega \sin \left(\omega t\right)x_1+{\left(u\cos \left(\omega t\right)\right)}^2{x}_1=-\frac{\partial p}{\partial x_1}-Nu\cos \left(\omega t\right)x_1+g\frac{\partial S_{11}}{\partial x_1},\\ \rho u\omega \sin \left(\omega t\right)x_1+{\left(u\cos \left(\omega t\right)\right)}^2{x}_1=-\frac{\partial p}{\partial x_1}-Nu\cos \left(\omega t\right)x_1.\end{array}$ (10)

To solve the above system we use the following values for different parameters:

$\rho =1.024\times {10}^3\text{kg}\cdot {\text{cm}}^{-3}$ , $u=0.5\text{kg}\cdot {\text{cm}}^{-2}\cdot {\text{s}}^{-2}$ , $g=1.13616\text{dyn-cm}$ , $\eta =5.0380P$ , $N=2.53\text{N}\cdot \text{s}\cdot {\text{cm}}^{-1}$ and $\omega =7.2\text{Hz}$ . The components of total stress tensor $\sigma$ can be obtained from the pressure and from the corresponding components of OST. All the nine components of the total stress tensor are given by

$\begin{array}{l}{\sigma }_{11}=-p\left(t,x_1\right)+2\eta u\cos \left(\omega t\right)+g{S}_{11}\left(t,x_1\right),\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}{\sigma }_{22}={\sigma }_{33}=-p,\\ {\sigma }_{12}={\sigma }_{13}={\sigma }_{21}={\sigma }_{31}=g{S}_{12}\left(t,x_1\right),\mathrm{<mi>\; </mi>\; <mi>\; </mi>}{\sigma }_{32}=0={\sigma }_{23}.\end{array}$ (11)

4. Numerical Results and Discussion

Some 3D surfaces are presented here to show the components of OST and the effect of OST on total stress tensor. Figure 1 and Figure 2 shows the components of orientation stress tensor. The component $S_{11}$ with the configuration of Brownian force is depicted in Figure 1. The components $S_{12}$

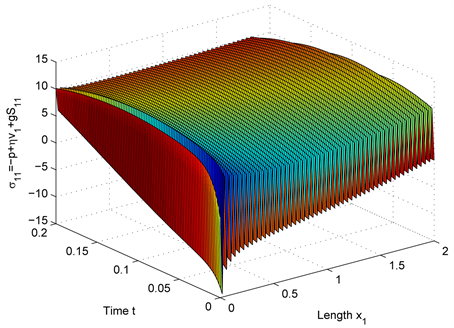
and $S_{13}$ are similar and since S is symmetric so $S_{21}=S_{12}=S_{13}=S_{31}$ . In Figure 2 we have shown the components $S_{12}=S_{13}$ . All the remaining components of S are taken to be zero. Figure 1 and Figure 2 shows that all the components of OST are not similar. Figure 3 shows the component ${\sigma }_{11}$ of total stress tensor with the OST $S_{11}$ , which is the numerical result of the system (11). We solve system (11) numerically for component $S_{11}$ and for pressure p with the OST, and then by putting $S_{11}$ and p in Equation (5) we get the component ${\sigma }_{11}$ of

total stress tensor with OST. In system (11) in the absence of OST we solve for p, and by substituting it in Equation (5) we get the component ${\sigma }_{11}$ of total stress tensor without the OST component $S_{11}$ and is depicted in Figure 4. In Figure 5 we show the total stress tensor with and without the OST. From the figure it is obvious that inspite the Brownian force is very small still the effect of the OST is

considerable. Note that we take only the $x_1$ -axis of velocity for numerical results, which shows that the magnitudes of all of the components of stress are not similar. Hence, from these figures we can examine all the results and can find the impact of total and OST as well as the effect of pressure quantitatively on the phenomena of flow in order to confirm the validity of the said Oldroyd-B model.

Special Cases. The similar solutions for Newtonian, Maxwell and second grade fluids performing the same motion are obtained here as limiting cases of the solutions. In the absence of the OST the Oldroyd-B model in the system (6) is reduced to the following model:

1) Taking ${\alpha }_1=0$ and ${\alpha }_2\ne 0$ , model for Newtonian fluid is obtained.

2) Taking ${\alpha }_1\to 0$ and ${\alpha }_2\ne 0$ , then the model is simplified to Maxwell model.

3) Taking ${\alpha }_1\ne 0$ and ${\alpha }_2\to 0$ , the model reduced to second-order fluid.

5. Conclusion

In this article, we presented oscillatory motion of Oldroyd-B fluid in a uniform magnetic field using numerical scheme. The fluid is passing through a small circular pipe. Taken into consideration the Brownian force, we derive the orientation stress tensor. Then, the orientation stress tensor is incorporated by taking Hookean dumbbells on Brownian configuration fields in the Oldroyd-B model. The reformulated Oldroyd-B model has been obtained with the help of momentum equation and the total stress tensor equation. At the end, the orientation stress tensor has been analyzed by the numerical simulations of the model which shows that the effect of orientation stress tensor is considerable although the Brownian force is sufficiently small.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (11571378).

Cite this paper

Khan, A., Zaman, G., Li, Y., Ahmad, S. and Hussain, A. (2017) The Oscillatory Motion of Oldroyd-B Fluid by Incorporating Some of the Mechanical Factors. Journal of Applied Mathematics and Physics, 5, 2402-2410. https://doi.org/10.4236/jamp.2017.512196

References