Journal of Applied Mathematics and Physics
Vol.04 No.11(2016), Article ID:72402,10 pages
10.4236/jamp.2016.411206
An Alternating Direction Nonmonotone Approximate Newton Algorithm for Inverse Problems
Zhuhan Zhang, Zhensheng Yu, Xinyue Gan
University of Shanghai for Science and Technology, Shanghai, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 28, 2016; Accepted: November 27, 2016; Published: November 30, 2016
ABSTRACT
In this paper, an alternating direction nonmonotone approximate Newton algorithm (ADNAN) based on nonmonotone line search is developed for solving inverse problems. It is shown that ADNAN converges to a solution of the inverse problems and numerical results provide the effectiveness of the proposed algorithm.
Keywords:
Nonmonotone Line Search, Alternating Direction Method, Bound-Constraints, Newton Method

1. Introduction
We consider inverse problems that can be expressed in the form
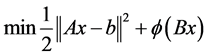 , (1)
, (1)
where 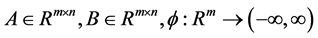 is convex, and
is convex, and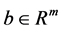 . The emphasis of our work is on problems where A and B have a specific structure. It can be applied to many applications, especially in machine learning [1] [2] , image reconstruction [3] [4] or model reduction [5] . We assume that the functions in (1) are strictly convex, so both problems has an unique solution
. The emphasis of our work is on problems where A and B have a specific structure. It can be applied to many applications, especially in machine learning [1] [2] , image reconstruction [3] [4] or model reduction [5] . We assume that the functions in (1) are strictly convex, so both problems has an unique solution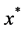 .
.
In Hong-Chao Zhang’s paper [6] , he uses the Alternating Direction Approximate Newton method (ADAN) based on Alternating Direction Method (ADMM) which originaly in [7] to solve (1). He employs the BB approximation to increase the iterations. In many applications, the optimization problems in ADMM are either easily resolvable, since ADMM iterations can be performed at a low computational cost. Besides, combine different Newton-based methods with ADMM have become a trend, see [6] [8] [9] , since those methods may achieve the high convergent speed.
In alternating direction nonmonotone approximate Newton (ADNAN) algorithm developed in this paper, we adopt the nonmonotone line search to replace the traditional Armijo line search in ADAN, because the nonmonotone schemes can improve the likelihood of finding a global optimum and improve convergence speed in cases where a monotone scheme is forced to creep along the bottom of a narrow curved valley in [10] .
In the latter context, the first subproblem is to solve the unconstrained minimization problems with Alternating Direction Nonmonotone Approximate Newton algorithm. The purpose is to accelerate the speed of convergence, and then to project or the scale the unconstrained minimizer into the box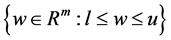 , The second subproblem is a bound-constrained optimization problem.
, The second subproblem is a bound-constrained optimization problem.
The rest of the paper is organized as follows. In Section 2, we give a review of the alternating direction approximate Newton method. In Section 3, we introduce the new algorithm ADNAN. In Section 4, we introduce the gradient-based algorithm of the second subproblem. A preliminary convergence analysis for ADNAN and gradient- based algorithm (GRAD) is given in Section 5. Numerical results presented in Section 6 explain the effectiveness of ADNAN and GRAD.
2. Review of Alternating Direction Approximate Newton Algorithm
In this section, we briefly review the well-known Alternating Direction Approximate Newton (ADAN) method which has been studied in the areas of convex programming and image reconstruction see [4] [6] and references therein.
We introduce a new variable w to obtain the split formulation of (1):
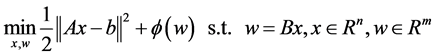 (2)
(2)
The augmented Lagrangian function associated with (2) is
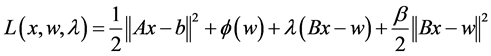 (3)
(3)
where 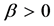 is the penalty parameter,
is the penalty parameter, 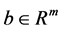 is a Lagrangian multiplier associated with the constraint
is a Lagrangian multiplier associated with the constraint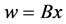 . In ADMM, each iteration minimizes over x holding w fixed, minimizes over w holding x fixed, and updates an estimate for the multiplier b. More specifically, if
. In ADMM, each iteration minimizes over x holding w fixed, minimizes over w holding x fixed, and updates an estimate for the multiplier b. More specifically, if 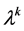 is the current approximation to the multiplier, then ADMM [10] [11] applied to the split formulation (3) is given by the iteration:
is the current approximation to the multiplier, then ADMM [10] [11] applied to the split formulation (3) is given by the iteration:
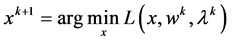 (4)
(4)
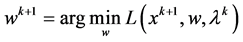 (5)
(5)
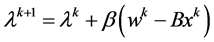 (6)
(6)
And (4) can be written as follows:
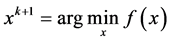
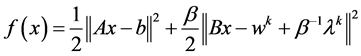 (7)
(7)
For any Hermitian matrix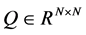 , we define
, we define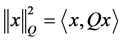 , if Q is a positive definite matrix, then
, if Q is a positive definite matrix, then 

In ADAN, the choice 











Here, 










and 







Note that by substituting 


The inner product between 


It follows that 



where
In this section, we adopt a nonmonotone line search method [9] . The step size 
Initialization: Choose starting guess






Convergence test: If 
line search update: set



or the (nonmonotone) Armijo conditions:



Cost update: Choose

Observe that 






then 

scheme with 



Lemma 2.1 If 




3. Alternating Direction Nonmonotone Approximate Newton Algorithm
In Algorithm 1, we could get the x at each iteration which can be combined with Algorithm 2. Then, we use the Algorithm 2 to solve the first subproblem in this paper which is an unconstrained minimization problem with ADNAN, then to project or the scale the unconstrained minimizer into the box

the iteration is as follows:



Later we give the existence and uniqueness result for (1).
The solution 
with P being the projection map onto the box
Algorithm 2. Alternating Direction Nonmonotone Approximate Newton algorithm.
Parameter:
Step 1: If 


Step 2: If 
Step 3: If 
Step 4: Update x which generated from Algorithm 1.
Step 5:
Step 6:
Step 7: If a stopping criterion is satisfied, terminate the algorithm, Otherwise k = k + 1 and go to Step 1.
Lemma 3.1: we show some criteria that are only satisfied a finite number of times, so 

Uniformly in k, we have 




Lemma 3.2: If

4. Algorithm 3: Gradient-Based Algorithm (GRAD)
Next, we consider the second subproblem which is about bound-constrained optimization problem as

And the iteration is similar with (4) (5) (6) as follows:



Compute the solution 
Compute the solution 
Set
5. Convergence Analysis
In this section, we show the convergence of proposed algorithms. Obviously, the proofs of the two algorithms are almost the same, and we only prove the convergence of algorithm 2.
Lemma 3.1: Let L be the function in (3). The vector 


Lemma 3.2: Let L be the function in (3), 
the sequence 

Theorem 3.1: Let 
then


Proof From Lemma 3.1, 3.2, we obtain that

Since we have a unique minimizer in


6. Numerical Experiments
6.1. Parameter Settings
In Algorithm 2, the parameters




The search directions were generated by the L-BFGS method developed by No-cedal in [16] and Liu and Nocedal in [1] . We choose the step size 

In addition, we timed how long it took ADNAN to reduce the objective error to within 1% of the optimal objective value. The algorithms are coded in MATLAB, version 2011b, and run on a Dell version 4510U with a 2.8 GHz Intel i7 processor.
In Algorithm 3, a 256-by-256 gray-scale image was considered, which is compared to the experiment by J. Zhang [8] . The dimensions of the inverse problems are m = n = 65536 and the constraints are 

6.2. Experiments Results
This section compares the performance of the ADNAN to ADAN. The main difference between the ADNAN algorithm and the ADAN algorithm is the computation of






The initial guess for



Figure 1.
Figure 2.
Figure 3.
On the other hand, the experiment results about Algorithm 3 are as follows:
Original image blurry image deblurred image
Figure 4.
Original image blurry image deblurred image
Figure 5.
Original image blurry image deblurred image
Figure 6.
Original image blurry image deblurred image
Figure 7.
7. Conclusions
According to the Figures 1-3, we can conclude that the nonmonotone line search could accelerate the convergence speed, furthermore ADNAN could get the objective values more stable and fast during the iterations when compared to ADAN.
On the other hand, the validness of GRAD is verified. Experiments results on image deblurring problems in Figures 4-7 show that difference constraints on x can also get effective deblurred images.
Acknowledgements
This work is supported by Innovation Program of Shanghai Municipal Education Commission (No. 14YZ094).
Cite this paper
Zhang, Z.H., Yu, Z.S. and Gan, X.Y. (2016) An Alternating Direction Nonmonotone Approximate Newton Algorithm for Inverse Problems. Journal of Applied Mathematics and Physics, 4, 2069- 2078. http://dx.doi.org/10.4236/jamp.2016.411206
References
- 1. Amit, Y. (2007) Uncovering Shared Structures in Multiclass Classification. Machine Learning, Twenty-fourth International Conference, 227, 17-24.
https://doi.org/10.1145/1273496.1273499 - 2. Argyriou, A., Evgeniou, T. and Pontil, M. (2007) Multi-Task Feature Learning. Advances in Neural Information Processing Systems, 19, 41-48.
- 3. Chambolle, A. (2004) An Algorithm for Total Variation Minimization and Applications. Journal of Mathematical Imaging and Vision, 20, 89-97.
- 4. Chambolle, A. (2011) A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging. Journal of Mathematical Imaging and Vision, 40, 120-145.
- 5. Zhang, L. and Vandenberghe, L. (2009) Interior-Point Method for Nuclear Norm Approximation with Application to System Identification. SIAM Journal on Matrix Analysis and Applications, 31, 1235-1256.
- 6. Hager, W. and Zhang, H.-C. (2015) An Alternating Direction Approximate Newton Algorithm for Ill-Conditioned Inverse Problems with Application to Parallel MRI. Journal of the Operational Research Society of China, 3, 139-162.
- 7. Gabay, D. and Mercier, B. (1976) A Dual Algorithm for the Solution of Nonlinear Variational Problems via Finite Element Approximations. Computers & mathematics with applications, 2, 17-40.
- 8. Zhang, J.J. (2013) Solving Regularized Linear Least-Squares Problems by the Alternating Direction Method with Applications to Image Restoration. Electronic Transactions on Numerical Analysis, 40, 356-372.
- 9. Zhang, H.C. and Hager, W. (2004) A Nonmonotone Line Search Technique and Its Application to Unconstrained Optimization. Society for Industrial and Applied Mathematics, 14, 1043-1056.
- 10. Grippo, L., Lampariello, F. and Lucidi, S. (1986) A Nonmonotone Line Search Technique for Newton’s Method. SIAM Journal on Mathematical Analysis, 23, 717-716.
- 11. Eckstein, J. and Bertsekas, D. (1992) On the Douglas-Rachford Splitting Method and the Proximal Point Algorithm for Maximal Monotone Operators. Mathematical Programming, 55, 293-318.
https://doi.org/10.1007/BF01581204 - 12. Barzilai, J. and Borwein, J. (1988) Two Point Step Size Gradient Methods. IMA Journal of Numerical Analysis, 8, 141-148.
https://doi.org/10.1093/imanum/8.1.141 - 13. Raydan, M. and Svaiter, B.F. (2002) Relaxed Steepest Descent and Cauchy-Barzilai-Borwein Method. Computational Optimization and Applications, 21, 155-167.
https://doi.org/10.1023/A:1013708715892 - 14. Block, K.T., Uecker, M. and Frahm J. (2007) Undersampled Radial MRI with Multiple Coils: Iterative Image Reconstruction Using a Total Variation Constraint. Magnetic Resonance in Medicine, 57, 1086-1098.
https://doi.org/10.1002/mrm.21236 - 15. Dai, Y.H. (2002) On the Nonmonotone Line Search. Journal of Control Theory and Application, 112, 315-330.
- 16. Grippo, L., Lampariello, F. and Lucidi, S. (1989) A Truncated Newton Method with Nonmonotone Line Search for Unconstrained Optimization. Journal of Optimization Theory and Applications, 6, 401-419.
https://doi.org/10.1007/BF00940345






























