Journal of Applied Mathematics and Physics
Vol.04 No.09(2016), Article ID:71006,12 pages
10.4236/jamp.2016.49186
A Stochastic SIVS Epidemic Model Based on Birth and Death Process
Lin Zhu, Tiansi Zhang*
College of Science, University of Shanghai for Science and Technology, Shanghai, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 13, 2016; Accepted: September 26, 2016; Published: September 29, 2016
ABSTRACT
A new stochastic epidemic model, that is, a general continuous time birth and death chain model, is formulated based on a deterministic model including vaccination. We use continuous time Markov chain to construct the birth and death process. Through the Kolmogorov forward equation and the theory of moment generating function, the corresponding population expectations are studied. The theoretical result of the stochastic model and deterministic version is also given. Finally, numerical simulations are carried out to substantiate the theoretical results of random walk.
Keywords:
Epidemic Model, Vaccination, Continuous Time Markov Chain, Birth and Death Process, Stochastic Differential Equations

1. Introduction
Recently, a great interest in the analysis and prediction of consequences of public health strategies designed to control infectious disease, particularly tuberculosis and (Acquired Immune Deficiency Syndrome) AIDS [1] , has arised. The epidemic model includes vaccination and is referred to as an (Susceptible-Infected-Vaccinated-Susceptible) SIVS epidemic model, where the classes contain susceptible, infective, and vaccinated in- dividuals [1] [2] . The deterministic model was analyzed by Christopher M. Kribs-Zaleta [3] . Transmission and control of infections disease are affected by many uncertain factors, then become a stochastic process. Trend of the spread of the disease is usually only with a certain current state. That is to say, under certain conditions, each class number changes is the nature of the Mrakov process.
Birth and death process [4] is a kind of important and wide application of Markov process, the theoretical results are systematical, mature and in-depth. But various studies focused on the birth and death process itself, few people use it. Birth and death process in random environment have been researched by L. J. S. Allen and P. S. Mandal [5] [6] .
Plentful well-known stochastic epidemic models have been used to investigate questions regarding the dynamics of an epidemic [7] - [13] . There are many studies have been investigated using stochastic models [8] [14] . Our goal in this investigation is to compare the dynamics of the deterministic and the stochastic epidemic model. The stochastic models are a continuous-time Markov chain model and a stochastic dif- ferential equation model [4] [14] [15] . The stochastic differential equation model is a new formulation that is derived from the Markov chain model.
In this paper, the continuous time Markov chain model and the stochastic dif- ferential equation model based on birth and death process [4] [14] [16] are formulated based on the deterministic epidemic model. We use the cumulative generating function to express the moment equation of the numerical characteristics of random variables and Itô stochastic differential equation [4] [14] [16] of continuous time and discrete state. In addition, at the disease-free equilibrium, it is shown that the expected values of the random variables agree with the solution to the deterministic model. Finally, through extensive numerical simulations, the comparison of deterministic model and stochastic model is given.
2. Deterministic Epidemic Model
Consider a model for an (Susceptible-Infected-Susceptible)SIS disease where a vacci- nation program is in effect, which was analyzed by C. M et al. [3] . The model consists of three differential equations, one for each of the three disease states: susceptible, infective, and vaccinated, with the number in each class denoted by S(t), I(t), and V(t), respectively. The system of differential equations for the deterministic epidemic model is
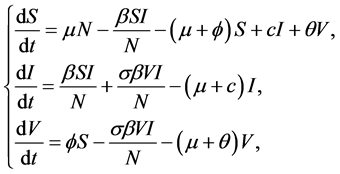 (1)
(1)
where N is the constant total population size; thus we can reduce the size of the model by letting 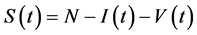 and get the new model as
and get the new model as
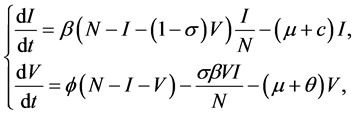 (2)
(2)
note that the parameters are all non-negative, and  is the transmission rate,
is the transmission rate, 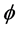 is the vaccination rate,
is the vaccination rate, 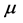 is the natural death or birth rate, c is the recovery rate,
is the natural death or birth rate, c is the recovery rate, 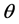 is the rate of vaccine waning. The vaccine is assumed to be useful but imperfect. Thus the vaccine efficacy denoted by
is the rate of vaccine waning. The vaccine is assumed to be useful but imperfect. Thus the vaccine efficacy denoted by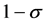 ,
, 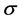 measures the efficiency of the vaccine as a multiplier to the infection rate: when
measures the efficiency of the vaccine as a multiplier to the infection rate: when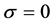 , vaccination is hundred percent effective; and when
, vaccination is hundred percent effective; and when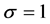 , the vaccine is totally useless.
, the vaccine is totally useless.
Although model (1) can well describe the development of the disease, in the spread and control of disease there still exist some uncertain factors such as temperature, environment of the hospital symptomtesting, etc. And the effect produced by these factors is particularly important. Based on the deterministic model (2) after dimension reduction, we take the influence of random factors on the spread of disease into considering, and establish the continuous time Markov chain (CTMC) model, namely the birth and death process.
3. The Birth and Death Process under CTMC
In this section, we construct a CTMC model under birth and death view for the epi- demic model based on the ordinary differential equation model (2). Let 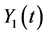 and
and 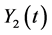 denote the discrete random variables for the number of infected and vaccinated cells at time t, the random variables
denote the discrete random variables for the number of infected and vaccinated cells at time t, the random variables 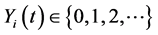 and
and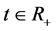 ,
,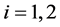 . Let the initial values be fixed,
. Let the initial values be fixed, 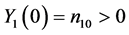 and
and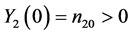 . The corresponding pro- babilities associated with the bivariate process
. The corresponding pro- babilities associated with the bivariate process 

where






where




Kolmogorov differential equation [4] . Then, we have

where
In addition, when

where
When

where 


The moment of the distribution corresponding to the bivariate process can be derived directly from the preceding forward Kolmogorov differential equation. The form of the moment generating function is

for some

By applying the product rule for differentiation, and differentiating both sides of the preceding differential Equation (10) with respect to

Take 


Differentiating both sides of the preceding differential Equation (10) with respect to

Equation (10) then gives the following differential equations for the expectation of 


From all of the above, we get

To enlarge type on the right side, it follows that

Take

then

This represents that 


For the above

is invariant. Therefore, the expectations have the same property as the variables in the deterministic model.
4. Itô Stochastic Differential Equations
Based on the CTMC model, Itô SDEs can be derived by applying the methods in [17] [19] . The possible changes of CTMC model are given in Table 1, similar to the Markov chain model.
Let 



As in the CTMC model, it is assumed that the time interval 








In addition, the variance of







where 


hence

Table 1. Possible changes in
where

for


For sufficiently small 





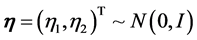



Due to that the preceding expression is an Euler-Maruyama approximation to a system of Itô stochastic differential equation [20] , that is to say, the system (28) can converge in the mean square sense to the system of Itô stochastic differential equation as follows:

where 

where 

Note 1: The form of the Itô stochastic differential equation is not unique. From the reference [18] , the form of Equation (30) can be expressed in other ways as the equivalent stochastic differential equations with the same joint probability density like

where 

with 
Note 2: Birth and death rates can be varied in forms. In the preceding formulations, we have assumed that the per capita birth and death rates of the population are positive and negative, respectively. In fact, we can take the birth and death rates from the Itô stochastic differential equation.
For example, let

where 



for redefined 


it is clear that the terms in the Wiener processes of the Itô stochastic differential equation are greater in model (35) since


5. Numerical Simulation
Numerical simulations are used to illustrate the dynamics of the deterministic model, continuous time Markov chain model and stochastic differential equation model. We simulate the birth and death process perspective of infectious disease model by ap- plying MATLAB. Throughout the paper, we choose the parameters as:








Figure 1(a) and Figure 1(b) respectively display two sample paths of the stochastic model graphed with the ordinary differential equation. It can be clearly seen from the dashed line in Figure 1 that with the change of time, infected number are gradually
Figure 1. The solution curves of deterministic model and stochastic model. In (a) and (b), the ordinary differential equation solution is attracted to the equilibrium 








increased and close to the equilibrium value. At the same time, vaccinated number are gradually reduced. One sample path for the stochastic differential equation models (30) and (35) is graphed in Figure 1(a) and Figure 1(b) with the solid line. Figure 1 shows the solution of the stochastic model fluctuates around the solution of deterministic model due to weak noise intensities which reflects that the disease will persistent.
At t = 1000, 15,000 sample paths are used to compute probability histograms for the stochastic equation models (30) and (35). The initial conditions lie in the basin of attraction for the stable endemic equilibrium for the deterministic model is 
The number of infected people is represented by the horizontal axis and vaccinated people is represented by the vertical axis. A two-dimensional random walk is given in Figure 3. It’s easy to see the path of the random walk around the equilibrium point
6. Conclusions
In this paper, two new stochastic epidemic models, namely, a continuous time Markov model and a stochastic differential epidemic model, are formulated to account for the variability inherent in the birth, death, and infection process. Our goals are to provide the solution of the stochastic model and CTMC model fluctuates around the endemic disease equilibrium

Figure 2. Probability histograms for infected number and vaccinated number distribution for taken 1000 sample path. The parameter values are







Figure 3. Random walk picture of infected number and vaccinated number in Markov model. Parameter values are







around the equilbrium point.
The continuous time Markov chain model is preferred over the stochastic differential equation model because the continuous time Markov chain model preserves the discrete population values. We also derived the formula for the fluctuation of the solution around the endemic equilibrium and obtained the ergodicity of the stochastic model. Computer simulations are presented to verify our theoretical results. Based on the parameter value, simulations of the CTMC model show for a population size N = 500 and depending on the initial values, introduction of a small number of infective individuals into a population can have similar long term outcomes in the stochastic model. We found that weak noise intensities affect long term behavior of each state slightly. These results regarding population size and choice of deterministic versus stochastic model apply to the pertussis model but may hold for more general epidemic models when the population is homogeneously mixed.
Acknowledgements
We are grateful to the editor and referees for their valuable comments that greatly improved the presentation of this paper.
Cite this paper
Zhu, L. and Zhang, T.S. (2016) A Stochastic SIVS Epidemic Model Based on Birth and Death Process. Journal of Applied Mathematics and Physics, 4, 1837- 1848. http://dx.doi.org/10.4236/jamp.2016.49186
References
- 1. Rao, P.R.S. and Kumar, M.N. (2015) A Dynamic Model for Infectious Diseases: The Role of Vaccination and Treatment. Chaos, 75, 34-49.
http://dx.doi.org/10.1016/j.chaos.2015.02.004 - 2. Zhou, Y.L. and Wang, H.Q. (2010) Analysis Of global Stability for an Epidemic Model with Quarantine and Vaccination. University of Shanghai for Science and Technology, 32, 249-252.
- 3. Kribs-Zaleta, C.M. and Velasco-Hernandez, J.X. (2000) A Simple Vaccination Model with Multiple Endemic States. Mathematical Biosciences, 164, 183-201.
http://dx.doi.org/10.1016/S0025-5564(00)00003-1 - 4. Allen, L.J.S. (2010) An Introduction to Stochastic Processes with Applications to Biology. 2nd Edition, Chapman and Hall/CRC Press, Boca Raton.
- 5. Allen, L.J.S. (2006) Stochastic Epidemic Models with a Backward Bifurcation. Mathermactical Biosciences and Engineering, 3, 445-458.
http://dx.doi.org/10.3934/mbe.2006.3.445 - 6. Mandal, P.S., Allen, L.J.S. and Banerjee, M. (2014) Stochastic Modeling of Phytoplankton Allelopathy. Applied Mathematical Modelling, 38, 1583-1596.
http://dx.doi.org/10.1016/j.apm.2013.08.031 - 7. Zhang, Y.H., Xu, C.Q. and Yuan, S.L. (2015) Stochastic SIS Epidemic Model with Contract Rate Influence by Noise. University of Shanghai for Science and Technology, 37, 511-516.
- 8. Kirupaharan, N. and Allen, L.J.S. (2004) Coexistence of Multiple Pathogen Strains in Stochastic Epidemic Models with Density-Dependent Mortality. Bulletin of Mathematical Biology, 66, 841-864.
http://dx.doi.org/10.1016/j.bulm.2003.11.007 - 9. Gray, A., Greenhalgh, D., Hu, l., Mao, X. and Pan, J. (2011) A Stochastic Differential Equation Sis Epidemic Model. SIAM: SIAM Journal on Applied Mathematics, 71, 876-902.
http://dx.doi.org/10.1137/10081856X - 10. Henson, S.M., King, A.A., Costantino, R.F., Cushing, J.M., Dennis, B. and Desharnais, R.A. (2003) Explaining and Predicting Patterns in Stochastic Population Systems. Proceedings of the Royal Society of London B, 270, 1549-1553.
- 11. Isham, V. (1991) Assessing the Variability of Stochastic Epidemics. Mathematical Biosciences, 107, 209-224.
http://dx.doi.org/10.1016/0025-5564(91)90005-4 - 12. Van Kampen, N.G. (1976) Stochastic Differential Equations. Physics Reports (Section C of Physics Letters), 24, 171-228.
http://dx.doi.org/10.1016/0370-1573(76)90029-6 - 13. Nasell, I. (1999) On the Quasi-Stationary Distribution of the Stochastic Logistic Epidemic. Mathematical Biosciences, 156, 21-40.
http://dx.doi.org/10.1016/S0025-5564(98)10059-7 - 14. Allen, L.J.S. (1945) An Introduction to Stochastic Epidemic Models. Mathematical Epidemiology.
http://link.springer.com/chapter/10.1007%2F978-3-540-78911-6_3 - 15. Kurtz, T.G. (1971) Limit Theorems for Sequences of Jump Markov Process Approximating Ordinary Differential Processes. Journal of Applied Probability, 8, 344-356.
http://dx.doi.org/10.1017/S002190020003535X - 16. Allen, E.J., Allen, L.J.S., Arciniega, A. and Greenwood, P.E. (2008) Construction of Equivalent Stochastic Differential Equation Models. Stochastic Analysis and Applications, 26, 274-297. http://dx.doi.org/10.1080/07362990701857129
- 17. Lloyd, A.L. (2004) Estimating Variability in Models for Recurrent Epidemics: Assessing the Use of Moment Closure Techniques. Theoretical Population Biology, 65, 49-65.
http://dx.doi.org/10.1016/j.tpb.2003.07.002 - 18. Ekanayake, A.J. and Allen, L.J.S. (2010) Comparison of Markov Chain and Stochastic Differential Equation Population Models Under Higher-Order Moment Closure Approximations. Stochastic Analysis and Applications, 28, 907-927.
http://dx.doi.org/10.1080/07362990903415882 - 19. Allen, E. (2007) Modeling with Itô Stochastic Differential Equations. Springer, Dordrecht.
- 20. Milosevic, M. (2016) The Euler-Maruyama Approximation of Solution to Stochastic Differential Equations with Piecewise Constant Arguments. Journal of Computational and Applied Mathematics, 298, 1-12.
http://dx.doi.org/10.1016/j.cam.2015.11.019







