Received 9 May 2016; accepted 13 June 2016; published 16 June 2016

ABSTRACT

In this paper, we build the Linear Programming (LP) model, factor analysis model and return on investment model to measure the investment amount and which year to invest of each selected schools. We firstly analyze the indicators from attached files, and select effective indexes to choose schools donated. Then we select 17 indexes out after preprocessing all the indices. Secondly, we extract 1064 schools by MATLAB which is the Potential Candidate Schools from the table of attached files; we extract 10 common factors of these schools by factor analysis. After calculation, we rank the universities and select the top 100. We calculate the Return on Investment (ROI) based on these 17 indexes. Thirdly, we figure out the investment amount by conducting LP model through MATLAB. According to the property of schools, we calculate the annual limit investment and the mount of investment of each school. Fourthly, we determine which year to invest by ROI model which is operated by LINGO. In order to achieve optimal investment strategy and not duplication of investment, for five years, starting July 2016, we assume that the time duration that the organization’s money should be provided is one year, and the school return to the Good grant Foundation only one year. Then we can get the investment amount per school, the return on that investment, and which years to invest. Fifthly, by changing parameter, the sensitivity analysis is conducted for our models. The result indicates that our models are feasible and robust. Finally, we evaluate our models, and point out the strengths and weakness. Through previous analysis, we can find that our models can be applied to many fields, which have a relatively high generalization.

Keywords:

Investment, Factors Model, LP Model, ROI Model

1. Introduction

1.1. Background

Education is the foundation of country building; it has become the key of countries to enhance their comprehensive strength and competitiveness by vigorously developing higher education. The cost of running a university is very large, and the cost of the former education is higher than the university funds. But recently this proportion has declined year by year. The shortage of funding for higher education has become a bottleneck restricting the universities’ further development. The problem of relying solely on government funding has become increasingly serious.

Therefore, if colleges and universities want to achieve better development, on the one hand they actively seek governments’ funding. On the other hand they must raise money from society initiatively. What’s more, they should use funds scientifically and rationally.

Charity is the nuclear spiritual pillar in one country’s cultural environment, while donating became the part of people’s daily life. Many rich and powerful people also regard charities as their lifelong responsibilities. Due to the cultural atmosphere of whole people-charitable, social donations become the main driving force of development of education in the United States.

Good Foundation Inc. is a small private Canadian foundation, started in 1974 by the late Milton and Verna Good. It distributes funds to charitable organizations in the communities of which family members are a part [1] . It helps improve educational performance of undergraduates attending colleges and universities in the United States.

To do this, the foundation intends to donate a total of $100,000,000 (US 100 million) to an appropriate group of schools per year, for five years, starting July 2016. In doing so, they do not want to duplicate the investments and focus of other large grant organizations such as the Gates Foundation and Lumina Foundation.

1.2. Our Work

Firstly, we should determine how many schools we would donate. In order to decide, we selected the best indexes. After selection, we may boil down the tasks to the following questions:

1) Select indexes to choose schools donated.

2) Determine an optimal investment strategy that identifies the schools.

3) The investment we donate to each school.

4) The return we will acquire by investing these schools.

2. Assumptions and Justification

1) If Good grant Foundation has selected schools that it will invest, then the time duration that the organization’s money should be provided is one year. And the school only return to the Good grant Foundation one year.

2) The funds which School return to the Good grant Foundation, the Good grant Foundation deposit the funds in bank, and the bank’s interest rates remain stable.

3) Assume that, in the t year, after we have the year’s funds (a) to be invested in schools, there is a surplus of funds (b), then the remaining funds (b) are deposited in the bank.

3. Date Analysis

3.1. The Evaluation Principles of Investment Efficiency

1) Subject to separate principles. That is carry out the subject to evaluation and the main concern. In general, the main investors or operators are the main subject. In this paper, our team want to develop a model to determine an optimal investment strategy that identifies the schools, the investment amount per school. The return on that investment, and the time duration that the organization’s money should be provided to have the highest positive effect [2] . So we choose to investor, that is Good grant Foundation as the main study subject of our thesis.

2) Evaluation Content and University functions corresponding principles. Content evaluation should be based on the “production (the output of higher education)” as the core, which is the basis for the establishment of the object being evaluation index system. Products are effective, but also to that produced sell out, that the product must “marketable”, the result of evaluation of the content must be structured to withstand market test. Therefore, when establishing the index system and evaluation of the content, it must be recognized by the market as a precondition to our evaluation of school effectiveness.

3) “Representation” principle of indicators. With the evaluation of the content, you can create content and index system to adapt. However, there are many indicators reflect the content, we can not all be used as an evaluation index. Given the relative benefit indicator is based on the principle crawl main contradiction, we only choose the education benefit relatively large index weighting factor―Representative characteristics, also has a dominant feature. So this paper, we select only representative indicators of income.

4) Normalization principle. In selecting the evaluation index system, the type of factors different from each other, can not be quantified comparison. For example, to compare cultivate a talent and made a scientific research, it is difficult to determine the pros and cons, but we may also have to face the quality problem. In this paper, we selected indicators and factor analysis, the selected indicators belonging to quantifiable indicators, and the factors are same types.

3.2. Index Selection

1) Index analysis

a) Unable to get a specific address of schools, the schools does not provide data privacy and the schools has been closed do not participate in the subsequent analyzes.

b) In terms of SAT, we choose one index in its representative, such as Average SAT equivalent score of students admitted, to carry out our further research.

c) In terms of PCIP, the data of Percentage of degrees awarded in all aspects is available, then we sum them up, as you can earn a degree student ratio

d) Select the schools that received funding from other organizations by the two indexes: Percentage of undergraduates who receive a Pell Grant and Percent of all federal undergraduate students receiving a federal student loan.

e) We summed up the student retention rate at four-year institutions by the two indexes: First-time, full-time student retention rate at four-year institutions and First-time, part-time student retention rate at four-year institutions.

f) We summed up the student retention rate at less-than-four-year institutions by the two indexes: First-time, full-time student retention rate at less-than-four-year institutions and First-time, part-time student retention rate at less-than-four-year institutions.

g) We summed up the delay graduation rate at less-than-four-year institutions by the two indexes: 150% completion rate for four-year institutions, pooled in two-year rolling averages suppressed for small n size and 200% completion rate for less-than-four-year institutions, pooled in two-year rolling averages and suppressed for small.

h) We summed up the delay graduation rate at four-year institutions by the two indexes: 150% completion rate for four-year institutions, pooled in two-year rolling averages and suppressed for small n size and 200% completion rate for four-year institutions, pooled in two-year rolling averages and suppressed for small n size.

j) In terms of which we can not operate on, we maintain its original state.

After carrying out the above process, we selected 17 index (Table 1).

2) Through factor analysis to choose the school

First, we extract 1064 schools by MATLAB from the table of Most Recent Cohorts Data, which is the Potential Candidate Schools. Second, we analyze the factors of the 1064 schools.

a) The selected indicators set to x, and we enroll the selected indicators to factor analysis in the default condition. From the output, we can obtained four common factors, which can reflect 65% of the information, but x5, x6, x10 information can not be fully reflected.

b) We want to choose schools, should choose the school as much as possible to express benefits and cost information. So we set standard is 90%, to explain 90% of variable information. From the output table, we need to extract 10 common factors, extracting 10 common factors and rotation adjustments, get Rotated Component Matrix.

c) We can get factor model from the Rotated Component Matrix:

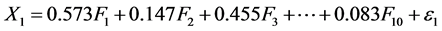(1)

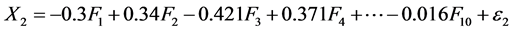(2)

∙∙∙

And get KMO is 0.752, so suitable for factor analysis. Common for all of the variables can get reactions (Table 2).

d) The “% of Variance” as the weight, which from the Extraction Sums of Squared Loadings. First, we count the scores (z) of all schools, we are based on the results of the output of the SPSS software, in the “Variance Explained Total” table, according to the “% of Variance”, we can get the mathematical formula: The scores (z) = 0.18702*FAC1_1 (the first factor) + 0.12450*FAC2_1 + 0.11387*FAC3_1 + 0.09866*FAC4_1 + 0.08038* FAC5_1 + 0.06665*FAC6_1 + 0.06357*FAC7_1 + 0.06111*FAC8_1 + 0.06095*FAC9_1 + 0.05922* FAC10_1. Second, we descending all the scores, so all schools are ranked. Last, we choose the top 100 of the schools.

We select the top 100 schools sorted by scores of models above this passage. The following table is partly data of whole date (Table 3).

e) Through factor analysis, we analysis the variables each factor represents and the actual meaning, then classify 17 indexes (Table 4).

Through the classification of the 17 indexes, we select x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃, x₁₆, x₁₇. Among them, we define F₁, F₈ and F₉ on behalf of the school’s income, F₂, F₄ on behalf of the school cost, because we will be variable points to ten, using only to income and cost, so other classification represents significant need not defined. We depend on the two kind of types to calculate ROI. World Bank senior education economist Pless Saha Luo pointed out, that “the rate of return on investment in education” and the rate of return on investment is very similar to other meanings, “Rate of return” is “at different points in time to table a summary of the costs and benefits, with the rate of return on earnings (percentage)” [3] .

4. Models

4.1. Model One

In this model, we need determine the investment of each school, to get the maximum return on investment. To solve this question, According to the schools’ assets to determine the coefficient of investment (m), we give it a value of 40, so the quantity of invest limit can be calculated. We define β_i as ROI. It can be calculated by same index mentioned above, such as aid, earnings and cost. We define that Maximum return on investment is F.

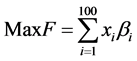
The meaning of each symbol in Table 5.

4.2. Model Two

In the selected 100 schools, we need to determine which schools and years to invest, in order to achieve optimal investment and not duplication of investment, for five years, starting July 2016. We define that Maximum income on investment is G.

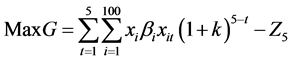
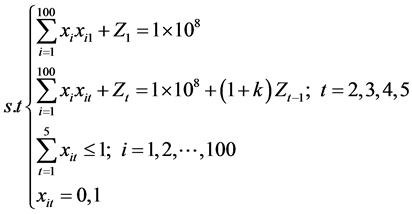
The meaning of each symbol in Table 6.

5. Model Solution

1) We solve the model one by MATLAB to get the cost, income, ROI and investment of each school, the following table is partly data of the whole date (Table 7).

2) We solve the model two by LINGO to get the investment of the 100 schools and decide which year we invest. The following table is partly data of the whole date (Table 8).

6. Sensitivity Analysis

In this section, we conduct sensitivity analysis for our model. We select x₇, x₈, x₉, x₁₀, x₁₁, x₁₂, x₁₃, x₁₆, x₁₇, these indexes include income indexes and cost indexes, we depend on the two kind of types to calculate ROI. Specifically, we test the sensitivity of parameter ROI, which we define in calculating investment amount. Tables 9-11 and Figure 1 show the results when its value is changed. We get ROI2 by delete one index, then calculate investment amount. Second, we get ROI3 by delete the other index, then calculate investment amount. Third, the same to get ROI4 by delete the other index.

As we can see, with the change of ROI, the change of investment is slightly, so that our model is optimal and feasible.

7. Strengths and Weakness

7.1. Strengths

1) In model one, the model is simple and easy to understand, and we define the return-on-investment degree, making us to carry out a quantitative analysis of return-on-investment.

2) In model one and model two, we process the data and make a variety of charts, simple and intuitional.

3) In model two, we take the variable of Z_t into consideration so that the model is more realistic.

7.2. Weakness

1) In model one, the selection of the variable of m is subjectivity.

2) In model two, we assume that the time duration that the organization’s money should be provided is one year.

Cite this paper

Jun’e Liu,Lei Chai,Zina Xu, (2016) The Models of Investing Schools. Journal of Applied Mathematics and Physics,04,1090-1098. doi: 10.4236/jamp.2016.46113

References