Journal of Applied Mathematics and Physics
Vol.04 No.05(2016), Article ID:66914,9 pages
10.4236/jamp.2016.45102
Numerical Simulation for Nonlinear Water Waves Propagating along the Free Surface
Rabab Fadhel Al-Bar
Department of Mathematics, Faculty of Science, Umm Al-Qura University, Makkah, KSA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 April 2016; accepted 27 May 2016; published 30 May 2016
ABSTRACT
The main aim of this work is to introduce the analytical approximate solutions of the water wave problem for a fluid layer of finite depth in the presence of gravity. To achieve this aim, we begun with the derivation of the Korteweg-de Vries equations for solitons by using the method of multiple scale expansion. The proposed problem describes the behavior of the system for free surface between air and water in a nonlinear approach. To solve this problem, we use the well-known analytical method, namely, variational iteration method (VIM). The proposed method is based on the use of Lagrange multipliers for identification of optimal value of a parameter in a functional. The proposed method provides a sequence of functions which may converge to the exact solution of the proposed problem. Finally, we observe that the elevation of the water waves is in form of traveling solitary waves.
Keywords:
Variational Iteration Method, Nonlinear Water Waves, Multiple Scale, Korteweg-de Vries Equations, Two Solitons Solution

1. Introduction
We are concerned with a two-dimensional, irrotational flow of an incompressible ideal fluid with a free surface under the gravitational field. The domain occupied by the fluid is bounded from below by a solid bottom. The upper surface is a free boundary, so we take the influence of the gravitational field into account on the free surface. Our main interest is motion of the free surface, which is called a gravity wave.
The Korteweg-de Vries equation (KdV) was originally derived by Korteweg and de Vries from the model surface waves in a canal. The key to a soliton’s behavior is a robust balance between the effects of dispersion and nonlinearity. When one grafts these two effects onto the wave equation for shallow water waves, then at leading order in the strengths of the dispersion and nonlinearity one gets the KdV for solitons [1] .
The Korteweg-de Vries equation was obtained by Benjamin [1] , for example, assuming that the waves were weakly nonlinear and weakly dispersive. In other words, the wave amplitude is much smaller than, for example, the upper layer thickness, and the water depth is much smaller than the typical wavelength. Solitons are among the most interesting structures in nature. Being configurations of continuous fields, they retain their localized shape even after interactions and collisions. Observed originally long ago as stable moving humps in shallow water channels, they have been established since then in various physical systems including optical wave guides, crystal lattices, Josephson junctions, plasmas and spiral galaxies [2] . Long lasting efforts to theoretically describe their intriguing properties have culminated in the development of the inverse scattering technique [3] which is among the most powerful methods to obtain exact solutions of nonlinear partial differential equations. Particularly popular examples for solitons in hydrodynamic systems are the solutions of KdV:
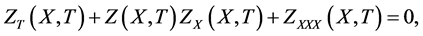 (1)
(1)
where X stands for a space coordinate, T denotes time, and Z represents the surface elevation of a liquid in a shallow duct. This equation can be derived perturbatively from the Euler equation for the motion of an incompressible and inviscid fluid [4] . The one-soliton solution of Equation (1) is given by:
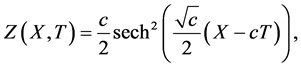 (2)
(2)
which describes a hump of invariable shape moving to the right with velocity c for all values of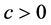 . The amplitude of the hump is given by c/2.
. The amplitude of the hump is given by c/2.
Concerning the Korteweg-de Vries approximation for water waves, we refer to Craig [5] , and Craig, et al. [6] for the approximation of the Hamiltonian. We remark that the KdV is a model of water waves in the long wave regime. The dynamics of the free surface is approximately translation of two waves without change of the shape, one moving to the right and the other to the left, for a short time interval. The dynamics of each wave is very slow so that it is invisible for the short time interval. Craig [5] gave the justification in the framework of Sobolev spaces. Schneider and Wayne gave the justification without assuming the one directional motion of the wave and extended it to the capillary-gravity waves. They showed that the interactions between two waves were negligible so that the solution of the full water wave problem was approximated by a sum of the solutions, which were appropriately scaled, of the decoupled KdVs for the long time interval. However, they treated the problem in unscaled variables, whereas Craig treated it in the scaled variables called Boussinesq ones. The nonlinear surface water waves in perturbed problem is discussed by [7] in the presence of the effect of surface tension. Based on the method of multiple scale expansion for a small amplitude, they derived two Korteweg-de Vries equations and discussed the two-soliton solution for Korteweg-de Vries equations by using analytical methods.
Many different methods have recently introduced to solve nonlinear problems such as, VIM [8] , Adomian decomposition method [9] , and homotopy perturbation method [10] . The VIM is strongly and simply capable for solving a large class of linear or nonlinear differential equations without the tangible restriction of sensitivity to the degree of the nonlinear term and also it reduces the size of calculations besides, its interactions are direct and straightforward [11] . The main aim in this work is to effectively derive the Korteweg-de Vries equations and employ VIM to establish approximate solutions of waves propagating along the interface between air-water.
The structure of the paper is organized as follows. In Section 2, we collect the basic equations and boundary conditions. In Section 3, the analysis of the VIM is introduced. In Section 4, we implement VIM to investigate the two-soliton solutions for Korteweg-de Vries equations. Finally, Section 5 contains some conclusions.
2. The Physical Problem and Basic Equations
We consider the unsteady two-dimensional flow of inviscid, incompressible fluid in a constant gravitational field. The space coordinates are (x, y) and the gravitational acceleration g is in the negative y direction. Let h be the undisturbed depth of the fluid. The bottom of the fluid is assumed to have no topography at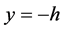 .
.
This problem describes the interface dynamics, between air and water waves, under the gravity g (see Figure 1).
The equation for the surface of water is 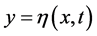 where
where 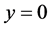 represents the equilibrium situation. We assume that the motion is irrotational within the wave. Therefore, we can describe the wave inside the water by a velocity potential
represents the equilibrium situation. We assume that the motion is irrotational within the wave. Therefore, we can describe the wave inside the water by a velocity potential 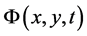 whose gradient is the velocity field:
whose gradient is the velocity field:
Figure 1. The set-up of the shallow water wave problem.
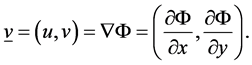 (3)
(3)
The divergence-free condition on the velocity field implies that the velocity potential 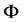 satisfies the Laplace’s equation:
satisfies the Laplace’s equation:
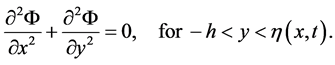 (4)
(4)
On a solid fixed boundary, the normal velocity of the fluid must vanish:
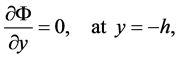 (5)
(5)
which dictates that there is no flow perpendicular to the bottom.
The boundary conditions at the free surface  are given by:
are given by:
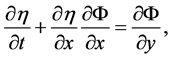 (6)
(6)
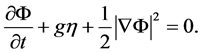 (7)
(7)
Now we try to find the approximate solutions by using VIM of following Korteweg-de Vries equations (which are derived in details in [12] ):


3. Analysis of the Variational Iteration Method
To illustrate the analysis of VIM [13] , we limit ourselves to consider the following nonlinear differential equation in the type:

with specified initial conditions, where L and R are linear bounded operators, and 

It is obvious that the successive approximations 











In what follows, we will apply VIM to Korteweg-de Vries Equations (8)-(9) to illustrate the strength of the method and to obtain the approximate solutions for this nonlinear problem.
Now, to illustrate how to find the value of the Lagrange multiplier

Making the above correction functional stationary, and noticing that
where 


The first equation in (13) is called Lagrange-Euler equation and the second equation in (13) is called natural boundary condition, the Lagrange multiplier, therefore, can be readily identified,
Now, the following variational iteration formula can be obtained:

We start with an initial approximation, and by using the above iteration formula (14), we can obtain directly the other components of the solution.
4. Numerical Application
In this section, we will implement VIM to Korteweg-de Vries Equations (8)-(9), with the initial conditions:
To solve Equations (8)-(9) by means of VIM, we construct the correction functionals which read:


Making the above correction functional stationary, and noticing that
where 




The Lagrange multipliers

Now, the following variational iteration formula can be obtained:


We start with an initial approximations




Returning to dimensional variables, we get:




In the same manner, we can obtain other components of the solution. In order to verify numerically whether the proposed methodology lead to higher accuracy, we can evaluate the numerical solutions using 

From the above solution process, we can see clearly that the approximate solutions converge to its exact solution relatively slowly due to the approximate identification of the multiplier. It should be specially pointed out that the more accurate the identification of the multiplier, faster the approximations converge to its exact solutions.
After returning to dimensional variables and substitution from (27) into (3) we get the elevation of the water surface, the horizontal velocity, the vertical velocity and the phase diagrams of the velocity, which describes the physical situation of the system, where:





The water wave gradually splits into two solitary waves with increasing 

5. Conclusions and Discussion
In this study, we present model equations for surface water waves by using a new method of multiple scale technique. Multiple scale technique is used to estimate the Korteweg-de Vries equations for the nonlinear theory, describing the behaviour of the perturbed system. We observed that the method of multiple scale was one
Figure 2. The water wave at 

Figure 3. The water wave at 

Figure 4. The water wave at 

Figure 5. The water wave at 

of the modern methods which we used to obtain the Korteweg-de Vries equations because it was relatively short in mathematical calculation, more effective and more enlightening. While the Hamiltonian expansions and the Dirichlet-Neumann operator expansions are complex in mathematical calculation and relatively long method
Figure 6. The horizontal velocity (left). The vertical velocity (right).
as compared with the method of multiple scale.
The diagrams are drawn to illustrate the elevation of the water waves that show a solitary character. We observed that the elevation of the water waves is in form of traveling solitary waves, which increases in amplitude as the wave number increases.
Finally, the horizontal and vertical velocities of the velocity components have nonlinear characters, which describes the physical situation of the system for free surface between air and water.
The presented examples show that the results of the proposed method VIM are in excellent agreement with the exact solution. An interesting point about VIM is that only few iterations or, even in some special cases, one iteration, lead to exact solutions or solutions with high accuracy. The main merits of VIM are:
1) VIM can overcome the difficulties arising in calculation of Adomian’s polynomials in Adomain decomposition method.
2) VIM does not require small parameters which are needed in perturbation method.
3) No linearization is needed; the method is very promising for solving wide application in nonlinear differential equations.
In our work, we used the Mathematica Package.
Acknowledgements
The author thanks the Editor and the referee for their comments.
Cite this paper
Rabab Fadhel Al-Bar, (2016) Numerical Simulation for Nonlinear Water Waves Propagating along the Free Surface. Journal of Applied Mathematics and Physics,04,930-938. doi: 10.4236/jamp.2016.45102
References
- 1. Benjamin, T.B. (1966) Internal Waves of Finite Amplitude and Permanent Form. Journal of Fluid Mechanics, 25, 241-253.
http://dx.doi.org/10.1017/S0022112066001630 - 2. Drazin, P.G. and Johnson, R.S. (1996) Solitons: An introduction. Cambridge University Press, Cambridge, England.
- 3. Gardner, C.S., Greene, J.M., Kruskal, M.D. and Miura, R.M. (1976) Method for Solving the Korteweg-de Vries Equation. Physical Review Letters, 19, 1059-1084.
- 4. Whitham, G.B. (1974) Linear and Nonlinear Waves. Wiley, New York.
- 5. Craig, W. (1985) An Existence Theory for Water Waves and the Boussinesq and Korteweg-de Vries Scaling Limits. Communications in Partial Differential Equations, 10, 787-800.
http://dx.doi.org/10.1080/03605308508820396 - 6. Craig, W., Guyenne, P., Nicholls, D.P. and Sulem, C. (2005) Hamiltonian Long Wave Expansions for Water Waves over a Rough Bottom. Proceedings of The Royal Society of London A: Mathematical, Physical and Engineering Sciences, 461, 839-845.
http://dx.doi.org/10.1098/rspa.2004.1367 - 7. Abourabia, A.M., Mahmoud, M.A. and Khedr, G.M. (2008) Korteweg-de Vries Type Equations for Waves Propagating along the Interface between Air-Water. Canadian Journal of Physics, 86, 1427-1435.
- 8. Abassy, T.A., El-Tawil, M.A. and El Zoheiry, H. (2007) Solving Nonlinear Partial Differential Equations Using the Modified Variational Iteration Padé Technique. Journal of Computational and Applied Mathematics, 207, 73-81.
http://dx.doi.org/10.1016/j.cam.2006.07.024 - 9. Khader, M.M. (2014) A New Formula for Adomian Polynomials and the Analysis of Its Truncated Series Solution for the Fractional Non-Differentiable IVPs. ANZIAM Journal, 55, 69-80.
http://dx.doi.org/10.1017/S1446181113000321 - 10. Sweilam, N.H., Khader, M.M. and Al-Bar, R.F. (2007) Numerical Studies for a Multi-Order Fractional Differential Equation. Physics Letters A, 371, 26-33.
http://dx.doi.org/10.1016/j.physleta.2007.06.016 - 11. Liu, H. and Yan, J. (2006) A Local Discontinuous Galerkin Method for the Korteweg-de Vries Equation with Boundary Effect. Journal of Computational Physics, 215, 197-206.
http://dx.doi.org/10.1016/j.jcp.2005.10.016 - 12. Khader, M.M. and Al-Bar, R.F. (2011) Approximate Method for Studying the Waves Propagating along the Interface between Air-Water. Mathematical Problem in Engineering, 2011, Article ID: 147327.
http://dx.doi.org/10.1155/2011/147327 - 13. He, J.H. (2000) Variational Iteration Method for Autonomous Ordinary Differential Systems. Applied Mathematics and Computation, 114, 115-126.
http://dx.doi.org/10.1016/S0096-3003(99)00104-6 - 14. Elsgolts, L. (1977) Differential Equations and the Calculus of Variations. Translated from the Russian by Yankovsky, G., Mir, Moscow.














