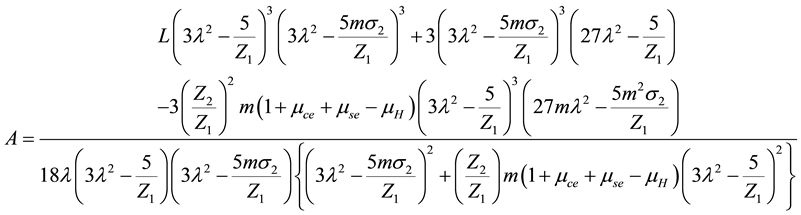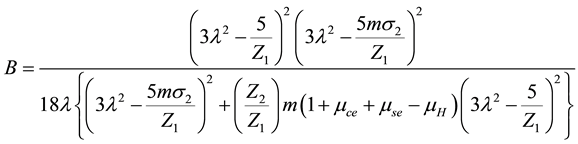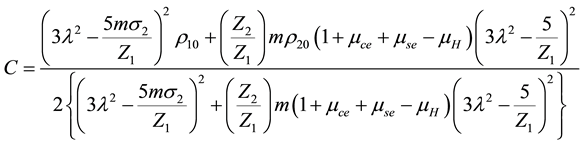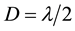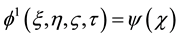Journal of Applied Mathematics and Physics
Vol.03 No.11(2015), Article ID:61397,12 pages
10.4236/jamp.2015.311171

Kadomstev-Petviashvilli-Burgers (KPB) Equation in a Five Component Cometary Plasma with Kappa Described Electrons and Ions

Manesh Michael1, Sreekala Gopinathan1, Sijo Sebastian1, Neethu T. Willington2, Anu Varghese1, Renuka Gangadharan3, Chandu Venugopal1*

1School of Pure & Applied Physics, Mahatma Gandhi University, Priyadarshini Hills, Kottayam, Kerala, India

2Department of Physics, C. M. S. College, Kottayam, India

3Kerala State Council for Science, Technology & Environment, Sasthra Bhavan, Pattom, Thiruvananthapuram, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 19 October 2015; accepted 20 November 2015; 24 November 2015

ABSTRACT

We investigate the existence of Ion-Acoustic solitary/shock waves in a five component cometary plasma consisting of positively and negatively charged oxygen ions, kappa described hydrogen ions, hot electrons and cold electrons. The KPB equation is derived for the system; its solution is plotted for different kappa values, as well as for the temperature ratios of ions. It is found that the amplitude of solitary structure increases with increasing kappa values and negatively charged oxygen ion densities. As the temperature of the positively charged oxygen ions increases, the amplitude of solitary wave also increases. We have also studied the dependence of coefficients of the KPB equation on physical parameters relevant to comet Halley.

Keywords:

Cometary Multi-Ion Plasma, Ion-Acoustic Solitary Wave, Shock Wave, KPB Equation

1. Introduction

Nonlinear wave structures arise due to the interplay of nonlinearity, dispersion and dissipation. They are one of the most beautiful and astonishing manifestations of nature. Solitons, shock waves, double-layers, etc. are some nonlinear phenomena observed in space, astrophysical and laboratory plasmas.

In the past few decades nonlinearity of ion acoustic waves, which is an important wave in a plasma, has been studied extensively. The first nonlinear analysis of the ion acoustic wave was done by Sagdeev [1] ; its first experimental observation was by Ikezi et al. [2] . The observations by Viking and Freja spacecrafts have identified solitary structure in the magnetosphere as density depressions.

When a medium has both dispersion and dissipation, the propagation characteristics of small-amplitude perturbations can be adequately described by the Korteweg-deVries-Burgers equation (KdVB) in a one-dimen- sional and by the Kadomtsev-Petviashvilli-Burgers (KPB) equation in a two-dimensional geometry. The dissipative Burger term in both the nonlinear KdVB and KPB equations arises from the kinematic viscosity of the plasma constituents [3] - [5] . When the wave breaking due to nonlinearity is balanced by the combined effect of dispersion and dissipation, a monotonic or oscillatory dispersive shock wave is generated in a plasma [6] .

Many powerful methods have been established and developed to study these nonlinear equations by using the standard reductive perturbation method, but the one-dimensional form of the expression cannot explain the complete picture of all solitary waves formed in nature. In 1970, Kadomtsev and Petviashvilli [7] proposed a multi-dimensional dispersive wave equation to study the stability of one soliton solution of the KdV equation under the influence of weak transverse perturbations. This KP equation is a partial differential equation which describes the nonlinear wave motion in more than one dimension and since then the KP equation has been used considerably in describing the nonlinear dynamics of plasmas. Thus, for example, the propagation of nonlinear ion acoustic waves and shocks were studied in dusty plasma [8] and the electron-positron-ion (e-p-i) plasma [9] - [14] . The nonlinear propagation of ion acoustic waves in a magnetised plasma has been studied using the Sagdeev potential method and computer simulation where the electrons were described by a kappa distribution [15] [16] . This was further complemented by studies on the linear and nonlinear propagation of electron acoustic waves in a two temperature electron plasma where again the hot electron component was described by a kappa distribution [17] [18] . These studies were further extended to a multi-ion, collisionless plasma composed of two distinct kappa described electrons, Maxwellian positrons and stationary negatively charged heavy ions [19] . With the realization of the growing importance of pair ion plasmas, various aspects of shocks and solitons in these plasmas were also studied [20] - [22] .

Plasmas observed in different space environments deviate significantly from the well known Maxwellian distribution due to the presence of high energy particles in the tail of the distribution. Using solar wind data Vasyliunas first predicted a non-Maxwellian distribution [23] ; this distribution, which subsequently came to be known as the “kappa distribution”, has been found in many magnetospheric and astrophysical environments.

It is well known that a cometary plasma is composed of hydrogen ions, electrons, and new born heavier ions with relative densities depending on their distances from the nucleus. Initially, the positively charged oxygen ion was considered as the main heavier ion [24] [25] . But the discovery of negatively charged oxygen ions [26] enables one to treat the plasma environment around the comet as a pair-ion plasma (O+, O−) with other ions (both lighter and heavier) constituting the other components of the plasma. As regards electrons, many cometary atmospheres have more than one component. For instance, the electron distribution in the tail of comet Giacobini- Ziner was observed to have three components: a cold component, a mid component and a hot component―the mid component was interpreted as having a sizeable contribution from the photo-electrons generated by the ionisation of cometary neutrals [27] . Also, in a study of comets with high total gas production rates, the observed double peak structure was interpreted as due to the effective degradation of soft x-rays and the consequent production of energetic photo-electrons [28] . We thus divide the cometary electrons into a primary, hot component and a secondary, colder photo-electron component.

Thus a cometary plasma is a true multi-ion plasma consisting of both lighter and heavier ions and electrons with different temperatures. We thus model our plasma as consisting of a pair-ion plasma of oxygen ions, lighter hydrogen ions and two components of electrons with different temperatures. And for reasons given above, the lighter hydrogen ions and electrons are modeled by kappa distributions.

Giotto observations of comet Halley found a very complex structure of multiple sub-shocks or interplanetary structures. However, unambiguous observations were provided by Vega-1 which found bow shock crossings for both inward and outward journeys ( [29] and references there in). And also as discussed by Coates [29] , heavy ions seriously affect shock structures due to mass loading of the solar wind and pick up ion driven instabilities. And these heavy ions can be both positively and negatively charged as discussed above. Also in a recent study, Voelzke and Izaguirre analysed 886 images of comet Halley to understand the morphological features of the tail of the comet [30] . Forty one solitary structures were clearly identified.

We therefore study ion acoustic solitary/shock structures in a plasma of the above composition. The Kadomtsev-Petviashvilli-Burgers (KPB) equation is derived using the reductive perturbation technique. For typical values observed at comet Halley, we find that the solitary wave structure transforms to a shock like structure with a decrease of spectral index kappa and negatively charged oxygen ion densities. The amplitude of the solitary wave also increases with increasing temperature of positively charged oxygen ions. We have also studied the dependence of coefficients of KPB equation on physical parameters relevant to comet Halley.

2. Basic Equations

We consider the existence of Ion-Acoustic solitary/shock waves in a five component plasma for reasons given above. The plasma consists of positively and negatively charged oxygen ions, kappa described hydrogen ions, hot electrons of solar origin and colder electrons of cometary origin. At equilibrium the charge neutrality condition can be written as,

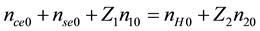
where, 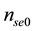represent the equilibrium densities of cometary electrons and solar electrons respectively where as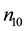, , 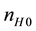are the equilibrium densities of negatively charged oxygen (O−) ions, positively charged oxygen (O+) ions and hydrogen ions respectively. Z1 and Z2 represent the charge numbers of O− and O+ ions respectively.

The kappa distribution of species ‘s’ is given by,

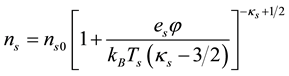(1)

In (1), s = H for hydrogen, 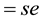for solar electrons and 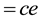for cometary photo-electrons. denotes the density (with the subscript “0” denoting the equilibrium value), 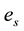the charge, 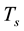the temperature and the spectral index for the species “s”. 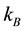is the Boltzmann’s constant and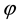, the potential.

The dynamics of heavier ions can be described by the following hydrodynamic equations:

(2)

(3)

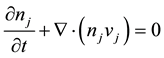
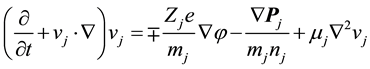
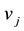
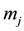
where and, respectively, denote the fluid velocity and mass of j-species of ions (j = O−, O+). In (3) the

adiabatic equation of state for ions, is where, for three dimensional

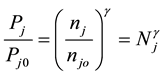
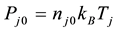
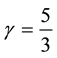
geometry of the system and is the ion kinematic viscosity.

The Poisson’s equation is given by

(4)

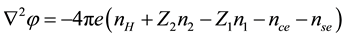
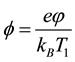
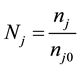
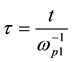
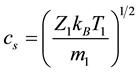
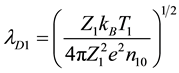
We normalize (2) to (4) using the parameters of O− ions according to, , , , where and. The variable x is normalized using.

Thus, (2) to (4) can be rewritten as,

(5)

(6)

(7)

(8)

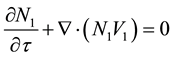
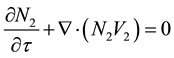
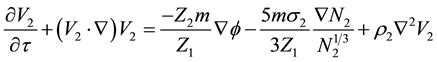
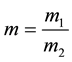
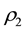
where, , and.

and now represent the normalized kinematic viscosities of the pair ions.

The normalized Poisson’s equation after substitution of (1) is,

(9)

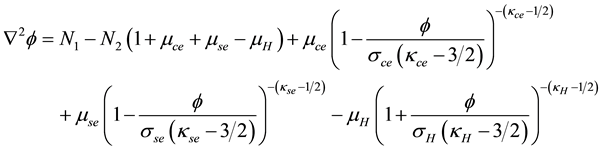
where, , , , and.

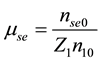
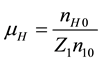
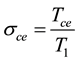
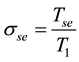
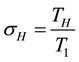
3. Derivation of Kadomstev-Petviashvilli-Burgers (KPB) Equation

We use the reductive perturbation method to derive the KPB equation from (5) to (9) by introducing the transformations [31]

, , , ,

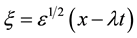
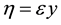
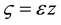
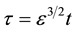
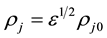
where ε is a smallness parameter and λ is the wave phase speed.

For applying the reductive perturbation technique the various parameters are expanded as,

(10)

(11)

(12)

(13)

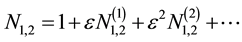
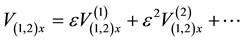
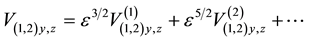
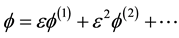
We substitute (10) to (13) in (5) to (9) and equate the coefficients of different powers of ε. From the coefficients of order we get the first order terms as,

(14)

(15)

(16)

(17)

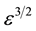
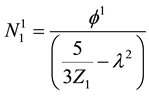
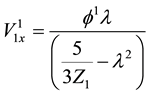
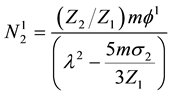
In addition, the linear dispersion relation is

(18)

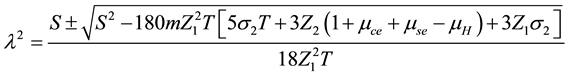
where and

Equating the coefficients of in (5) and (6), we get

(19)

(20)

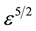
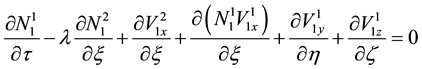
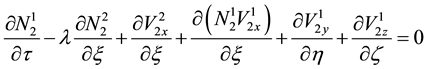
and equating the coefficient of order in (7) and (8) gives,

(21)

(22)

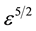
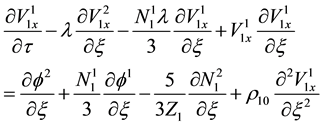
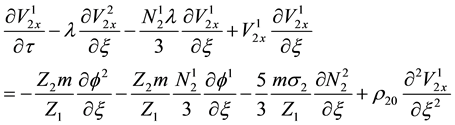
Finally, equating the coefficients of ε2 from Poisson’s Equation (9) gives,

(23)

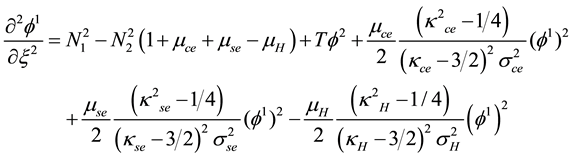
Substituting the values from (14) to (18) into (19) to (23) and eliminating the second order terms, we obtain the KPB equation as

(24)

Here the coefficients A and B represent the nonlinearity and dispersion respectively; while C and D are respectively due to the kinematic viscosities and transverse perturbations. These coefficients are given by

where L is

As a check on our results we note that they reduce to that in Dev et al. [31] when the additional ion and electron components are removed.

4. Discussion

Equation (24) is the KPB equation in a five component plasma consisting of a pair of heavier, oxygen ions, lighter hydrogen ions and two components of electrons at different temperatures. When the density of the second component of electrons is set equal to zero, (24) can be used to study the effect of a third ion component on ion acoustic shocks in a pair ion plasma. Our results can thus be considered as extensions of the results of the studies on ion-acoustic shocks in pair-ion plasmas [20] - [22] . Similarly, by an appropriate choice of masses, our studies can be made to complement the studies on ion-acoustic shock waves in e-p-i plasmas [9] - [14] [18] .

5. Solution of KPB Equation

In order to find the solution of (24) we use the transformations

and

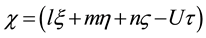
where l, m and n are the direction cosines along the x, y and z axes.

When the partial differential equation of a system is formed by the combined effect of dispersion and dissipation, the most convenient and efficient method to solve it is “the tanh method” [32] [33] . Using the tanh method, we arrive at the solution for (24), as

(25)

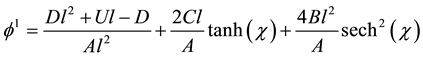
6. Results

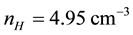
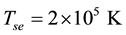
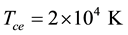
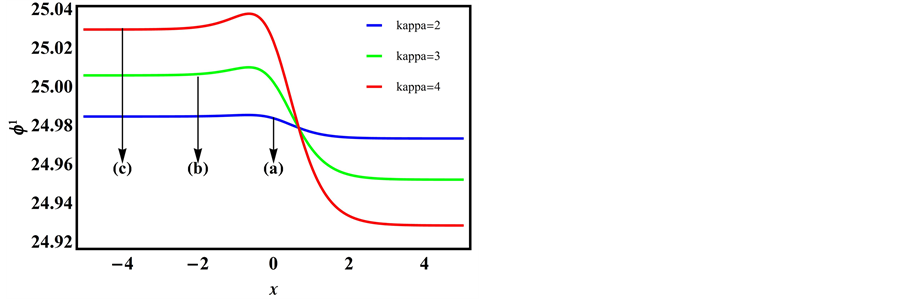
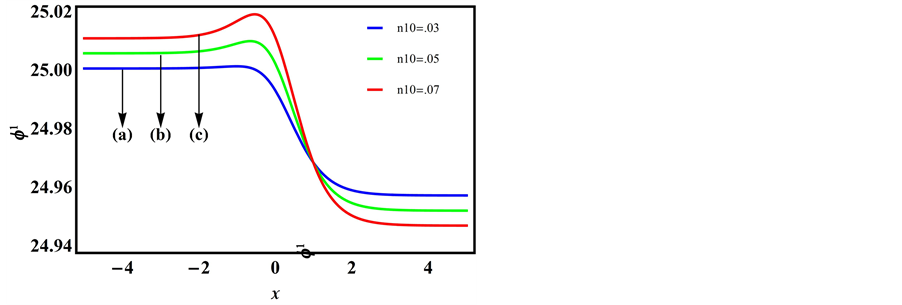
Though our Equation (24) is applicable to any plasma we are interested, in this paper, on parameters relevant to comet Halley. The observed value of the density of hydrogen ions was; their temperature was. The temperature of the solar (or hot) electrons was [34] . The temperature of the second component of the photo-electron was set at. Negatively charged oxygen ions with an energy~1eV and densities ≤ 1 cm−3 was unambiguously identified by Chaizy et al. [26] . We thus set the densities of positively charged oxygen ions at and that of negatively charged oxygen ions at [26] [34] .

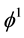
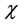
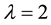
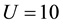
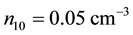
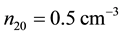
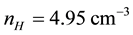
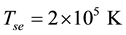
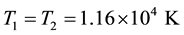
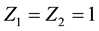
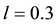
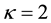
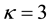
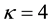
Figure 1 is a plot of the solution of the KPB equation (25) and depicts the variation of the potential versus; the parameters for the figure are, , , , , , , , ,. Curve (a) (blue colour) is for the spectral index, curve (b) (green colour) is for and curve (c) (red colour) is for. We find that as the spectral index kappa decreases the solitary wave transforms to a shock like structure. This result is in agreement with the result of Pakzad [10] who studied IA shock waves in a e-p-i plasma.

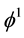
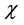
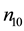
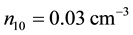
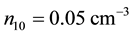
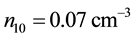
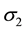
Figure 2 is again a plot of the potential versus as a function of the negative ion densities; the other parameters are the same as in Figure 1. In this case we keep the spectral index kappa as

. Curve (a) (blue colour) is for, curve (b) (green) is for and curve (c) (red) is for. We find that the solitary wave transforms into a shock like structure as the densities of negative oxygen ions decrease. Other results obtained were that the soliton amplitude decreases with decreasing and is almost independent of the positively charged oxygen ion densities.

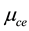
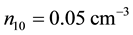
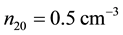
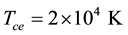
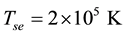
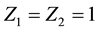
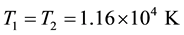
Figure 3 is a plot of the nonlinearity A versus: the parameters for the figure are, , , , , ,. Curve (a) (blue colour) is for the spectral index, curve (b) (green colour) for and curve (c) for

Figure 1. ϕ1 vs χ as a function of kappa indices.

Figure 2. ϕ1 vs χ as a function of O− ion density.

(red). We find that the nonlinearity parameters decreases with increasing.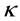

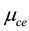
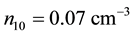
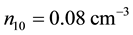
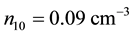
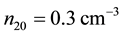
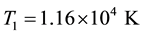
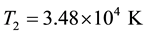
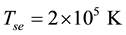
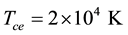
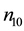
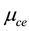
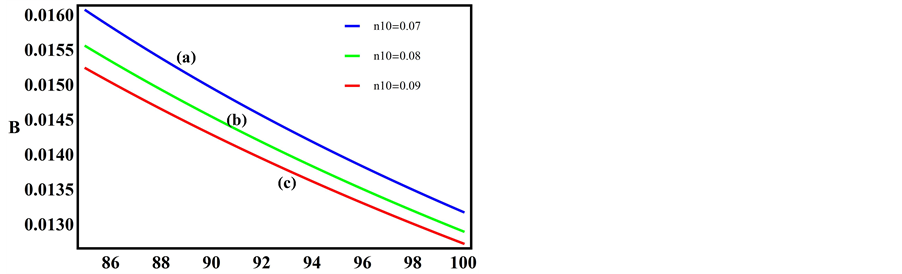
The dependence of the same parameter on negatively charged oxygen ion densities is studied next. Figure 4 thus depicts the variation of A versus for three values of the negatively charged oxygen density. Curve (a) is for (blue), curve (b) is for (green) and curve(c) is for (red). The other parameters for the figure are:, , , , , , and. We find that the nonlinearity A is very sensitive to the variation of and increases with increasing negatively charged oxygen ion densities. The variation of A with as a function of O+ density is similar; however the variation is not as sensitive.

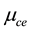
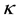
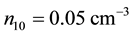
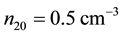
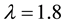
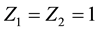
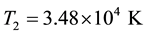
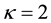
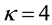
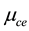
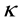
The variation of the dispersive term B is depicted next. Figure 5 is thus a plot of B versus as a function of; the other parameters are, , , ,. Curve (a) (blue) is for, curve (b) (green) is for and curve (c) is for (red). We find that the dispersive term B increases with increasing. The behaviour of the dissipation term C with as a function of is similar to the behaviour of B, and hence opposite to that of the nonlinear term A.

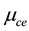
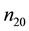
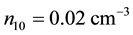
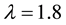
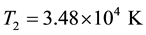
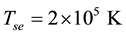
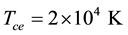
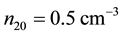
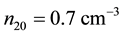
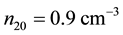
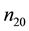
Figure 6 is also a plot of B versus as a function of; the parameters for the figure are

, , , , , , ,. Curve (a) (blue) is for, curve (b) (green) is for and curve (c) is for (red). The dispersive term B decreases with increasing.

Figure 7, is also a plot of B versus as a function of. Curve (a) is for a density curve (b) is for and curve (c) is for; the other parameters are the same as in Figure 4. We find that the dispersive term B decreases with increasing negatively charged oxygen ion densities.

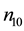
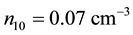
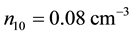
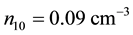
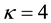
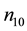
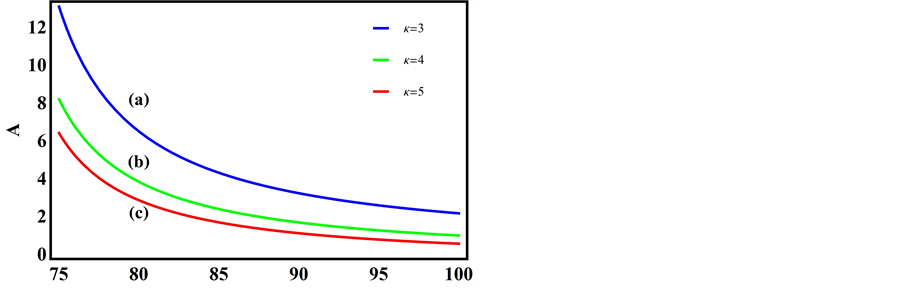
Figure 8 and Figure 9 depict the variation of dissipative coefficient C as a function of kappa indices and negatively charged oxygen ion densities respectively. The parameters for Figure 8 are the same as that of Figure 5. Curve (a) is for, curve (b) is for and curve (c) is for; we see C decreases as decreases. Finally Figure 9 depicts the variation of C with as a function of, the other parameters are same as in

μce

Figure 3. A vs μce as function of kappa indices.

μce

Figure 4. A vs μce as function of n10.

μce

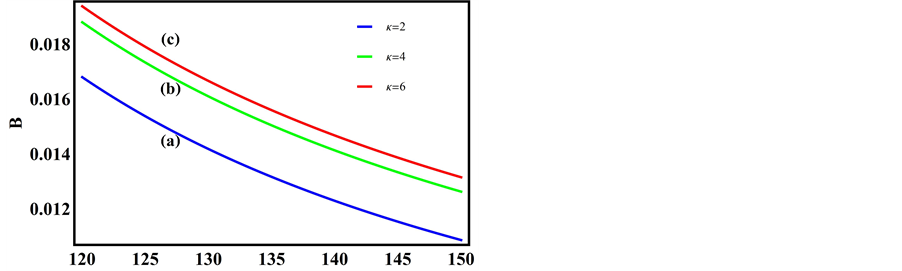
Figure 5. B vs μce as function of kappa indices.

μce

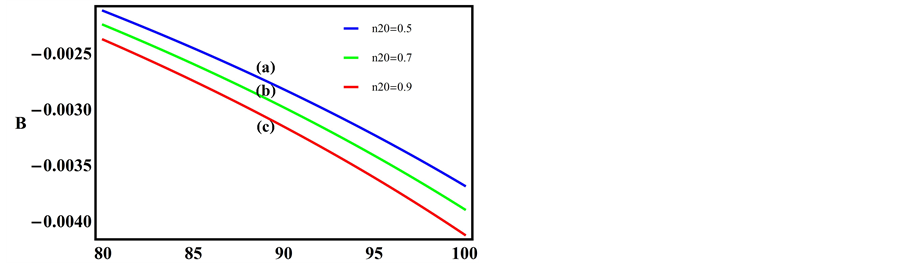
Figure 6. B vs μce as function of n20.

Figure 7. B vs μce as function of n10.

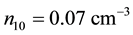
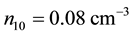
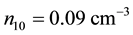
Figure 4. Curve (a) is for, curve (b) is for and curve (c) is for. We find that C decreases with increasing negatively charged oxygen ion densities. It is clear that variation of C resembles that of the dispersive coefficient B.

Thus the behaviour of the nonlinear term A is opposite to the behaviour of the dispersion term B and the dissipative term C. When the wave breaking due to nonlinearity is balanced by the combined effect of dispersion and dissipation, a monotonic or oscillatory dispersive shock wave is generated in a plasma [6] .

7. Conclusion

We have, in this paper, studied ion acoustic solitary waves/shock waves in a five component plasma of positively and negatively charged oxygen ions, lighter hydrogen ions and hot and cold electrons by deriving the KPB equation. The lighter ion and the two electron components are described by kappa distributions. The solution

μce

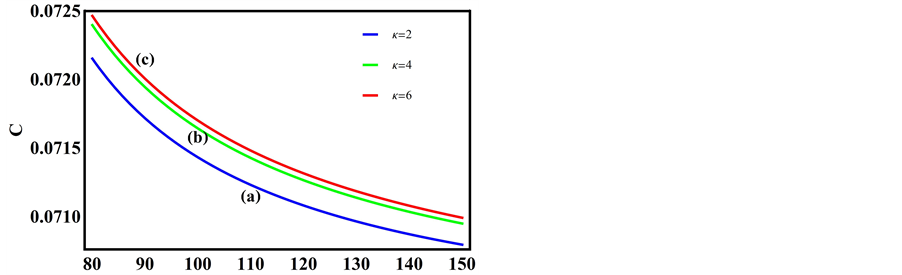
Figure 8. C vs μce as function of kappa indices.

μce

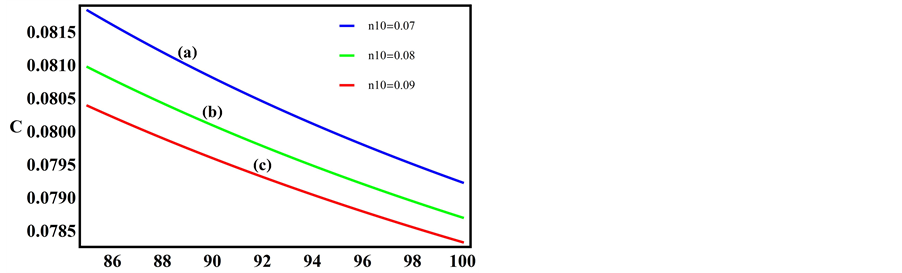
Figure 9. C vs μce as function of n10.

of the KPB equation shows that decreasing spectral indices transform the solitary wave into a shock like structure. A reduction in the solitary wave amplitude is seen with a decreasing negatively charged oxygen ion densities and positively charged oxygen ion temperatures. These results can be expected to contribute to an understanding of shocks in comets as we have two heavy ion components and heavy ions were surmised to affect shocks in cometary plasmas [29] .

Acknowledgements

We thank the referee for the very useful comments. Financial assistance from Kerala State Council for Science, Technology & Environment, Thiruvananthapuram, Kerala, India (JRFs for MM and SG) and the University Grants Commission (EF) is gratefully acknowledged.

Cite this paper

ManeshMichael,SreekalaGopinathan,SijoSebastian,Neethu T.Willington,AnuVarghese,RenukaGangadharan,ChanduVenugopal, (2015) Kadomstev-Petviashvilli-Burgers (KPB) Equation in a Five Component Cometary Plasma with Kappa Described Electrons and Ions. Journal of Applied Mathematics and Physics,03,1431-1442. doi: 10.4236/jamp.2015.311171

References

  1. 1. Sagdeev, R.Z. and Leontovich, M.A. (1966) Cooperative Phenomena and Shock Waves in Collisionless Plasmas. Reviews of Plasma Physics, 4, 23.

  2. 2. Ikezi, H., Taylor, R. and Baker, D. (1970) Formation and Interaction of Ion-Acoustic Solitions. Physical Review Letters, 25, 11.
    http://dx.doi.org/10.1103/PhysRevLett.25.11

  3. 3. Mamun, A.A. and Shukla, P.K. (2002) Cylindrical and Spherical Dust Ion-Acoustic Solitary Waves. Physics of Plasmas, 9, 1468.
    http://dx.doi.org/10.1063/1.1458030

  4. 4. Xue, J.K. (2003) Cylindrical and Spherical Dust-Ion Acoustic Shock Waves. Physics of Plasmas, 10, 4893.
    http://dx.doi.org/10.1063/1.1622954

  5. 5. Sahu, B. and Roychoudhury, R. (2007) Quantum Ion Acoustic Shock Waves in Planar and Nonplanar Geometry. Physics of Plasmas, 14, 072310.
    http://dx.doi.org/10.1063/1.2753741

  6. 6. Shukla, P.K. and Mamun, A.A. (2003) Solitons, Shocks and Vortices in Dusty Plasmas. New Journal of Physics, 5, 17.
    http://dx.doi.org/10.1088/1367-2630/5/1/317

  7. 7. Kadomstev, B.B and Petviashvilli, V.I. (1970) On the Stability of Solitary Waves in Weakly Dispersing Media. Soviet Physics Doklady, 15, 539.

  8. 8. Moslem, W.M. (2006) Dust-Ion-Acoustic Solitons and Shocks in Dusty Plasmas. Chaos, Solitons & Fractals, 28, 994-999.
    http://dx.doi.org/10.1016/j.chaos.2005.08.150

  9. 9. Masood, W., Imtiaz, N. and Siddiq, M. (2009) Ion Acoustic Shock Waves in Dissipative Electron Positron-Ion Plasmas with Weak Transverse Perturbations. Physica Scripta, 80, 015501.
    http://dx.doi.org/10.1088/0031-8949/80/01/015501

  10. 10. Pakzad, H.R. (2011) Ion Acoustic Shock Waves in Dissipative Plasma with Superthermal Electrons and Positrons. Astrophysics and Space Science, 331, 169-174.
    http://dx.doi.org/10.1007/s10509-010-0424-9

  11. 11. Pakzad, H.R. and Javidan, K. (2011) Ion Acoustic Shock Waves in Weakly Relativistic and Dissipative Plasmas with Non Thermal Electrons and Thermal Positrons. Astrophysics and Space Science, 331, 175-180.
    http://dx.doi.org/10.1007/s10509-010-0444-5

  12. 12. Chatterjee, P., Ghosh, D.K. and Sahu, B. (2012) Planar and Nonplanar Ion Acoustic Shock Waves with Nonthermal Electrons and Positrons. Astrophysics and Space Science, 339, 261-267.
    http://dx.doi.org/10.1007/s10509-012-1011-z

  13. 13. Ghosh, D.K., Chatterjee, P., Mandal, P.K. and Sahu, B. (2013) Nonplanar Ion-Acoustic Shocks in Electron-Positron-Ion Plasmas: Effect of Superthermal Electrons. Pramana, 81, 491-501.
    http://dx.doi.org/10.1007/s12043-013-0588-2

  14. 14. Hussain, S., Ur-Rehman, H. and Mahmood, S. (2014) Two Dimensional Ion Acoustic Shocks in Electron-Positron-Ion Plasmas with Warm Ions, and q-Nonextensive Distributed Electrons and Positrons. Astrophysics and Space Science, 351, 573-580.
    http://dx.doi.org/10.1007/s10509-014-1868-0

  15. 15. Sultana, S., Kourakis, I., Saini, N.S. and Hellberg, M.A. (2010) Oblique Electrostatic Excitations in a Magnetized Plasma in the Presence of Excess Superthermal Electrons. Physics of Plasmas, 17, Article ID: 032310.
    http://dx.doi.org/10.1063/1.3322895

  16. 16. Kourakis, I., Sultana, S. and Hellberg, M.A. (2012) Dynamical Characteristics of Solitary Waves, Shocks and Envelope Modes in Kappa-Distributed Non-Thermal Plasmas: An Overview. Plasma Physics and Controlled Fusion, 54, Article ID: 124001.
    http://dx.doi.org/10.1088/0741-3335/54/12/124001

  17. 17. Sultana, S., Kourakis, I. and Hellberg, M.A. (2012) Oblique Propagation of Arbitrary Amplitude Electron Acoustic Solitary Waves in Magnetized Kappa-Distributed Plasmas. Plasma Physics and Controlled Fusion, 54, Article ID: 105016.
    http://dx.doi.org/10.1088/0741-3335/54/10/105016

  18. 18. Sultana, S. and Kourakis, I. (2012) Electron-Scale Electrostatic Solitary Waves and Shocks: The Role of Superthermal Electrons. The European Physical Journal D, 66, 100.
    http://dx.doi.org/10.1140/epjd/e2012-20743-y

  19. 19. Sultana, S. and Mamun, A.A. (2014) Linear and Nonlinear Propagation of Ion-Acoustic Waves in a Multi-Ion Plasma with Positrons and Two-Temperature Superthermal Electrons. Astrophysics and Space Science, 349, 229-238.
    http://dx.doi.org/10.1007/s10509-013-1634-8

  20. 20. Masood, W., Mahmood, S. and Imtiaz, N. (2009) Electrostatic Shocks and Solitons in Pair-Ion Plasmas in a Two-Dimensional Geometry. Physics of Plasmas, 16, Article ID: 122306.
    http://dx.doi.org/10.1063/1.3272666

  21. 21. Masood, W. and Rizvi, H. (2012) Two Dimensional Nonplanar Evolution of Electrostatic Shock Waves in Pair-Ion Plasmas. Physics of Plasmas, 19, Article ID: 012119.
    http://dx.doi.org/10.1063/1.3677779

  22. 22. Samanta, U.K., Chatterjee, P. and Mej, M. (2013) Soliton and Shocks in Pair Ion Plasma in Presence of Superthermal Electron. Astrophysics and Space Science, 345, 291-296.
    http://dx.doi.org/10.1007/s10509-013-1403-8

  23. 23. Vasyliunas, V.M. (1968) Low-Energy Electrons on the Day Side of the Magnetosphere. Journal of Geophysical Research, 73, 7519-7523.
    http://dx.doi.org/10.1029/JA073i023p07519

  24. 24. Ipavich, F.M., Galvin, A.B., Gloeckler, G., Hovestadt, D., Klecker, B. and Scholer, M. (1986) Comet Giacobini-Zinner: Insitu Observations of Energetic Heavy Ions. Science, 232, 366-369.
    http://dx.doi.org/10.1126/science.232.4748.366

  25. 25. Coplan, M.A., Ogilvie, K.W., A’Hearn, M.F., Bochsler, P. and Geiss, J. (1987) Ion Composition and Upstream Solar Wind Observations at Comet Giacobini-Zinner. Journal of Geophysical Research, 92, 39-46.
    http://dx.doi.org/10.1029/JA092iA01p00039

  26. 26. Chaizy, P., Reme, H., Sauvaud, J.A., d’Uston, C., Lin, R.P., Larson, D.E., Mitchell, D.L., Zwickl, R.D., Baker, D.N., Bame, S.J., Feldman, W.C., Fuselier, S.A., Huebner, W.F., McComas, D.J. and Young, D.T. (1991) Negative Ions in the Coma of Comet Halley. Nature, 349, 393-396.
    http://dx.doi.org/10.1038/349393a0

  27. 27. Zwickl, R.D., Baker, D.N., Bame, S.J., Feldman, W.C., Fuselier, S.A., Huebner, W.F. and Young, D.T. (1986) Three Component Plasma Electron Distribution in the Intermediate Ionized Coma of Comet Giacobini-Zinner. Geophysical Research Letters, 13, 401-404.
    http://dx.doi.org/10.1029/GL013i004p00401

  28. 28. Bhardwaj, A. (2003) On the Solar EUV Deposition in the Inner Coma of Comets with Large Gas Production Rates. Geophysical Research Letters, 30, 2244.
    http://dx.doi.org/10.1029/2003GL018495

  29. 29. Coates, A.J. (1995) Heavy Ion Effects on Cometary Shocks. Advances in Space Research, 15, 403-413.
    http://dx.doi.org/10.1016/0273-1177(94)00125-K

  30. 30. Voelzke, M.R. and Izaguirre, L.S. (2012) Morphological Analysis of the Tail Structures of Comet P/Halley 1910 II. Planetary and Space Science, 65, 104-108.
    http://dx.doi.org/10.1016/j.pss.2012.02.005

  31. 31. Dev, A.N., Sarma, J., Deka, M.K., Misra, A.P. and Adhikary, N.C. (2014) Kadomtsev-Petviashvili (KP) Burgers Equation in Dusty Negative Ion Plasmas: Evolution of Dust-Ion Acoustic Shocks. Communications in Theoretical Phys, 62, 875-880.
    http://dx.doi.org/10.1088/0253-6102/62/6/16

  32. 32. Malfliet, W. (1992) Solitary Wave Solutions of Nonlinear Wave Equations. American Journal of Physics, 60, 650.
    http://dx.doi.org/10.1119/1.17120

  33. 33. Malfliet, W. (2004) The Tanh Method: A Tool for Solving Certain Classes of Nonlinear Evolution and Wave Equations. Journal of Computational and Applied Mathematics, 164, 529-541.
    http://dx.doi.org/10.1016/s0377-0427(03)00645-9

  34. 34. Brinca, A.L. and Tsurutani, B.T. (1987) Unusual Characteristics of the Electromagnetic Waves Excited by Cometary New Born Ions with Large Perpendicular Energies. Astronomy & Astrophysics, 187, 311-319.

NOTES

*Corresponding author.

Journal Menu >>