Received 16 October 2015; accepted 21 December 2015; published 24 December 2015

ABSTRACT

In this paper, we present a novel technique to obtain approximate analytical solution of fractional physical models. The new technique is a combination of a domain decomposition method and natural transform method called a domain decomposition natural transform method (ADNTM). The fractional derivatives are considered in Caputo sense. To illustrate the power and reliability of the method some applications are provided.

Keywords:

Fractional Calculus, Natural Transform, A Domain Decomposition Natural Transform Method (ADNTM), Fokker-Planck Equation, Schrödinger Equation, Kelin-Gorden Equation

1. Introduction

Fractional differential equations have gained importance and popularity, mainly due to its demonstrated applications in science and engineering. For example, these equations are increasingly used to model problems in research areas as diverse as dynamical systems, mechanical systems, control, chaos, chaos synchronization, continuous-time random walks, anomalous diffusive and sub diffusive systems, unification of diffusion and wave propagation phenomenon and others. The most important advantage of using fractional differential equations in these and other applications is their non-local property. It is well known that the integer order differential operator is a local operator but the fractional order differential operator is non-local. This means that the next state of a system depends not only upon its current state but also upon all of its historical states. This is more realistic and it is one reason why fractional calculus has become more and more popular [1] -[11] . The paper is devoted to treatments of nonlinear particular applications that appear in applied sciences. A wide variety of physically significant problems modeled by linear and nonlinear partial differential equations have been the focus of extensive studies for the last decades. A huge size of research and investigation has been invested in these scientific applications. Several approaches have been used such as the characteristics method, spectral methods and perturbation techniques to examine these problems. Nonlinear PDEs have undergone remarkable developments. Nonlinear problems arise in different areas including gravitation, chemical reaction, fluid dynamics, dispersion, nonlinear optics, plasma physics, acoustics, in viscid fluids and others [12] . The rest of paper is organized as follows: in Section 2 we introduce the definition of natural transform and its properties. In Section 3, we show the analysis of ADNTM method. In Section 4, we introduce three applications of ADNTM method for solving fractional nonlinear Fokker-Planck equation, fractional nonlinear Schrödinger equation and fractional nonlinear Kelin- Gorden equation. In Section 5, conclusion is presented.

2. Natural Transform

With reference to the articles [13] [14] , the basic definitions of natural transform and its properties are introduced as follows:

2.1. Definition of Natural Transform

Over the set of functions

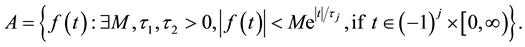
The natural transform of f (t) is defined as:

(1)

where is the natural transformation of the time function and the variables u and s are the natural transform variables.

2.2. Natural-Laplace and Sumudu Duality

If is natural transform and is Laplace transform of function in A then, is Sumudu transform of function in A, then:

2.2.1. Natural-Laplace Duality (NLD) Is

(2)

2.2.2. Natural-Sumudu Duality (NSD) Is

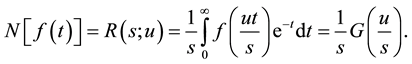(3)

2.3. Natural Transform of nth Derivative

If 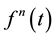is the nth derivative of function 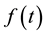then, its natural transform is given by:

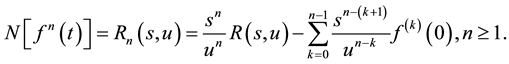(4)

2.4. Convolution Theorem of Natural Transform

If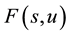, are the natural transform of respective functions, both defined in set A then,

(5)

where is convolution of two functions f and g.

2.5. Natural Transform of Fractional Derivative

If is the natural transform of the function, then the natural transform of fractional derivative

of order is defined as:

(6)

2.6. Weight Shift Property

Let the function belongs to set A be multiplied with weight function then,

(7)

2.7. Change of Scale Property

Let the function belongs to set A, where a is non zero constant then,

(8)

2.8. Natural Transform of Integrals

If is given by

Then the natural transform of 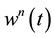is

(9)

2.9. The Natural Transform of T-Periodic Function

The natural transform of T-periodic function such that is given by:

(10)

3. Analysis of Method

To illustrate the basic idea of a domain decomposition natural transform method (ADNTM), we consider the general inhomogeneous nonlinear equation with initial conditions given below [15] :

(11)

where L is the lowest order derivative which is assumed to be easily invertible, R is a linear differential operator of order less than L, FU represents the nonlinear terms and 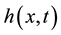is the source term. First, we apply natural transform on both sides of Equation (11):

(12)

Using the differential property of natural transform and initial conditions we get:

By arrangement we have:

(13)

The second step in natural decomposition method is that we represent solution as an infinite series:

(14)

and the nonlinear term can be decomposed as:

(15)

where are A domain polynomial of and it can be calculated by formula:

Substitution of (14) and (15) into (13) yields:

(16)

On comparing both sides of (16) and using standard ADM we have:

Then it follows that:

(17)

In more general, we have:

(18)

On applying the inverse natural transform to (17) and (18), we get:

(19)

where represents the term that is arising from source term and prescribed initial conductions. On using the inverse natural transform to and using the given conditions we get:

where the functions, obtained from a term by using the initial condition is given by:

The terms appears while applying the inverse natural transform on the source term and using the given conditions. We define:

where Then we verify that satisfies the original equation.

4. Applications

4.1. Application 1

Fokker-Plank Equation

The Fokker-Planck equation was first introduced by Fokker and Planck to describe the Brownian motion of particles [16] . This equation has been used in different fields in natural sciences such as quantum optics, solid state physics, chemical physics, theoretical biology and circuit theory. Fokker-Planck equations describe the erratic motions of small particles that are immersed in fluids, fluctuations of the intensity of laser light, velocity distributions of fluid particles in turbulent flows and the stochastic behavior of exchange rates. In general, Fokker- Planck equations can be applied to equilibrium and non equilibrium systems [17] -[20] . The general form of Fractional Fokker-Plank equation is:

(20)

with initial condition

where is an unknown function, A(x) and B(x) are called diffusion and drift coefficients such that. The diffusion and drift coefficients in Equation (20) can be functions of x and t as well as:

(21)

Equation (20) is also well known as a forward Kolmogorov equation. There exists another type of this equation is called a backward one as [16] :

(22)

A generalization of Equation (20) to N-variables of yields to

(23)

with the initial condition

The nonlinear Fokker-Planck equation is a more general form of linear one which has also been applied in vast areas such as plasma physics, surface physics, and astrophysics the physics of polymer fluids and particle beams, nonlinear hydrodynamics, theory of electronic-circuitry and laser arrays, engineering, biophysics, population dynamics, human movement sciences, neurophysics, psychology and marketing [21] .

The nonlinear form of the Fokker-Planck equation can be expressed in the following form:

(24)

A generalization of Equation (24) to N-variables of yields to

(25)

Now, we consider the following nonlinear Fokker-Planck equation:

(26)

(27)

Then, Equation (26) becomes:

(28)

with initial condition

According to ADNTM, by applying natural transform of both sides of Equation (28) and using the initial condition we get:

(29)

The second step in natural decomposition method is that we represent solution as an infinite series:

(30)

i.e.

Then, recursive relations are:

and nonlinear terms can be decomposed as:

are domain polynomials of [10] and they can calculate by formula, and they can calculate by formula

(31)

(32)

(33)

According to ADM we have

Hence

(34)

At special case, when we obtain [see Figure 1]:

(35)

which is the exact solution and is same as obtain by ADM [22] , VIM [23] , and HPM [24] .

4.2. Application 2

Schrodinger Equation

Nonlinearly interacting waves are often described by asymptotic equations [12] . The most basic asymptotic equation is probably the nonlinear Schrödinger equation, which gained its importance because of its appearance in many scientific applications and physical phenomena. It is used in wave mechanics to describe a physical system. Solutions of this equation are wave-functions for which the square of the amplitude expresses the probability density for a particle or a set of particles. If the system is isolated then a time-independent form of the equation is applicable. Solution for this version for bound particles shows that the energy for the system must be quantized. Now, we consider the following cubic nonlinear Schrödinger equation [25] :

(36)

with initial condition

The exact solution at is

By applying natural transform of Equation (36), we obtain:

Using the differential property of natural transform and initial conditions we get:

(37)

The second step in natural decomposition method is that we represent solution as an infinite series:

(38)

and the nonlinear term can be decomposed as:

(39)

where are A domain polynomial of and it can be calculated by formula

Substitution of (39) and (38) into (37) yields

(40)

where nonlinear term is given by

(41)

In view of (41), and following the formal techniques used before to derive the a domain polynomials, we can easily derive that F(u) has the following polynomials representation:

On comparing both sides of (40) and using standard ADM we have:

(42)

(43)

According to ADM we have

Hence,

(44)

At special case, when we obtain [see Figure 2 and Figure 3]

(45)

which is the exact solution of (36) by [26] .

4.3. Application 3

Kelin-Gorden Equation

The Klein-Gordon equation [27] [28] is considered one of the most important mathematical models in quantum field theory. The equation appears in relativistic physics and is used to describe dispersive wave phenomena in general. In addition, it also appears in nonlinear optics and plasma physics. The Klein-Gordon equation arise in physics in linear and nonlinear forms. The Klein-Gordon equation has been extensively studied by using traditional methods such as finite difference method, finite element method, or collocation method. Backlund transformations and the inverse scattering method were also applied to handle Klein-Gordon equation. The objectives of these studies were mostly focused on the determination of approximate analytical solution of Klein-Gordon equation in fractional order and reducing the volume of the computational work as compared to the classical methods while still maintaining the high accuracy of the numerical result amounts to an improvement of the performance of the approach. Now, we consider the following nonlinear Klein-Gordon equation [27] :

(46)

with the initial conditions

As the previous, by applying ADNTM method, we have:

(47)

(48)

(49)

According to ADM we have

Hence

(50)

which is the exact solution as obtained by VIM [29] and HPTM [30] .

4.4. Figures

5. Conclusion

As shown in the three examples of this paper, the domain decomposition natural analytical solutions of time- fractional Fokker-Planck equation, time-fractional Schrödinger equation, and time fractional Kelin-Gorden equation were in excellent agreement with the exact solutions. Finally, generally speaking, the proposed method can be further implemented to solve other physical models in fractional calculus field.

Acknowledgements

We thank Directors, Department of Mathematics, Faculty of Science, South Valley University, Qena, Egypt and Department of Mathematics and Computer Science, Faculty of Science, Port Said University, Port Said, Egypt for their cooperation during this work.

Cite this paper

Ahmed SafwatAbdel-Rady,Saad ZagloulRida,Anas Ahmed MohamedArafa,Hamdy RagabAbedl-Rahim, (2015) Natural Transform for Solving Fractional Models. Journal of Applied Mathematics and Physics,03,1633-1644. doi: 10.4236/jamp.2015.312188

References