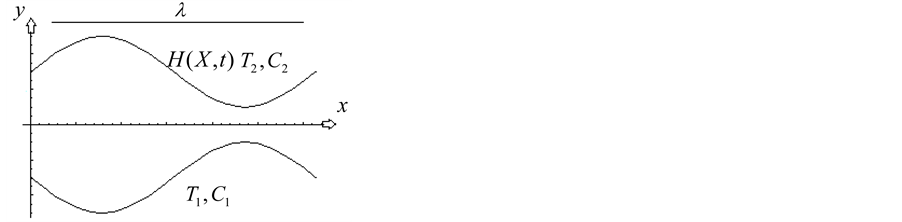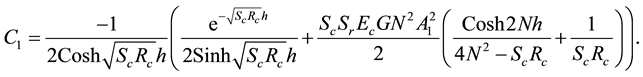Journal of Applied Mathematics and Physics
Vol.03 No.09(2015), Article ID:59717,12 pages
10.4236/jamp.2015.39141
Hall Effect on Peristaltic Flow of Third Order Fluid in a Porous Medium with Heat and Mass Transfer
Nabil T. M. Eldabe, Ahmed Y. Ghaly, Sallam N. Sallam, Khaled Elagamy, Yasmeen M. Younis
Department of Mathematics, Faculty of Education, Ain Shams University, Cairo, Egypt
Email: Mohamed.unis@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 July 2015; accepted 15 September 2015; published 18 September 2015
ABSTRACT
We investigated the influence of hall, heat and mass transfer on the peristaltic flow of MHD third order fluid under long-wavelength and low Reynolds number approximation. The governing equations are solved analytically with the appropriate boundary conditions by using perturbation technique. The formula of velocity with temperature and concentration is obtained analytically as a function of the physical parameters of the problem.
Keywords:
Peristaltic Flow, Third Order Fluid, Hall Effect, Heat, Mass Transfer

1. Introduction
Many fluids in biological system are transported by peristalsis. The word peristalsis stems from the Greek word peristaltikos, which means clasping and compressing. Physically, it means the mechanism for pumping fluid in a tube by means of a moving contractile ring around the tube, which pushes the material onward. The need for peristaltic pumping may arise in circumstances where it is desirable to avoid using any internal moving parts such as pistons to be one of the main mechanisms of fluid transport in a biological system. The application of peristaltic motion as a mean of transporting fluid has aroused interested in engineering fields. Latham [1] was probably the first to study the mechanism of peristaltic pumping in his M. S. Thesis. Several researches have analyzed the phenomenon of peristaltic transport under various assumptions. Haroun [2] studied the effect of a third-order fluid on the peristaltic transport in an asymmetric channel. In his study, the wavelength of the peristaltic waves is assumed to be large compared to the varying channel width, whereas the wave amplitudes need not be small compared to the varying channel width. Eldabe et al. [3] analyzed the incompressible flow of electrically conducting biviscosity fluid through an axisymmetric nonuniform tube with a sinusoidal wave under the considerations of long wavelength and low Reynolds number.
In the last years, several simple flow problems of classical hydrodynamics have received new attention in the more general context magnetohydrodynamics (MHD). The study of the motion of non-Newtonian fluids in the presense of the magnetic field has applications in many devices such as magneto hydrodynamic (MHD) power generator, MHD pumps, bioengineering devices and accelerators. Also it has been established that the biological systems are greatly affected by the application of the external magnetic field. Moreover, the MHD flow of a fluid in a channel with elastic, rhythmically contracting walls (peristaltic flow) is of interest in connection with certain problems of the movement of conductive physiological fluids. Some recent investigations made to discuss the mechanism of MHD include the works. Hayat et al. [4] studied the peristaltic transport of a third order fluid under the effect of a magnetic field. Srinivas and Kothandapani [5] have studied the influence of heat and mass transfer on MHD peristaltic flow through a porous space with compliant walls. Another important aspect in MHD is related to Hall effect. Such effect cannot be overlooked when flow subject to high magnetic field is considered. Siddiqui et al. [6] studied effects of Hall current and heat transfer on MHD flow of a Burgers fluid due to a pull of eccentric rotating disks. Hall effects on peristaltic flow of a Maxwell fluid in a porous medium have been studied by Hayat et al. [7] studied effects of Hall current and heat transfer on rotating flow of a second grade fluid through a porous medium. Khalid Nowar [8] studied Peristaltic Flow of a Nanofluid under the effect of Hall Current and Porous Medium.
The study of the influence of mass and heat transfer on non-Newtonian fluids has become important in the last few years. This importance is due to number of industrial processes. Examples are food processing, biochemical operations and transport in polymers, biomedical engineering; micro fabrication technologies etc., besides these biological tissues with heat transfer involve modes like heat conduction in tissues, heat convection by blood flow through the pores of tissue and radiation heat transfer between surface and its environment. Motivated by such facts, the peristaltic flow with heat transfer has been explored. El-Dabe et al. [9] studied magnetohydrodynamic flow and heat transfer for a peristaltic motion of carreau fluid through a porous medium. El-Dabe et al. [10] studied Peristaltic Motion of Non-Newtonian Fluid with Heat and Mass Transfer through a Porous Medium in Channel under Uniform Magnetic Field. El-Dabe et al. [11] analyzed the Magnetohydrodynamic Peristaltic motion with heat and mass transfer of a Jeffery fluid in a tube through porous medium.
With the above discussion in mind, we propose to study the peristaltic motion of non-Newtonian fluid through a porous medium in the channel under the effect of magnetic field. A third order non-Newtonian constitutive model is employed for the transport fluid. The effects of hall, body temperature and concentration are taken into consideration. The governing equations of motion, energy, and concentration have been reduced under the assumption of long wavelength. The reduced equations are then solved analytically via perturbation method. The physical behaviors of emerging parameters are discussed through graphs.
2. Mathematical Analysis
Consider a two-dimensional channel of uniform thickness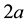 , filled with incompressible homogeneous electrically conducting non-Newtonian third order fluid through a porous medium with heat and mass transfer. The channels walls are considered and flexible the vertical displacements for the upper and lower walls are
, filled with incompressible homogeneous electrically conducting non-Newtonian third order fluid through a porous medium with heat and mass transfer. The channels walls are considered and flexible the vertical displacements for the upper and lower walls are 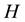 and
and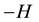 , see Figure 1, where
, see Figure 1, where 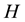 is defined by
is defined by
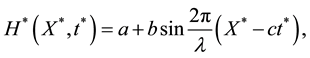 (1)
(1)
where In the above equation 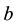 is the wave amplitude,
is the wave amplitude, 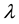 is the wave length and
is the wave length and 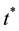 is the time. A uniform magnetic field with magnetic flux density vector
is the time. A uniform magnetic field with magnetic flux density vector 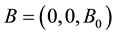 is applied, neglecting the induced magnetic field under the assumption that the magnetic Reynolds number is small, the expression for the current density
is applied, neglecting the induced magnetic field under the assumption that the magnetic Reynolds number is small, the expression for the current density 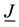 including the Hall effect and neglecting ion-slip and thermoelectric effects is given by
including the Hall effect and neglecting ion-slip and thermoelectric effects is given by
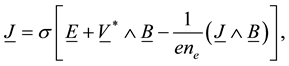 (2)
(2)
where 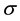 is the electric conductivity of the fluid is,
is the electric conductivity of the fluid is, 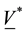 is the velocity vector, It is also assumed that
is the velocity vector, It is also assumed that 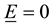
Figure 1. Sketch of the problem.
(since there is no applied polarization voltage), 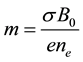 is the Hall parameter,
is the Hall parameter, 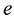
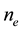
Consider

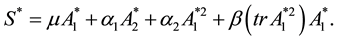
Here 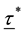
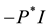

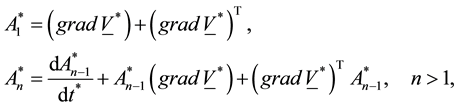
where grad denotes the gradient operator, 

cosity, the normal stress coefficients 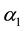
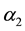

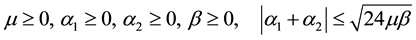
The fundamental equations governing this model together with the generalized Ohm’s law taking the effects of Hall currents and Maxwell’s equations into account are
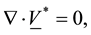
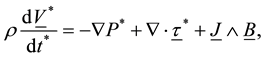

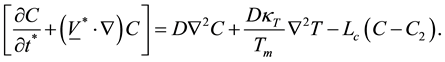
where 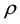

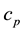
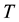
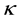
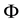
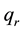

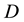
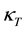
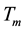
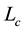
By using Rosselant approximation we have

where 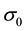
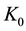
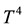
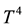
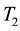
The equations governing the two-dimensional motion of this model (7)-(10)
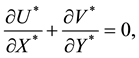

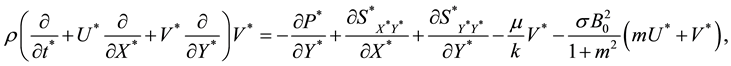
where
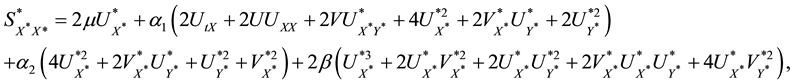
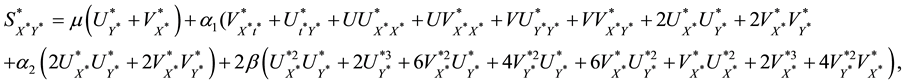
and
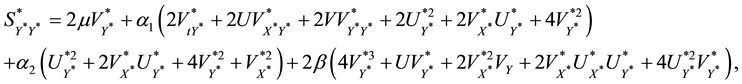
where 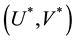
The dissipation function 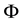
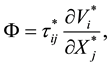
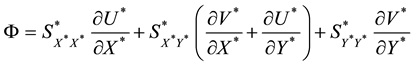
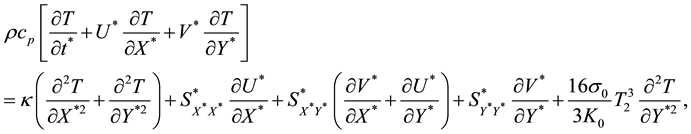
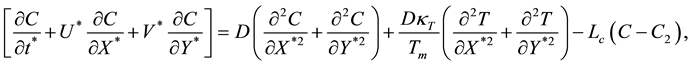
The appropriate boundary conditions taken as follows:
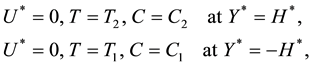
Consider a wave frame 
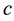
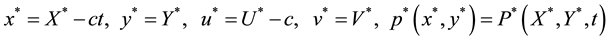
In which 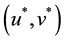
Then, the system of Equations (12)-(22) can be written as:
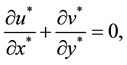

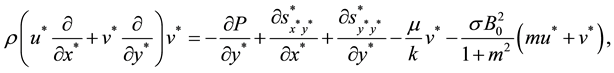
where


And
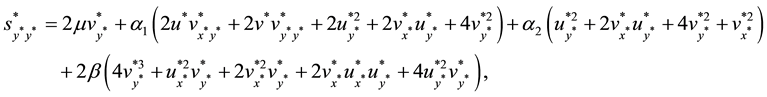
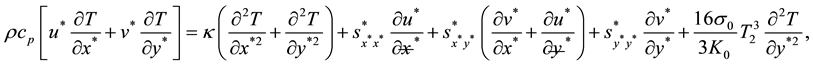

The boundary conditions become:
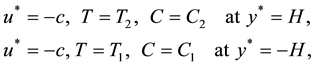
We introduce the following non-dimensional quantities:
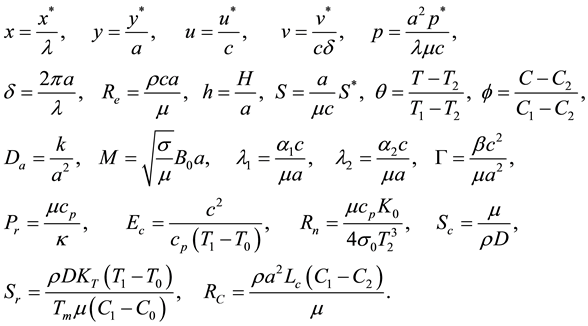
where the non-dimensional wave number
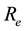
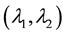
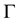
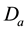
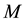
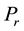

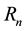
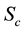
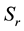

Substituting (33) into Equations (24)-(32) we obtain the following non-dimensional equations:
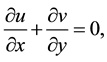
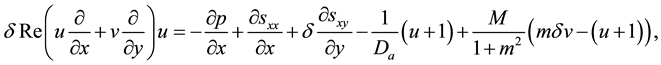
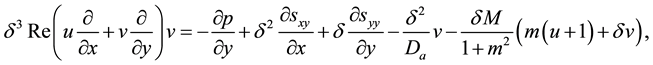
where


and
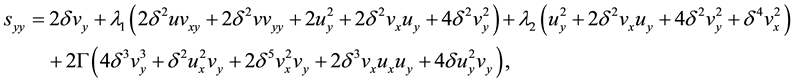

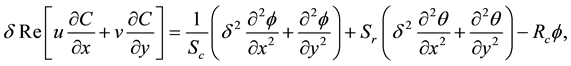
With conditions:
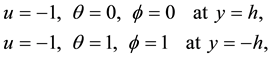
We also note that 

where, 
under the assumptions of long wavelength

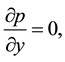





Eliminating 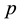
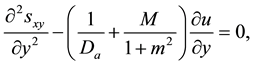
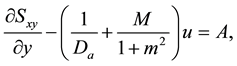

3. Series Solution
For perturbation solution we write

Substituting (52) in the Equations (45)-(49), equating the coefficients of like powers of
Zeroth order system:


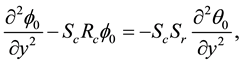
The subjected boundary conditions are:
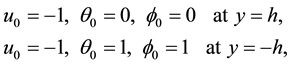
First order system
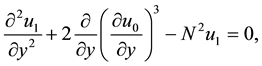
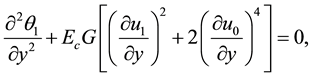
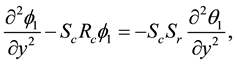
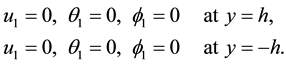
The solution of zero order system can be obtained analytically as

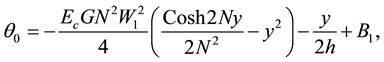
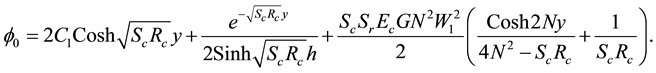
Also, the solution of first order system can be obtained analytically as


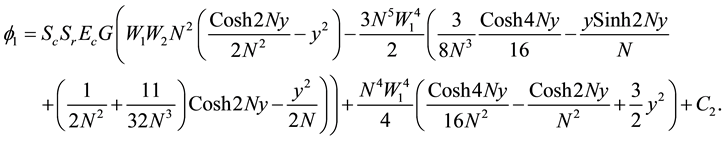
where
4. Results and Discussion
In order to obtain the physical insight of the problem, velocity, temperature and concentration are computed numerically for different values of the emerging parameters, viz., Darcy number is


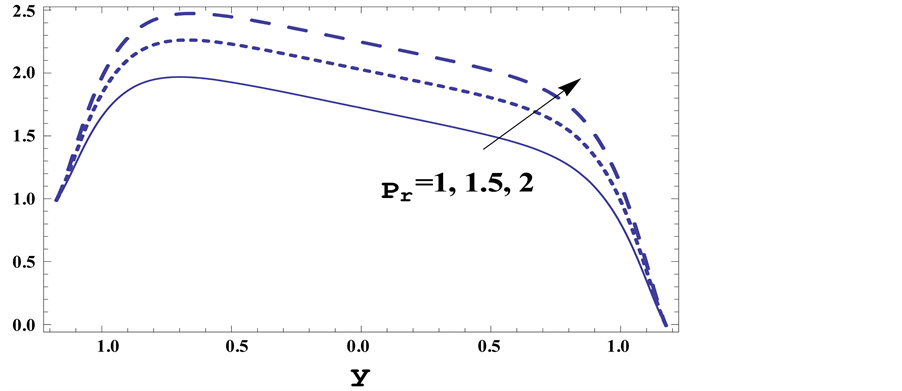
Figure 2. Velocity profiles 
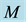
Figure 3. Velocity profiles 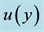
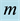
Figure 4. Velocity profiles 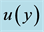
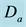
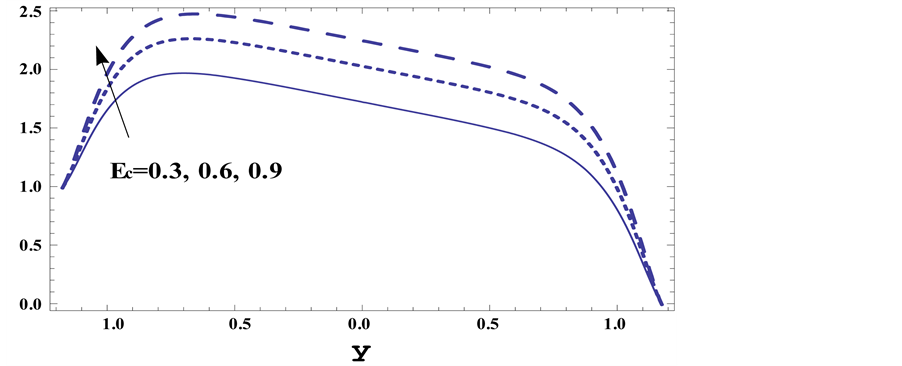
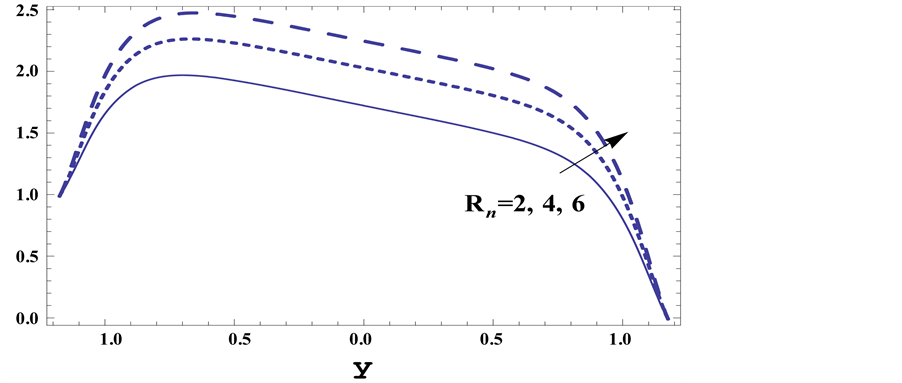
Figure 5. Temperature profiles 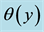
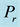
Figure 6. Temperature profiles 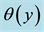

Figure 7. Temperature profiles 

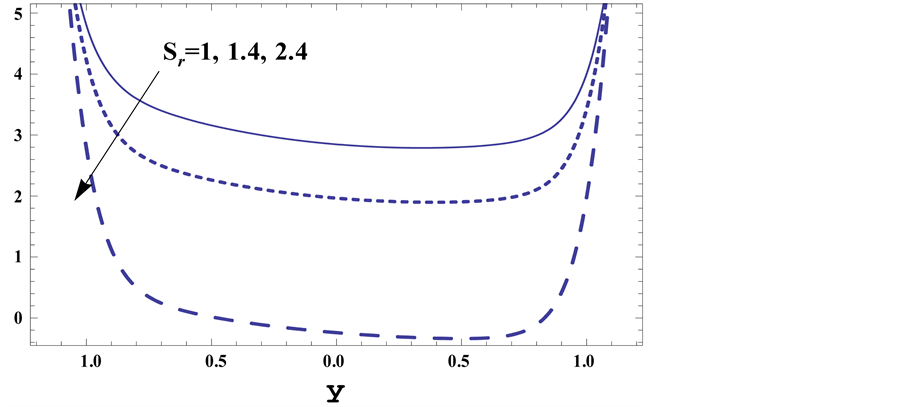
Figure 8. Concentration profiles 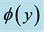
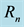
Figure 9. Concentration profiles 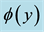
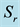
Figure 10. Concentration profiles 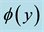

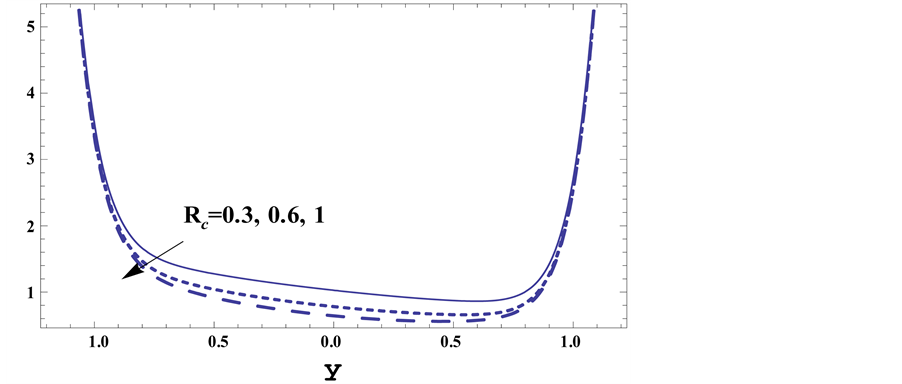
Figure 2 presents the effect of Hartman number 
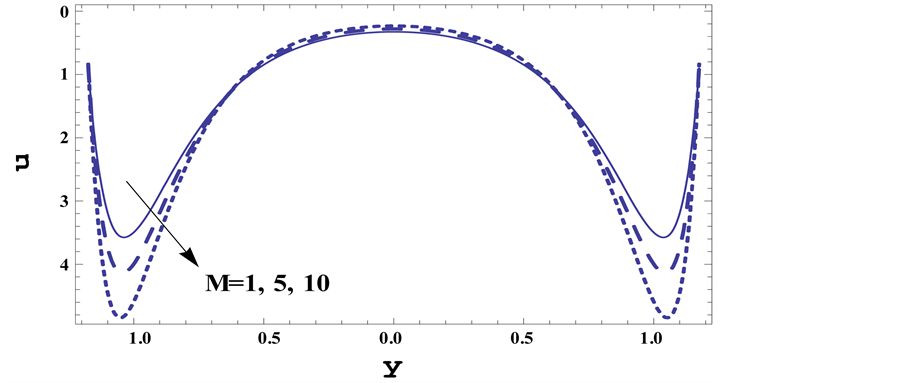
Figure 3 shows the effect of the Hall parameter m on the velocity. It is observed that as m increases the velocity decreases in the interval [−0.6, 0.6] and vice versa in the other intervals.
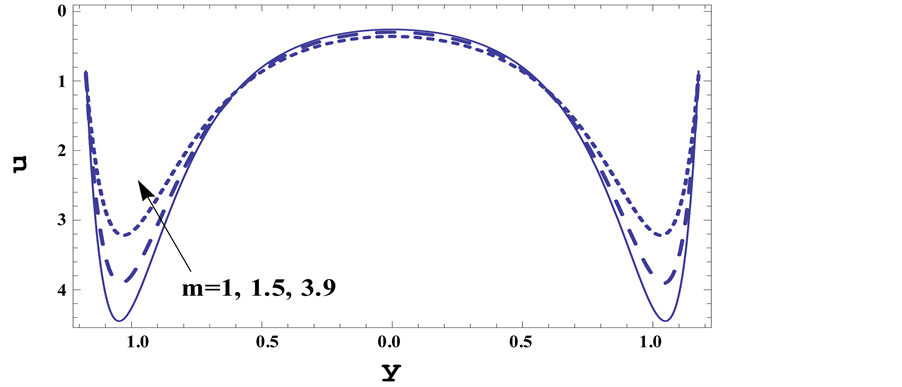
Figure 4 shows the effect of Darcy parameter 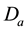
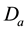
Figures 5-7 describe the effect of different parameters on the temperature distribution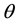

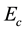
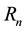
Figures 8-10 display results for the concentration 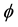
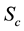
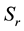
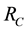
5. Conclusions
In this paper, we studied the effects of the physical parameters of the considered problem on peristaltic transport in a tube, filled with an incompressible non-Newtonian (Third order) fluid, and considered the effects of hall current, body temperature and concentration. The system is solved analytically by perturbation technique. The effects of various emerging parameters on the flow, the temperature and the concentration distributions are shown and discussed with the help of graphs. The main findings can be summarized as follows.
1) The velocity decreases in the interval [−0.6, 0.6] and vice versa in the other intervals with the increase of each of 
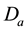
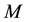
2) The temperature 
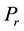
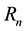
3) The concentration decreases as the Schmidt number


Caption of Figures
Figure 2 the velocity profiles are plotted versus 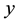
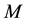
lars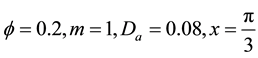
Figure 3 the velocity profiles are plotted versus 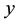

lars
Figure 4 the velocity profiles are plotted versus 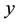
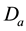
culars
Figure 5 the temperature profiles are plotted versus 
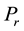
ticulars
Figure 6 the temperature profiles are plotted versus 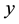
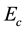
particulars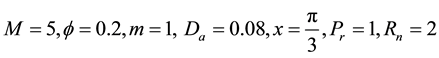
Figure 7 the temperature profiles are plotted versus 
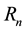
particulars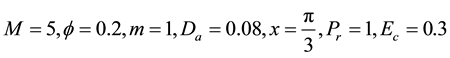
Figure 8 The concentration profiles are plotted versus 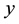
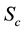
particulars
Figure 9 the concentration profiles are plotted versus 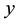

particulars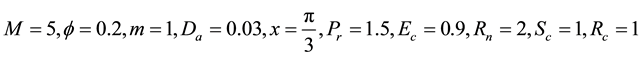
Figure 10 the concentration profiles are plotted versus 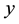

particulars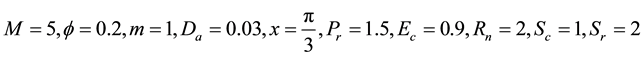
Cite this paper
Nabil T. M.Eldabe,Ahmed Y.Ghaly,Sallam N.Sallam,KhaledElagamy,Yasmeen M.Younis, (2015) Hall Effect on Peristaltic Flow of Third Order Fluid in a Porous Medium with Heat and Mass Transfer. Journal of Applied Mathematics and Physics,03,1138-1150. doi: 10.4236/jamp.2015.39141
References
- 1. Latham, T.W. (1966) Fluid Motions in a Peristaltic Pump, M.S. Thesis, M.I.T., Cambridge.
- 2. Haroun, M.H. (2007) Effect of Deborah Number and Phase Difference on Peristaltic Transport of a Third-Order Fluid in an Asymmetric Channel. Communications in Nonlinear Science and Numerical Simulation, 12, 1464-1480.
http://dx.doi.org/10.1016/j.cnsns.2006.03.002 - 3. Eldabe, N.T.M., El-Sayed, M.F., Ghaly, A.Y. and Sayed, H.M. (2007) Peristaltically Induced Transport of a MHD Biviscosity Fluid in a Non-Uniform Tube. Physica A, 383, 253-266.
http://dx.doi.org/10.1016/j.physa.2007.05.027 - 4. Hayat, T., Afsar, A., Khan, M. and Asghar, S. (2007) Peristaltic Transport of a Third Order Fluid under the Effect of a Magnetic Field. Computers and Mathematics with Applications, 53, 1074-1087.
http://dx.doi.org/10.1016/j.camwa.2006.12.014 - 5. Srinivas, S. and Kothandapani, M. (2009) The Influence of Heat and Mass Transfer on MHD Peristaltic Flow through a Porous Space with Compliant Walls. Applied Mathematics and Computation, 213, 197-208.
http://dx.doi.org/10.1016/j.amc.2009.02.054 - 6. Siddiqui, A.M., Rana, M.A. and Ahmed, N. (2008) Effects of Hall Current and Heat Transfer on MHD Flow of a Burgers’ Fluid Due to a Pull of Eccentric Rotating Disks. Communications in Nonlinear Science and Numerical Simulation, 13, 1554-1570.
http://dx.doi.org/10.1016/j.cnsns.2006.10.005 - 7. Hayat, T., Abbas, Z. and Asghar, S. (2008) Effects of Hall Current and Heat Transfer on Rotating Flow of a Second Grade Fluid through a Porous Medium. Communications in Nonlinear Science and Numerical Simulation, 13, 2177-2192.
http://dx.doi.org/10.1016/j.cnsns.2007.03.033 - 8. Nowar, K. (2014) Peristaltic Flow of a Nanofluid under the Effect of Hall Current and Porous Medium. Mathematical Problems in Engineering, 2014, 1-15.
http://dx.doi.org/10.1155/2014/389581 - 9. Eldabe, N.T.M., Fouad, A. and Hussein, M.M. (2010) Magnetohydrodynamic Flow and Heat Transfer for a Peristaltic Motion of Carreau Fluid through a Porous Medium. Journal of Mathematics, 42, 1-16.
- 10. Eldabe, N.T.M., Agoor, M. and Alame, H. (2014) Peristaltic Motion of Non-Newtonian Fluid with Heat and Mass Transfer through a Porous Medium in Channel under Uniform Magnetic Field. Journal of Fluids, 2014, 1-12.
http://dx.doi.org/10.1155/2014/525769 - 11. Eldabe, N.T.M., Sallam, N.S., Mohamed, M.A.A, Abo Zaid, M.Y. and Abd-Elmonem, A. (2011) Magnetohydrodynamic Peristaltic Motion with Heat and Mass Transfer of a Jeffery Fluid in a Tube through Porous Medium. Innovative Systems Design and Engineering, 264-275.