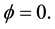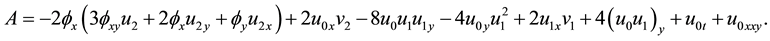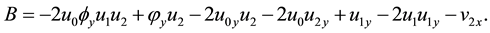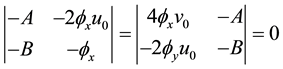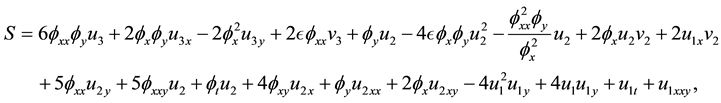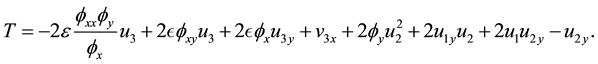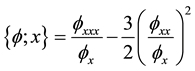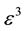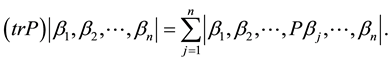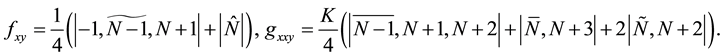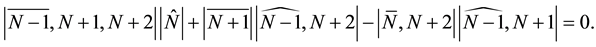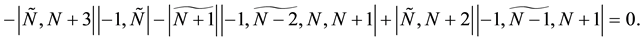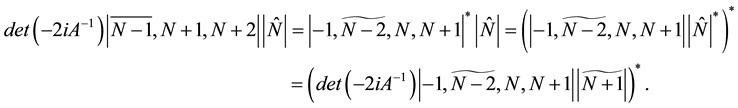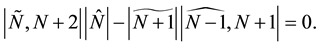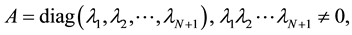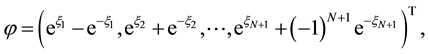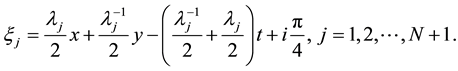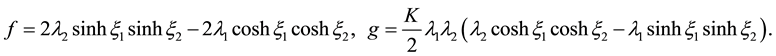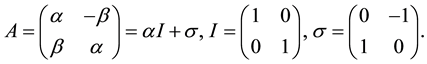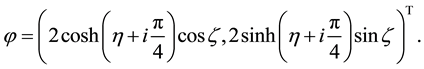Received 12 May 2015; accepted 27 June 2015; published 30 June 2015

ABSTRACT

A (2 + 1) dimensional KdV-mKdV equation is proposed and integrability in the sense of Painlevé and some exact solutions are discussed. The Bäcklund transformation and bilinear equations are obtained through Painlevé analysis. Some exact solutions are deduced by Hirota method and generalized Wronskian method.

Keywords:

(2+1) Dimensional KdV-mKdV Equation, Painlevé Property, Bäcklund Transformation, Bilinear Equation, Wronskian Method

1. Introduction

Recently high dimensional nonlinear partial differential or difference equations attract much interest. Both inte- grable and non-integrable equations have their physical and mathematical values but the former posses some special properties such as infinite conservation laws and symmetries, multi-soliton solutions, Bäcklund and Darboux transformation (c.f. [1] - [3] ). Among these high dimensional equations some are deduced from physics phenomenon originally, say KP equation, but others are deduced firstly from (1 + 1) dimensional equation mathematically ( [4] - [8] ). However, the findings of new solutions or special constructions of these equations makes nonlinearity of equations be realized clearly, which helps the development of subject of nonlinear science. In this paper we will consider a (2 + 1) dimensional KdV-mKdV equation as follows

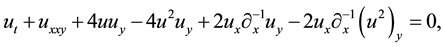(1)

where subscript means a partial derivative such as and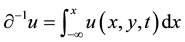. It is obvious

that if 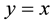the equation becomes a mixed KdV-mKdV equation, which is widely researched by many authors (see [7] - [10] ). The related negative KdV equation and (2 + 1)-dimensional KdV equation were also discussed by several authors (c.f. [11] - [14] ). Now we set

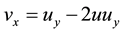(2)

to treat the integral appearing in equation. The Equation (1) is then rewritten as

(3)

We will prove it has Painlevé property firstly, then deduce a Bäcklund transformation and bilinear equation. Using bilinear equation we can construct Wronskian solutions and present some exact solutions finally.

2. Painlevé Test

Painlevé analysis method is an important method for testing integrability [15] - [19] . As we know, the basic Painlevé test consists of the following steps (taking (1 + 1) dimensional case as an example) [15] [19] .

Step 1. Expanding the solution of a PDE as Laurent series of a singular manifold

where is constant to be determined and coefficients 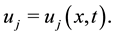Then substitute it into PDE to find all dominant balances.

Step 2. If all exponents 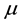are integers, find the resonances where arbitrary constants can appear.

Step 3. If all resonances are integers, check the resonance conditions in each Laurent expansion.

Conclusion. If no obstruction is found in Steps 1 - 3 for every dominant balances, then the Painlevé test is satisfied.

The situation of high dimensional case is similar. For step 1, we can simply let

(4)

Substituting them into (2, 3) gives us

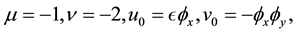(5)

where 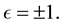Thus

(6)

Insert them into (2, 3) and equal coefficients of both side of 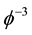in (3), 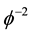in (2) we have

(7)

(8)

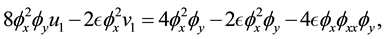
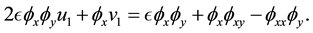
From them we work out

(9)

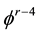
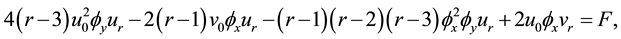
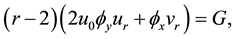
To get resonances we collect the coefficient of in (3), in (2) for general term number r respec- tively, we have

(10)

(11)

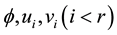
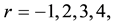
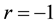
where F, G are functions of and their derivatives. This gives the resonances and means the singular manifold

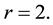
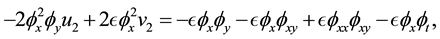
Now we proceed to verify the resonance conditions. First we consider For this purpose we extract in (3) and set it be zero. We readily have

(12)

or equivalently

(13)

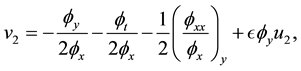
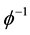
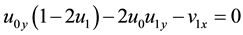
The part of in (2) gives

(14)

and it is true by employing obtained above. This result shows that an arbitrary appears in reso- nance, i.e. resonance condition is satisfied. Further, we verify resonance condition for Collecting the terms of in (3) reads

(15)

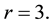
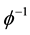
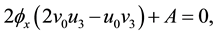
where

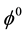
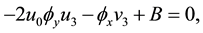
In a similar way, collecting the terms of in (2) makes us have

(16)

where

we need to verify

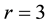
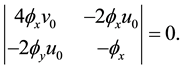
because is a resonance, i.e. By inserting (13) into and through a dull calculation

we can complete the proof of compatible condition. It is a turn to consider which emerge from in (3) and in (2). They are

(17)

where

and

(18)

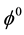
where

Its resonance condition is verified similarly but is more complex. Thus we prove that (2 + 1) dimensional KdV-mKdV equation passes Painlevé test.

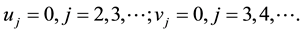
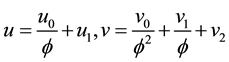
Now we consider to truncate the series (6). To meet this end we must let Thus we will have

(19)

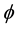
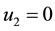
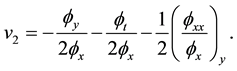
and combine the equation satisfied by we obtain a Bäcklund transformation actually. In fact, if we take then (13) gives

(20)

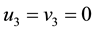
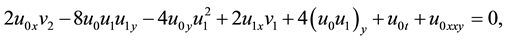
Furthermore, If we continue to set we get following relations from (15, 16)

(21)

and

(22)

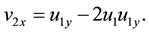
The condition 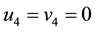produces another identity

(23)

Using (20)-(23) we may truncate the series. Thus we indeed get a Bäcklund transformation by noting (22, 23). But it is more important pointing that the identities (20)-(23) have only two independent expressions, say (22, 23). Applying the definition of Schwartzian derivative

we simplify them as a concise form, i.e. so called Schwartzian derivative equation

(24)

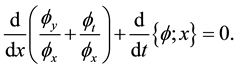
It is the condition satisfied by function 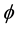in Bäcklund transformation (19).

3. Hirota Method for Finding Exact Solutions

In this section we will give the bilinear equation of Equation (1) and present some exact solutions from it. The truncation form (19) suggests us to try the transformation

(25)

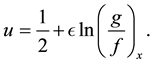
We first take an integral with respect to x on Equation (1). Then eliminate the remaining integral operator by setting

(26)

where D is bilinear operator. Thus we can transfer Equation (1) into

(27)

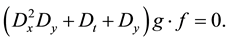
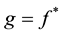
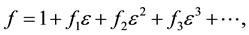
Equations (26, 27) are bilinear equations of (1). To find its solutions we set further, where ^* means complex conjugation. Expanding f as perturbation series

(28)

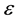
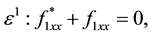
and substituting it into bilinear equations, equaling coefficients of power of yields

(29)

(30)

Take

(31)

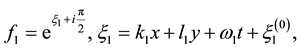
where and are all real constants (the similar condition will be imposed on later text but omitting), we know the relation immediately

(32)

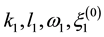
The coefficient of 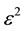can take as zero according to this result. So we get a single solution solution as follows

(33)

If we take

(34)

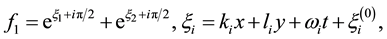
then after substituting it into (29, 30) we know relations

(35)

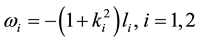
are valid. Again compare coefficient of, we have

(36)

(37)

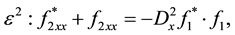
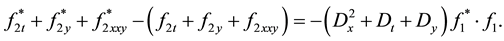
When employing (34),

(38)

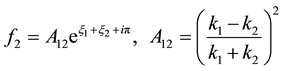
are obtained. After that we consider coefficient of

(39)

(40)

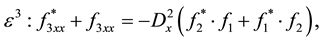
The r.h.s is computed to zero. Thus we may truncate the perturbation series and 2-soliton solution is got as

(41)

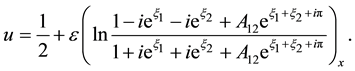
Further, keeping these results in mind we can conjecture the N-soliton solution taking on

(42)

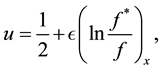
where 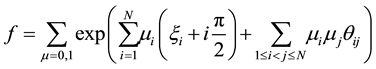and

4. Wronskian Solutions

Wronskian technique is one of the powerful methods in finding exact solutions of nonlinear integrable evolution equation [20] [21] . It can be used to solve whole integrable evolution equation hierarchy (c.f. [22] [23] ) and its application had been extended to negative nonlinear evolution equation (c.f. [23] [24] ), high dimensional nonlinear evolution equation [25] , etc. The generalization of this method can obtain several types of exact solutions (c.f. [26] [27] ). Here we use the Nimmo's brief notation to denote Wronskia determinants:

and

where 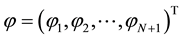and

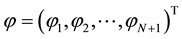
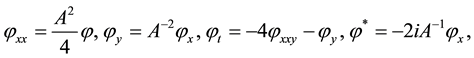
Supposing that vectors satisfies the following conditions

(43)

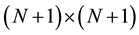
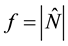
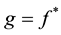
where A is a non-singular real constant matrix. We will prove that is the solution of bilinear Equations (26) and (27). We first point out that in this situation, can be expressed by related Wronskia determinant:

To get down to our work we need the help of two Lemmas, we list out them first.

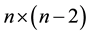
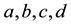
Lemma 1 ( [26] [27] ) Assuming that M is a matrix and are n-dimensional vectors, then the following determinantal identity is valid:

Lemma 2 ( [23] [24] ) Assuming P is a 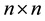matrix, are the columns of another matrix, then we have the following foluma

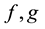
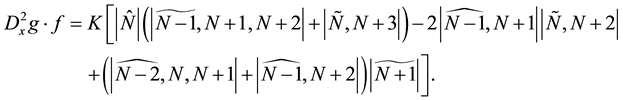
We first treat bilinear Equations (26). Computing derivatives of Wronskians and substituting them into (26) yields

(44)

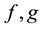
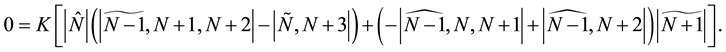
When apply Lemma 2 into Wronskians we get an identity as follows

(45)

Then adding it to (44) gives us

(46)

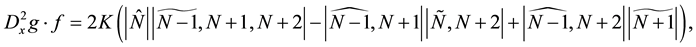
which equals zero by using Lemma 1. Now we can focus our attention on the bilinear Equation (27). We also calculate the derivative of Wronskians prior to carrying out our procedure. For example, we have

Then becomes as

(47)

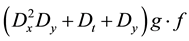
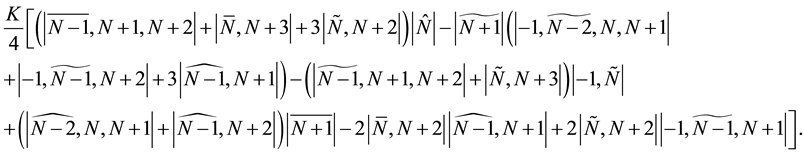
Again using Lemma 2, we produce two identities as follows:

(48)

(49)

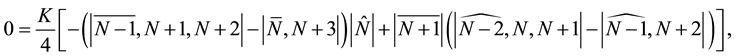
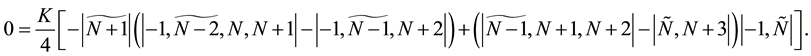
The substitution of (48, 49) into (47) yields

(50)

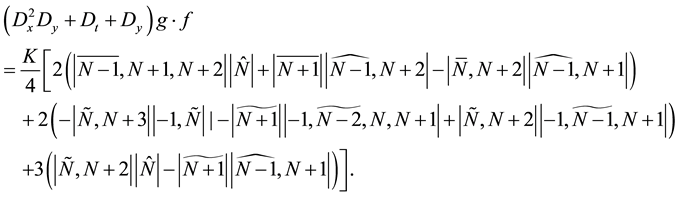
To vanish r.h.s of this equation we apply Lemma 1 again, which give us a valuable identity

Multiply 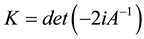to this identity we work out another relation as follows:

It is because of

In a same way, we deduce

Thus we complete the proof that

Now we present some exact solutions as examples. Firstly, we may write out the expression of spectral vector: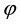

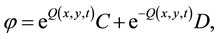
(51)

where are two real constant vectors and

(52)

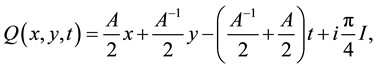
where I is 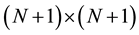unit matrix. If we choose A as diagonal matrix then soliton solutions of equation (1) can be got again. In fact, supposing

and

then spectral vector adopts the following formula

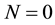
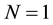
The solutions given by (25) are solitons solutions in this situation. In fact, when, it is exactly the solution (33). When consider, we compute out

This gives the same solution as (41) or simplified form:

(53)

which is a two-soliton solution. We can also take into account other solutions. For instance, let

Then we find in this situation:

(54)

(55)

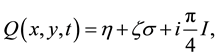
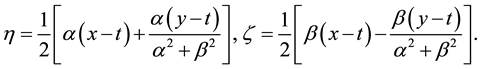
Taking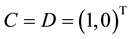, the spectral vector is got then:

The correspondent solution of Equation (1) is

(56)

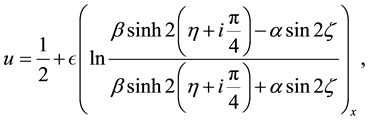
or simplified form

(57)

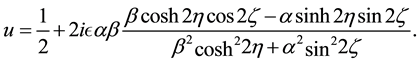
This is known as a complexiton solution (c.f. [26] ).

5. Conclusion

Utilizing Painlevé test we prove the integrability of a (2 + 1) dimensional KdV-mKdV equation in the sense of Painlevé. And in the mean time a Bäcklund transformation is produced. Through bilinear equation we get several exact solutions by Hirota method and generalized Wronskian method. Some explicit formulas of exact solutions are obtained. Particularly, 2-soliton solution and complexiton solutions are presented as examples.

Acknowledgements

The authors are grateful to editors and referees for their very careful works. In the mean time, the authors thank to the referees for giving helpful advices.

Support

This work is partly supported by Chinese National Social Science Foundation (Grant Number: CNSSF: 13CJY037) Research on the indemnificatory Apartment Construction Based on Residential Integration.

References

NOTES

^*Corresponding author.