Journal of Applied Mathematics and Physics
Vol.02 No.13(2014), Article ID:52521,4 pages
10.4236/jamp.2014.213141
The Rise of Solitons in Sine-Gordon Field Theory: From Jacobi Amplitude to Gudermannian Function
Leonardo Mondaini1,2
1Department of Oncology, University of Alberta, Edmonton, Canada
2Grupo de Física Teórica e Experimental, Departamento de Ciências Naturais, Universidade Federal do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
Email: mondaini@ualberta.ca, mondaini@unirio.br
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 November 2014; revised 30 November 2014; accepted 6 December 2014
ABSTRACT
We show how the famous soliton solution of the classical sine-Gordon field theory in (1 + 1)-di- mensions may be obtained as a particular case of a solution expressed in terms of the Jacobi amplitude, which is the inverse function of the incomplete elliptic integral of the first kind.
Keywords:
Solitons, Sine-Gordon Field Theory, Elliptic Integrals, Jacobi Amplitude

1. Introduction
The sine-Gordon field theory and the associated massive Thirring model [1] are some of the best studied quantum field theories. In view of its connections to other important physical models, some of which in principle admit actual realizations in nature [2] [3] , a huge mass of important exact results have been obtained for this fascinating integrable system [4] - [7] . However, no less fascinating are the remarkable mathematical and physical properties of its soliton (or “solitary wave”) solutions which have contributed, along the last decades, to turning the physics of solitons into a very active research topic.
In this work we present a simple and yet appealing step-by-step derivation of a more general solution for the classical sine-Gordon field theory in (1 + 1)-dimensions in terms of a special kind of elliptic function, namely the Jacobi amplitude, which has the famous sine-Gordon soliton solution as a particular case. Despite the fact that the connection between solitons and Jacobi elliptic functions has already been explored in [8] , we believe that this work comes to shed more light on this interesting subject, helping to fill in a gap existing in the corres- ponding specialized literature.
2. An Alternative Pathway to Solitons in Sine-Gordon Field Theory
2.1. The Jacobi Amplitude Function
We start by considering the following theory describing a real scalar field in (1 + 1)-dimensions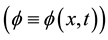 ,
,
 (1)
(1)
where the potential term is given by
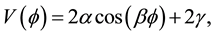 (2)
(2)
with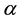 ,
, 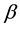 and
and 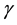 being real parameters.
being real parameters.
The above Lagrangian gives rise, through the Euler-Lagrange equation, 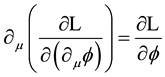 , to the following field equation
, to the following field equation
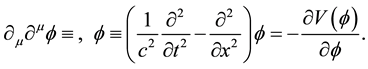 (3)
(3)
Notice that since Equation (3) is invariant under Lorentz transformations 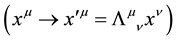 [9] , its solutions may be obtained through the solutions of the corresponding equation for the static case
[9] , its solutions may be obtained through the solutions of the corresponding equation for the static case 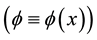 by a simple Lorentz boost, namely
by a simple Lorentz boost, namely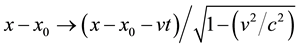 , for arbitrary
, for arbitrary 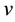
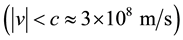 [10] [11] . Thus, in what follows, we will focus on the solutions of the equation
[10] [11] . Thus, in what follows, we will focus on the solutions of the equation
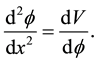 (4)
(4)
Indeed, by multiplying the above equation by 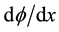 we obtain
we obtain
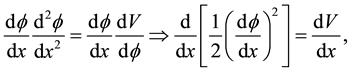 (5)
(5)
which, after an integration with respect to 

By integrating both sides of the above equation, from 




In order to compute the above integral, we must firstly notice that the potential, shown in Equation (2), may be rewritten as

Thus, by making the change of variables




The integral appearing in Equation (9) is called an incomplete elliptic integral of the first kind, 



Notice that, from the above definition, we have
The solution of Equation (4) may be, finally, written as

Hence, from the above equation, we may notice that

as it should.
2.2. The Case
From the definition 



may be obtained as a special case of the solution presented in Equation (11). Indeed, since
where 

Last but not least, we must notice that by substituting the Equation (14) into Equation (3) and making the
change (Lorentz boost)

where 

This result allows us to characterize the Lorentz boosted, and shifted by

as a generalization of the sine-Gordon soliton/anti-soliton solution for
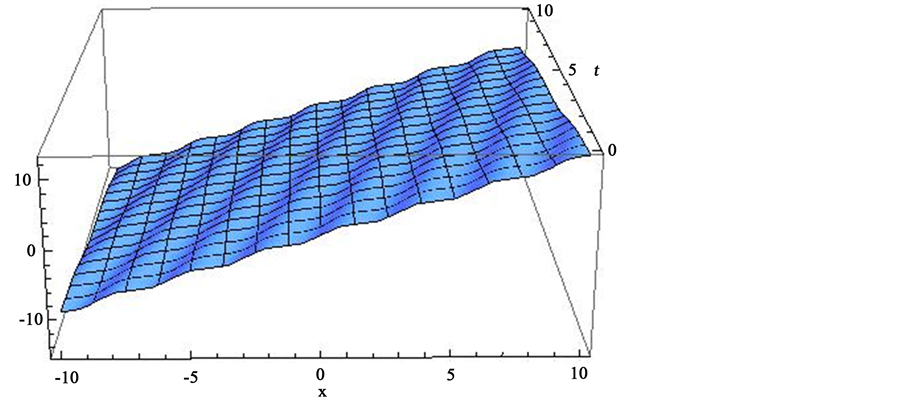
Figure 1. The Jacobi amplitude solution given by Equation (17) with




Figure 2. The soliton solution given by Equation (16) with




3. Concluding Remarks
We would like to make a few comments about the soliton solution, shown in Equation (16), and its generalized version, shown in Equation (17). Firstly, we may notice by comparing Figure 1 and Figure 2 how different are these solutions, where we would like to highlight the doubly periodic behaviour of the Jacobi amplitude solution.
Finally, let us observe that, as remarked in [10] , this soliton solution, though arising in a classical field theory, looks very much like a classical particle since its energy density is localized at a point 


is finite, just as we should expect.
Acknowledgements
This work has been supported by University of Alberta’s Li Ka Shing Applied Virology Institute and CNPq, Conselho Nacional de Desenvolvimento Científico e Tecnológico, Brasil.
References
- Coleman, S. (1975) Quantum Sine-Gordon Equation as the Massive Thirring Model. Physical Review D, 11, 2088- 2097. http://dx.doi.org/10.1103/PhysRevD.11.2088
- Kosterlitz, J.M. (1974) The Critical Properties of the Two-Dimensional XY Model. Journal of Physics C: Solid State Physics, 7, 1046-1060. http://dx.doi.org/10.1088/0022-3719/7/6/005
- Samuel, S. (1978) Grand Partition Function in Field Theory with Applications to Sine-Gordon Field Theory. Physical Review D, 18, 1916-1932. http://dx.doi.org/10.1103/PhysRevD.18.1916
- Dauxois, T. and Peyrard, M. (2006) Physics of Solitons. Cambridge University Press, New York.
- Mondaini, L. and Marino, E.C. (2005) Sine-Gordon/Coulomb Gas Soliton Correlation Functions and an Exact Evaluation of the Kosterlitz-Thouless Critical Exponent. Journal of Statistical Physics, 118, 767-779. http://dx.doi.org/10.1007/s10955-004-8828-y
- Mondaini, L., Marino, E.C. and Schmidt, A.A. (2009) Vanishing Conductivity of Quantum Solitons in Polyacetylene. Journal of Physics A: Mathematical and Theoretical, 42, Article ID: 055401. http://dx.doi.org/10.1088/1751-8113/42/5/055401
- Mondaini, L. (2012) Thermal Soliton Correlation Functions in Theories with a Z(N) Symmetry. Journal of Modern Physics, 3, 1776-1780. http://dx.doi.org/10.4236/jmp.2012.311221
- Cervero, J.M. (1986) Unveiling the Solitons Mistery: The Jacobi Elliptic Functions. American Journal of Physics, 54, 35-38. http://dx.doi.org/10.1119/1.14767
- Mondaini, L. (2012) Obtaining a Closed-Form Representation for the Dual Bosonic Thermal Green Function by Using Methods of Integration on the Complex Plane. Revista Brasileira de Ensino de Física, 34, 3305. http://dx.doi.org/10.1590/S1806-11172012000300005
- Jackiw, R. (1977) Quantum Meaning of Classical Field Theory. Reviews of Modern Physics, 49, 681-706. http://dx.doi.org/10.1103/RevModPhys.49.681
- Rajaraman, R. (1987) Solitons and Instantons: An Introduction to Solitons and Instantons in Quantum Field Theory. Elsevier, Amsterdam.
- Gradshteyn, I.S. and Ryzhik, I.M. (2000) Table of Integrals, Series, and Products. Academic Press, San Diego.
- Weisstein, E.W. Jacobi Amplitude. MathWorld―A Wolfram Web Resource. http://mathworld.wolfram.com/JacobiAmplitude.html