Journal of Applied Mathematics and Physics
Vol.2 No.7(2014), Article
ID:46812,12
pages
DOI:10.4236/jamp.2014.27063
Theory of Dynamic Interactions: The Flight of the Boomerang
Gabriel Barceló
Advanced Dynamics S. A. Madrid, Madrid, Spain
Email: gestor@advanceddynamics.net
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 March 2014; revised 19 April 2014; accepted 28 April 2014
ABSTRACT
We propose a new interpretation of the dynamic behavior of the boomerang and, in general, of the rigid bodies exposed to simultaneous non-coaxial rotations. We have developed a new rotational non-inertial dynamics hypothesis, which can be applied to understand both the flight of the boomerang as well as celestial mechanics. The boomerang is a particularly significant, intriguing and widely known case of bodies in rotation. We have analyzed the velocity and acceleration fields generated when rigid bodies are exposed to successive torques, in order to assess new criteria for this speed coupling. In this context, reactions and inertial fields that cannot be justified by means of classical mechanics take place. Accordingly, we propose a new Theory of Dynamic Interactions. We believe that the results obtained will enable us to conceive a new perspective in dynamics, unknown to date. After carrying out ample research, we have come to the conclusion that there still exists an unstructured scientific area in non-inertial dynamics systems subject to rotational accelerations. The aim of this paper is to present information of the surprising results obtained and to attract interest in research into dynamic field systems accelerated by rotation, and the multiple and remarkable scientific applications arising thereof. We further propose the boomerang as a clear example of the application of the Theory of Dynamic Interactions.
Keywords:Dynamic Systems Theory, Dynamic Fields, Intrinsic Angular Momentum, Speed Coupling, Celestial Mechanics, Boomerang

1. Introduction
The boomerang is an ingenious object known to man for thousands of years. It is so named by a New South Wales (Australia) tribe [1] , however, contrary to what a lot of people may think, it is not an exclusively Australian invention (see audiovisual presentation: https://www.dropbox.com/s/ry4v1gij7jk0upk/Bumerang.mp4).
Traces of these flying objects have been found on all five continents: The ancient Egyptians had a similar weapon, as did the Hopi Indians of Arizona and many other peoples. However, the Maoris are the only people in our times that still use this pre-historic instrument that had been consigned to the past by other peoples, a fact which enabled Captain James Cook to record its existence on arriving at Australian shores in 1770 [2] .
The British Museum in London has an Egyptian tomb on which real life in the marshes is depicted [3] . Hunting in the marshes must have been one of the favorite pastimes of the Egyptian upper class as testified by the illustration in which you can see a hunter using a rabbit stick (figure 1). There are numerous historical references to rabbit sticks and boomerangs.
Therefore, the fact that all cultures, except in Australia, and all peoples, except the Maori people, have left off using this technology at some time in their past, and that its use has only come down to us through the aborigines, is quite amazing.
2. Flying Objects
The boomerang is an instrument that belongs to the group of flying objects that possess the unique and peculiar characteristic that they can return to their point of origin. All of these objects are thrown simultaneously with a rotation at their center of mass; a rotation that remains constant throughout their flight path.
In such circumstances, the common denominator is an inertial reaction of the mass caused by the rotational inertia [2] , which would correspond to the inertia of a body, when subject to an inertial rotational movement on its main axis, by virtue of which it will tend to maintain this rotation, even if the forces acting on it were to cease. This rotational inertia prevents any change to its dynamic state. Under such circumstances it will be possible to identify the property of mass defined as rigidity in space [2] , by virtue of which the body will tend to maintain the existing rotation and, therefore, its dynamic state.
Accordingly, the resulting dynamic state of the flying object will be periodical and stable and may reach a state of dynamic equilibrium [2] . The foregoing can be put down to that property of matter defined as rotational invariance [2] , by means of which, bodies endowed with intrinsic rotation can reach a state of energetic and dynamic equilibrium, apparently immutable and constant owing to their inertial behaviour. The aforementioned rotational invariance is an intrinsic characteristic and independent of any reference system. We can say that any solid in space, if it reaches a state of intrinsic inertial rotational movement on a main axis, will maintain this dynamic state constantly and immutably owing to its rotational invariance, except when impeded from behaving so

Figure 1. Fragment of a marsh hunting scene on the tomb-chapel of Nebamun (British Museum. Detail).
by some other external action.
A simple stick, thrown simultaneously with a rotation at its center of mass, fulfils these characteristics. If the stick in question is curved, its center of mass will not be in the stick itself, consequently its angular momentum will be greater, as will its dynamic stability. Moreover, if the shape of the stick is equivalent that of an aeroplane wing, then it can achieve longer flight duration due to the dynamic effect caused by the lift forces generated. The boomerang possesses all of these characteristics, which are indicative of its historical development from the self-rotating throwing stick to the weapon that returns to its place of origin.
3. Traditional Explanations
A lot of texts claim that the boomerang is as much a glider as it is a gyroscope, but they fail to understand or fully explain the physical phenomena that are generated during its flight. Gliders and paper planes work to overcome air resistance. On their downward flight, both one and the other convert gravity’s potential energy into kinetic energy and, therefore, glide until ending up on the ground. Boomerangs are clearly like aeroplanes and gliders, their arms are wings that experience a lift force when in movement, but the boomerang rotates in the air at the same time, thus its lift force will be perpendicular to its wing, no matter what the latter’s position be [2] .
In our opinion, boomerang dynamics, like that of all flying objects with intrinsic rotation, are not explained by the laws of classical mechanics, but rather form part of the dynamics of non-inertial systems and, more exactly, that of systems accelerated by rotation, in which the moving object is subject, at one and the same time, to numerous non-coaxial rotations.
In the 1970s, Felix Hess carried out an in-depth theoretical and experimental study on the boomerang [4] at the University of Groningen (The Netherlands), which can be taken as the benchmark study in this field (figure 2).
An article was published in the magazine Scientific American [6] by Wolfgang Bürger, also entitled The Flight of the Boomerang in which he carried out a dynamic analysis of this instrument. The author proposed that a boomerang thrown forwards in a vertical position inclines the plane of its blades at the outset and flies in a curve that is approximately on a horizontal plane. According to Hess’s observations we saw that the blade plane is always at a tangent to the flight path.
The rotational momentum of the lift forces of the air is eluded by the boomerang in the same way that a gyroscope does: the plane of its wings rotates at an angular velocity of Ώ = v/(L cos (α)) around the vertical axis that passes through its barycentre… At one and the same time, a rotational momentum acts that wants to tilt the boomerang around the axis of its flight direction; the forward rotating blade experiences a direction wind and a lift force correspondingly greater than the one which is going backwards. As would a gyroscope, the boomerang eludes this rotating momentum by means of a change (precession) of its flight plane. The boomerang returns as a result of the movement in its path and gyroscopic precession [6] .
We find this explanation unsatisfactory. It is a common feature of scientific literature to wish to explain the peculiar flight of the boomerang on the basis of a supposed gyroscopic effect, or as a result of the gyroscopic precession effect. In our opinion these explanations lack a certain precision and do not correspond to a coherent structuring of what is known about dynamics.
In his article, Wolfgang Bürger goes on to acknowledge that there is no definitive, logical answer to explain boomerang behaviour within the realm of classical mechanics.
We do not understand the reason behind this peculiar behaviour being explained by analogical reference to gyroscopes or fictitious inertial forces, as has been the case to date. We believe that these phenomena can be better interpreted within the area of the rotational dynamics of accelerated systems, in accordance with the hypotheses put forward by the Theory of Dynamic Interactions (TDI), which can be consulted on different sites [7] and in several texts [8]. We present our argument below, which is further complemented by an audiovisual presentation.
4. Why Do Boomerangs Not Fall?
On being thrown, the boomerang does not follow the path of any other weighted body that rises while still subject to the thrust of the throwing action and then quickly fall to the ground owing to its weight. It rises at the start of its flight, as can be seen in figure 3, not only because of the impulse received, but also because of another force that makes it rise. The key to this behaviour lies in the peculiar characteristics of its construction, which enable it to glide in the air.
A boomerang must be made of two or more blades, each with an appropriate shape. The blades of a boome-
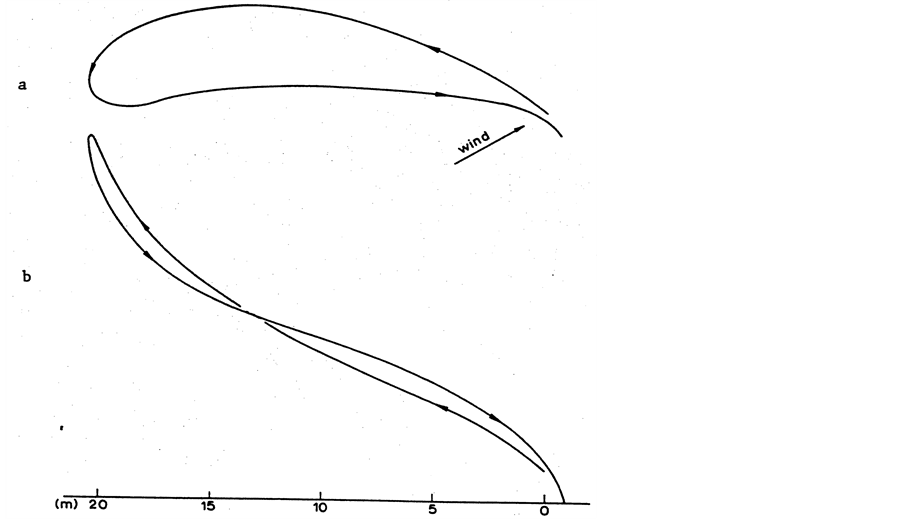
Figure 2. Typical real path of a plywood boomerang according to Hess: a) Bird’s eye view. b) Side view [5] .

Figure 3. Different section views of the boomerang by which one can see how they vary depending on their relative position.
rang are lift surfaces, just like an aeroplane’s wings. Their shape generates a lifting force on moving through the air.
It is precisely the shape of the blades, like the aeroplane’s wings when gliding in the air, that causes the aerodynamic phenomenon that enables their lifting.
By looking at the different boomerang sections, we can see how these vary in accordance with their relative position. The central section is symmetrical, thus it generates a minimum lift in this area. However, along the length of each blade the section is the same as that of a glider wing. Notwithstanding, the section is different and asymmetric on each blade, in keeping with its traslational velocity.
However, in spite of the fact that its flight is prolonged by the lift effect of its blades, the constant braking of the air will reduce its speed, until eventually bringing it to a stop. Whatever the case, its construction characteristics are the key to its peculiar flight and serve to explain its lift, but fail to explain its closed path: the fact that it can return to its origin.
Its characteristic closed path is due to another dynamic phenomenon, which does not occur in bodies thrown without their own rotation, which is why it differs from them: it returns because of its peculiar initial rotation (figure 4) and owing to the new, non-coaxial rotation to which it is subjected.
5. Why Do Boomerangs Return?
We have seen above how, after the initial impulse that projects it and obliges it to turn, the boomerang rises due

Figure 4. Initial boomerang rotation around an external center.
to the aerodynamic lift effect that is generated by its own blades. We stated that, as a force opposing the weight, the lift is generated by the shape of its blades, as occurs with aeroplane wings, and that while it moves through the air, it maintains its rotation on its axis, as can be seen in the figure.
However, we have emphasized how, at the same time, it is being excited by the imbalance of lift and weight forces, on making it rotate on a new axis that is other than the previous one, and which we will call non-coaxial with the initial rotation.
The Theory of Dynamic Interactions (TDI) claims that the boomerang returns to its origin as a result of being a body that is subject to two simultaneous rotations on different axes (figure 5). As of the moment it is first released into the air, in addition to the impulse driving it forward, it is made to revolve around an axis that is perpendicular to its plane.
However, the imbalanced lift force couple and the weight cause a new righting force couple that leads to a new oscillation beginning on a new axis, other than the initial rotation axis.
6. Physico-Mathematical Model
If we analyses the speeds that affect a boomerang’s path that moves its center of mass at a velocity of V (figure 6), and rotates at the same time around a hypothetical axis perpendicular to its plane at a velocity of ω, we will see how each blade moves at a different relative velocity.
After the initial impulse that projects it and obliges it to turn, the boomerang rises due to the aerodynamic lift effect that is generated by its own blades. As a force opposing the weight, the lift is generated by the shape of its blades, as occurs with aeroplane wings. While the boomerang travels through the air it maintains its rotation. If we examine those forces acting on a boomerang with a radius of α, on maintaining a traslational velocity at the same time of V and a rotation velocity of ω, the resulting speed at each blade edge will not be the same: the blade rotating forwards experiences a faster relative wind speed and a correspondingly greater lift force than the blade that is moving backwards [2] .
The blade at the top will have a total velocity of V+ α ω, whereas the blade at the bottom will have a velocity of V− α ω. Given that the blade at the top is moving faster with respect to the air, the greater the lift effect will be at this point: The blade rotating forwards experiences a faster relative wind speed and a correspondingly greater lift force than the blade that is moving backwards [2] .
The different relative velocity of each blade causes an imbalance in the lift forces generated (figure 7), a phenomenon that does not occur in the cases of aeroplanes or gliders. The two blades receive a lift force that causes the boomerang to glide, or even rise, but each blade is driven by different, never equal forces.
Therefore, as the relative velocity of the blades are not equal with respect to the air, and as the lift forces are proportional to their relative velocity, as we have seen, these will be very different for each blade. As a result of the foregoing, we can imagine two imbalanced, lift forces FA and FB, which would oblige the boomerang to rotate on a new axis. figure 7 illustrates the lift forces that are generated on the boomerang blades from a side view, the result and the weight. The imbalance of the lift and weight forces generate a new velocity field (figure 8).
The weight, a force applied at the boomerang’s center of mass, will not coincide with the resultant lift forces, determining a couple that acts at the same time with the rotation, but without being coaxial with it […]. The couple will generate a rotation momentum that tends to tilt the boomerang around its flight direction axis […]. The weight couple and that resulting from the lift forces, which is non-coaxial with the intrinsic rotation of the boomerang, will be the dynamic interaction couple that generates the new path. The boomerang will maintain a

Figure 5. Boomerang rotation axes.

Figure 6. Speeds that affect the path of a boomerang that is moving at a velocity of V and rotating at the same time on a hypothetical axis perpendicular to its plane at a velocity of ω.

Figure 7. A side view illustration of the weight and the lift forces generated on the boomerang.

Figure 8. Velocity field generated by the imbalance of the lift and weight forces.
certain tilt in its flight. This tilt will be maintained throughout its path, given that the generating couple of the dynamic interaction, as happens with all like phenomena, maintains its action but does not cause the body to rotate around its own axis [2] .
It may seem amazing that, in spite of the fact that the lift forces cause this new non-coaxial rotation of the boomerang, and that its own weight further increases this imbalance, the boomerang does not tilt or rotate during flight on account of this new rotation, nor does it appreciably modify the tilt of its plane with respect to the ground.
Moreover, the lift forces are not constant; they fluctuate in accordance with the different air variable, which means that the boomerang will tend to oscillate in the face of the changes caused by them. Notwithstanding, the weight strengthens the torque that will tend to right the boomerang plane. Whatever the case, these forces generate a non-uniform velocity field in the boomerang itself.
In accordance with the Theory of Dynamic Interaction: The anisotropic distribution of the velocities generated by the couple (Vc) shall be compounded with the initial linear velocity (VT), enabling a curved path…
The velocity VR = (vx, vy, vz) of the new path of its centre of mass will be defined by the matrix multiplication of the rotating operator 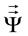 by the velocity vector V0 = (0, V0, 0):
by the velocity vector V0 = (0, V0, 0):
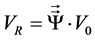 (1)
(1)
As we deduced above, the couple formed by the weight and the lift force acts on the boomerang making it rotate anti-clockwise with respect to X’ (see the previous figure). The matrix operator (figure 9) ![]() will be:
will be:
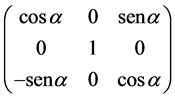
Where the velocity vector ![]() in our reference system:
in our reference system:
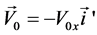
For VR we have:
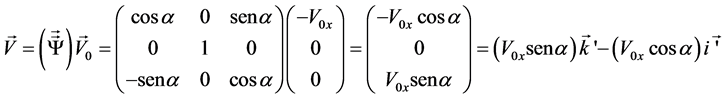
As can be seen, the result of applying the operator is that the velocity of the centre of mass varies its direction by means of a positive or anti-clockwise rotation (figure 10).
This path would be the equivalent of the path that would result from the hypothesis of a generated dynamic interaction couple D, which couples with its linear velocity, determined by the equation:
![]()
And this will be maintained as long as the forces of the momentum formed by the weight and the lift force continue to act.
From:
 ,
, 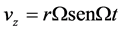
We get:
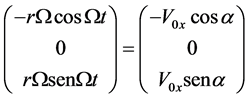
From which we get:
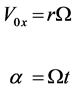
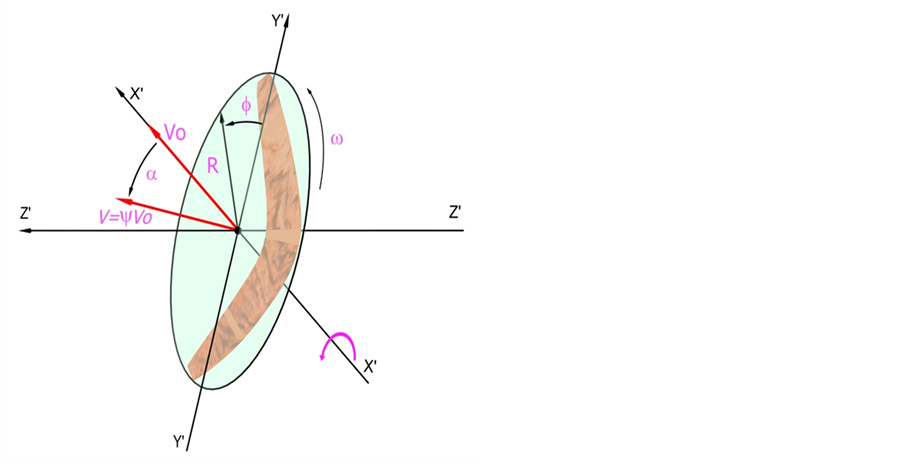
Figure 9. Rotations that generate changes in the boomerang’s path as a result of the coupling of the velocity fields that act on its center of mass.

Figure 10. Theoretical behaviour of the boomerang: Ideal path in the event of not being subject to any motive force.
The value of W is got from resolving![]() , where the path radius is r:
, where the path radius is r:
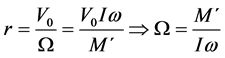
Experiments confirm that the radius of the flight path depends on the launch velocity, and also on the flight velocity and the angular velocity W, thus the boomerang rotates during its flight [2] .
7. The Boomerang Tilt
As we have already indicated, and it is important to keep in mind, a characteristic fact of the flight of the boomerang is that its plane maintains the same tilt throughout its path (figure 11). This is a constant feature in these dynamic phenomena, as was already pointed out by Bohnenberger in the 19th century, on observing the behaviour of the first scientific precursor to the gyroscope [9] . He showed how the rotor always maintained a certain tilt with respect to the vertical, as it followed its precession movement, orbiting, in our case, due to its translational velocity.
This constant tilt of its plane is essential to understanding the dynamics of boomerangs, given that it must even be thrown with a certain tilt, otherwise there will not be enough lift: if it is thrown vertically, it will fall due to a lack of lift force.

Figure 11. Launch angle with respect to the vertical.
Wolfgang Bürger, in the aforementioned article [6] acknowledges that, in accordance with Classical Mechanics, there is no definitive answer to the behaviour of the boomerang and further reiterates that he cannot find any logical explanation for this constant tilt: In spite of his insistence, Hess fails to find a conclusive answer to the question of the origin of the tilt [6] .
Nevertheless, the Theory of Dynamic Interaction does explain how, after being thrown with a certain tilt, the boomerang plane starts to rotate or tilt on the axis coinciding with the translational velocity of its centre of mass, while it begins to travel its known path, maintaining its intrinsic rotation constantly at the same time on another axis, which is perpendicular to the boomerang’s main plane. This is just a further example of the dynamics of bodies subject to two simultaneous non-coaxial rotations, in which the action of the second torque does not generate a new rotation movement of the body, but rather modifies the path of its centre of mass on coupling with the velocity field generated by this new torque with the translational velocity field, which also affects its centre of mass, maintaining the constant tilt of its plane.
8. Experimental Tests
We have conducted several test experiments on the theory under proposal e.g. moving objects with intrinsic rotation on their main axis semi-submerged in water and subject to a righting torque, consisting of the weight and force of floatation, the relative positions of which do not coincide [10] . This righting torque was not coaxial with the intrinsic rotation. The moving object was, therefore, subject to two non-coaxial rotations, as is the case with the boomerang, but we noticed how the rotation caused by the righting torque did not generate any new moving rotations, but rather was transformed into a change of path of the centre of mass [11] . Experiments were also conducted on terra firme [12] , which can also be seen in the video [13] .
It is important to emphasise a particular characteristic of these dynamic phenomena. It happens, for example, in the case of the torque caused by the weight and floatation force, when the centre of gravity and the metacentre do not coincide, which is the case in our experiments with cylinders and the submarine. In these circumstances, as long as there is angular momentum, the newly acting torque does not manage to make the moving object rotate on the axis of this new torque, as this maintains its relative position constant. It seems contradictory that this torque neither acts nor modifies the position of the moving object, which is apparently imbalanced. Only when the moving object stops its intrinsic rotation is it rectified, situating itself in a stable position with respect to its two centres: gravity and the metacentre on the vertical axis itself. Neither inertial nor dynamic reactions are caused in this position of equilibrium.
But this phenomenon, if carefully analysed, also occurs with boomerangs, Frisbees, etc. At least it does so when the speed of rotation of the moving object remains within certain equivalent parameters. In the case of a conservative force field, we could interpret this behaviour on the understanding that when the new torque begins to act, the reaction of the inertial interaction acts at the same time, in such a way that the inertial reaction of the dynamic interaction prevents this rotation from occurring [2] owing to the non-coaxial torque, at least as long as there is intrinsic rotation.
In the light of the foregoing, we can interpret this phenomenon of the constant tilt of the boomerang during its flight as a result of the fact that the effect of the righting torque, due to the weight and imbalance of the lift forces on each blade, generates a velocity field Vc in the boomerang, in such a way that a different speed acts on each point from the contiguous one. That velocity field is, therefore, anisotropic as well as variable in time.
As of that moment, the initial angular displacement caused by the righting torque remains constant, and the boomerang tilts no more, it will simply oscillate if the variables that affect its lift change. Therefore, the boomerang no longer twists. As of that moment (figure 12), the velocity field (Vc) generated by the non-coaxial torque, is added with the translational velocity field (VT), thus generating a resulting velocity field (VR), while the boomerang follows its normal path, with its plane endowed with a constant tilt, returning to its point of origin and maintaining its intrinsic rotation.
This behaviour explains the boomerang’s tilt, as well as the tilt of moving bodies lacking symmetry on three axes when they are subject to dynamic interactions. As stated above, this phenomenon was already observed in the 19th century and has been until now just another paradox in the field of rotational dynamics.
9. Theory of Dynamic Interactions
As has been stated above, the physico-mathematical model developed in the Theory of Dynamic Interactions, which can be applied to non-inertial accelerated systems, has been fully proven by experiment and by computer simulation.
The fact is that the Theory of Dynamic Interactions makes it easy to interpret the flight of the boomerang, though we also hold that this dynamic model is valid to represent any moving object in space with translational velocity, intrinsic rotation and subject to other forces that cause new torques on other, new axes.
It is easy to understand the behaviour of the boomerang, if we accept the true inertial behaviour of bodies in which rotation on an axis of symmetry prevents the compounding of rotations that are not on the same axis. The rotational inertia is such that it prevents any new, non-coaxial rotation being added to the movement of the particles, thus maintaining both rotations without vectorial addition.
The equation for movement that we are proposing in the Theory of Dynamic Interactions for these non-inertial situations is very simple. It is based on the application of an operator ![]() that stands for a rotation in space, in such a way that the end velocity of the boomerang is defined by the matrix multiplication of this operator by the initial translational velocity:
that stands for a rotation in space, in such a way that the end velocity of the boomerang is defined by the matrix multiplication of this operator by the initial translational velocity:
 (1)
(1)
By means of this simple formula it becomes possible to determine the path of the boomerang, or indeed, of any rigid body, in translation when it is simultaneously subject to two rotations on the different axes.
The theory holds that when a rigid body is subject to successive force couples, the first momentum will cause its intrinsic rotation, but the subsequent non-coaxial ones will generate a non-homogenous velocity field, which we can identify as an anisotropic distribution of acceleration which, mathematically speaking, can be conceived of as an inertial force field. If the rigid body also has kinetic translational momentum, a coupling will occur between the translational velocity field and the anisotropic velocity field caused by the second momentum, thus obliging the centre of the moving mass to modify its path, without any external force having been applied in that direction, while maintaining its initial intrinsic rotation constant.
The key to the flight of the boomerang lies, according to its underpinning theory, in the algebraic summing or coupling of the translational velocity fields to the non-homogenous velocity fields created by the weight and the imbalanced lift forces. This coupling of fields, and therefore, this behaviour, will hold as long as the initial rotation of the boomerang lasts.
Furthermore, there will be a transfer of kinetic rotation energy to translation energy, and vice versa, in dynamic phenomena dealt with under this hypothesis.
The mathematical analysis provides us with the theoretical circular path as illustrated in the previous Figure 10, on not including in the formula the initial impulse caused by the throwing force.
It is clear that the real paths are not exactly identical to those of the theoretical model, given that at launch, the boomerang is subject to the impulsive force that is not incorporated into the theoretical model, and moreover, along its path the variables that affect its flight will change, especially the air speed. Accordingly, we can better understand real boomerang paths (figure 2 and figure 13), already observed by Hess [5] and Walker [14] .
The Theory of Dynamic Interactions on which this proposal is based is fully described in different texts and articles, in which it is possible to see how this theory affects, in a far reaching way, the basis principles of dynamics [15] , not to mention astrophysics [16] , cosmology [17] , atomic physics and technology [18] . An analysis

Figure 12. The VT translational velocities are added to the non-homogenous Vc velocities created by the weight and imbalanced lift forces at each point of the boomerang’s mass, thus creating the new VR path.

Figure 13. Typical real boomerang path according to Walker (1897) [14] .
of this theory reveals its capacity to answer numerous unknowns in dynamics and celestial mechanics and, moreover, explains the behaviour of rotating bodies like the boomerang.
The interpretation of the dynamic behaviour of the boomerang, the spinning top, and of host of other rotating objects, based on the re-interpretation of compound movements in accordance with the Theory of Dynamic Interactions can, in our opinion, be generalised to include any free body in space. This way of understanding the movement of rotating bodies can be applied to other free bodies, or ones with support points, in space, whenever these are subject to new non-coaxial rotations [2] .
10. Conclusions
Consequently, we believe that normal questions and answers have been resolved in a scientific manner: Why does the boomerang return? What is the diameter of the return path? What process brakes its flight to the point of detaining it? And why does it always finish with the initial tilt [2] ?
The flight of the boomerang is nothing more than just another example of the dynamics of accelerated systems caused by rotation [19] . The Theory of Dynamic Interactions and its laws of physics [20] generalise the idea of the gyroscopic torque, along with that of other inertial phenomena, bringing them together in a unified structure of a new, non-inertial rotational dynamics. Notwithstanding, this theory, which is simple in structure and easily applicable to, as yet, numerous, unexplained physical phenomena, calls for a new understanding of mechanics, proposing new inertial hypotheses for matter.
Anyone interested in cooperating with this independent research project is invited to ask for additional information from Advanced Dynamics S.A. or check out our site at www.advanceddynamics.net.
References
- Pitt-Rivers (1972) Anthropological and Archaeological Fragments, “Primitive Warfare”. Journal: Royal United Service Inst. xii. No. 51; British Ass. Report (1872); Catalogue of Bethnal Green Collection, p. 28; Buchner in Globus, lxxxviii.39, 63; G. T. Walker in Phil. Trans. cxc.23; Wide World Mag. ii.626; Nature, xiv.248, lxiv.338; Brough Smyth, Aborigines of Victoria, i. 310-329; Roth, Ethnological Studies.
- Barceló, G. (2005) The Flight of the Boomerang. Marcombo, Barcelona. http://www.dinamicafundacion.com/
- British Museum. Tomb of Nebamun. New Egyptian Gallery. http://www.britishmuseum.org/
- Hess, F. (1975) Boomerangs, Aerodynamics and Motion. Groningen University (The Netherlands), Groningen.
- Hess, F. (1968) The Aerodynamics of Boomerangs. Scientific American, 219, 124-136. http://dx.doi.org/10.1038/scientificamerican1168-124
- Bürger, W. (2002) The Flight of the Boomerang. Investigación y Ciencia (Scientific American), No. 304.
- Barceló, G. (2008) A Rotating World. Editorial Marcombo, Barcelona. http://www.dinamicafundacion.com/
- Advanced Dynamics, S.A. http://www.youtube.com/watch?v=P9hGgoL5ZGk&feature=c4-overview-vl&list=PL3E50CF6AEBEED47B
- von Bohnenberger, J. (1817) Tübinger Blütterfür Naturwissenschaft und Arzneikunde.
- Theory of Dynamic Interactions.http://www.youtube.com/watch?v=qK5mW2j2nzU&list=PL3E50CF6AEBEED47B
- Barceló, G. (2011) Analysis of Dynamics Field Systems Accelerated by Rotation. Dynamics of Non-Inertial Systems. De MSET-2011 Congress, Miami. http://www.coiim.es/forocientifico/FORO%20CIENTFICO/Documentos/DeMSET_2011_GBarcelo.pdf
- Pérez, L. (2013) New Evidence on Rotational Dynamics. World Journal of Mechanics, 3, 174-177. http://dx.doi.org/10.4236/wjm.2013.33016
- Pérez, L.A. (2013) Reflecting New Evidence on Rotational Dynamics. http://vimeo.com/68763196
- Walker, G.T. (1897) Philosophical Transactions of the Royal Society of London. Nature, 56, 45-46.
- Barceló, G. (2010) On the Equivalence Principle. 61st International Astronautical Congress, American Institute of Aeronautics and Astronautics, Prague. http://www.coiim.es/forocientifico/FORO%20CIENTFICO/Documentos/ON_THE_EQUIVALENCE_PRINCIPLE.pdf
- Barceló, G. (2013) Proposal of New Criteria for Celestial Mechanics. International Journal of Astronomy and Astrophysics, 3, 385-391. http://dx.doi.org/10.4236/ijaa.2013.34044
- Barceló, G. (2013) Imago Universi: A Story of the Human Conception of the Cosmos. Ed. Arpegio, Barcelona.http://imagouniversi.com/
- Barceló, G. (2013) Technological Applications of the New Theory of Dynamic Interactions. Global Journal of Researches in Engineering: Mechanical and Mechanics Engineering-G, 13.https://globaljournals.org/GJRE_Volume13/E-Journal_GJRE_(G)_Vol_13_Issue_5.pdf
- Barceló, G. (2012) Analysis of Dynamic Fields in Non-inertial Systems. World Journal of Mechanics, 2, 175-180. http://dx.doi.org/10.4236/wjm.2012.23021
- Barceló, G. (2013) Theory of Dynamic Interactions: Laws of Motion. World Journal of Mechanics, 3, 328-338.http://dx.doi.org/10.4236/wjm.2013.39036

