International Journal of Intelligence Science
Vol.2 No.4A(2012), Article ID:24193,9 pages DOI:10.4236/ijis.2012.224024
An Overview of Personal Credit Scoring: Techniques and Future Work
School of Management, Nanjing University, Nanjing, China
Email: lixl@nju.edu.cn
Received May 22, 2012; revised August 23, 2012; accepted September 3, 2012
Keywords: Credit Scoring; Ensemble Learning; Dynamic Behavioral Scoring; Type I and Type II Error
ABSTRACT
Personal credit scoring is the application of financial risk forecasting. It becomes an even important task as financial institutions have been experiencing serious competition and challenges. In this paper, the techniques used for credit scoring are summarized and classified and the new method—ensemble learning model is introduced. This article also discusses some problems in current study. It points out that changing the focus from static credit scoring to dynamic behavioral scoring and maximizing revenue by decreasing the Type I and Type II error are two issues in current study. It also suggested that more complex models cannot always been applied to actual situation. Therefore, how to use the assessment models widely and improve the prediction accuracy is the main task for future research.
1. Introduction
Financial risks continue to spring up in the financial markets during the past decade, which brings huge losses to financial institutions. As a result, financial risk forecasting becomes an even more important task today. Personal credit scoring is an application of financial risk forecasting to consumer lending. It includes credit scoring and behavioral scoring, both of which are the techniques to help organizations decide whether or not to grant credit to consumers who apply to them [1]. Credit scoring determines whether the applicants is qualified while behavioral scoring decides how to deal with existing customers, such as should the firm agree to increase his credit limit or what actions it will take if the customer starts to fall behind in his repayments. In fact, credit scoring is a problem of classification, whose purpose is to make a distinction between “good” and “bad” customers. The banks should extend credit to “good” ones in order to increase the revenue and reject “bad” ones to avoid economic losses.
In 1941, David Durand [2] was the first to recognize ones should differentiate between good or bad loans by measurements of the applicants’ characteristics. After that, credit analysts in financial companies and mail order firms decide to whether to give loans or send merchandise. These rules were summarized and then used by non-experts to help make credit decisions—one of the first examples of expert systems. The arrival of credit cards in the late 1960s made the banks and other credit card issuers begin to employ credit scoring. The usefulness of credit scoring not only improves the forecast accuracy but also decreases default rates by 50% or more. In the 1970s, completely acceptance of credit scoring leads to a significant increase in the number of professional credit scoring analysis. By the 1980s, credit scoring has been applied to personal loans, home loans, small business loans and other fields. In the 1990s, scorecards were introduced to credit scoring.
Up to now, three basic techniques are used for credit granting—expert scoring models, statistical models and artificial intelligence (AI) methods. Expert scoring method was the first approach applied to solve the credit scoring problems. The analysts said yes or no according to the characteristics of the applicants. These credit rating approaches are quite similar. They all make qualitative analysis by scoring the main factors of the credit, such as moral quality, repayment ability and the collateral of the applicants, the purpose and deadline of the loans. However, this method is highly dependent on the experience of experts and their tacit knowledge, which makes it a time-consuming task and brings fatigue and classification error.
In Section II, we will review four kinds of credit scoring methods: statistical methods, artificial intelligence methods, hybrid methods and ensemble methods. Research issues and future problems will be discussed in Section III. Part IV is a conclusion of this paper.
2. Overview of the Techniques
Statistical models and AI models are two most important methods for credit scoring. At present the main research direction has changed from single model into integrated models. So classifying these methods has become a complex and difficult job. In this paper, we sums up these methods and classify them into statistical model, AI model, hybrid methods and ensemble methods.
2.1. Statistical Model@NolistTemp#2.1.1. LDA
LDA (linear discriminate analysis) was first proposed by Fisher [3] as a classification method. LDA uses linear discriminate function (LDF) which passes through the centroids of the two classes to classify the customers. The linear discriminate function is following:
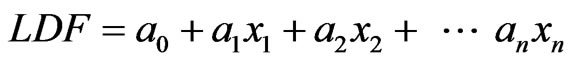 (1)
(1)
where  represents feature variables of the customers and
represents feature variables of the customers and  indicates discrimination coefficients for n variables. LDA is the most widely used statistical methods for credit scoring. However, it has also been criticized for its requirement of linear relationships between dependent variables and independent variables and the assumptions that the input variables must follow Normal distribution. To overcome these drawbacks, Logistic regression, a model which not requires the normal distribution of variables, was introduced.
indicates discrimination coefficients for n variables. LDA is the most widely used statistical methods for credit scoring. However, it has also been criticized for its requirement of linear relationships between dependent variables and independent variables and the assumptions that the input variables must follow Normal distribution. To overcome these drawbacks, Logistic regression, a model which not requires the normal distribution of variables, was introduced.
2.1.2. Logistic Regression
Logistic regression (LR) is a further deformation of linear regression. It has less restriction on hypothesis about the data and can deal with qualitative indicators. LDA analysis whether the user’s characteristic variables are correlation, while Logistic regression has the ability to predict default probability of an applicant and indentify the variables related to his behavior. The regression equation of LR is:
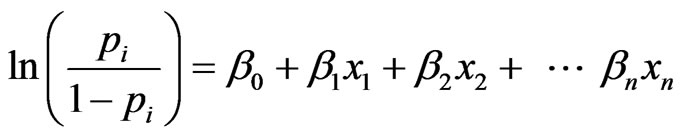 (2)
(2)
The probability 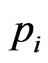 obtained by Equation (2) is a bound of classification. The customer is considered default if it is larger than 0.5 or not default on the contrary. Lin [4] suggested that it is not appropriate to adopt 0.5 as the cutoff point when the number of training samples in two groups is imbalance. He used optimal cutoff point approach and cross-validation to construct a financial distress warning system and get the new cut point 0.314 for classification. LR is proofed as effective and accurate as LDA, but does not require input variable to follow normal distribution.
obtained by Equation (2) is a bound of classification. The customer is considered default if it is larger than 0.5 or not default on the contrary. Lin [4] suggested that it is not appropriate to adopt 0.5 as the cutoff point when the number of training samples in two groups is imbalance. He used optimal cutoff point approach and cross-validation to construct a financial distress warning system and get the new cut point 0.314 for classification. LR is proofed as effective and accurate as LDA, but does not require input variable to follow normal distribution.
2.1.3. MARS
MARS (multivariate adaptive regression splines) is a non-linear and non-parametric regression method first proposed by Friedman [5]. It has strong generalization ability and excels at dealing with high-dimensional data. The optimal MARS model is selected in a two-stage process. In the first stage, a very large number of basis fuctions are constructed to over fit the data, which can be continuous, categorical and ordinal. In the second stage, basis functions are deleted in the order of least contributions using the generalized cross-validation (GCV) criterion. A measure of variable importance can be assessed by observing the decrease in the calculated GCV when a variable is removed from the model. This process will continue until the remaining basis functions all satisfying the pre-determined requirements. The GCV can be expressed as follow
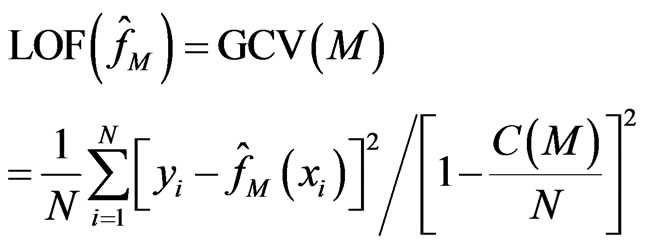 (3)
(3)
where there are N observations, and C(M) is the costpenalty measures of a model containing M basis functions. The numerator indicates the lack of fit on the M basis function model fM (xi) and the denominator denotes the penalty for model complexity C(M). The MARS function is usually represented using the following equation
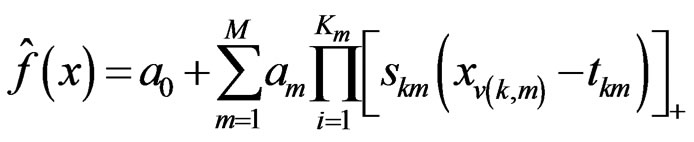 (4)
(4)
where, 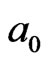 and
and  are parameters,
are parameters, 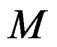 is the number of basis functions,
is the number of basis functions, 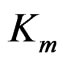 is the number of knots,
is the number of knots,  takes on values of either 1 or –1 and indicates the right/ left sense of the associated step function,
takes on values of either 1 or –1 and indicates the right/ left sense of the associated step function, 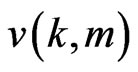 is the label of the independent variable, and
is the label of the independent variable, and 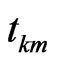 indicates the knot location. Unlike LDA and LR, MARS does not presume that there is a linear relationship between dependent variable and independent variables. In addition, MARS is superior to artificial intelligence methods because of short training time and strong intelligibility. As a result, MARS is usually used as a feature selection technique for classifier in hybrid models in order to obtain the most appropriate input variables.
indicates the knot location. Unlike LDA and LR, MARS does not presume that there is a linear relationship between dependent variable and independent variables. In addition, MARS is superior to artificial intelligence methods because of short training time and strong intelligibility. As a result, MARS is usually used as a feature selection technique for classifier in hybrid models in order to obtain the most appropriate input variables.
2.1.4. Bayesian Model
Bayesian classifiers are statistical classifiers with a “white box” nature. It can predict class membership probabilities, such as the probability that a given sample belongs to a particular class. Bayesian classification is based on Bayesian theory, which is described below. Given the training sample set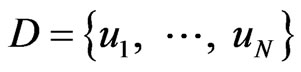 , the task of the classifier is to analyze these training sample set and determine a mapping function
, the task of the classifier is to analyze these training sample set and determine a mapping function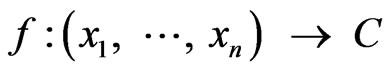 , which can decide the label of unknown ensample
, which can decide the label of unknown ensample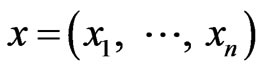 . Bayesian classifiers choose the class which has greatest posteriori probability
. Bayesian classifiers choose the class which has greatest posteriori probability 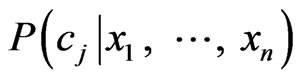 as the label, according to minimum error probability criterion (or maximum posteriori probability criterion). That is, if
as the label, according to minimum error probability criterion (or maximum posteriori probability criterion). That is, if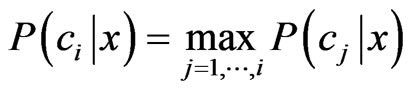 , then we can determine that
, then we can determine that 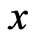 belongs to
belongs to .
.
Naive Bayes and Bayesian belief networks are two commonly used models. Naive Bayesian classifier assumes that the attributions of a sample are independent. Although it simplifies the calculation, the variables may be correlated in reality. Bayesian belief network is a graphical model and allow class conditional independencies to be defined between subsets of variables. Belief network is composed of two parts: a directed acyclic graph and conditional probability tables. Sarkar & Sriram [6] as well as Sun & Shenoy [7] found that Bayesian classifier achieved a high accuracy for prediction.
2.1.5. Decision Tree
Decision tree method is also known as recursive partitioning. It works as follows. First, according to a certain standard, the customer data are divided into limited subsets to make the homogeneity of default risk in the subset higher than original sets. Then the division process continues until the new subsets meet the requirements of the end node. The construction of a decision tree process contains three elements: bifurcation rules, stopping rules and the rules deciding which class the end node belongs to. Bifurcation rules are used to divide new sub sets. Stopping rules determine that the subset is whether or not an end node. C 4.5 and CART are the most two common methods of credit evaluation.
2.1.6. Markov Model
Markov model uses history data to predict the distribution of population in a time point at regular intervals. It speculates the trend of a population based on the regulation of population changing in the past. Liu, Lai & Guu [8] used a hidden Markov model and Fuzzy Markov Model respectively for risk assessment. Wang et al. [9] constructed a Markov network for customer credit evaluation. Frydman & Schuermann [10] presented a mixing Markov model based on two Markov chains for company ratings.
2.2. Artificial Intelligence Methods
LDA and LR are two effective statistic methods. However, Thomas [1] indicated that the classification accuracy of the two models was not very high. With the rapid development of machine learning, more and more Artificial Intelligence methods are applied for credit scoring, such as artificial neural networks (ANN), genetic algorithm (GA) and support vector machine (SVM).
2.2.1. Artificial Neural Networks
ANN is an information processing model resembling connections structure in the synapses. It consists of a large number of nodes (also called neurons or units) by links. The feed-forward neural network with back-propagation (BP) is widely used for credit scoring, where the neurons receive signals from pre-layer and output them to the next layers without feedback. Figure 1 shows a standard structure of a feed-forward network, which includes input layer, hidden layer and output layer. The nodes in input layer receive attributes values of each training sample and transmit the weighted outputs to hidden layer. The weighted outputs of the hidden layer are input to unit making up the output layer, which emits the prediction for given samples.
Back-propagation learns by iteratively processing a set of training samples, comparing the network’s prediction for each sample with the actual known class label. For each training sample, the weights are modified so as to minimize the mean squared error between the network’s prediction and the actual class. The modifications are made in the “backwards” direction, so we name the network back-propagation.
Various activation functions can be applied in hidden layer, such as logistic, sigmoid and RBF. RBF is the most common activation function. It is non-negative and non-linear, a center symmetrical attenuation local distribution function. There are three parameters in RBF: the center, variance and weight of the input units. The weights are obtained by solving a linear equation or using least square method recursion, which makes the learning speed faster and void the problem of local minimum point.
Advantages of neural networks include their strong learning ability and no assumptions about the relationship between input variables. However it also has some drawbacks. A major disadvantage of neural networks lies in their poor understandability. Because of the “black box” nature, it is very difficult for ANN to make knowledge representation. The second problem is how to design and optimize the network topology, which is a very complex experiment process. It is obvious that, the amount of units and layers in hidden layer, different activation function and initial weight values may affect the final classification result. Besides, ANN needs a large number of training samples and long learning time. Abdou, Pointon & Masry [11] found that ANN has a higher accuracy rate by comparing with Logistic regression and discriminate analysis. Desai, Crook & Overstreet [12] made a comparison of neural networks and linear scoring models in the credit union environment and the results indicated that neural network had better performance for correctly classifying bad loans than LR model. Malhotra [13] used fuzzy neural network system (ANFIS) to assess consumers’ loan application and found that fuzzy-neural
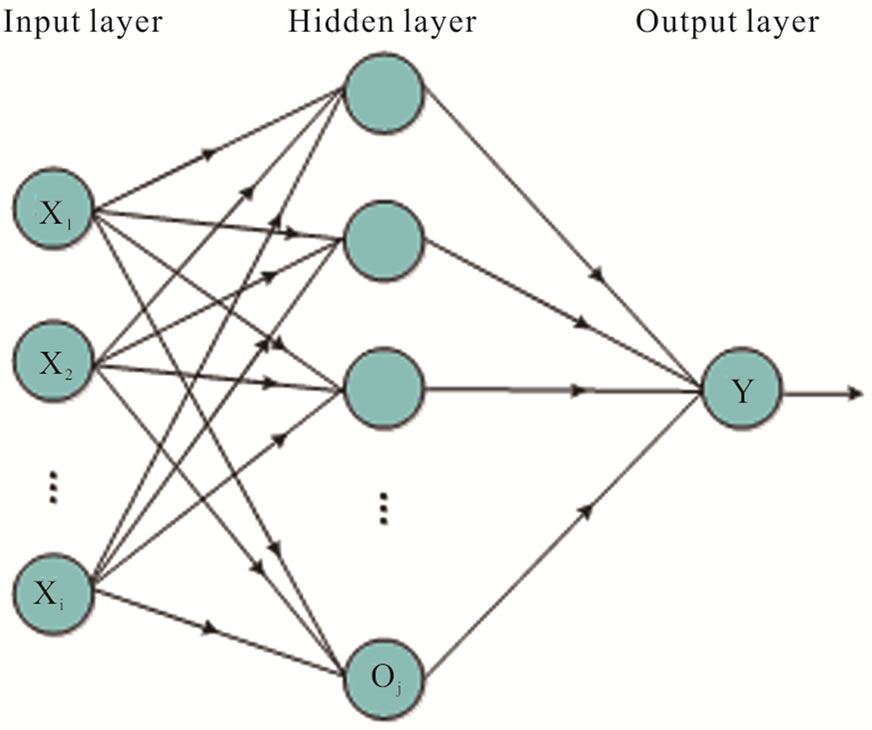
Figure 1. The structure of the neural network.
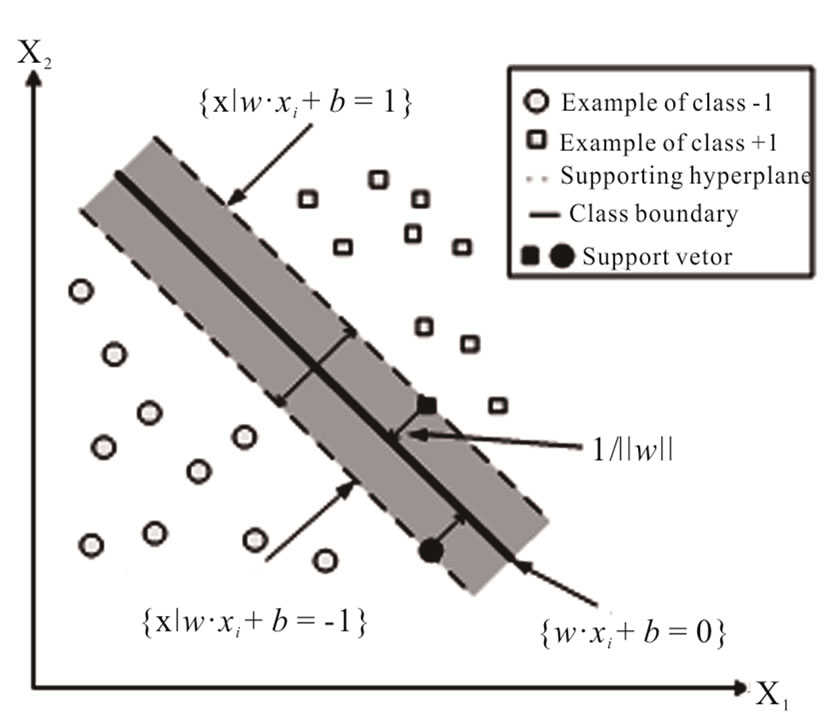
Figure 2. Linear separation of two classes –1 and +1 in twodimensional space.
systems outperformed MDA.
2.2.2. SVM
SVM (support vector machine) is a new AI method for pattern classification which developed in recent years. SVM is suitable for small samples and doesn’t limit the distribution of data. Moreover, it is based on structural risk minimization (SRM) rules which ensure a good robustness theoretically. Figure 2 is an example of SVM.
Let 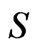 be a dataset with
be a dataset with 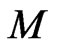 observations:
observations:
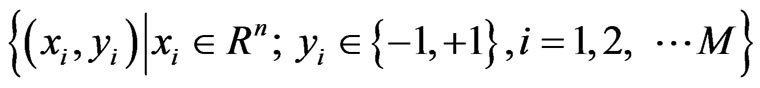 , where xi z
, where xi z 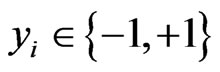 denotes corresponding binary class label, indicating whether the costumer is default. The principle of SVM classification is to find a maximal margin hyperplane to separate examples of opposite labels. The constraint can be formulated as:
denotes corresponding binary class label, indicating whether the costumer is default. The principle of SVM classification is to find a maximal margin hyperplane to separate examples of opposite labels. The constraint can be formulated as:
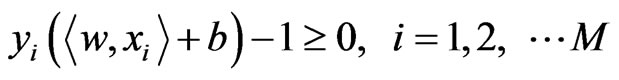 (5)
(5)
where 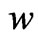 and
and 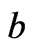 denotes the plane’s normal and intercept respectively.
denotes the plane’s normal and intercept respectively. 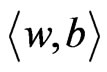 denotes the linear product. The margin of separation is
denotes the linear product. The margin of separation is 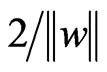 after normalizing the classification equation. The optimal hyperplane is obtained by maximizing the margin
after normalizing the classification equation. The optimal hyperplane is obtained by maximizing the margin , subject to the constraints of Equation (5). Then the classification problem is to solve the following quadratic program;
, subject to the constraints of Equation (5). Then the classification problem is to solve the following quadratic program;
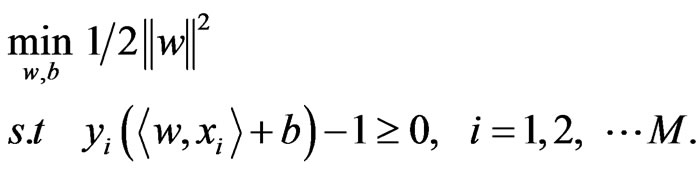 (6)
(6)
By introducing Lagrange multipliers  , the problem is transformed to solving the following dual program :
, the problem is transformed to solving the following dual program :
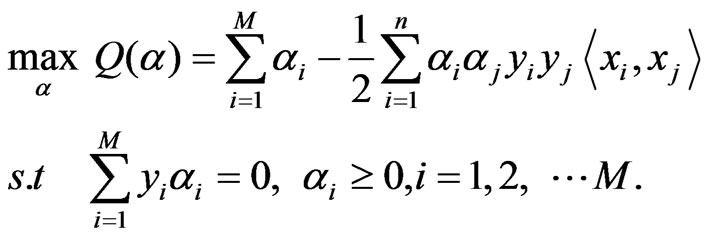 (7)
(7)
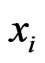 is called support vector if the corresponding
is called support vector if the corresponding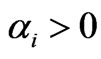 . The decision function obtained by the above problem can be written as:
. The decision function obtained by the above problem can be written as:
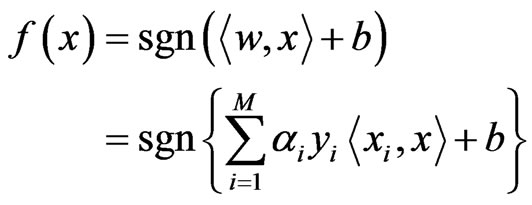 (8)
(8)
The decision function shown above indicates that the SVM classifies examples as class +1 if 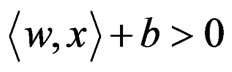 and class –1 if
and class –1 if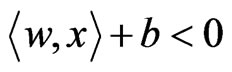 .
.
If the classification problem is linear non-separable, we need to map the input vectors into a high-dimensional feature space via an priori chosen mapping function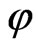 . The mapping can be computed implicitly by means of a kernel function
. The mapping can be computed implicitly by means of a kernel function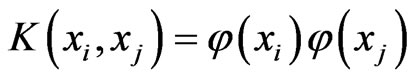 . Linear and polynomial model with degree d, sigmoid and RBF kernel functions are four kinds of kernels. The training errors are allowed in linear non-separable case. The socalled slack variables
. Linear and polynomial model with degree d, sigmoid and RBF kernel functions are four kinds of kernels. The training errors are allowed in linear non-separable case. The socalled slack variables 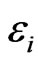 are thus introduced to Equation (5) in order to be tolerant of classification error.
are thus introduced to Equation (5) in order to be tolerant of classification error.
There are many researches on credit scoring using SVM method. Huang, Chen & Hsu [14] pointed out that SVM was superior to ANN in aspect of classification accuracy. Lee (2007) found that SVM was better than MDA, CBR and ANN models. Yang [15] (2007) presented an adaptive scoring system based on SVM, which was adjusted according to an on-line update procedure. Kim & Sohn [16] (2010) provides a SVM model to predict the default of funded SMEs.
2.2.3. Genetic Algorithm and Genetic Programming
Genetic Algorithm (GA) is a computing model which simulates natural selection of Darwinian biological evolution theory and the process of biological evolution in genetic mechanism with the purpose of searching the optimal solution. It was first proposed by professor Hol-

Figure 3. The representation of GP tree.
land [17] from Michigan university of American in 1975.
The main principle of GA can be expressed as follows. According to the evolution theory of “survival of the fittest” and beginning from the initial generation population, some genetic operations including selection, crossover and mutation are applied to screen individuals and generate new populations visa pre-determined fitness function. This process continues until the fitness functions achieve greatest value and obtain final optimal solution. Every population is consisted of several genetically-encoded individuals which are in fact chromosomes.
One of the most important issues of applying GA to credit evaluation is fitness function. A common one can be written as follows:
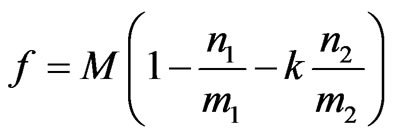 (11)
(11)
where n1 and n2 denote the number of misclassification of two types respectively and m1 and m2 denote the number of samples. n1/m1 and n2/m2 denotes the Type I and Type II classification error. In fact, Type II will bring greater losses so we set a constant k to control it, where k is usually an integer greater than 1. In addition, M is a magnification factor which ensures that the fitness function can change obviously.
Genetic Programming (GP) is developed by Koza [18] (1992). The basic theory of GP is the same as GA. Under GP, each generation of individuals are organized through a dynamic tree structure, which can be expressed as Figure 3: . Individual terminator set and function set are particular parameters in GP. The former includes both input and output variables as a, b, c, x in the figure. While the latter is used to connect leaf nodes to an individual tree, which is a potential solution of a vector. Function sets can include arithmetic operators, mathematical functions, boolean operators, conditional operators and so on. Abdou [19] (2009), and Ong, Huang &
. Individual terminator set and function set are particular parameters in GP. The former includes both input and output variables as a, b, c, x in the figure. While the latter is used to connect leaf nodes to an individual tree, which is a potential solution of a vector. Function sets can include arithmetic operators, mathematical functions, boolean operators, conditional operators and so on. Abdou [19] (2009), and Ong, Huang &
Tzeng [20] (2005) used GP to establish a credit evaluation model.
GA is self-adaptive, global optimal and implicit parallelism. It demonstrates strong robustness and solution skills and can also be able to search global optimization in a complex space. Due to its evolutionary characteristics, GA does not need understand the inherent nature of a problem so that it can handle any form of objective function and constraints, no matter whether they are linear or nonlinear, continuous or discrete.
2.2.4. K-Nearest Neighbor
K-nearest neighbor classifiers are based on learning by analogy. The training samples are described by n-dimensional numeric attributes. Each sample represents a point in an n-dimensional space. When given an unknown sample, a k-nearest neighbor classifier searches the pattern space for the k training samples that are closest to the unknown sample. The distance between two samples is defined in terms of Euclidean distance:
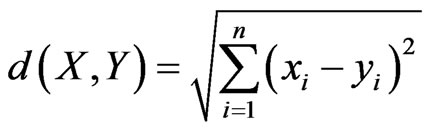 (12)
(12)
The unknown sample is assigned the most common class among its k-nearest neighbors. Arroyo & Maté [21] (2009) combined K-nearest neighbor and time series histogram for forecasting. K-nearest neighbor is in fact a cluster method. Except for K-nearest neighbor, SOM is also a cluster model for credits coring [22]. Luo, Chen & Hsieh [23] built a new classifier called Clustering-launched Classification (CLC) and found it was more effective than SVM.
2.2.5. Case-Based Reasoning
CBR classifiers are instanced-based and store problem resolution of classification. When comes to a new issue, CBR will first check if an identical training case exists. If one is found, then the accompanying solution to that case is returned. If no identical case is found, then CBR will search for training cases that are similar to the new case and find the final solution.
2.3. Hybrid Models
At present, hybrid models that synthesizing advantages of various methods have become hot research topics. However, there is not a clear solution to how to classifying the hybrid models. Generally, the classification is employed according to the different method used in the feature selection and classification stages. Based on this idea, Tsai & Chen [24] (2010) divided them into four types: clustering + classification, classification + classification, clustering + clustering and classification + clustering. He compared four kinds of classification techniques (C 4.5, Naive Bayesian, Logistic regression, ANN) as well as two kinds of clustering methods (K-means, expectation-maximization algorithm EM). The result showed that EM + LR, LR + ANN, EM + EM and LR + EM are the optimal one of the above models respectively. In this paper, we classify hybrid models into simple hybrid and class-wise classifier.
2.3.1. Simple Hybrid Models
In order to illustrate this issue clearly, we divide the process of building a credit evolution model into three steps: feature selection, determination of model parameters and classification. Simple hybrid approach means choosing different methods in these three stages. Feature selection plays an important role. It restricts the number of input features to improve prediction accuracy and reduce the computational complexity. Due to a better robustness and explanatory ability, statistical methods are often used for feature selection. It has been proved that ANN and SVM are the most two effective classifiers therefore both of them are applied in classification stage. Besides, GA and PSO algorithm are used as optimization method to determine model parameters. The simple hybrid modes based on ANN or SVM are listed in Table 1.
ANN classifier always uses statistical methods and GA for feature selection. Šušteršič et al. [26] compared three hybrid models: GA + NN, PCA + NN, LR + NN and found that GA + NN Model is superior to the other two models.
There is anther critic issue, determination of the parameters, for SVM-based hybrid method. RBF is the most widely used in SVM applications. Except for penalty factor C it exhibits one additional kernel parameter γ, which determines the sensitivity of the distance measurement. Other algorithms like GA, grid algorithm and PSO are also used for feature selection and parameter selection. Among them, PSO is a new optimization method developing in recent years, which can not only optimize the parameter in RBF but also control Type II error by choosing an appropriate particle fitness function.

Table 1. Simple hybird methods based on ANN or SVM.
2.3.2. Class-Wise Classifier
There exists anther type of hybrid models: “class-wise” classifier. The information and data collected by credit institutions are often not complete. One solution is to cluster the samples automatically and decide the number of labels before classification stage. That’s why it is called “class-wise” and class-wise classifier is consistent with cluster + classification model proposed by Tsai & Chen [24]. Hsieh & Huang [30] built a clustering-classifier which integrates SVM, ANN and Bayesian network. Hsieh [31] established such a model for credit scoring. He first used SOM clustering algorithm to determine the number of clusters automatically and then used the K-means clustering algorithm to generate clusters of samples belonging to new classes and eliminate the unrepresentative samples from each class. Finally, in the neural network stage, samples with new class labels were used in the design of the credit scoring model.
2.4. Ensemble Classifier
Ensemble learning is a novel machine learning technique. There is no clear definition of ensemble learning. It is generally believed that one of the most important characteristics of ensemble learning is it’s learning for the same problem, which is different from the way obtaining the overall solution from individual solution by solving several sub-problems respectively. The important difference between hybrid methods and ensemble methods is that hybrid methods only use one classifier for sample learning and employ different way in feature selection and classifying stages, while ensemble learning produce various classifier with different types or parameters, such as various SVM classifiers with different parameters, and train different samples for many times .
The principle of ensemble learning model is expressed as following. First, several classifiers are produced and obtain classification results by training them on different samples. Then choose the right classifiers as ensemble members according to certain criterions. Finally, aggregate these ensemble members visa ensemble approach and get the ensemble result. Boosting, stacking and bagging are often used as ensemble approaches. Nowadays, ensemble learning has become the latest method of credit evaluation model. Paleologo, Elisseeff & Antonini [32] proposed a hybrid credit evolution models based on Kmeans, SVM, decision trees and adaboost algorithms and classify the samples by subagging ensemble approach. Yu et al. (2010) [33] employed ANN classifiers with different structures and used maximizing decorrelation to choose the ensemble members. Zhou, Lai & Yu (2010)
[34] built an ensemble model base on least squares SVM. Nanni & Lumini (2009) [35] used random subspace ensemble approach. He found that ensemble classifiers can deal with the issues of missing data and imbalance classes and perform better classification ability and perdition accuracy compared with signal or simple hybrid models.
3. Current Research Issues
Although personal credit evaluation has become a mature research field, there still exist many problems. Building personal credit scoring models faced many challenges in reality, such as half-baked applicant’s information, missing values and inaccurate information. In this section, we will discuss some issues of research problems and future research directions in this field.
3.1. Behavioral Scoring
At present, researchers seldom focus their attention on behavioral scoring. Behavioral scoring makes a decision about credit management based on the repay performance of existing customers during a period of time. Behavioral scoring includes not only basic personal information but also repayment behavior and purchasing history. Therefore, it is a dynamic process which decides whether to increase credibility and refuse or provide extra loans to costumers according to their credit performance. Behavioral scoring is a dynamic process while credit scoring can be reviewed as a static process which deals with only new applicants. Thomas (2000) [1] has introduced a dynamic systems assessment model for behavior scoring, which may become a research trend in future. Hsieh (2004) [36] established a two-stage hybrid model based on SOM and Apriori for behavior management of existing customers in banks. First, SOM was used to classify bank customers into three major profitable groups of customers: revolver users, transactor users and convenience users based on repayment behavior and recency, frequency, monetary behavioral scoring predicators. Then, the resulting groups of customers were profiled by their feature attributes determined using an Apripri association rule inducer.
3.2. Type I and Type II Error
Type I and Type II are two kinds classification error of scoring system. For banks, Type I error classify good customer as bad one and reject their loans, which will reduce banks’ profit. In contrast, Type II error classify bad customer as good one and provide loans, which will bring loss to banks. The researches focus more on Type II error because it is generally believed that it may bring about more serious damage to credit institutions. In addition, Type II error is also a criterion to evaluate a credit model. SVM is considered having an advantage over ANN because that its fitness function has the ability to control Type II. However, it should not been ignored that reducing Type I can also cause an increase in revenue. Chuang and Lin (2009) [37] presented a reassigning credit scoring model (RCSM) in order to decrease Type I error. First they used ANN to classify applicants as accepted good or rejected bad credits. Then the CBR-based classification technique was used to reduce Type I error by reassigning the rejected good credit applicants to conditional accepted class and provide a certain amount of loans to them. In short, how to decrease losses and at the same time maximize the revenues is a major research direction in future work.
3.3. The More Complex a Model, the Better the Classifier?
The number of credit scoring models becomes larger and each one has its own advantages. Although multi-model hybrid method and ensemble learning models is the research trend, credit score is still the widespread way to decide whether grant credit to applicants or not. The issues of application and promotion of these credit scoring models may face challenges in the future. Angelini (2008) [38] pointed out that future work should focus on models’ generalization capability and applicability. On one hand, hybrid and ensemble models which integrate advantages of different methods obviously perform higher classification accuracy. However, whether classification accuracy should be the only evolution criterion is still doubtful. On the other hand, new models are getting more complex and difficult, while the implementation cost of these models becomes much higher. Credit scoring cards and logistic regression are still the widely-used methods for credit scoring.
3.4. Incorporate Economic Conditions into Credit Scoring?
Credit scoring belongs to financial activity. In the financial area, it is impossible that all the situations are as the same as what people have predicted. Forecasting also has its limitation [39]: (1) chaotic limitations. It means that our present knowledge is limited and may not correct; (2) stochastic limitations. It means that the random situation is unpredictable and this compels us to take economic condition into account when taking part in financial activities. In short, economic condition has an effect on the evolution criterion of credit institutions. When economic condition is in depression, it is suggested that evolution criteria should be properly lenient to increase the revenue of credit institutions.
4. Conclusion
This paper gives an overview of credit scoring and sums up various techniques used for credit risk evolution. It credit scoring methods into statics models, AI models, hybrid methods and ensemble methods. Ensembled learning has been widely applied to personal credit evolution and has better classification ability and prediction accuracy. At last, several main issues in the process of building models have been discussed in this paper. In a conclusion, the widespread application and improvement in predication accuracy is the research trends in this field.
REFERENCES
- L. C. Thomas, “A Survey of Credit and Behavioral Scoring: Forecasting Financial Risk of Lending to Consumers,” International Journal of Forecasting, Vol. 16, No. 2, 2000, pp. 149-172. doi:10.1016/S0169-2070(00)00034-0
- D. Durand, “Risk Elements in Consumer Instatement Financing,” National Bureau of Economic Research, New York, 1941.
- R. A. Fisher, “The Use of Multiple Measurements in Taxonomic Problems,” Annuals of Eugenices, Vol. 2, No. 7, 1936, pp. 179-188.
- S. L. Lin, “A New Two-Stage Hybrid Approach of Credit Risk in Banking Industry,” Expert Systems with Applications, Vol. 36, No. 4, 2009, pp. 8333-8341. doi:10.1016/j.eswa.2008.10.015
- J. H. Friedman, “Multivariate Adaptive Regression Splines,” Annals of Statistics, Vol. 19, No. 1, 1991, pp. 1-141. doi:10.1214/aos/1176347963
- S. Sarkar and R. S. Sriram, “Bayesian Models for Early Warning of Bank Failures,” Management Science, Vol. 47, No. 11, 2001, pp. 1457-1475. doi:10.1287/mnsc.47.11.1457.10253
- L. Sun and P. P. Shenoy, “Using Bayesian Networks for Bankruptcy Prediction: Some Methodological Issues,” European Journal of Operational Research, Vol. 180, No. 2, 2007, pp. 738-753. doi:10.1016/j.ejor.2006.04.019
- K. Liu, K. K. Lai and S.-M. Guu, “Dynamic Credit Scoring on Consumer Behavior Using Fuzzy Markov Model,” 2009 Fourth International Multi-Conference on Computing in the Global Information Technology, Cannes, August 2009, pp. 235-239.
- S. C. Wang, C. P. Leng and P. Q. Zhang, “Conditional Markov Network Hybrid Classifiers Using on Client Credit Scoring,” 2008 International Symposium on Computer Science and Computational Technology, Shanghai, December 2008, pp. 549-553. doi:10.1109/ISCSCT.2008.337
- H. Frydman and T. Schuermann, “Credit Rating Dynamics and Markov Mixture Models,” Journal of Banking & Finance, Vol. 32, No. 6, 2008, pp. 1062-1074. doi:10.1016/j.jbankfin.2007.09.013
- H. Abdou, J. Pointon and A. E. Masry, “Neural Nets Versus Conventional Techniques in Credit Scoring in Egyptian Banking,” Expert Systems with Applications, Vol. 35, No. 2, 2008, pp. 1275-1292. doi:10.1016/j.eswa.2007.08.030
- V. S. Desai, J. N. Crook and G. A. Overstreet, “A Comparison of Neural Networks and Linear Scoring Models in the Credit Union Environment,” European Journal of Operational Research, Vol. 95, No. 1, 1996, pp. 24-47. doi:10.1016/0377-2217(95)00246-4
- R. Malhotra and D. K. Malhotra, “Differentiating between Good Credits and Bad Credits Using Neuro-Fuzzy Systems,” European Journal of Operational Research, Vol. 136, No. 1, 2002, pp. 190-211. doi:10.1016/S0377-2217(01)00052-2
- Z. Huang, H. Chen, C. J. Hsu, W. H. Chen and S. Wu, “Credit Rating Analysis with Support Vector Machines and Neural Networks: A Market Comparative Study,” Decision Support System, Vol. 37, No. 4, 2004, pp. 543-558. doi:10.1016/S0167-9236(03)00086-1
- Y. X. Yang, “Adaptive Credit Scoring with Kernel Learning Methods,” European Journal of Operational Research, Vol. 183, No. 3, 2007, pp. 1521-1536. doi:10.1016/j.ejor.2006.10.066
- H. S. Kim and S. Y. Sohn, “Support Vector Machines for Default Prediction of SMEs Based on Technology Credit,” European Journal of Operational Research, Vol. 201, No. 3, 2010, pp. 838-846. doi:10.1016/j.ejor.2009.03.036
- J. Holland, “Genetic Algorithms,” Scientific American, Vol. 267, No. 1, 1992, pp. 66-72. doi:10.1038/scientificamerican0792-66
- J. R. Koza, “Genetic Programming on the Programming of Computers by Means of Natural Selection,” The MIT Press, Cambridge, 1992.
- H. A. Abdou, “Genetic Programming for Credit Scoring: The Case of Egyptian Public Sector Banks,” Expert Systems with Applications, Vol. 36, No. 9, 2009, pp. 11402- 11417. doi:10.1016/j.eswa.2009.01.076
- C. S. Ong, J. J. Huang and G. H. Tzengb, “Building Credit Scoring Models Using Genetic Programming,” Expert Systems with Applications, Vol. 29, No. 1, 2005, pp. 41-47. doi:10.1016/j.eswa.2005.01.003
- J. Arroyo and C. Maté, “Forecasting Histogram Time Series with K-Nearest Neighbours Methods,” International Journal of Forecasting, Vol. 25, No. 1, 2009, pp. 192-207. doi:10.1016/j.ijforecast.2008.07.003
- J. T. S. Quah and M. Sriganesh, “Real-Time Credit Card Fraud Detection Using Computational Intelligence,” Expert Systems with Applications, Vol. 35, No. 4, 2008, pp. 1721-1732. doi:10.1016/j.eswa.2007.08.093
- S. T. Luo, B. W. Cheng and C. H. Hsieh, “Prediction Model Building with Clustering-Launched Classification and Support Vector Machines in Credit Scoring,” Expert Systems with Application, Vol. 36, No. 4, 2009, pp. 7562-7566. doi:10.1016/j.eswa.2008.09.028
- C. F. Tsai and M. L. Chen, “Credit Rating by Hybrid Machine Learning Techniques,” Applied Soft Computing, Vol. 10, No. 2, 2010, pp. 374-380. doi:10.1016/j.asoc.2009.08.003
- T. S. Lee and I. F. Chen, “A Two-Stage Hybrid Credit Scoring Model Using Artificial Neural Networks and Multivariate Adaptive Regression Splines,” Expert Systems with Application, Vol. 28, No. 4, 2005, pp. 743-752. doi:10.1016/j.eswa.2004.12.031
- M. Šušteršic, D. Mramor and J. Zupan, “Consumer Credit Scoring Models with Limited Data,” Expert Systems with Applications, Vol. 36, No. 3, 2009, pp. 4736-4744. doi:10.1016/j.eswa.2008.06.016
- C. L. Huang, M. C. Chen and C. J. Wang, “Credit Scoring with a Data Mining Approach Based on Support Vector Machines,” Expert Systems with Application, Vol. 33, No. 4, 2007, pp. 847-856. doi:10.1016/j.eswa.2006.07.007
- W. M. Chen, C. Q. Ma and L. Ma, “Mining the Customer Credit Using Hybrid Support Vector Machine Technique,” Expert Systems with Applications, Vol. 36, No. 4, 2009, pp. 7611-7616. doi:10.1016/j.eswa.2008.09.054
- P. Yao, “Hybrid Classifier Using Neighborhood Rough Set and SVM for Credit Scoring,” 2009 International Conference on Business Intelligence and Financial Engineering, Beijing, July 2009, pp. 138-142. doi:10.1109/BIFE.2009.41
- N. C. Hsieh and L. P. Hung, “A Data Driven Ensemble Classifier for Credit Scoring Analysis,” Expert Systems with Application, Vol. 37, No. 1, 2010, pp. 534-545. doi:10.1016/j.eswa.2009.05.059
- N. C. Hsieh, “Hybrid Mining Approach in the Design of Credit Scoring Models,” Expert Systems with Application, Vol. 28, No. 4, 2005, pp. 655-665. doi:10.1016/j.eswa.2004.12.022
- G. Paleologo, A. Elisseeff and G. Antonini, “Subagging for Credit Scoring Models,” European Journal of Operational Research, Vol. 201, No. 1, 2010, pp. 490-499. doi:10.1016/j.ejor.2009.03.008
- L. Yu, S. Y. Wang and K. K. Lai, “Credit Risk Assessment with a Multistage Neural Network Ensemble Learning Approach,” Expert Systems with Application, Vol. 34, No. 2, 2008, pp. 1434-1444. doi:10.1016/j.eswa.2007.01.009
- L. Zhoua, K. K. Laia and L. Yub, “Least Squares Support Vector Machines Ensemble Models for Credit Scoring,” Expert Systems with Applications, Vol. 37, No. 1, 2010, pp. 127-133. doi:10.1016/j.eswa.2009.05.024
- L. Nanni and A. Lumini, “An Expermental Comparison of Ensemble of Classifiers of Bankruptcy Prediction and Credit Scoring,” Expert Systems with Applications, Vol. 36, No. 2, 2009, pp. 3028-3033. doi:10.1016/j.eswa.2008.01.018
- N. C. Hsieh, “An Integrated Data Mining and Behavioral Scoring Model for Analyzing Bank Customers,” Expert Systems with Applications, Vol. 27, No. 4, 2004, pp. 623- 633. doi:10.1016/j.eswa.2004.06.007
- C. L. Chuang and R. H. Lin, “Constructing a Reassigning Credit Scoring Model,” Expert Systems with Application, Vol. 36, No. 3, 2009, pp. 1685-1694.
- E. Angelini, G. D. Tollo and A. Roli, “A Neural Network Approach for Credit Risk Evaluation,” The Quarterly Review of Economics and Finance, Vol. 48, No. 4, 2008, pp. 733-755. doi:10.1016/j.qref.2007.04.001
- D. J. Hand, “Mining the Past to Determine the Future: Problems and Possibilities,” International Journal of Forecasting, Vol. 25, No. 3, 2009, pp. 441-451. doi:10.1016/j.ijforecast.2008.09.004

