Open Journal of Philosophy
Vol.06 No.01(2016), Article ID:63620,17 pages
10.4236/ojpp.2016.61009
Why Interpret Quantum Physics?
Edward MacKinnon
Philosophy Department (Emeritus), California State University East Bay, Hayward, CA, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 December 2015; accepted 19 February 2016; published 22 February 2016
ABSTRACT
This article probes the question of what interpretations of quantum mechanics actually accomplish. In other domains, which are briefly considered, interpretations serve to make alien systematizations intelligible to us. This often involves clarifying the status of their implicit ontology. A survey of interpretations of non-relativistic quantum mechanics supports the evaluation that these interpretations make a contribution to philosophy, but not to physics. Interpretations of quantum field theory are polarized by the divergence between the Lagrangian field theory, which leads to the Standard Model of Particle physics and the Algebraic quantum field theory that discounts an ontology of particles. Ruetsche’s interpretation offers a potential for loosening the sharp polarization that presently obtains. A brief evaluation focuses on the functional ontology of quantum field theory considered as an effective theory.
Keywords:
Interpretation, Quantum Mechanics, Quantum Field Theory, Ontology

1. Introduction
Interpreting quantum mechanics has flourished as a cottage industry among philosophers of science and some philosophically inclined physicists. Physicists regularly ignore, and sometimes ridicule, such attempts. This gap between interpretation and practice raises reflective questions. What does an interpretation add to the item interpreted? What standards are there for judging the success of an interpretation? A brief consideration of other areas where interpretation makes a recognized contribution can supply a preliminary guide. To parallel the problems, we will focus on interpretations of organized, however loosely, systems of knowledge rather than the interpretation of particular items such as Hamlet or the Mona Lisa.
According to hermeneuticists, there is no reading of a text, following of a practice, or adherence to a tradition without an interpretation. To clarify this dictum, we need an initial distinction between an implicit, or functional, interpretation and an explicit, or external, interpretation. A child reading an adventure story does not regard herself as interpreting anything. Her mother may make this functional interpretation explicit by pointing out which features are real and which are make believe.
The implicit/explicit distinction becomes more significant when we consider the efforts of anthropologists. Bronislaw Malinowski pioneered the practice of observer participancy. He learned the language of the Trobriand islanders, participated in their activities, and conformed to their customs ( Malinowski, 1953 [1921]). He examined the peculiar practice of gift giving, the Kula ring. The giving away Soulava, a red shell necklace, was always travelled by boat in a clockwise direction. The recipient of the necklace eventually travelled further in the same direction and passed on the gift. Those giving away Mwali, white shell bracelets, repeated the practice but travelled in a counter-clockwise direction. Malinowski claimed that the natives had no understanding of the total outline or function of the practice. From his outside perspective as an interpreter, Malinowski could explain how this evolved practice facilitated trade and promoted social coherence.
The analysis of totemism illustrates the anthropological interpretation of conceptual structures abstracted from practice. Totemism, found in almost all primitive societies, generally involves three elements: an organization of a tribe into clans, attribution of particular animals, or occasionally plants, to individual clans; and stories detailing how primitive ancestors establish a special relation with the clan’s totemic figure. Claude Levi-Strauss presented a structural explanation ( Lévi-Strauss 1963 ). Primitive people are like us in trying to understand their world through a conceptual ordering. Lacking an abstract logic, they rely on adapting two conceptual structures embedded in their normal practice, kinship structures and their classification of animals and plants. If I am a fox and you are an eagle then we are in different clans and can recognize established relations concerning marriage alliances, superiority, and the assignment of tasks. Members of the clan use these conceptual structures. An anthropologist, functioning as a participant observer, can abstract conceptual structures from normal practice and interpret their organizing role.
An insider who questions an established practice may assume the role of an interpreter. Suppose that the only linguistic means primitive Greeks have for reporting thunder and lightening is to say “Zeus roared”. Then a sceptic came to doubt the existence of the sky gods. Confronted with thunder, he could only report it by claiming: “Zeus roared [but Zeus does not exist]”. This functional contradiction compels an attempt at developing an interpretation that resolves or mitigates the clash.
This way of relying on the functional role of gods and goddesses while bracketing the question of their real existence is illustrated on a sophisticated level in the plays of Euripides1. Euripides’s plays, like those of Aeschylus and Sophocles, rely on the traditional mythology. Yet, Euripides seems to have become a sceptic about the truth of this mythology. However, instead of discarding it, he used it as a vehicle for communicating ideas and emotions. Segal explains how these myths came to comprise a vast system of verbal, visual, and religious symbols, a second-order semiotic system embodying a network of logical relations operating through specific narratives. Here, we have interpretation functioning on two levels. Euripides relies on a functional interpretation of a mythological tradition. Segal explains what Euripides has accomplished by interpreting Euripides’s reliance on mythology as a second-order semiotic system. This is close to the final stage in the process of replacing mthopoetic by rational thought.
This method of interpreting native ontological commitments as conceptual structures that play a functional role extends to other fields. Scholars treating the Gospels as historical texts were puzzled by the nativity accounts found in Matthew and Luke. These accounts were written about seventy to ninety years after the event treated, were not based on eyewitness reports, and featured such extraordinary details as a star hovering over a particular location, choirs of angels, wise men from afar bringing symbolic nativity gifts, and the family’s flight to and return from Egypt to avoid Herod’s massacre of the infants. These accounts also clash with other historical accounts that relate Herod’s notorious misdeeds but make no mention of a slaughter of infants.
Scholars noted that these nativity accounts have the form of a midrash aggadah. A midrash was something Jewish scholars developed to fill in gaps in scripture. An Aggadah form filled the gaps by telling stories. The nativity accounts were written around the time when the doctrine of Jesus’s divinity was developing ( Crossan, 1991 ). They contributed to this development not only by attributing Jesus’s conception to divine intervention but also by presenting Jesus as the fulfilment of prophetic traditions. Though Jesus was probably born in Nazareth, the nativity accounts place his birth in Bethlehem, the city of David. He is presented as recapitulating the defining event in Jewish history by fleeing to and returning from Egypt.
This reinterpretation makes the Nativity accounts intelligible to critics who do not accept the religious beliefs the accounts presuppose. Yet, this still leaves a puzzling feature. How could the early believers accept the claim that a star guided the Magi and finally hovered over a particular habitation? (Matthew 2, 9) To make this intelligible we have to replace our stellar ontology by a more primitive ontology. If stars are small lights not far from the earth’s surface that occasionally flash across the sky as shooting stars, then the idea of a particular star having a much slower and more controlled trajectory becomes intelligible, even though we find it unacceptable.
These examples illustrate different functions an interpretation may accomplish. Internally it might dissolve, or resolve, puzzling or incoherent features of accepted accounts or practices. Why do people shake hands when they meet, wear neck ties or veils, and consider certain foods tabu? The types of external interpretations we have considered try to make a contribution by interpreting systems of knowledge from the perspective of a superior systematization. This need not imply that our culture is superior to the others considered. But, for example, our knowledge of astronomy is superior to the primitive view that stars are little bright lights close to the earth that occasionally streak across the sky. Interpretation from a superior perspective clarifies the account by explaining the functional role of the primitive astronomy.
Here a note on terminology is in order. We will use “metaphysics” for philosophical theories of ultimate reality, such as the metaphysics of Aristotle, Leibniz, or Whitehead. Ontology will be used in a Quinean sense referring to what is accepted as the furniture of the world. Functional ontology is usually implicit in presuppositions governing meaningful discourse. In the examples considered interpretation from a superior perspective untangled a mixture of epistemological and ontological considerations. Interpreting totemism as a tool for systematizing basic knowledge enables us to achieve an understanding of primitive social customs without accepting the reality of totemic figures. Dropping the gods and goddesses presiding over human affairs enables us to understand Greek plays as dramatizations of problematic human situations.
Something similar happens in physics when original interpretations of a theory are replaced by interpretations based on further developments of a theory. This can be illustrated by two examples. Newton thought that a full scientific explanation should involve three steps: mathematics, physics, and philosophy2. Books 1 and 2 of the Principia supply a mathematical analysis of the consequences of different force laws and an application of Newtonian laws to idealized bodies. Book 3, the physics component, applies this mathematics to the “System of the World”. The philosophy should be an explanation through causes. Newton thought that a causal account should rely on God as first mover and controlling power, and the invariant properties of hard indestructible atoms as the ultimate intrinsic source of the phenomena treated in the Principia3. However, the mathematics of the Principia did not rely on either God or atoms. The different causal hypotheses that Newton developed were not published, presumably because Newton found them unsatisfactory. In the next fifty years Newtonians gradually dispensed with the idea that mechanics needs an ontological foundation and treated mechanics itself as a foundation for any account of matter and its properties4. When mechanics was interpreted as foundational then the world was understood as a deterministic mechanistic system. The development of relativity and quantum mechanics led to a reinterpretation of classical mechanics as an effective theory for treating interactions involving relatively low energies and limited velocities. As such, it cannot supply a fundamental ontology.
Maxwell also believed that an adequate scientific theory should be based on an explanation through causes. He realized that the set of equations he had developed did not meet these standards. In 1865 he resigned his chair at King’s college and retired to the family estate of Glenair, where he spent most of his time attempting to develop a satisfactory theory of electrodynamics. In 1873 he published his Treatise ( Maxwell, 1954 [1873]). Here he frankly admitted that he did not know: what electricity is (p. 35); or the direction and velocity of current (p. 570). His earlier ethereal account involved stress in the medium. However, he did not know how stress originates (p. 644), or what light really is (p. 821). He recognized his theory as a phenomenological, rather than a depth, account (p. 574).
Heinrich Hertz’s experiments confirmed Maxwell’s account of the propagation of electromagnetic vibrations. Yet, after a detailed study of Maxwell’s Treatise Hertz concluded that he did not know what Maxwell’s theory is. Hence, he suggested “Maxwell’s theory is Maxwell’s set of equations” ( Hertz, 1962 [1892], p. 21). This reinterpretation changed the significance accorded the electrical charge and displacement. The specific dielectric capacity, ε, and the specific magnetic capacity, μ, were reinterpreted as characterizing properties of material bodies rather than, as Maxwell thought, the medium. When a depth account was finally developed in the theory of electroweak interactions it relied on a foundation, gauge invariance, which neither Maxwell nor Hertz anticipated. The reinterpretation of electrodynamics as a gauge theory coupled to an account of light in terms of photons accorded electrodynamics the status of an effective theory. An effective theory is regarded as valid within a limited energy range but replaceable by a more basic theory for higher energies5.
Can philosophy supply a superior perspective for the interpretation of scientific theories? In times past some philosophers thought that an established metaphysical system, such as Thomism or Marxism, could supply a secure foundation. Supporters of such positions are now a small and shrinking enclave within philosophy. Yet, many philosophers believe that philosophy can supply a superior perspective for treating metascientific issues. Philosophers have a long tradition of analyzing conceptual systems, the structure and interpretation of theories, the role of empirical evidence, methods of confirmation and falsification, and basic issues in ontology and epistemology. Any presumption that philosophy is superior to physics, no matter what form it takes, is an abiding source of friction between physicists and philosophers. A rejection of this presupposition justifies physicists neglect of philosophical interpretations. We will focus on the issue of how this allegedly superior perspective might untangle the ontological and epistemological threads woven together in the tapestry of quantum mechanics.
2. Non-Relativistic Quantum Mechanics
My purpose here is one of probing what interpretations of non-relativistic quantum mechanics (NRQM) have accomplished, but not of adding to the long list of interpretations developed in the last ninety years. We consider the basic features of NRQM to be features of QM as such. This will be followed by a briefer consideration of Quantum Field Theory (QFT). We will limit our consideration to standard quantum mechanics6. To make this more specific we need some preliminary distinctions. Implicit in the normal practice of quantum physics is a functional interpretation of the physics practised, something physicists absorb through training and assimilation. A brief historical summary indicates how this developed.
The atomic physics community experienced a deep crisis in the period from 1922 to 1927. The Bohr-Som- merfeld atomic theory was recognized as inadequate. Wave-particle duality became problematic for electrons as well as photons. The Bohr-Kramers-Slater (B-K-S) treatment of radiation supported predictions that were experimentally falsified. De Broglie, Heisenberg, and Schrödinger developed new breakthroughs which initially seemed incompatible. To achieve a functional coherence some interpretative problems had to be resolved7. We will indicate three problems where interpretation played a decisive role. The first was the relation between classical and quantum physics. The new emerging quantum physics was treated as an extension of classical physics. Bohr’s (forward) Correspondence Principle used classical formulations as a basis for guessing quantum formulations. The Bohr-Sommerfeld atomic model coupled classical accounts of orbits with non-classical accounts of orbital transitions. Heisenberg and Pauli began to insist on a reliance on observables rather than models. A second problem was the non-classical double valuedness that Pauli introduced. Both Pauli and Heisenberg initially rejected the interpretation of this in terms of electron spin. The spin interpretation became acceptable when Bohr showed that the angular momentum of an isolated electron was not measurable. A final problem was dispersion theory. The B-K-S paper interpreted this through the virtual oscillator model. When this was rejected a new interpretation had to be worked out.
To clarify the developing functional interpretation of the new quantum physics we will use Niels Bohr as participant observer, a choice that requires some justification. We will focus on Bohr’s efforts in the mid 1920s to restore coherence to the discourse of physics and postpone discussion of the Copenhagen interpretation. We begin with his treatment of wave-particle duality. This was commonly treated as an ontological problem. How can an electron have both wave and particle properties? Bohr treated this as a linguistic, or conceptual, problem. His account of complementarity specified the type of experimental contexts in which either the conceptual cluster centring on “particle” or the complementary cluster centring on “wave” could be used. This notion of complementarity was extended to the relation between classical and quantum physics. Bohr interpreted the new quantum mechanics as the only rational generalization of classical physics compatible with the quantum of action. His analysis entered on the conditions for the unambiguous communication of experimental information. He treated the mathematical formalism as an inferential tool. He presented no ontology of the quantum domain. His guidelines on the use and restriction of classical terms in quantum contexts became normative even among physicists who did not understand or accept Bohr’s interpretation of quantum physics8. Bohr had consistently rejected Einstein’s light-quantum hypothesis. He accepted Dirac’s formulation of quantum electrodynamics as allowing an acceptable interpretation of photons, the term that came to replace light-quantum.
Bohr’s conceptual analysis resolved the problem of incoherence in scientific discourse and contributed to the development of a functional interpretation of the new quantum physics. The significance of Bohr’s semantic restrictions can be seen can be seen by its application to Bell’s theorem. Bell’s original formulation was: “Consider a pair of spin one-half particles formed somehow in the singlet state and moving freely in opposite directions.” ( Bell, 1964: p. 195 ). This and other formulations of Bell’s theorem rely on the classical concept of particles moving in separate trajectories and postulates that they are combined in a singlet quantum state. Classical particles do not conceptually support quantum states. A singlet quantum state is a holistic system that does not allow precise specification of components. The fact that all formulations of Bell’s theorem violate Bohrian semantics is not a sufficient reason to prohibit testing. However, the test results are summarized in the plaintive claim: Bohr wins again.
Subsequent developments so distorted the general perception of Bohr’s position that it is now difficult to realize the significance of his linguistic orientation. What became accepted as “The Copenhagen Interpretation” was an interpretation of the mathematical formalism that features two types of processes: a causal development in accord with Schrödinger’s equation and a reduction of the wave packet in measurements. Then Bohr’s scattered accounts are interpreted as a comment on this interpretation. Bohr never held this Copenhagen interpretation. He consistently treated the mathematical formalism as an inferential tool, not as a theory to be interpreted. He never invoked a reduction of the wave packet, or a projection postulate, to explain measurement. For Bohr an experiment, or measurement, meant a procedure whose results could be communicated in unambiguous language9.
After the 1927 Solvay conference and the publication of Heisenberg’s uncertainty principle a general consensus emerged, which we can take as the functional interpretation of quantum physics. It includes: Heisenberg’s uncertainty principle; the idea that photons, electrons, and other particles exhibit both wave and particle properties; the probabilistic interpretation of the wave function; the correspondence between eigenvalues derived from the mathematical formalism and values of quantities obtained from measurements; the idea that wave and matrix mechanics are special representations of a more general formalism; some sort of complementary relation between classical and quantum physics; and the backward Correspondence principle that quantum mechanics merges with classical mechanics in the limits of large quantum numbers or in contexts where terms multiplied by h are negligible. Some aspects were left open to interpretation, e.g. whether the y-function should be interpreted as representing a superposition of states or be given a statistical interpretation. In 1927 most of these features seemed novel and more than a bit bizarre. By 1929, they were generally accepted as part of the normal practice of quantum physics. Though Bohr’s restrictions on the use of classical concepts was assimilated into scientific discourse, his underdeveloped doctrines that classical concepts stemming from ordinary language play a definitive role in measurement, and that quantum physics is a rational generalization of classical physics were widely regarded as speculative philosophical issues.
2.1. Orthodox Quantum Mechanics
For Bohr and for the physicists using quantum mechanics to solve outstanding problems the mathematical formalism was treated as a tool, not as a theory to be interpreted. We will use “orthodox quantum mechanics” for interpretations based on the mathematical formalism. Dirac, and independently Jordan, developed a transformation theory relating wave and matrix formulations of QM. John von Neumann insisted that a new formulation was needed because the Dirac formulation in no way satisfied the requirements of mathematical rigor. (von Neumann, p. x). He developed a Hilbert space formulation where the state of a system is represented by a wave function and quantities by hypermaximal (aka self-adjoint) operators. He accommodated the functional interpretation by excluding hidden variables and limiting allowed values of observables to eigenvalues given by the theory. Since his (or Wigner’s10) treatment of the measurement problem played a major role in subsequent interpretation a summary is in order.
The key assumption, distinguishing it from Bohr’s treatment, is that both the object measured and the measuring apparatus are treated as quantum systems. In Bohr’s perspective this may treat measurement qua process but not measurement qua measurement Von Neumann assumed that the measurement interaction couples the object and the apparatus together in a pure state. The dynamics of Schrödinger’s equation is unitary leading from pure states only to other pure states. A pure state for a coupled system does not allow unique values for the systems coupled. A measurement yielding unique values for a pointer reading is interpreted as implying that this was the value the observable possessed prior to measurement. To fit this into the formalism von Neumann introduced a postulate that projects a superposition of states into a mixture with probability coefficients for different values. Von Neumann’s formulation supplies the point of departure for the orthodox interpretation of quantum mechanics.
2.2. Interpreting Non-Relativistic Quantum Mechanics
Quantum mechanics has been a subject for interpretation for over eighty years. My purpose here is not to add a further interpretation, but to consider what these interpretations have accomplished. Obviously some severe restrictions are needed. First, I will focus on works by philosopher that took the mathematical formalism of Non-relativistic Quantum Mechanics (NRQM) as a basis for interpreting the essential features of quantum physics. Next we will consider two works that consider the practice of quantum physics, rather than the mathematical formalism, as the foundation for an interpretation. Quantum field theory will receive a separate section. The selection of authors treated may seem, and probably is, arbitrary. I can only consider works I am familiar with.
Philosophical interpretations of QM were conditioned by ideals of what an explanatory theory should be. The dominant position, stemming from a tradition stretching from Aristotle and Euclid through David Hilbert, regarded theories as axiomatic systems. This facilitated interpretation since the truth of a theory hinged on the truth of its axioms. Many textbooks on QM feature axioms or postulates. But these were organizing principles rather than axioms in Hilbert’s use of the term. Stricter axiomatic formulations either had limited scope ( Mackey, 1963 ) or proved inadequate. We will take Scheibe’s treatise ( Scheibe 1973 ) as the most carefully developed interpretation of QM in the axiomatic tradition.
Scheibe’s clearly stated goal is to defend the orthodox interpretation of QM. He does this by focusing on a critical reconstruction of its logical structure. An abstract representation of the logical structure accorded objects and properties in classical mechanics, classical statistical mechanics, and quantum mechanics supplies a basis for clarifying similarities and differences. Scheibe distinguishes an ontic interpretation, concerning the state of an individual object; an epistemic interpretation, concerning states of knowledge; and a statistical interpretation, concerning relative frequencies in an ensemble. In QM the state of an object prior to measurement has only a blurred reality. The measurement does not supply an adequate basis for predicting future values. Accordingly, the ontic interpretation of the state of an object must be supplemented by either an epistemic or a statistical interpretation. With these restrictions the logical structure of QM in the orthodox interpretation is judged to be complete and consistent. Altmanspacher and Primas (2002) have updated Scheibe’s formulation. The ontic interpretation refers to an isolated system independent of empirical access. An epistemic state presupposes an interaction with an apparatus and is always contextual. However, on a higher level, e.g. atomic physics, chemistry, one may speak of relative onticity or, in present terminology, a functional ontology.
Though Scheibe’s austere formulation is remote from the normal practice of QM, it does not significantly differ from the functional interpretation implicit in normal practice. By the 1980s various factors altered the problematic of interpreting QM. The various tests of Bell’s theorem supported orthodoxy over the theorem’s predictions. Bell’s criticism of von Neumann’s argument against hidden variables stimulated an interest in heterodox interpretations. The orthodox interpretation did little to dissipate the strangeness QM manifested in such phenomena as the single slit double slit experiment, entanglement, distant correlation, and the acausal nature of the measurement problem. The axiomatic, or syntactical, mode of interpreting theories was eclipsed by semantic methods that interpreted a formalism through a family of models, at least one of which is taken to be a model of some aspect of reality. The growing rejection of logical positivism led to a renewed interest in ontological foundations and in the problematic of scientific realism. In this environment the interpretation of QM emerged as a growth industry.
The three basic problems that concerned interpreters were the completeness and consistency of QM and its ontological significance. The problem of completeness centered on the possibility of completing the orthodox interpretation by including hidden variables. Claims of inconsistency focused on the problem of including the measurement process within the formalism. To narrow this issue we will only consider attempts to treat this within a more or less standard formulation of QM. This rules out other types of solutions: approximate solutions, such as the stochastic spreading of superposition over such large numbers of degrees of freedom characterizing the apparatus that interference effects become negligible ( Daneri et al., 1962 ); idealized solutions that treat the apparatus as an infinite collection of quantum systems ( Bub, 1988 ; Robinson, 1994 ); psychologistic solutions that appeal to psycho-physical parallelism (von Neumann 1955; London & Bauer, 1939 ; Wigner, 1967 , chaps 12, 13); the funny way mental states supervene on quantum states ( Albert, 1992 ); or a generalized quantum mechanics that tolerates fuzzy measurements ( Busch, Grabowski, & Lahti, 1995 ).
We will briefly consider some influential interpretations of NRQM, focusing on what the interpretations sought to accomplish. Jeffrey Bub ( Bub, 1974 ) took as his goal an explanation of how quantum mechanics relates to it predecessors. To do this he interpreted both classical and quantum mechanics as principle theories, or theories that introduce abstract structural constraints that events should satisfy. Each can be represented by an abstract mathematical structure. The phase-space structure of classical mechanics is isomorphic to a Boolean algebra, while the Hilbert-space structure of QM is isomorphic to a partial Boolean algebra. Applied to measurement situations this means that any particular measurement can be represented by a Boolean structure, in which every proposition is either true or false. However, separate measurement situations are included in a larger structure, a partial Boolean algebra. In this structure not every proposition has a truth value. This can support the interpretation that QM is incomplete. It does not incorporate the values some observables may possess. Bub’s suggestion is that the only way to remedy this incompleteness is to develop an alternative theory, such as the the Bohm-Bub hidden variables interpretation.
The next interpretations we will consider treat the problem of realism and rely on modal interpretations. The various forms of quantum realism share a common core, the insistence that unmeasured observables possess some sort of values. This has an initial plausibility. If an experimenter had decided to measure momentum, rather than position, she would have found a value. Discussions stemming from Gleason’s theorem, the Kochen- Specker refutation of hidden variables and especially the experimental refutation of Bell’s theorem have led to widespread acceptance of constraints that any realistic, or hidden-variable, interpretation must meet. These constraints rule out: an ignorance interpretation, allowing unmeasured observables to have sharp though unknown values; any local hidden-variable interpretation; or any classical common-cause solution of Einstein-Podolsky- Rosen type coincidences. So the trick is to assign values to some observables without violating these constraints or introducing inconsistencies.
Modal interpretations were stimulated by
Kochen
’s (
1985
) biorthonormal decomposition theorem. Diecks extended this into an interpretation of QM as a theory about properties, or values of physical magnitudes (
Diecks, 1986
). Consider a system, 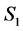 represented by a Hilbert space,
represented by a Hilbert space,  , and system
, and system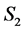 , represented by
, represented by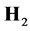 , joined to form a larger system, represented by
, joined to form a larger system, represented by , in a pure state,
, in a pure state,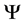 . By using the Schmidt orthogonalization procedure one can get the decomposition,
. By using the Schmidt orthogonalization procedure one can get the decomposition,  , where
, where 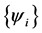 is an orthonormal basis for
is an orthonormal basis for ,
, 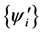 is an orthonormal basis for
is an orthonormal basis for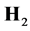 , and degeneracies have been neglected. This is a theorem about Hilbert space, not quantum measurements. A naive measurement interpretation identifies
, and degeneracies have been neglected. This is a theorem about Hilbert space, not quantum measurements. A naive measurement interpretation identifies 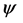 with an object system,
with an object system, 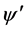 with an apparatus and the summation as correlating definite states of the object with pointer readings. In this interpretation even unobserved states have values. This simple interpretation, however, is prohibited by the orthodox interpretation which allows definite values only to the overall state,
with an apparatus and the summation as correlating definite states of the object with pointer readings. In this interpretation even unobserved states have values. This simple interpretation, however, is prohibited by the orthodox interpretation which allows definite values only to the overall state,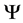 . Modal interpretations drop the orthodox eigenstate-eigenvalue correlation and have various ways of applying the biorthonomal decomposition to quantum measurements.
. Modal interpretations drop the orthodox eigenstate-eigenvalue correlation and have various ways of applying the biorthonomal decomposition to quantum measurements.
Subsequently, three books by Hughes (1989) , Healey (1989, 1991) , and Van Fraassen (1991) accept a modal interpretation of QM and treat measurement as a basic consistency problem. All assume that measurements require state preparation, that the combined object + apparatus is represented by a pure state in a tensor-product Hilbert space and that a deterministic evolution of this state leads to pure states only for the coupled systems, not for the object or the apparatus considered separately. Hughes relies on a minimal extension of Hilbert space that allows an answer to what he calls “Feynman’s forbidden question”: What must the world be like if quantum mechanics is true of it? After considering and criticizing other solutions Hughes advocates relinquishing the Aristotelian categorial system of objects with properties and interprets one version of quantum logic, based on the algebra of subspaces, as a logic of events. This goes beyond the Copenhagen interpretation by including relations between incompatible observables. Then Hughes can retain the projection postulate, and thus the possibility of unique measurement outcomes, by giving the postulate an epistemological interpretation as a conditionalization of the quantum-mechanical state due to increased information.
What is distinctive about Healey’s development is that it is unabashedly metaphysical. He makes two basic assumptions. The first is that quantum systems have physically real dynamical states, something different from quantum states, that allow a specification of values for some dynamical properties. The second is that quantum systems form hierarchies of systems of systems in which wholes can have properties not reducible to properties of subsystems. The biorthonormal theorem is applied to an idealized measurement interaction that correlates the final state of the measuring apparatus with the initial state of a variable characterizing the object. The quantum state is assumed to be supervenient on both the dynamical state and the apparatus. The quantum state can be established retrospectively. Healey rejects the projection postulate and explains the discontinuity involved in measurement partially through a change from the perspective of state preparation to the perspective of measured results, and partially to an uncontrollable interaction with the environment. The quantum state is constrained so that it yields Born’s rule. This can supply an explanation of quantum coincidences if one attributes to objects non-classical holistic properties.
Van Fraassen’s magisterial tome is not just an interpretation of quantum mechanics. It is an attempt to reconstruct quantum mechanics in accord with his version of constructive empiricism. In this view theories are acceptable because they are empirically adequate, not because they are thought to be true. The justification for this claim hinges on the idea that phenomena underdetermine the theories that fit them and theories underdetermine the interpretations that seek to explain them. Interpretations are superfluous. They have no empirical content. All interpretations of QM are hidden variable interpretations. Nevertheless, the construction of a model of what the world would be like if QM were true of it deepens our understanding of quantum mechanics. He develops two models: a geometrical model of the theory and a surface model of the data. By invoking superselection rules and reductionism he is able to develop a treatment of measurement without either a projection postulate or an appeal to epistemological conditionalizing of knowledge. A rejection of the eigenvector-eigenvalue correlation leads to his Copenhagen variation of the modal interpretation. Observables can have values that the dynamic state does not generate. However, the only values that can be considered true are those that the dynamic state makes true.
2.3. Variant Interpretations
To round out this survey we will consider two interpretations that focus more on the semantic and linguistic issues that Bohr raised than on the mathematical formalism. These are in effect interpretations of the practice of physics. The first is developed by Michel Bitbol (1996, 1998, 2002, 2007) . From his very detailed analysis, we will siphon off the philosophical perspective in which his interpretation is embedded. Both analytic philosophy and the natural perspective of Husserl’s phenomenology accept the common sense conceptualization of reality as a point of departure. Drawing on both Husserl and Quine, Bitbol regards predication as stemming from a subjective selection and stabilization of perceived properties. This generates the basic subject/object distinction with the object as the bearer or properties and the subject as the generator of anticipations structuring perceptions. Extension of this framework along Kantian lines involves focusing on a priori forms and the processing of scientific experiments. Bitbol accepts Bohr’s guidelines on the contextual interpretation of experiments and of the mathematical formalism as a contextual predictive mechanism.
This epistemological orientation supports reflective metaphysics, centering on knowledge of objects rather than a metaphysics of objects. In the natural standpoint material objects are basic because they have the characteristics of stability and law-like behavior. In a quantum context state vectors have these properties. When Bohr’s semantic analysis is put in this perspective then wave-particle complementarity is recognized as a principle regulating the extension of classical concepts to quantum situations. The standard measurement problem presupposes that “state a system” has ontological significance apart from the conditions of measurement. Reflective metaphysics dissolves this presupposition as well as the Bell non-locality problem. The dissolution hinges on a recognition that in quantum contexts the preconditions of knowledge are also the preconditions of the empirical content of knowledge.
Edward MacKinnon ’s interpretation ( 2011 ) begins with a neo-Kantian epistemology. Roughly speaking neo- Kantian epistemology differs from Kantian in its treatment of categories, or foundational concepts. Where Kant bases categories on a psychological analysis and justifies their necessity by a transcendental deduction, neo- Kantians ground categories in linguistic usage along the lines developed by Wilfrid Sellars. The novel feature of this approach is a detailed examination of the way ordinary language is extended to and restricted in quantum contexts.
This leads to the idea of a dual-inference system. The extended ordinary language used to describe experimental situations and report results can supply a systematization of Bohrian semantics. Thus, in contexts where the classical concept “particle” is applicable one can rely on the material inferences the concept entails. The Bohrian idea of the mathematical formalism as an inference mechanism leads to a measurement interpretation of quantum mechanics. Adapting work by Dirac and Schwinger’ algebra of measurements an analysis of quantum measurement preparations generates a state-space representation of NRQM. This is extended to QFT through Schwinger’s assumption that the introduction of dynamical field variables can be used to give a sub-microscopic descriptive account anchored in the space-time framework of the measuring apparatus.
MacKinnon argued that this minimal interpretation is functionally adequate for NRQM and quantum electrodynamics, but not for advances in QFT, or the standard model of particle physics, or to quantum cosmology. His treatment of these advances undercuts attempts to derive or impose a fundamental ontology from an analysis of theories. The prediction of new particles, such as the W and Z bosons, quarks, the Higgs particle, and the yet to be discovered axions and super symmetric particles relied on general principles particularly symmetry, conservation, and gauge invariance. The functional theories that incorporate these principles should be regarded as effective theories with functional ontologies proper to particular ranges of interaction energies. An analysis of such functional ontology should include virtual interactions and virtual particles. MacKinnon, accordingly, advocates a reliance on a Consistent Histories formulation. This is presented as something downwardly compatible with Bohrian semantics, and capable of accommodating quantum field theory and quantum cosmology.
3. Quantum Field Theory
Relativistic quantum field theory presents an interpretative problem significantly different from the interpretation of NRQM. There an orthodox interpretation with variant forms is largely consistent with the practice of physics and can supply a basis for different interpretations. QFT admits of three types of formulations. The Lagrangian formulation (LQFT) supplies the theoretical basis for the standard model of particle physics. Yet purists find it appalling. It has three parts covering strong, electromagnetic, and weak interactions that are simply glued together. It does not admit of a single Hilbert space formulation. It relies on series expansions that do not converge and on a particle notion that many find incompatible with a proper formulation of QFT. Yet, in its scope and precision it is the most successful theory in the history of physics. It is capable in principle of handling all the known interactions of quarks, leptons, fermions, photons, and W and Z bosons11.
Algebraic and the associated axiomatic formulations (AQFT) treat observables rather than states as foundational. Quantization of classical fields lead to commutation and anticommutation relations and a C* algebra of local observables12. States are defined as linear functionals on the algebra of observables. The Gelfand-Naimark- Segal construction leads from an algebra of observables, 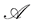 , to a Hilbert space,
, to a Hilbert space, 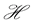
Finally, there is the path integral method stemming from Feynman’s formulation of QM. This is not a theory but a method of calculation based on intuition and ad hoc rules. In this formulation all interactions are treated as particle exchanges. Interpretations of QFT systematically avoid this. However, it is a basic tool used in the advancement of QFT and generates the most perplexing ontological problems. What is one to make of virtual particles and the vacuum that generates them. Interpretations depend on the formulation of QFT chosen. Here we will limit our considerations to the ontological status accorded fields and particles.
The initial issue is the reality of quantum fields. Schwinger, who dominated the earlier development of LQFT thought that the to-be-developed theory should treat “particle” as a phenomenological concept and accord a foundational role to operator fields. These specify the momentum-energy density at a point. He thought that this concept was a step beyond Bohr’s Correspondence principle and brought quantum mechanics to full maturity ( Schwinger, 1983: p. 343 ). This reliance was methodological, rather than ontological. He systematically avoided ontological issues13.
Paul Teller does treat the ontology of QFT ( Teller, 1995 ). In place of an ontology of particles or fields he introduces a new notion, quanta. Roughly speaking quanta can have particle properties without a supporting substance, a sharp spatio-temporal location, or the individuality characterized by a primitive thisness. His development can accommodate a Fock-space representation of field theory for non-interacting quanta. This promising notion remains underdeveloped. Teller’s account treats the QFT that functioned before the introduction of gauge fields and the standard model.
Others attempt to develop an analytic (or functioning) ontology of QFT by introducing new ontological concepts, such as fact ontologies, occurrent ontologies, trope ontologies, and fractured ontologies ( Simon, 2002 ; Seibt, 2002 ). There is a general problem faced by any introduction of novel ontological concepts. If the new terminology is to be something more than a rechristening of old concepts then the new concepts must function as parts of a coherent conceptual system. The innovators are aware of this problem. Yet, their efforts to develop a novel adequate conceptualization are, at best, preliminary.
Sunny Auyang puts the interpretation of QFT in a Kantian perspective. “Object, property, quantity, and relation are general concepts that constitute the categorial framework within which the substantive concepts are acknowledged as descriptive of the world.” ( Auyang, 1995: p. 12 ). This is presented as an account of the a priori role of the Aristotelian categorization schema in ordinary knowledge. In her account scientific theories introduce new substantive concepts, but rely on the same categorial framework. The extension of this general framework to QFT admits of two realizations: one based on entities; the other based on conjunction of qualities.
The ontology of individual entities relies on three general concepts: numerical identity; possibility; and kind. In the specification of fields by 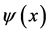
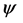
Laura Ruetsche ’s Interpreting Quantum Thories ( 2002 ) should become an indispensable text for philosophers interested in QFT. It manifests a mastery of the mathematics used in AQFT and of the philosophical issues involved in the interpretation of QFT. It presupposes a high level of familiarity with QM, AQFT, physics, and abstract mathematics. She favors interpreting theories as they function in different contexts rather than a pristine interpretation of general theories. An interpretation, in her view, should clarify the explanatory capacity of a theory. Any quantum theory requires a state space, a set of observables, and a dynamics, all of which are partially interpreted. A philosophical interpretation should go beyond this by identifying possible worlds in which the theories propositions are true. However, fulfilling this requirement would not prove that a theory is true simpliciter.
The particular theory she focuses on is labelled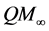
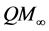
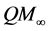
She develops her own interpretation by contrast with two extremes. The Hilbert Space Conservative holds that only one Hilbert space representation is correct. The Algebraic Imperialist insists on interpreting only the algebra of observables. She counters the Conservative by arguing that their the unique choice is not adequately justified, and the Imperialist with the contention that the abstract formulation is incapable of handling some particular explanations. This double rejection renders theory interpretation a more sprawling procedure based on both the algebra of bounded observables and Hilbert space representations, and that interpretations vary from context to context. This, she argues, undercuts the “no miracles” argument that the success of a theory is a sufficient warrant for accepting it as true. Truth, like success, takes different forms in different contexts.
On ontological issues Ruetsche admits that the particle notion is used to interpret high energy experiments and is also used in the standard model of particle physics. However, she argues, the phenomenological concept “particle” proper to experiments is not a part of fundamental physics. The theoretical concept “particle”, grounded in creation operators, allows for inconsistent uses. The particle concept that functions in the initial and final states of S-matrix theory differs from the particle concept proper to interactions. Such considerations, supplemented by Haag’s theorem, leads to the conclusion that QFT is not based on an ontology of particles. One might object that her analysis centers on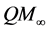
AQFT has never countenanced a particle ontology ( Halvorson & Clifton, 2002 ). The standard model’s reliance on particles is judged to have a status similar to its reliance on sloppy math. The path integral method would be based on a particle ontology, had Feynman not prohibited seeking depth accounts ( Feynman et al., 1963: Vol. 3, p. 11 ). What might these contradictory evaluations allow as an ontology of QFT? I conclude with my own evaluation.
4. Evaluation
Our earlier considerations suggest that interpretations of an alien system typically do three things. First, they clarify the functioning ontology of the system and evaluate its status. Second, they try to make the system intelligible. Finally, they try to explain puzzling features of the system. Quantum mechanics presents many strange counter-intuitive features. Attempts to explain them away have failed. John Wheeler explained how one must learn to live with these puzzling features by adapting Gertrude Stein’s evaluation of modern art. “It looks strange, and it looks strange, and it looks very strange; and then suddenly it doesn’t look strange at all and you can’t understand what made it look strange in the first place” ( Wheeler, 1983: p. 185 ).
In this evaluation, we will focus first on the ontological issues and then on the general problem of making QM intelligible. On the grounds that QM is a principle, rather than a constructive theory, the evaluation of ontological issues will be based primarily on QFT and the standard model. The evaluation of QM is more general if one assumes that the basic features of QM will carry over to future quantum theories.
One lesson learned from the non-physics interpretations considered earlier is that the status of the functional ontology of a system is best evaluated from the perspective of a superior system. This carries over to physics. Newton attempted to ground mechanics on an ontology of hard, massy, impenetrable corpuscles. His successors effectively recast mechanics itself a foundation for the rest of science. This supported classical reality, a view of the world as a mechanistic deterministic system. When quantum mechanics assumed the role of the fundamental physical science then mechanistic determinism could be understood as the relative ontology of classical reality. It is reasonable to rely on this relative ontology in contexts where classical mechanics is the appropriate tool.
QFT is now the most basic science of physical reality. The status of its functional ontology would be best appraised in QFT could be evaluated from the perspective of a superior theory. Such a theory has not yet been developed. However, anticipations of the features such a theory should have supplied a tentative basis for such an evaluation. Our brief survey suggests two potential higher perspectives.
The first is an extrapolation from AQFT. From a programmatic perspective it might seem that interpretations based on algebraic formulations fit the pattern found in our non-physical examples. The natives, i. e., practicing physicists, rely on a simple particle ontology to ground a theory, the standard model, that does not admit of a rigorous mathematical formulation. AQFT supplies a more rigorous formulation. This assigns a foundational role to observables and seeks to explain away the physicists’ reliance on particles.
AQFT’s assumption of a superior status is undercut by the programmatic status of AQFT. Attempts to extend AQFt to the interactions treated in the standard model have not only failed. Thanks to the no-go theorems AQFT relies on, the program cannot even get off the ground. The Clay mathematics Institute offered it 2010 Millenium award of one million dollars to anyone who could put the standard model on a rigorous foundation. 2010 was the only year that a millennium prize was not awarded.
Ruetsche’s methodology suggests a possibility of relating AQFT to the standard model though a relaxation of rigor. In place of the pristine interpretation of pure theories, she advocates interpreting theories in problem solving contexts. AQFT’s inability to handle interactions stems from its insistence that observables supply the only data the theory uses. Her rejection of Algebraic Imperialism suggests the need for going beyond this limitation. The Hilbert Space Conservative privileges one Hilbert space for the formulation of QFT. A rejection of this conservatism might possibly lead to accepting separate Hilbert (or Fock) spaces for the separate components of the standard model. These however remain unrealized possibilities.
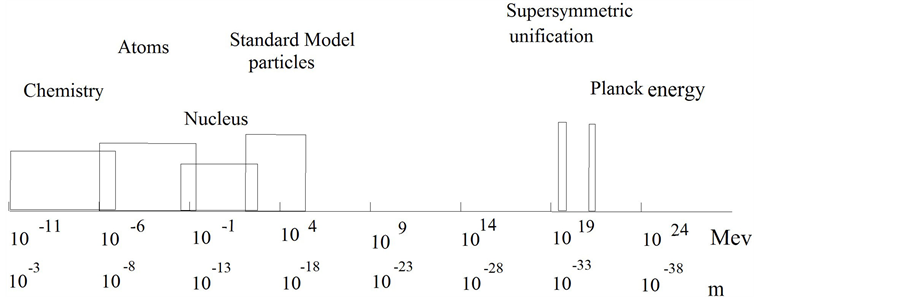
The interpretation of LQFT developed by Weinberg also suggests the possibility of evaluating QFT from the perspective of a successor theory. Present QFT is interpreted as an effective theory with a functional validity within a limited energy range. Figure 1 illustrates this for theories from chemistry to anticipated theories proper to the Planck level. The anticipated successor theories, which may not be a field theory should explain some of the parameters, such a particle masses and coupling constants, that are fed into the standard model by hand, based on experiments rather than theories. A successor theory might also be valid in the large energy gap separating the standard model from the Planck limit, where string theory, loop quantum gravity, or some yet to be developed theory might be valid. Interpreting LQFT as an effective field theory with an anticipated successor supplies a basis for appraising its functional ontology. It relies on a particle ontology without a commitment to particles playing a foundational role in successor theories. This ontological commitment is indispensable. It supplies a working foundation for treating strong, electromagnetic, and weak interactions in much the same way that a commitment to atoms supplies a foundation for treating chemical interactions. Local gauge theory entails sharply localized particle interactions. The localization is not specified within the observer’s framework. This undercuts the applicability of the AQFT arguments against sharp particle localization.
The interpretation of LQFT as an effective theory supplies a basis for appraising the path integral method. Calculations of the Lamb shift in the hydrogen atom have been carried out to ever higher orders involving multiple interactions with virtual particles generated by interactions with the vacuum14. The results exhibit the closest correspondence between theory and experiment in the history of physics. Critics avoid a literal interpretation of the Feynman diagrams and the virtual particles they involve. No one denies the contribution they make. A functional particle ontology involves a commitment to virtual as well as real particles.
These considerations lead to the deepest ontological problem in QFT, the vacuum, to use the entrenched misnomer. It enters QFT as a presupposition. A creation operator acting on the vacuum state produces a particle,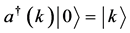
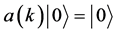
Figure 1. Interaction energies.
ticle. To use Ruetsche’s sounder principle, it is reasonable to anticipate that the vacuum will be a foundational presupposition of any future QFT. Some cosmologists attribute the origin of the universe to a vacuum fluctuation and assume that other fluctuations lead to other universes (see Tegmark 2014 ). If the vacuum is regarded as the ultimate source of all there is, then its status is the most fundamental problem in ontology. How should it be treated? Wilczek ( 2008 , Appendix B) argues that the vacuum should be regarded as a multilayered, multicolored, cosmic superconductor. However, he admits that he knows of no plausible hypothesis of its composition. It is unreasonable to expect philosophers to supply such an hypothesis. However, it is more unreasonable to expect them to continue ignoring the most fundamental ontological problem quantum mechanics presents.
We have been taking QM as a set of principles present in NRQM, QED, QFT, and presumably in any further successor theory. The interpretations of QM that we have considered have not, as far as I can see, made any significant contribution to the normal practice of physics. It contrasts with the pre-quantum situation. Helmholtz’s way of practicing physics was influenced by his study of Kant. Maxwell’s ideas on how theories should be developed and interpreted were conditioned by his philosophical mentor, William Whewell. Einstein cited Mach’s philosophical reflections as an influence on his development of relativity. Poincaré’s contributions to mathematics and physics were continuous with his philosophical endeavors. The architects of quantum physics made passing references to Plato, Aristotle, Kant, and William James. None cite philosophers of science or their interpretations.
The protracted efforts to interpret quantum physics have deepened philosopher’s awareness of the issues. They have also contributed to philosophical understanding of meta-questions concerning the status of philosophy and the limitations of accepted methodologies. The interpretative question: “What must the world be like if quantum mechanics is true of it?” oversimplifies the problematic of interpretation.
Interpretations of QM involve three world models. The life world is the world in which we live, and move, and have our being. Variations on common sense systematizations of this world have functioned as presuppositions in Aristotelianism, Thomism, Marxism, Pragmatism, Analysis, and Phenomenology. Classical reality is a model of what reality would be like if classical mechanics were the basic physical science. Since this omits such features of the Life World as life, consciousness, sensation, knowledge, and freedom, it was often supplemented by dualism. The Quantum Domain is the depth reality characterized by such distinctive features as distributed probability, superposition, interference, and entanglement. Since it is characterized by properties, rather than the objects that possess these properties, their study could be called idiontology16. QM applies to systems, which may be objects, collections of objects, interactions, or whatever.
Scheibe’s contribution to the question of what kind of systems QM applies to is the realization that QM applies strictly only to isolated systems. Such isolated systems are not directly know. He treated epistemological and statistical extension of this ontic core. The emphasis on statistical extensions seemed necessary at a time when many physicists accepted a statistical interpretation of superposition. The epistemological extensions terminate in a knower using a measuring apparatus. This raises questions concerning the status of the apparatus and the role of the knower.
For Bohr measurement is a feature of the life world involving choices made by an experimenter. In the orthodox interpretation measurement is a problem, not a foundation. The assumption that QM must cover the measuring process leads to two problematic issues. The first is the apparent inconsistency involved in relying on a projection postulate, distinct from the linear evolution of the system that reduces a superposition of states to a mixture of states with different probability coefficients. This generates the further question of how only one of these possibilities becomes real.
Hughes attempted to remove this inconsistency by an epistemological interpretation of the projection postulate. Healey rejected this postulate and appealed to differing perspectives to dissolve the discontinuity. Van Fraassen invoked superselection rules and reductionism as a means of avoiding the projection postulate. None of the solutions offered have been accepted as the solution. The projection postulate remains part of the normal practice of physics.
The second problem these interpretations focused on was incompleteness. The Einstein-Podolsky-Rosen paper argued for the reality of unmeasured observables. Bohr countered this ontological argument with the epistemological contention that the EPR assignment of values to unmeasured observables was not contextually meaningful. The orthodox interpretation insisted on the eigenfunction-eigenvalue rule. Observables have values only when the eigenfunction assigns them values. Both hidden variable theories and modal interpretations of QM developed ways of assigning values, dynamic values, beyond the values the eigenfunction assigns. No interpretation succeeded in attaching empirical significance to such value assignments. Nevertheless defenders of a modal interpretation argue that this assignment of values was significant in fleshing out the quantum domain.
The question of what the act of knowing contributes to the reality assigned to the known is the most venerable problem in philosophy, one to which Plato, Kant, and Hegel made significant contributions. It resurfaced in the earlier stages of the evolution of QM interpretations chiefly because of clashes between these interpretations and currently influential philosophical positions. Logical Positivists insisted on the priority of sense data and interpreted away any talk of theoretical entities. Both Marxist philosophers and the anti-Marxist, Karl Popper, associated the Copenhagen interpretation with Logical Positivism and attacked it as a form of subjectivism. The interpreters we have been considering have largely bypassed such objections either by focusing on the interpretation of the mathematical formalism or on the activities and dialogs of physicists.
We conclude with some reflections on what interpretations of QM might contribute to contemporary philosophy. The present situation can be described as a collection of conflicting fiefdoms. This divisiveness is primarily due to the general pattern of academic specialization. It is exacerbated by the partial polarization of much contemporary philosophy into analysis, phenomenology, philosophy of science, and historical studies. There were sustained efforts within the analytic tradition, and some sporadic efforts within the phenomenological tradition, to go beyond the comforting limits of ordinary language or the life world. These efforts, however, either ignored interpretations of QM or treated quantum physics as an extension of classical reality.
Husserl attributed the crisis of European science to a false notion of objectivity. This is the objectivity thought to characterize classical reality, not the quantum domain. Heidegger was stimulated to relate his existentialism to quantum physics by hearing a lecture of Heisenberg on the new physics ( Chevalley, 1990 ). The primary obstacle blocking such extensions is the fact that phenomenologists develop philosophy from a first person perspective. The efforts of Michel Bitbol, Catherine Chevalley, Patrick Heelan (2002), and a few others to relate phenomenology to quantum physics has won little support17.
Logical Positivism’s thesis of the unity of science seemed to embrace advances in physics. Their methodology, however, precluded a treatment of the distinctive features of QM. Carnap ’s Aufbau ( 1960 ) systematized the method of analyzing science by replacing scientific statements with collections of observation statements. Quine (1960) revitalized the unity of science thesis. His great sphere of knowledge had sense impressions on the periphery, physics just outside the core, which features standard logic and set theory. This grossly oversimplified: the life world by excluding persons, intentionality, intensions, and secondary qualities; and interpretations of QM incompatible with a reliance on classical logic.
Wilfrid Sellars set lofty all-inclusive goals for philosophy: “The aim of philosophy, abstractedly formulated, is to understand how things in the broadest possible sense of the term hang together in the broadest possible sense of the term.” ( Sellars, 1963: p. 1 ). To get the life world and ultimate physical reality he fashioned the stereoscopic spectacles of The Manifest Image and The Scientific Image. Since an adequate scientific image seemed unavailable, he used the logic of Wittgenstein’s Tractatus as a place holder. This, like Quine’s core, supports an ontology compatible with classical logic.
Bas Van Fraassen developed his version of constructive empiricism through a dialectical relation with his former mentor, Wilfrid Sellars. The crucial break centered on Van Fraassen’s development of a semantic conception of theories as collections of models augmented by hypotheses about the way aspects of reality are represented by these models. Sellars retained the syntactic conception of scientific theories as sets of propositions given a deductive ordering by inference rules. Van Fraassen has repeatedly criticized Sellars’s two images ( Van Fraassen, 1999 ; 2002 ). The metaphorical use of “image” is deemed misleading as is the associated idea it promotes that the practice of physics and ordinary living embody global views of reality. The issues they aim to systematize should be put in a pragmatic perspective of people coping with different problems in different ways. If theories are appraised for their empirical adequacy, rather than for their truth, then the clashes between differing perspectives is dissolved, or at least diluted.
When Van Fraassen treats the life world he focuses on particular issues and rejects all attempts to find a secure foundation for knowledge or global theories of everything. In this empirical stance he is able to relate accounts of quantum physics and scientific explanations to literature, painting, religious beliefs, and even irrational behavior. Rationality is bridled irrationality ( Van Fraassen, 2002 ). Thanks to his proficiency in phenomenology and the history of philosophy the individual items receive tailored considerations, rather than inclusion under the cloak of abstract global accounts.
I find his empirical stance, his rejection of foundationalism, and his pluralistic methodology quite attractive. Yet, a lingering residual realism supports a slightly fuzzy objection. Both propositions in ordinary discourse and scientific claims are regularly and reasonably accepted as true. Even without invoking a correspondence theory the common contention is that some claims are true because that is the way the world is. Any attempt to specify how the world is independent of our knowledge of it leads, in John Milton’s terms, to the “great Scythian bog wherein armies whole have sunk.” Yet, the conviction that there is a common reality underlying the life world and fundamental physics has induced significant attempts to relate life problems to the interpretation of QM.
The protracted debates between reductionists and emergentists presupposed classical reality to be the basic scientific representation of the world. This seemed to outlaw any science-based defense of emergence. A common strategy was to argue that accepted physics is incomplete and must be supplemented by something that allowed for emergence: entelechy, a goal-driven factor (Driesch); becoming as an ontological category (Bergson); non-physical forces (Broad); a distinction between radial and tangential energy (Teilhard de Chardin); the role of tacit knowledge (Polanyi); the primacy of iconocic over mathematical models (Harré); or vitalism (dualists of different stripes). The reinterpretation of classical reality as a model with a limited scope and of the quantum domain as embodying holistic properties afforded emergentists a scientific basis for their arguments ( Castellani 2002 ).
Another problematic situation in which the interpretation of QM makes a distinct contribution is the traditional mind-body problem. Kim (1963, p. 237) presents a dilemma, which he considers the most serious difficulty in the philosophy of mind. Accept the causal closure of the physical order and discount the ontological reality of consciousness and qualia, or accept their reality and deny the causal closure of the physical order. This is supported by Kim’s exclusion principle. A sufficient cause of an event excludes any appeal to another cause. If a personal decision can, in principle, be explained by a reduction to the properties of ultimate entities, then one cannot explain it in terms of intentions or purposes. This reductionist account presupposes classical determinism. Interpretations of QM as the basic science involve indeterminism. Thus, radioactive decay is explained statistically. The question of why a particular uranium atom decayed at a certain time has no meaningful answer.
These two examples share a similar strategy. They begin with life world considerations on life, consciousness, sensation, and intentionality. Then they reject explanations offered in a life world framework and substitute analyses proceeding through levels from a life world framework down to the ultimate level. One may discount such a strategy either along the lines of Van Fraassen’s methodological pluralism or by considerations of a hierarchical order of effective theories. But to make either the original arguments or their systematic rejection intelligible it is necessary to have some sort of Ariadne’s string extending from an ordinary language framework to the quantum domain.
Bohr initiated such a program. He was an ordinary language analyst in the mould of the later Wittgenstein. He ignored philosophical theories and kept muddling through a collection of classical concepts, which he interpreted as an extension of plain language, until he could interrelate them in a conceptual network that was adequate for the unambiguous reporting of experimental results. Though his analyses had sharply limited scopes they were broader than Oxford analysis in one crucial respect. A conceptual framework, to use Bohr’s term, was always open to conceptual revision. A conceptual framework, in his opinion is not an a priori given, It is something we inherit that is transmitted through a shared language. When new experiences do not fit, then critical thinkers are drawn to examine the presuppositions of the old framework and initiate modifications18. Bohr assumes that the conceptual framework of classical physics is a simplified extension and modification of an ordinary language framework. His treatment of quantum physics centered on the way this classical framework could be extended and must be restricted in quantum contexts. This process of conceptual extension and modification requires a more detailed analysis. My 2011 initiates such a conceptual-historical analysis. Much more remains to be done.
Cite this paper
EdwardMacKinnon, (2016) Why Interpret Quantum Physics?. Open Journal of Philosophy,06,86-102. doi: 10.4236/ojpp.2016.61009
References
- 1. Aczel, A. D. (2001). Entanglement: The Greatest Mystery in Physics. New York: Four Walls Eight Windows.
- 2. Albert, D. Z. (1992). Quantum Mechanics and Experience. Cambridge: Harvard University Press.
- 3. Albert, D., & Loewer, B. (1988). Interpreting the Many-Worlds Interpretation. Synthese, 77, 195-213. http://dx.doi.org/10.1007/BF00869434
- 4. Altmanspacher, H., & Primas, H. (2002). Epistemic and Ontic Quantum Realities.
- 5. Auyang, S. (1995). How Is Quantum Field Theory Possible? New York: Oxford University Press.
- 6. Bell, J. S. (1964). On the Einstein Podolsky Rosen Paradox. Physics, 1, 195-200.
- 7. Bitbol, M. (1996). Mécanique Quantique. Paris: Flammarion.
- 8. Bitbol, M. (1998). Some Steps towards a Transcendental Deduction of Quantum Mechanics. Philosophia Naturalis, 35, 299- 328.
- 9. Bitbol, M. (2002). Science as If Situation Mattered. Phenomenology and Cognitive Science, 1, 181-224. http://dx.doi.org/10.1023/A:1020328422900
- 10. Bitbol, M. (2007). Ontology, Matter and Emergence. Phenomenology and the Cognitive Sciences, 6, 293-307. http://dx.doi.org/10.1007/s11097-006-9041-z
- 11. Bub, J. (1974). The Interpretation of Quantum Mechanics. Dordrecht: D. Reidel. http://dx.doi.org/10.1007/978-94-010-2229-3
- 12. Busch, P., Grabowski, M., & Lahti, P. (1995). Operational Quantum Physics. New York: Springer Verlag.
- 13. Carnap, R. (1960). Der logische Aufbau der Welt. Berlin: Weltkeis Verlag.
- 14. Castellani, E. (2002). Reductionism, Emergence, and Effective Field Theories. Studies in History and Philosophy of Modern Physics, 33, 251-267. http://dx.doi.org/10.1016/S1355-2198(02)00003-5
- 15. Chevalley, C. (1990). La Physique de Heidegger. Les Etudes Philosophiques, No. 3, 289-311.
- 16. Conacher, D. J. (1967). Euripidean Drama: Myth, Theme and Structure. Toronto: University of Toronto Press.
- 17. Critchley, S., Schroeder, W. R., & Bernstein, J. (1998). A Companion to Continental Philosophy. Malden, MA: Blackwell.
- 18. Crossan, J. D. (1991). The Historical Jesus: The Life of a Mediterranean Jewish Peasant. San Francisco, CA: Harper.
- 19. Daneri, A., Loinger, A., & Prosperi, M. (1962). Quantum Theory of Measurement and Ergodicity Conditions. Nuclear Physics, 33, 297-319. http://dx.doi.org/10.1016/0029-5582(62)90528-x
- 20. Darrigol, O. (1992). From C-Numbers to Q-Numbers: The Classical Analogy in the History of Quantum Theory. Berkeley, CA: University of California Press.
- 21. Diecks, D. (1986). On the Relevance of the Bell Inequalities to the Problem of Locality in Quantum Mechanics. Physics Letters A, 117, 433-435. http://dx.doi.org/10.1016/0375-9601(86)90397-X
- 22. Feynman, R. P., Leighton, R. B., & Sands, M. (1963). The Feynman Lectures on Physics. Reading, MA: Addison-Wesley.
- 23. Halvorson, H., & Clifton, R. (2002). No Place for Particles in Relativistic Quantum Mechanics. Philosophy of Science, 69, 1-28. http://dx.doi.org/10.1086/338939
- 24. Hartmann, S. (2001). Effective Field Theories, Reductionism and Scientific Explanation. Studies in History and Philosophy of Modern Physics, 32B, 267-304. http://dx.doi.org/10.1016/S1355-2198(01)00005-3
- 25. Healey, R. A. (1989). The Philosophy of Quantum Mechanics: An Interactive Interpretation. Cambridge: Cambridge University Press. http://dx.doi.org/10.1017/CBO9780511624902
- 26. Hertz, H. (1962). Electric Waves. New York: Dover Reprint (Original, 1892).
- 27. Honner, J. (1987). The Description of Nature: Niels Bohr and the Philosophy of Quantum Physics. Oxford: Clarendon Press.
- 28. Howard, D. (2004). Who Invented the “Copenhagen Interpretation”: A Study in Mythology (pp. 669-682). East Lansing, MI: Philosophy of Science Association.
- 29. Hughes, R. I. G. (1989). The Structure and Interpretation of Quantum Mechanics. Cambridge, MA: Harvard University Press.
- 30. Kane, G. (2000). Supersymmetry. Cambridge, MA: Perseus Publishing.
- 31. Kaplan, D. (2005). Five Lectures on Effective Field Theory. arXiv:nucl-th/0510023v1
- 32. Kim, J. (1963). Philosophy of Mind. Boulder, CO: Westview Press.
- 33. Kochen, S. (1985). A New Interpretation of Quantum Mechanics (pp. 1-2). Teaneck, NJ: World Scientific Publishing Co.
- 34. Lévi-Strauss, C. (1963). Totemism, Translated by Rodney Needham. Boston, MA: Beacon Press.
- 35. London, F., & Bauer, E. (1939). The Theory of Observation in Quantum Mechanics. In Wheeler and Zurek (pp. 217-259). Princeton, NJ: Princeton University Press.
- 36. Mackey, J. (1963). The Mathematical Foundations of Quantum Mechanics. New York: Benjamin.
- 37. MacKinnon, E. (1982). Scientific Explanation and Atomic Physics. Chicago, IL: University of Chicago Press.
- 38. MacKinnon, E. (2007). Schwinger and the Ontology of Quantum Field Theory. Foundations of Science, 12, 295-323. http://dx.doi.org/10.1007/s10699-007-9109-4
- 39. MacKinnon, E. (2008). The Standard Model as a Philosophical Challenge. Philosophy of Science, 75, 447-457.
- 40. MacKinnon, E. (2009). The Consistent Histories Interpretation of Quantum Mechanics. PhilSciArchives # 4549.
- 41. MacKinnon, E. (2011). Interpreting Physics: Language and the Classical/Quantum Divide. Amsterdam: Springer.
- 42. Malinowski, B. (1953 ). Argonauts of the Western Pacific. New York: E P. Dutton.
- 43. Manohar, A. (1996). Effective Field Theories. arXiv:hep/9606
- 44. Maxwell, J. C. (1954). A Treatise on Electricity and Magnetism. New York: Dover Reprint.
- 45. Mehra, J., & Rechenberg, H. (1982). The Quantum Theory of Planck, Einstein, Bohr, and Sommerfeld Its Foundation and the Rise of Its Difficulties, 1900-1925. New York: Springer-Verlag.
- 46. Petruccioli, S. (1993). Atoms, Metaphors and Paradoxes: Niels Bohr and the Construction of a New Physics. I. McGilvray, Trans. Cambridge: Cambridge University Press.
- 47. Quine, W. V. O. (1960). Word & Object. Cambridge, MA: The MIT Press.
- 48. Robinson, D. (1994). Can Superselection Rules Solve the Measurement Problem? British Journal for Philosophy of Science, 45, 79-93. http://dx.doi.org/10.1093/bjps/45.1.79
- 49. Ruetsche, L. (2002). Interpreting Quantum Field Theory. Philosophy of Science, 69, 348-378. http://dx.doi.org/10.1086/341047
- 50. Ruetsche, L. (2011). Interpreting Quantum Theories. Oxford: Oxford University Press.
- 51. Scheibe, E. (1973). The Logical Analysis of Quantum Mechanics. D. B. Sykes, Trans. Oxford: Pergamon Press.
- 52. Schwinger, J. (1983). Renormalization Theory of Quantum Electrodynamics. In L. Brown, & L. Hoddeson, (Eds.), The Birth of Particle Physics (pp. 329-353). Cambridge: Cambridge University Press.
- 53. Segal, C. (1986). Interpreting Greek Tragedy: Myth, Poetry, Text. Ithaca, NY: Cornell University Press.
- 54. Seibt, J. (2002). Quanta, Tropes, or Processes: Ontologies for QFT beyond the Myth of Substance. In M. Kuhlmann, H. Lyre, & A. Wayne (Eds.), Ontological Aspects of Quantum Field Theory (pp. 53-97). Hackensack, NJ: World Scientific. http://dx.doi.org/10.1142/9789812776440_0003
- 55. Sellars, W. (1963). Philosophy and the Scientific Image of Man. In W. Sellars (Ed.), Science Perception and Reality (pp. 1-40). London: Routledge and Kegan Paul.
- 56. Simon, P. (2002). Candidate General Ontologies for Situating Quantum Field Theory. In M. Kuhlmann, H. Lyre, & A. Wayne (Eds.), Ontological Aspects of Quantum Field Theory (pp. 33-52). Hackensack, NJ: World Scientific. http://dx.doi.org/10.1142/9789812776440_0002
- 57. Tegmark, M. (2014). Our Mathematical Universe: My Quest for the Ultimate Nature of Reality. New York: Knopf.
- 58. Teller, P. (1995). An Interpretive Introduction to Quantum Field Theory. Princeton, NJ: Princeton University Press.
- 59. Van Fraassen, B. (1991). Quantum Mechanics: An Empiricist View. Oxford: Clarendon Press. http://dx.doi.org/10.1093/0198239807.001.0001
- 60. Van Fraassen, B. (1999). The Manifest Image and the Scientific Image. In D. Aerts (Ed.), Einstein Meets Magritte: The White Book—An Interdisciplinary Reflection (pp. 29-52). Dordrecht: Kluwer. http://dx.doi.org/10.1007/978-94-011-4704-0_3
- 61. Van Fraassen, B. (2002). The Empirical Stance. New Haven, CT: Yale University Press.
- 62. Weinberg, S. (1995). The Quantum Theory of Fields. Cambridge, New York: Cambridge University Press. http://dx.doi.org/10.1017/CBO9781139644167
- 63. Wheeler, J. (1983). Law without Law. In J. Wheeler, & W. Zurek (Eds.), Quantum Theory and Measurement (pp. 182-216). Princeton, NJ: Princeton University Press. http://dx.doi.org/10.1515/9781400854554
- 64. Wigner, E. P. (1967). Symmetries and Reflections: Scientific Essays. Bloomington, IN: Indiana University Press.
- 65. Wilczek, F. (2008). The Lightness of Being: Mass, Ether, and the Unification of Forces. New York: Basic Books.
NOTES
1This brief summary relies on the detailed analyses of Conacher 1967 and Segal 1986 .
2Principia, Book 1, Prop. 69, “Scholium”.
3Principia, Book 3, Rule 3 of Reasoning in Philosophy.
4A more detailed account of this transition can be found in MacKinnon 1982 , chapt. 1.
5Steven Weinberg discussed the role of effective field theories in the Preface to Weinberg 1995 . More technical accounts may be found in Kaplan 2005 and Manohar 1996 . Kane (2000, chap 3) extended the notion from field theories to physical theories in general. Here we are following Kane’s precedent. Philosophical evaluations of effective theories are given in Hartmann 2001 and Castellani 2002 .
6One may consult Omnès 1999 or MacKinnon 2009 for an interpretation of the Consistent Histories formulation Albert and Lower 1998 and Wallace 2012 for the Everett, or many worlds, interpretation.
7A very detailed treatment of these problems may be found in Mehra & Rechenberg 1982 , Vol. 1, Part 2.
8More detailed treatments of the development of Bohr’s account of complementarity may be found in Honner 1987 , Darrigol 1992 , Part B, and in Petruccioli 1993 .
9See Howard 2004 for the origin of the Copenhagen interpretation.
10In a conversation with Abner Shimony Wigner claimed: “I have learned much about quantum theory from Johnnny, but the material in Chapter Six Johnny learned all from me” (citation from Aczel, 2001: p. 102 ).
11 MacKinnon 2008 argues that LQFT and the standard model should be the target for philosophical interpretations, rather than algebraic formulations. Fraser 2007 argues for the priority of AQFT.
12 Ruetsche 2011 , chap. 4 presents a concise account of the algebras involved in AQFT.
13 MacKinnon 2007 gives an evaluative survey of his development.
14A cornucopia of such diagrams and the calculations they support is given in Schweber 1962, chap. 15.
15“Therefore the ultimate substratum is of itself neither a particular thing nor of a particular quantity nor otherwise positively characterized; nor yet is it the negation of these, for negations will also belong to it only by accident”, Aristotle, Metaphysics, Book VII, 1029a23.
16Christian Wolff coined “ontology” from the classical Greek terms, òn, being, and logos, study. I enlarged this by adapting the term, idìon, that Aristotle used for characteristic properties.
17None of the 56 articles in The Companion to Continental Philosophy ( Critchley et al., 1998 ) treats the relation of Continental philosophy to the physical or biological sciences.
18This interpretation of Bohr was developed in detail in an unpublished lecture by Catherine Chevalley, “Philosophy and the Copenhagen Interpretation of quantum theory”. I am indebted to her for a copy of the paper and for enlightening discussions of the issues involved.