Open Journal of Forestry
Vol.05 No.04(2015), Article ID:55464,12 pages
10.4236/ojf.2015.54035
Quantifying Growth Responses of Black Spruce and Jack Pine to Thinning within the Context of Density Management Decision-Support Systems
Peter F. Newton
Canadian Wood Fibre Centre, Canadian Forest Service, Natural Resources Canada, Sault Ste. Marie, Canada
Email: peter.newton@NRCan-RNCan.gc.ca
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 January 2015; accepted 7 April 2015; published 9 April 2015
ABSTRACT
Models for quantifying the growth responses of black spruce (Picea mariana (Mill) BSP.) and jack pine (Pinus banksiana Lamb.) to precommercial thinning (PCT) treatments were developed. They accounted for the increased rate of stand development arising from PCT treatments through temporal adjustments to the species and site specific mean dominant height-age functions. Analytically, they utilized a relative height growth modifier consistent with observed density-dependent height repression effects. A phenotypic juvenile age-mature age correlation function was used to account for the intrinsic temporal decline in the magnitude of the PCT effect throughout the rotation. The resultant stand development patterns were in accord with theoretical and empirical expectations when the response models were integrated into algorithmic variants of structural stand density management models.
Keywords:
Structural Stand Density Management Models, Height Repression, Phenotypic Juvenile Age-Mature age Correlation, Precommercial Thinning

1. Introduction
Operationally, density management decision-support models are intended to assist forest managers in their determination of the optimal crop plan or stand developmental pathway that is required to realize a specified stand-level management objective. These objectives include: 1) maximizing net production by maintaining optimal site occupancy levels throughout the rotation (e.g., Newton, 2006a ); 2) accelerating stand operability status by reducing the length of the rotation required to attain a specified piece-size and/or merchantable volume threshold through the application of precommercial thinning (PCT) treatments (e.g., Newton, 1997 ); 3) enhancing end-product quality and increasing economic worth via commercial thinning treatments (e.g., McKinnon et al., 2006 ); 4) improving wildlife habitat potentials and increasing biodiversity by manipulating stand structures and managing course woody debris levels using stand interventions involving thinning treatments (e.g., Sturtevant et al., 1996 ); or 5) reducing wildfire risk by maintaining non-continuous vertical crown profiles through density control (e.g., Gómez-Vázquez et al., 2014 ).
A family of density management decision-support tools that are based on the modelling approach used to construct stand density management diagrams (SDMDs) have found global utility in the management of numerous temperate, boreal and tropical stand-types. These models have evolved in an incremental and sequential fashion over the last 50 years. Based on ecological concepts and quantitative relationships derived from initial spacing and thinning experiments, the first generation “static SDMDs” were developed by Ando (1962) in Japan for managing Japanese red pine (Pinus densiflora Sieb. et. Zucc.) plantations. They were later introduced into the Pacific Northwest region of North America by Drew and Flewelling (1979) and used to derive density control schedules for coastal Douglas Fir (Pseudotsuga menziesii (Mirb.) Franco) plantations. In order to explicitly account for density-dependent mortality losses arising from self-thinning via the use of size-density trajectory sub- models, second generation “dynamic SDMDs” were developed and calibrated for black spruce (Picea mariana (Mill) BSP) stand-types in central and eastern Canada by Newton and Weetman (1993, 1994) and later for other species including balsam fir (Abies balsam (L.)) stand-types in eastern Canada (Penner et al., 2006) . The third generation “structural stand density management models” (SSDMMs) were first introduced for black spruce stand-types in eastern and central Canada. SSDMMs included the ability to forecast stand structural attributes employing predictions derived from the SDMD-based models (Newton et al., 2004, 2005) . Specifically, the SDMD model structure was expanded through the integration of Weibull-based parameter prediction equation systems for recovering diameter distributions. Through further model expansion in terms of including additional recovery modules for predicting end-products and economic values, above-ground biomass and carbon yields by diameter class, the fourth generation “modular-based SSDMM” was developed and subsequently calibrated for jack pine (Pinus banksiana Lamb.) stand-types in central Canada (Newton, 2009) .
Model development is an ongoing and iterative process and consequently the SDMD-based modelling platform would be expected to evolve as modelling innovations are introduced and forest management objectives change. These new variants will increase the utility of SDMD-based models in forest management decision-making. However, one key outstanding analytical shortcoming common to all the SDMD-based models irrespective of their generation, is the lack of response functions for quantifying growth responses to PCT treatments. Specifically, the current model specifications do not explicitly account for the accelerated rate of tree growth which occurs once the residual crop trees have rebuilt their photosynthetic apparatus (crowns) and acquired additional site resources (nutrients and moisture) following thinning. Although this modeling deficiency has not negated the deployment of SDMD-based models in operational forest management planning ( McKinnon et al., 2006) , post-thinning yield forecasts may nevertheless be underestimated (sensu García, 2012 ). Consequently, the purpose of this study was to address this shortcoming by developing thinning response sub-models for natural-ori- gin black spruce and jack pine stand-types, subsequently integrate them into the modular-based SSDMM architecture, and demonstrate their resultant utility in density management decision-making. Although the parameterization of the models is species-specific, the modeling approach is also applicable to past generations of the SDMD-based models.
Conceptually, the analytical approach utilized in developing the thinning response models falls within the treatment modifier equation class of methodologies use to model growth responses to silvicultural treatments ( Weiskittel et al., 2011 ). This involves modifying the functions which quantify or drive temporal change within growth and yield simulators through the addition of rate parameter modifiers. The modifiers attempt to account for the changed temporal dynamics arising from the specific silvicultural treatment. The treatment modifier equation approach has been used previously for modeling responses to tree improvement (Newton, 2003, 2015a; Xie and Yanchuk, 2003) and forest fertilization (Newton and Amponsah, 2007) , in addition to other silvicultural treatments (see Weiskittel et al. (2011) for a comprehensive summary).Furthermore, as introduced in this study, the use of a correlative-based dissipation factor to account for the anticipated temporal decline in thinning responses over time, extends the utility of the modifier equation approach.
2. Methods
2.1. Development of Height Growth Modifier Functions
The modeling approach used to quantify the effect of density reductions arising from PCT treatments was through an empirical-based adjustment to the site-based mean dominant height-age function. The adjustment was modelled to mimic the temporal inverted u-shaped response pattern that was previously observed for these species (Newton, 2004) . Specifically, the growth response was assumed to follow a nonlinear symmetrical pattern: initially increasing, reaching an asymptote value, thereafter rapidly declining due to crown re-closure and eventually vanishing upon the reoccurrence of density-dependent mortality (self-thinning). Consequently, the response was modelled to initiate immediately following the completion of the response delay period, then increase in a linear fashion until a threshold maximum is achieved and thereafter dissipated according to a phenotypic juvenile age―mature age trait-based (mean dominant height) correlation model.
The density-dependent height repression coefficient for jack pine (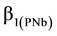 (m/stems/ha) Equation (1a) and black spruce (
(m/stems/ha) Equation (1a) and black spruce (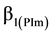 m/stems/ha); Equation (1b) were used to formulate 2 response model variants.
m/stems/ha); Equation (1b) were used to formulate 2 response model variants.
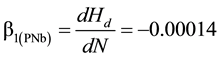 (1a)
(1a)
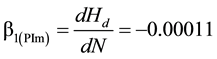 (1b)
(1b)
where Hd and N are mean dominant height (m) and stand density (stems/ha), respectively. These coefficients were derived from 24 forty year-old Nelder plots which exhibited stand developmental characteristics consistent with an asymptotic yield-density condition and hence were considered as maximum values and applicable at a stand age of 40 yr. Refer to Newton (2015b) for complete analytical details underlying the determination of the repression coefficients.
In order to provide an estimate of the rate of change in Hd expected for given unit change in N arising from PCT, the height growth repression coefficients were used (Equations (1a) and (1b)). For example, a density reduction from 10,000 to 2000 stems/ha would yield an increase of 1.12 m in Hd for jack pine and 0.96 m in Hd for
black spruce. Equation (2) re-expresses this increase into a percentage value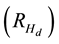 .
.
 (2)
(2)
where Hd(40) is the dominant height (m) at an age of 40 yr derived from the site-specific mean dominant height- age functions, and NPRE and NPOST are the stand densities before and after the PCT treatment, respectively. For example, according to Equations (1a) and (2) in combination with the mean dominant height-age function developed by
Carmean et al. (2001)
for jack pine, a stand situated on a good quality site (site index = 17) with a PCT treatment implemented at age 10 in which 7100 stems/ha were removed, would yield a Hd(40) estimate of 15.3 m. This would represent an increase of 1.0 m over its nominal height value at age 40. Hence the calculated 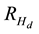 at age 40 years would be 7%. Given that the 1) density-dependent height repression effect increases over time as the degree of site occupancy increases, and 2) virtually all of the initial spacing treatments on the Nelder plots which were used to establish the repression coefficients had experienced suppression-related mortality by age 40, it was assumed that a state of asymptotic (full) occupancy had been achieved and further increases in height repression effects would be unlikely or inconsequential. Consequently, the percentage increase calculated via Equation (2) is assumed to be the empirical maximum for these species and is denoted as the “maximum response model variant”.
at age 40 years would be 7%. Given that the 1) density-dependent height repression effect increases over time as the degree of site occupancy increases, and 2) virtually all of the initial spacing treatments on the Nelder plots which were used to establish the repression coefficients had experienced suppression-related mortality by age 40, it was assumed that a state of asymptotic (full) occupancy had been achieved and further increases in height repression effects would be unlikely or inconsequential. Consequently, the percentage increase calculated via Equation (2) is assumed to be the empirical maximum for these species and is denoted as the “maximum response model variant”.
The second response model variant is identical to the first one but with the exception that the repression coefficients were proportionally reduced. Specifically, it was set to be equivalent to 25% of the maximum repression value in order to account for the occurrence of a potential minimal temporal change in the height-density relationship. This threshold was determined from the observed repression coefficients observed on the Nelder plots at the earlier stages of stand development (e.g., jack pine between ages 16 and 20 had a mean repression coefficient of 0.000037 versus its value at 40 years of 0.000137 (Newton, 2015b) ). Based on the minimum response model, a PCT treatment in which density is reduced from 10,000 to 2000 stems/ha would yield a 0.3 m or 2% height increase at age 40 for jack pine.
2.2. Projecting the Thinning Response over the Rotation
The height repression effect increased with site occupancy and eventually reached an asymptotic level (Newton, 2015b) . To reflect this increasing trend, the percentage increase was distributed in a proportional fashion to the height-age function. Specifically, it initiated at the time of the completion of the response delay period immediately following thinning and continued to and maximized at an age of 40 yr (Equation (3)).
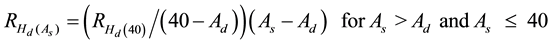 (3)
(3)
where 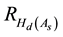 is the percentage increase in Hd at age As due to the PCT treatment,
is the percentage increase in Hd at age As due to the PCT treatment, 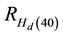 is the percentage in-
is the percentage in-
crease in Hd at age 40 as calculated from Equation (2), and Ad is the stand age at the completion of the response delay period immediately following the PCT treatment. As stated above, it was assumed that the repression effect was fully expressed by age 40. This was based on the height development patterns observed across a wide range of density conditions on the Nelder plots which were used to determine the presence of density-depen- dent height repression for these species (Newton, 2015b) .
Thereafter the percentage increase was modelled to decline according to a phenotypic juvenile age―mature age correlation model. The model was calibrated using the jack pine remeasurement data obtained from 28 Nelder plots at ages 16, 20 and 40 yr (post-establishment). Briefly, these plots belonged to 1 of 3 geographically-separated clusters that were located within the Missinaibi-Cabonga forest section of the Canadian Boreal Forest Region (B.7; Rowe 1972 ). Cluster 1 consisted of 10 Nelder plots established on well drained sites with medium to fine sandy soil textures within the township of Dunmore, Ontario. Cluster 2 included 10 Nelder plots established on well drained medium sandy loam soils within township of Willison, Ontario. Cluster 3 was composed of 8 Nelder plots which were established on well drained medium sandy soils within Terry Township, Ontario. The clusters consisted of a rectangular-like grouping of individual plots in which no individual plot was greater than 500 metres from its closest adjacent plot. Structurally, each Nelder plot was 0.785 ha in size and designed according to the 1a configuration described by Nelder (1962) : 60 equally-spaced (360/60 = 6˚ between spokes) 47 m spokes which were randomly subdivided into twelve 5-spoke monospecific sectors comprised of jack pine, black spruce or white spruce (Picea glauca Moench). Radiating from the plot centre and starting approximately 4.74 m along each spoke, 24 trees were planted at geometrically increasing intertree distances. This resulted in a circular design consisting of 24 concentric circles with 12 species-specific 5-spoke sectors radiating out from the plot centre. Intertree distances ranged from 0.5 m to 4.32 m and associated nominal densities ranged from 429 to 42,698 trees/ha. In total, 1440 trees were planted within each plot: 24 trees/spoke × 5 spokes/sector × 4 sectors/species × 3 species/plot. All the Nelder plots were established on sites that were mechanically prepared using 2 + 0 bare-root nursery stock and subjected to subsequent replacement planting and/or vegetation management treatments (brushing and/or herbicides), if required. Planting operations took place over a 2 year period (1968-1969) and plot remeasurements consisting of breast-height diameter―outside bark (cm), crown width (m), height to live crown base (m) and total height (m) measurements, were obtained on jack pine in 1984, 1988 and 2008.
Analytically, the approach employed is based on the model developed by Lambeth (1980) for projecting genetic worth effects. Specifically, a juvenile age-mature age correlation model was utilized. The model was parameterized using a 2-step procedure: 1) obtaining the significant (p ≤ 0.05) correlation coefficients (r) between Hd’s for the age pairs of 16 - 40, 20 - 40 and 16 - 20; and 2) regressing the significant r’s against the natural logarithm of the age pair ratios (A1/A2 where A1/A2 = 16/40, 20/40, or 16/20). The first step yielded 57 significant coefficients from the 84 possible relationships (3 relationships per plot × 28 plots). The second step resulted in the correlation model given in Equation (4).
 (4)
(4)
The resultant regression statistics and associated residual analysis indicated satisfactory fit statistics and residual patterns: r2 = 0.368; SEE = 0.11; F-ratio = 32* (p ≤ 0.05)); and normality of raw residual distributions with no evidence of non-constant variance. The age-dependent percentage increase in Hd due to thinning (density reduction) was modeled using Equation (5) and is similar to the approach used to project genetic worth effects (i.e., GHr equation in Xie and Yanchuk (2003) ).
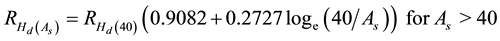 (5)
(5)
where  is the percentage increase in Hd at age As due to a PCT treatment, and
is the percentage increase in Hd at age As due to a PCT treatment, and 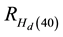 is the percentage
is the percentage
increase in Hd at age 40 as calculated from Equation (2). Essentially, the correlation and hence the gain declines as the difference between the time of the occurrence of the maximum effect (40 yr) and the requested age increases. Note, Equation (4) and Equation (5) were used for both species given the lack of calibration data available to establish the correlation model for black spruce.
2.3. Integration of the Response Models into SSDMMs and Demonstration of Their Utility
SSDMMs have been developed for natural-origin stand-types consisting of monospecific jack pine and black spruce even-aged stands situated on upland mineral soils (Newton, 2009, and 2012c) . The algorithmic analogues of these SSDMMs provide site-specific estimates of volumetric yields, diameter distributions, tree heights, log assortments, components-specific biomass and carbon outcomes, sawmill-specific products and associated fiscal values, and fibre quality attributes for a specified crop plan. The crop plan includes information pertaining to initial densities, thinning treatments, merchantable specifications, operational adjustment factors, degrade factors, cost profiles, and rotation lengths. The principal relationships which govern stand development within the SSDMMs are embedded in the dynamic SDMD module (e.g., see Figure 1 in Newton (2009, 2012c) ). Hence the thinning response models were incorporated within this module in accord with the following computational script.
Figure 1. Site-specific dominant height-age curves for unthinned (unfilled circles) and thinned (filled circles) stands with the embedded minimum (bottom) and maximum (top) increases arising from the PCT-based density reductions. The natural-origin jack pine (left-hand side) and black spruce (right-hand side) stands with an initial establishment densities of 10,000 stems/ha situated on medium site qualities (site index of 17 m) were PCT at 10 years of age in which 7100 stems/ha were removed.
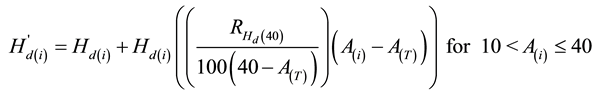 (6)
(6)

where
or
and 

In order to demonstrate the utility of the models within density management decision-making, the modified algorithmic analogues of the SSDMMs were used to simulate operationally relevant crop plans. These involved the application of PCT treatments within density-stressed natural-origin black spruce and jack pine stand-types. The simulations included both of the response model variants (maximum and minimum formulations). More specifically, for each species, the simulation involved a scenario in which 3 identical stands which had naturally established at initial densities of 10,000 stems/ha following a stand-replacing disturbance event (clear-cut harvesting) on good quality sites (17 m site index), were subjected to 1 of following 3 treatments: 1) no thinning (Regime 1; control); 2) a single PCT treatment at age 10 employing the maximum thinning response model to project post-treatment stand development (Regime 2); and 3) similar to Regime 2, a single PCT treatment at age 10 yr but using the minimum thinning response model to project post-treatment stand development (Regime 3). In order to account for density-independent mortality throughout the rotation, an operational adjustment factor (OA) of 0.01%/yr was specified for all 3 regimes. The fixed costs included a $0.1 K/ha regeneration assessment fee applicable at the time of establishment and $0.3 K/ha charge for the PCT treatment (e.g., labour and supplies for equipment). Variable costs associated with stumpage and renewal fees, harvesting, transportation and manufacturing differed by regime in order to reflect the nominal cost reductions arising from larger piece sizes and spatial uniformity within the treated stands (i.e., $90/m3 for the control stand versus $80/m3 for the treated stands). The time of simulation was set to year 2014, inflation and discount rates were set to 2% and 4%, respectively, and a 10% degrade factor was used for all 3 regimes. Operability targets were defined by a threshold piece size of 12 stems/m3 and merchantable volume yield of 150 m3/ha.
3. Results and Discussion
3.1. Temporal Response Patterns
Literature-based experimental results summarized via meta-analyses combined with analysis of growth patterns within destructively sampled trees sampled from comparable unthinned and thinned research plots, suggests that boreal conifers are responsive to PCT treatments in terms of the magnitude and duration of their growth and yield responses (Newton, 2004, 2015b) . Specifically, based on review of 22 black spruce PCT experiments and 46 jack pine PCT experiments reported in the literature, Newton (2004) found that after accounting for treatment-induced diameter truncation effects, both species exhibited positive diameter yield responses, relative to unthinned control plots. However, the pattern of the responses were characterized by a nonlinear inverted u-shaped pattern which varied in magnitude and duration depending on thinning intensity, time of treatment and site quality. Newton (2015b) reported similar results based on growth patterns within individual trees derived through destructive stem analysis: thinned trees exhibited a relative growth response pattern which was characterized by an initial period of rapid increase followed by the attainment of a plateau which thereafter declined and eventually vanished over time. Quantitatively, Equations (6) and (7) as presented within the computational script are consistent with this observed temporal response pattern. Figure 1 exemplifies the effect of the maximum and minimum response models on the height-age trajectories relative the unthinned control stands. In these examples, natural-origin jack pine and black spruce stands with an initial establishment density of 10,000 stems/ ha situated on a site index of 17 m were PCT at 10 yr during which 7100 stems/ha were removed and grown until a rotation age of 80 yr. Note, the site-specific height-age functions developed for jack pine and black spruce by Carmean et al. (2001) and Carmean et al. (2006) , respectively, were used.
Ecologically, responses to PCT are partially dependent on the nature of resource competition processes occurring within the stands preceding treatment. In an asymmetric competition relationship in which larger-sized individuals are able to obtain a greater relative share of the finite resources than are the smaller-sized trees (e.g., a competition process involving light; Newton and Jolliffe, 1998 ), removing smaller-sized trees may have a minimal effect on the residual crop. Conversely, a symmetric competition relationship in which all sized trees are able to obtain a size-proportional equal share of the finite resources (e.g., a competition process involving nutrients and/or moisture; Newton and Jolliffe, 1998 ), removing smaller-sized trees via PCT may enhance the growth rate of the residual crop given the increased availability of these growth-limiting resources. The relative response patterns observed in this study are reflective of the differential between thinned and unthinned stands in terms of their responses to increasing and decreasing resource levels. The reduction in density-stress via the PCT treatment reallocates critically required resources to the residual crop trees resulting in positive growth gains. Furthermore, the rapid maximization of the response to PCT may be partially reflective of a synergistic effect arising from a short-term fertilization effect (decomposition of the thinned trees on the forest floor) in combination with an overall increase in moisture and light resources. However, as the thinned stands start to re-close and regain full site occupancy, the thinning effect rapidly diminishes. Individual tree growth rates decline resulting in the eventual collapse of positive growth responses with associated increases in density-dependent mortality (self-thinning) due to increasing density-stress. Baldwin et al. (2000) in a comprehensive analysis of a long-term spacing and thinning experiment involving loblolly pine (Pinus taeda L.) reported similar results in terms of relative density: the level of intraspecific competition as measured by Reineke’s stand density index within the control and thinned plots were approaching equivalence, approximately 38 yr after treatment. Collectively, these external results are in accord with the generality of the model specifications presented in this study.
3.2. Demonstrated Utility and Evaluation of the New Response Models
Employing the traditional stand density management diagram graphic, the resultant temporal mean volume- density trajectories for each of the 3 regimes are illustrated within Figure 2 by species. Note, the stands at the time of the PCT treatment (10 yr) were below the x-axis and hence hidden. However based on tabular output, the jack pine and black spruce stands at the time of thinning had mean dominant heights of 4.3 and 2.9 m, respectively, densities of 9955 stems/ha, mean volumes of 0.1 dm3, quadratic mean diameters of 1.0 and 0.9 cm, respectively, basal areas of 0.7 and 0.9 m2/ha, respectively, and relative density indices of 0.02 and 0.06, respectively. Rotational yield estimates are provided in Table 1 and stand-level performance metrics are given in Table 2.
The stands subjected to PCT attained higher levels of site occupancy irrespective of species or response model as evident by their greater mean size-density conditions at rotation (Figure 2). Contrasting the yield estimates for the unthinned stand with the PCT stands employing the maximum and minimum response models for each species revealed the following (n., percentages correspond to the maximum and minimum response models by jack pine followed by corresponding values for black spruce): PCT stands (1) had greater rotational mean tree sizes (heights (5% and 2%; 4% and 1%), diameter (30% and 21%; 18% and 12%) and volumes (82% and 25%; 52% and 34%)), (2) attained lower levels of stocking and site occupancy (basal area (−24% and −30%; −9% and −13%) and relative density index (−28% and −33%; −15% and −18%)), (3) produced smaller total volumes (−20% and −29%; −2% and −9%) and merchantable volumes (−19% and −28%; −1% and −9%), (4) produced a fewer number of pulplogs (−48% and −46%; −55% and −42%) but a greater number of sawlogs (78% and 48%; 45% and 26%), (5) had reduced volumes of recoverable products irrespective of mill-type with the exception of the stud-mill lumber volumes for black spruce (chip (−37% and −38%; −14% and −17%) and lumber (−12% and −18%; 6% and −5%), and (6) higher economic worth irrespective of mill-type processing configuration (34% and 30%; 27% and 10%).


Figure 2. (a) SDMD graphic for the natural-origin jack pine stand-type: expected 80 year size-density trajectories with 1 year intervals denoted by a vertical line for each of the 3 user-specified crop plans, for stands situated on good quality sites (SI = 17). Specifically: Regime 1―establishment density of 10,000 stems/ha with no thinning; Regime 2―establishment density of 10,000 stems/ha with a PCT of 7100 stems/ha at age 10 yr employing the maximum thinning response model; and Regime 3―establishment density of 10,000 stems/ha with a PCT of 7100 stems/ha at age 10 yr employing the minimum thinning response model. Principal components of the SDMD: i) isolines for mean dominant height (Hd; diagonal lines ranging from a minimum of 8 m at the bottom of the graphic to a maximum of 24 m at the top of the graphic separated by 2 m increments), quadratic mean diameter (Dq; horizontal-line lines ranging from a minimum of 4 cm at the bottom of the graphic to a maximum of 26 cm at the top of the graphic separated by 2 cm increments), mean live crown ratio (Lr; 35% (highest dashed diagonal line), 40%, 50%,…, 80% (lowest dashed diagonal line)),and relative density index (Pr; 0.1 - 1.0 by 0.1 intervals (diagonal lines)); ii) crown closure line (lower diagonal solid line) and self-thinning rule at a Pr = 1.0 (upper diagonal solid line); and iii) lower and upper relative density (Pr) diagonal isolines delineating the optimal density management window (Dm; 0.32 ≤ Pr ≤ 0.45); (b) SDMD graphic for the natural-origin black spruce stand-type: expected 80 year size-density trajectories with 1 year intervals denoted by a vertical line for each of the 3 user-specified crop plans, for stands situated on good quality sites (SI = 17). Specifically: Regime 1―establishment density of 10,000 stems/ha with no thinning; Regime 2―establishment density of 10,000 stems/ha with a PCT of 7100 stems/ha at age 10 yr employing the maximum thinning response model; and Regime 3―establishment density of 10,000 stems/ha with a PCT of 7100 stems/ha at age 10 yr employing the minimum thinning response model. Denotations are defined in Figure 2(a) with the exception that diagonal isolines for mean dominant height range from a minimum of 6 m at the bottom of the graphic to a maximum of 22 m at the top of the graphic separated by 2 m increments.
Table 1. Contrasting rotational yield estimates for unthinned and precommercially thinned natural-origin jack pine and black spruce stands employing the maximum and minimum response models for an operational relevant crop plan using the revised SSDMMs.
aMerchantable volume specifications: 2.59 m and 5.03 m pulp and sawlog length, respectively, 4 cm merchantable top, 10 cm and 14 cm minimum log diameter for pulp and saw logs, respectively. S and R refer to stud and randomized length mill processing configurations. See Newton (2012c) for a complete computational summary of these metrics; bCrop plan including treatment specifics and economic assumptions are given in the text.
Table 2. Contrasting rotational stand-level performance indices for unthinned and precommercially thinned natural-origin jack pine and black spruce stands employing the maximum and minimum response models for an operational relevant crop plan using the revised SSDMMs.
aMAVI, MABI and MACI denote mean annual merchantable volume, biomass and carbon increment, respectively. S and R refer to stud and randomized length mill configurations. See Newton (2012c) for a complete computational summary of these metrics; bCrop plan including treatment specifics and economic assumptions are given in the text.
In terms of performance measures (Table 2), differences indicated that the PCT stands were less productive in terms of volume (−21% and −28%; −2% and −10%), biomass (−11% and −15%; −6% and −12%), and carbon sequestration (−8% and −8%; −6% and −12%) but much greater in terms of the proportion of usable end-prod- ucts produced (saw logs (increases of 16% and 12% over the control; increases of 26% and 16% over the control) and lumber volumes irrespective of processing configuration (increases of 7% and 6% over the control; increases of 5% and 4% over the control), and were more structurally stable. Thinned stands had slightly inferior fibre attributes (large branch size) and took longer to attain crown closure status. However, PCT substantially reduced the time required to attain operability status (−9 and −4 yr; −10 and −7 yr).
Although these differentials are due to the reduction in intraspecific competition and overall density-stress levels arising from the thinning treatments, the increase in actual site productivity as predicted by the response models, accelerated the rate of stand development. This enabled the thinned stands to reach a greater stage of development by rotation. Similarly, comparing the PCT treatments among themselves, indicated that the regimes employing the maximum response models (Regime 2) produced greater yields of slightly higher value and obtained operability status earlier than the regimes employing the minimum response models (Regime 3; Table 1 and Table 2). These differences are due to increased rate of stand development arising from a greater temporary increase in site quality: mean dominant height (m) of 18.0 for the regime using the maximum model versus 17.2 for the regime using the minimum model at a breast-height age 50 yrs for jack pine, and similarly 17.8 versus 17.2 for black spruce. The stand development pathways and associated rotational yield outcomes generated from these example simulations are consistent with expectation.
In order to assess the revised SSDMMs across a wide range of site qualities, initial densities, thinning treatments and rotation ages, a secondary evaluation was carried out. This evaluation consisted of assessing the models on their biological and empirical realism employing Bakuzis graphical matrices (sensu Leary 1997 ). Based on results derived from nested simulations for each response type and species involving 5 site classes (11 - 19 m by 2 m intervals), 5 rotational lengths (80 to 120 yr by 10 yr intervals) and 8 initial densities (3000 to 10,000 stems/ha by 1000 stems/ha intervals) and with and without precommercial thinning treatments (reducing densities to approximately to 2500 stems at age 10 yr), indicated that the predictions from the thinning response models were not contrary to expectation. Specifically, there was no evidence of consequential departures from expectation in terms of accepted stand dynamical theoretical constructs (e.g., Sukatschew’s effect, Eichhorm’s rule, self-thinning theory and yield-density relationships (see Newton, 2015c ) for additional details)).
3.3. Modelling Approach and Context
The underlying core models of the SSDMMs were constructed using a number of stand-type-specific functional and empirical quantitative relationships which collectively represent the cumulative effect of various underlying competition processes on individual tree attributes, size distributions and stand-level yields. These included the reciprocal equations of the competition-density (C-D) and yield-density (Y-D) effect (Kira et al., 1953; Shinozaki & Kira, 1956) , self-thinning rule (Yoda et al., 1963; Newton, 2006b) , composite height-diameter, taper, biomass, product and value equations (e.g., Newton and Amponsah, 2007 ), and parameter prediction equation systems (e.g., Newton and Amponsah, 2005 ). The site-based mean dominant height-age functions which largely govern the rate of stand development within these models, is the logical entry point for incorporating temporal developmental effects arising from silvicultural interventions. For example, in this study, the effect of accelerated stand development arising from PCT treatments was modelled employing an empirical-based adjustment to the site-based height-age functions. Depending on the thinning intensity (number of trees/ha removed) and type of response model variant chosen (minimum or maximum), the adjustment resulted in a percentage increase in the mean dominant height. This increase initialized at the conclusion of the response delay period, maximized at age 40 yr and then temporally dissipated until rotation according to the empirically-calibrated juvenile age- mature age correlation model.
In terms of the response modelling methodologies, Weiskittel et al. (2011) classified the various tree and stand modelling approaches commonly employed to quantify silviculture treatment effects into 3 general classes: 1) specification and parameterization of multiple treatment-specific response functions (e.g., development of separate growth models for treated and untreated stands); 2) specification of a single multivariate model where silvicultural treatment variables are explicitly accounted for in the model specification; and 3) modifying existing untreated prediction models via the addition of rate parameter modifiers in order to reflect changed temporal dynamics arising from the silvicultural treatment effects. Thus the approach utilized in this study belongs in the third class and focuses on modifying the principal temporal relationship responsible for driving stand development within the SSDMMs: i.e., the site-specific mean dominant height-age function. This approach is conceptually similar to the method utilized by 1) Newton (2003) for assessing genetic worth effects for conifers in central and eastern Canada; 2) Xie and Yanchuk (2003) in terms of integrating genetic worth effects within the growth and yield simulators developed for use in managing conifers in western Canada; and 3) quantifying responses to other silvicultural treatments including N-based forest fertilization (Newton and Amponsah, 2007) and chemical and mechanical vegetative management control (Newton, 2012d) . Although these approaches differ in regards to the assumptions of the type, duration and magnitude of the responses, they all share an essential commonality: i.e., they all incorporate rate modifiers into the site-specific height-age functions to account for the silvicultural treatment effect.
3.4. Concluding Notes
One of the principal uses of density management decision support systems, such as SSDMMs, is to determine the optimal crop plan for minimizing the time to operability status within natural-origin stands by comparing yield outcomes of density-stressed control stands against those from precommercial thinned stands. Consequently, the models presented in this study which explicitly account for density-dependent height release effects through adjustments to stand development rates, should improve the precision of yield forecasts and resultant density management decisions. As demonstrated in this study, model development is an iterative process in which amendments are commonly used to improve model performance as new knowledge is gained. As such, the new response models presented in this study should improve the conceptual basis and empirical predictive ability of density management models, and more generally, provide the modeling community with an alternative approach for quantifying responses to density management treatments.
References
- Ando, T. (1962). Growth Analysis on the Natural Stands of Japanese Red Pine (Pinus densiflora Sieb. et. Zucc.). II. Analysis of Stand Density and Growth (In Japanese; English Summary). Government of Japan, Bulletin of the Government Forest Experiment Station (Tokyo, Japan) No. 147, 1-77.
- Baldwin, Jr., V. C., Peterson, K. D., Clark, A., Ferguson, R. B., Strub, M. R., & Bower, D. R. (2000). The Effects of Spacing and Thinning on Stand and Tree Characteristics of 38-Year-Old Loblolly Pine. Forest Ecology and Management, 137, 91- 102. http://dx.doi.org/10.1016/S0378-1127(99)00340-0
- Carmean, W. H., Hazenberg, G., & Deschamps, K. C. (2006). Polymorphic Site Index Curves for Black Spruce and Trembling Aspen in Northwest Ontario. Forestry Chronicle, 82, 231-242. http://dx.doi.org/10.5558/tfc82231-2
- Carmean, W. H., Niznowski, G. P., & Hazenberg, G. (2001). Polymorphic Site Index Curves for Jack Pine in Northern Ontario. Forestry Chronicle, 77, 141-150. http://dx.doi.org/10.5558/tfc77141-1
- Drew, T. J., & Flewelling, J. W. (1979). Stand Density Management: An Alternative Approach and Its Application to Douglas-Fir Plantations. Forest Science, 25, 518-532.
- García, O. (2012). Self-Thinning Limits in Two and Three Dimensions. Mathematical and Computational Forestry & Natural Resource Sciences, 4, 66-72.
- Gómez-Vázquez, I., Fernandes, P. M., Arias-Rodil, M., Barrio-Anta, M., & Castedo-Dorado, F. (2014). Using Density Management Diagrams to Assess Crown Fire Potential in Pinus pinaster Ait. Stands. Annals of Forest Science, 71, 473- 484. http://dx.doi.org/10.1007/s13595-013-0350-4
- Kira T., Ogawa, H., & Sakazaki, N. (1953). Intraspecific Competition among Higher Plants. I. Competition-Yield-Density Interrelationship in Regularly Dispersed Populations. Journal of the Institute of Polytechnics, Series D4, 1-16.
- Lambeth, C. M. (1980). Juvenile-Mature Correlations in Pincaceae and Implications for Early Selection. Forest Science, 26, 571-580.
- Leary, R. A. (1997). Testing Models of Unthinned Red Pine Plantation Dynamics Using a Modified Bakuzis Matrix of Stand Properties. Ecological Modelling, 98, 35-46. http://dx.doi.org/10.1016/S0304-3800(96)01935-7
- McKinnon, L. M., Kayahara, G. J., & White, R. G. (2006). Biological Framework for Commercial Thinning Even-Aged Single-Species Stands of Jack Pine, White Spruce, and Black Spruce in Ontario. Northeast Science and Information Section: Ontario Ministry of Natural Resources, Report TR-046.
- Nelder, J. A. (1962). New Kinds of Systematic Designs for Spacing Experiments. Biometrics, 18, 283-307. http://dx.doi.org/10.2307/2527473
- Newton, P. F. (2003). Systematic Review of Yield Responses of Four North American Conifers to Forest Tree Improvement Practices. Forest Ecology and Management, 172, 29-51. http://dx.doi.org/10.1016/S0378-1127(02)00327-4
- Newton, P. F. (2004). Meta-Analytical Trends in Diameter Response of Black Spruce and Jack Pine to Pre-Commercial Thinning. In C. J. Cieszewski, & M. Strub (Eds.), Proceedings of the 2nd International Conference on Forest Measurements and Quantitative Methods and Management and the 2004 Southern Mensurationists Meeting (pp. 217-221). Athens, GA: Warnell School of Forestry and Natural Resources, University of Georgia.
- Newton, P. F. (2006a). Forest Production Model for Upland Black Spruce Stands―Optimal Site Occupancy Levels for Maximizing Net Production. Ecological Modelling, 190, 190-204. http://dx.doi.org/10.1016/j.ecolmodel.2005.02.022
- Newton, P. F. (2006b). Asymptotic Size-Density Relationships within Self-Thinning Black Spruce and Jack Pine Stand- Types: Parameter Estimation and Model Reformulations. Forest Ecology and Management, 226, 49-59. http://dx.doi.org/10.1016/j.foreco.2006.01.023
- Newton, P. F. (1997). Algorithmic Versions of Black Spruce Stand Density Management Diagrams. Forestry Chronicle, 73, 257-265. http://dx.doi.org/10.5558/tfc73257-2
- Newton, P. F. (2009). Development of an Integrated Decision-Support Model for Density Management within Jack Pine Stand-Types. Ecological Modelling, 220, 3301-3324. http://dx.doi.org/10.1016/j.ecolmodel.2009.07.025
- Newton, P. F. (2012c). A Decision-Support System for Density Management within Upland Black Spruce Stand-Types. Environmental Modelling and Software, 35, 171-187. http://dx.doi.org/10.1016/j.envsoft.2012.02.019
- Newton, P. F. (2012d). Yield Responses of Black Spruce to Forest Vegetation Management Treatments: Initial Responses and Rotational Projections. International Journal of Forestry Research, 2, 1-15. http://dx.doi.org/10.1155/2012/150157
- Newton, P. F. (2015a). Genetic Worth Effect Models for Boreal Conifers and Their Utility When Integrated into Density Management Decision-Support Systems. Open Journal of Forestry, 5, 105-115. http://dx.doi.org/10.4236/ojf.2015.51011
- Newton, P. F. (2015b). Density-Dependent Height Repression in Jack Pine and Black Spruce. (In Preparation)
- Newton, P. F. (2015c). Evaluating the Ecological Integrity of Structural Stand Density Management Models Developed for Boreal Conifers. Forests, 6, 992-1030. http://dx.doi.org/10.3390/f6040992
- Newton, P. F., & Amponsah, I. G. (2005). Evaluation of Weibull-Based Parameter Prediction Equation Systems for Black Spruce and Jack Pine Stand Types within the Context of Developing Structural Stand Density Management Diagrams. Canadian Journal of Forest Research, 35, 2996-3010. http://dx.doi.org/10.1139/x05-216
- Newton, P. F., & Amponsah, I. G. (2007). Comparative Evaluation of Five Height-Diameter Models Developed for Black Spruce and Jack Pine Stand-Types in Terms of Goodness-of-Fit, Lack-of-Fit and Predictive Ability. Forest Ecology and Management, 247, 149-166. http://dx.doi.org/10.1016/j.foreco.2007.04.029
- Newton, P. F., & Jolliffe, P. A. (1998). Assessing Processes of Intraspecific Competition within Spatially Heterogeneous Density-Stressed Black Spruce Stands. Canadian Journal of Forest Research, 28, 259-275. http://dx.doi.org/10.1139/x97-192
- Newton, P. F., & Weetman, G. F. (1993). Stand Density Management Diagrams and Their Utility in Black Spruce Management. Forestry Chronicle, 69, 421-430. http://dx.doi.org/10.5558/tfc69421-4
- Newton, P. F., & Weetman, G. F. (1994). Stand Density Management Diagram for Managed Black Spruce Stands. Forestry Chronicle, 70, 65-74. http://dx.doi.org/10.5558/tfc70065-1
- Newton, P. F., Lei, Y., & Zhang, S. Y. (2004). A Parameter Recovery Model for Estimating Black Spruce Diameter Distributions within the Context of a Stand Density Management Diagram. Forestry Chronicle, 80, 349-358. http://dx.doi.org/10.5558/tfc80349-3
- Newton, P. F., Lei, Y., & Zhang, S. Y. (2005). Stand-Level Diameter Distribution Yield Model for Black Spruce Plantations. Forest Ecology and Management, 209, 181-192. http://dx.doi.org/10.1016/j.foreco.2005.01.020
- Penner, M., Swift, D. E., Gagnon, R., & Brissette, J. (2006). A Stand Density Management Diagram for Balsam Fir in New Brunswick. Forestry Chronicle, 82, 700-711. http://dx.doi.org/10.5558/tfc82700-5
- Rowe, J. S. (1972). Forest Regions of Canada. Ottawa, Ontario: Government of Canada, Department of Environment, Canadian Forestry Service, Publication No. 1300.
- Shinozaki, K., & Kira, T. (1956). Intraspecific Competition among Higher Plants. VII. Logistic Theory of the C-D Effect. Journal of the Institute of Polytechnics: Series D, 12, 69-82.
- Sturtevant, B. R., Bissonette, J. A., & Long, J. N. (1996). Temporal and Spatial Dynamics of Boreal Forest Structure in Western Newfoundland: Silvicultural Implications for Marten Habitat Management. Forest Ecology and Management, 87, 313-325. http://dx.doi.org/10.1016/S0378-1127(96)03837-6
- Weiskittel, A. R., Hann, D. W., Kershaw Jr., J. A., & Vanclay, J. K. (2011). Forest Growth and Yield Modeling. Oxford: John Wiley & Sons. http://dx.doi.org/10.1002/9781119998518
- Xie, C. Y., & Yanchuk, A. D. (2003). Breeding Values of Parental Trees, Genetic Worth of Seed Orchard Seedlots, and Yields of Improved Stocks in British Columbia. Western Journal of Applied Forestry, 18, 88-100.
- Yoda, K., Kira, T., Ogawa, H., & Hozumi, K. (1963). Self-Thinning in Overcrowded Pure Stands under Cultivated and Natural Conditions. Journal of Biology, 14, 107-129.





