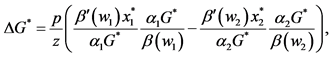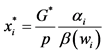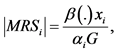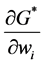Theoretical Economics Letters
Vol.06 No.03(2016), Article ID:67089,10 pages
10.4236/tel.2016.63049
Voluntary Contribution to Public Goods: Preferences and Wealth
Oskar Nupia
Department of Economics, Universidad de los Andes, Bogotá, Colombia

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 April 2016; accepted 31 May 2016; published 3 June 2016
ABSTRACT
This paper analyzes the role of wealth and its distribution in a model of voluntary-contribution to public goods where individuals’ preferences for these goods depend on the level of individual’s wealth. We find that under such circumstances a small redistribution of wealth among contributors is not necessary neutral. We then discuss the conditions under which a redistribution of wealth might improve efficiency in the aggregate provision of public goods. Unlikely what common sense might suggest, we show that a redistribution of wealth can increase the private provision of public goods regardless of whether individuals’ valuations for these goods increase or decrease as their level of wealth increases. Furthermore, we show that under some circumstances, a regressive redistribution of wealth can increase the provision of public goods.
Keywords:
Public Goods, Private Provision, Neutrality, Income Distribution

1. Introduction
We analyze in this paper the role of wealth and its distribution in a model of voluntary-contribution to pure public goods where individual’s preferences for these goods not only are determined by the respective level of individual’s wealth, but also are affected by changes in this wealth. Our positive analysis is motivated by the following observation. It is common in the literature on public goods to consider that individuals’ preferences (valuation) for these goods might be determined by the level of wealth (we discuss this literature below). Nevertheless, when considering this possibility, this literature has inexplicably assumed that changes in individual wealth do not affect individual’s preferences for the said goods. From our point of view, this is a clear theoretical inconsistency that might lead to misleading analysis results. In this study, we take into account this consideration into the standard mechanism of voluntary-contribution to public goods and find some novel results. Besides offering a proper analysis of the private provision of public goods under wealth dependent preferences, our analysis is of interest because, as we discuss below, there are several cases in which individual valuation for public goods can be affected by their level of wealth.
In our framework, pure public goods are defined in the usual way: goods that are non-rival (consumption of the good by one person does not reduce the consumption available to another person) and non-excludable (once the good has been provided to one consumer, it is not possible to prevent other people from consuming it). The manner in which we introduce our observation (i.e., that individual’s preferences for pure public goods depend on the respective level of individual’s wealth) into the model of voluntary-contribution to public goods is through the individual marginal rate of substitution (MRS) between the consumption of a private good and the consumption of a public good. More precisely, we assume that the (absolute value of each) individual’s MRS is a function of his or her level of wealth.
Three main and novel findings are obtained from our analysis. First, a small redistribution of wealth among contributors is not necessary neutral.1 Second, unlikely what common sense might suggest, a redistribution of wealth from a richer contributor to a poorer contributor can increase the private provision of public goods regardless of whether individuals’ valuation for these goods increase or decrease as their level of wealth increases. Third, under some circumstances, a small redistribution of wealth from a poorer contributor to a richer contributor can increase the provision of public goods. We characterize the conditions under which each of these possibilities occurs.
By considering a variety of circumstances, several authors have analyzed the role of wealth and its distribution in a voluntary-contribution mechanism to public goods.2 No one has analyzed (properly) this under wealth dependent preferences. Furthermore, our results differ from previous results in the literature under situations that can be apparently similar to our case of study. For instance, [11] studied the effect of a redistribution of wealth on the final provision of public goods when the marginal cost of providing these goods varies across contributors. In this context, they find that a transfer from a contributor with a high marginal cost to a contributor with a low marginal cost always increases equilibrium provision.
The remainder of this paper is organized as follows. In Section 2, we motivate in more detail both our main assumption and our analysis. Section 3 presents a simple example to illustrate our main point, and Section 4 develops a general framework and presents the main results. Section 5 concludes.
2. Wealth and Preferences for Public Goods
As said above, it is common in the literature on public goods to consider that individuals’ preferences for these goods might be determined by the level of wealth. There are several examples of this. For instance, the so-called income segregation hypothesis rests on the assumption that richer households value public goods less than poorer households [12] - [14] . The opposite has been assumed by [15] in their analysis of rent-seeking for pure public goods (see pp. 54). Furthermore, literature on private provision of public goods has also considered the possibility of differences in individual’s preferences caused by differences in individuals’ levels of wealth and, more generally, differences in individuals’ tastes (for instances, see [1] [16] , pp. 163-170).3
Nevertheless, although this literature has admitted that individuals’ preferences for public goods might be determined by the level of individuals’ wealth, this has inexplicably assumed that changes in individual wealth do not affect individual’s preferences for the said goods. Does it make any sense? From our point of view, this is a clear theoretical inconsistency. If one consider that individuals’ preferences for certain types of public goods are determined by their level of wealth, then it must be true that changes in the level of individuals’ wealth must affect said individuals’ preferences.
Besides this theoretical inconsistency in the literature, there are several cases in which individual valuation for public goods can be affected by their level of wealth. Firstly, consider environmental quality. Richer individuals may value their health and the health of their children more than poorer individuals, because the opportunity cost of getting sick or taking care of their children is greater for them. Since environmental quality might importantly affect individual health, richer individuals’ valuation of environmental quality should also be greater than that of poorer individuals. Additionally, changes in individual wealth should affect this valuation.
There is sufficient evidence demonstrating that individuals’ marginal willingness to pay for environmental goods increases as individual wealth increases [19] - [23] . Although it is difficult to know from these estimations whether differences in the marginal willingness to pay for such goods are due to differences in preferences, in the budget constraint or both, more recent empirical analyses directly suggest that individuals’ MRSs between private goods and environmental quality change as individuals level of wealth changes [24] [25] . In particular, these studies find that richer individuals are able to substitute a greater amount of private goods for a given increment in environmental quality than poorer individuals.
Another case in which individuals’ valuations of a public good may also increase with the level of wealth is public safety. Since richer individuals are more attractive to criminals than poorer ones, the former may value neighborhood public safety more than the latter. Using survey information for Brazil’s neighborhoods, [26] compute that a household’s concern for public safety increases as its level of wealth increases. Although they relate this result to a strong income effect, they also claim that it can be partly explained by increments in the marginal utility of public safety as a household’s wealth increases.
One can also think of cases where the valuation of public goods may be negatively correlated with the level of wealth. For instance, it may be that richer individuals place less value on public parks, inasmuch as they have access to private (excludible) spaces with similar characteristics; poorer individuals, on the other hand, may value public parks more, as they do not have access to such spaces. In this case, an individual’s valuation of the public good increases as the individual’s wealth decreases. Unfortunately, as far as we know, no evidence to this effect is currently available.
3. An Example: Log-Linear Preferences
To illustrate both how individuals’ preferences can be affected by the level of wealth, and how wealth and its distribution affect the final provision of public goods in a voluntary-contribution mechanism, we begin our analysis with a simple example in which individuals have log-linear preferences. Let us assume that there are two individuals ( ) who are interested in producing a public good. Each individual has to decide how to allocate his or her wealth (
) who are interested in producing a public good. Each individual has to decide how to allocate his or her wealth (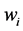 ) between the consumption of a private good (
) between the consumption of a private good ( ), and his or her contribution (
), and his or her contribution (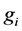 ) to the production of a public good. Thus, the individual budget constraint of each individual is given as
) to the production of a public good. Thus, the individual budget constraint of each individual is given as , where p is the relative price of the private good. The public good is produced using standard technology
, where p is the relative price of the private good. The public good is produced using standard technology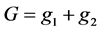 , where G is the total amount of the public good produced. Each individual decides independently and simultaneously how much money to contribute to the production of the public good. Without loss of generality, through this example, we assume that
, where G is the total amount of the public good produced. Each individual decides independently and simultaneously how much money to contribute to the production of the public good. Without loss of generality, through this example, we assume that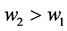 .
.
The new assumption we introduce into this framework is the following: preference intensities of individuals 1 and 2 for the public good depend on their respective levels of wealth. Therefore, the log-linear utility function for each individual can be represented as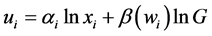 , where, for simplicity,
, where, for simplicity, 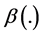 is assumed to be a continuous monotone function of that individual’s level of wealth. Therefore, if
is assumed to be a continuous monotone function of that individual’s level of wealth. Therefore, if 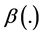 is an increasing function of wealth, the individual i’s valuation of the public good increases as his level of wealth in-
is an increasing function of wealth, the individual i’s valuation of the public good increases as his level of wealth in-
creases. The opposite happens if 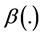 is a decreasing function of wealth. Notice that, under these circumstances, the absolute value of the individual’s
is a decreasing function of wealth. Notice that, under these circumstances, the absolute value of the individual’s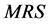 , given by
, given by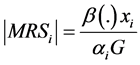 , is also a function of the indi-
, is also a function of the indi-
vidual’s respective level of wealth. Hence, if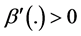 ,
, 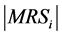 increases as increases. The opposite happens if
increases as increases. The opposite happens if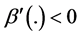
Each individual simultaneously chooses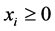
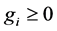
ual as given. In an interior solution, the required Nash equilibrium condition for each i is given by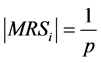
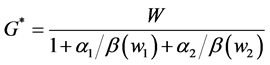
where 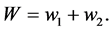
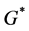
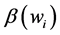
Equation (1) shows the difference between properly and improperly considering the wealth dependent preferences assumption in a voluntary-contribution mechanism. As said before, in the standard analysis this is common to assume that the valuation of the richer individual is larger (or smaller) than the valuation of the poorer individual, but, that these valuations are not affected by changes in individuals’ levels of wealth. In other words,
in this analysis 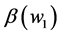
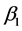
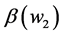
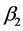
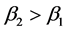
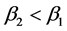
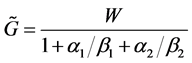
We can use Equation (1) to study the effect of changes in an individual’s wealth on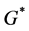
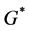
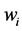
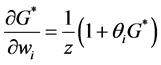
where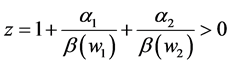
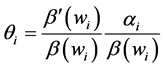
(multiplied by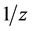
good production (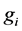

change as his level of wealth changes. 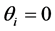

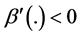
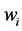
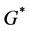
We can use Equation (2) to study how a redistribution of wealth between individuals 1 and 2 affects the final provision of G. Let us consider a small progressive redistribution of wealth―i.e., a redistribution of wealth from individual 2 (the richer individual) to individual 1 (the poorer individual), with W remaining unchanged, and both individuals still contributing a positive amount of resources to the public good after redistribution. The final
effect of this redistribution on the total provision of public good is given by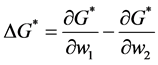
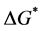
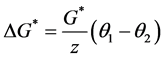
Since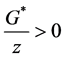
pends on the sign of the expression in parentheses in Equation (3). There are two terms involved in
term, 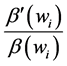
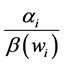
The larger this term―i.e., the more important i’s initial spending on the private good―the greater will be the impact of a change in i’s preference intensity for the public good on the aggregate provision of G. Thus, the effect of a redistribution of wealth on the final provision of G depends not only on how individuals’ preferences for a public good change as their respective levels of wealth change, but also on how important their respective spending on the private good is prior to the redistribution.5 Once again, if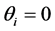
To fix ideas on how a redistribution of wealth can affect the level of G, let us assume that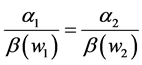
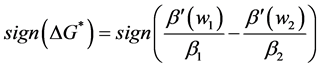
The effect of a redistribution of wealth on G now depends exclusively on the difference between changes in the respective individuals’ intensity preferences for the public good as 
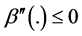
not enough to obtain this result. If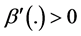
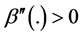
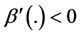
The example in this section illustrates both how individuals’ preferences are affected by individuals’ levels of wealth when one consistently consider this possibility, and how wealth and its distribution affect the final provision of public goods in a voluntary-contribution mechanism. In the next section, we generalize these findings.
4. A General Framework
Consider the general model for the private provision of public goods, wherein there is one public good (G), one private good (x) and n consumers. Same as before, each consumer i decides how to allocate his or her total exogenous wealth (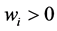
lic good (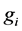
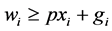

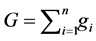
We assume that individual preferences are affected by respective levels of individual wealth. More precisely, we assume that the absolute value of each individual’s 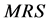
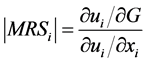

If richer individuals value G more than poorer individuals, then function 

on this case because, as we mentioned in Section 2, this seems to be the more likely situation for certain public goods. However, our analysis can be extended to analyze the case where 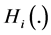
Under the conditions described above, each of n individuals simultaneously chose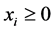
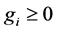
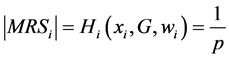
Equation (6) implicitly defines each contributor’s best response contribution to the public good. For non-con- tributors, the best response is zero contribution to the public good.8 We denote by C the set of contributors, and by 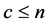
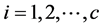
Assuming that the conditions of the implicit function theorem are satisfied, it follows from Equation (6) that for each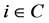
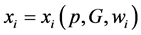
Plugging Equation (7) into the individual budget constraint and summing up over those i’s ∈ C, we get:

Let
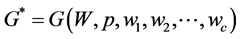
Equation (9) represents aggregate private provision of the public good in this economy. Since for a given vector of individuals’ respective wealth, 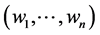
same as his maximization problem in the standard model of the private provision of public goods, the existence of an equilibrium in our framework is already a well-known result (see [2] ).
4.1. Changes in Wealth
We begin by analyzing how changes in a contributor’s level of wealth affect the private provision of
Proposition 1. Assume that

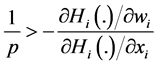
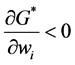
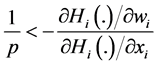
Proof. Applying implicit differentiation to Equation (8), for any contributor i, we get that, 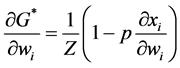
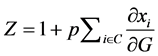
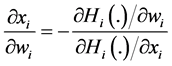
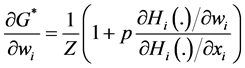
It also follows from Equation (6) that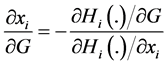
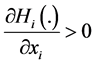
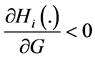

depends on the sign of the right-hand term in the parentheses of Equation 10. The result in Proposition 1 follows from the sign of this term. QED
Result in Proposition 1 states how the aggregate provision of G changes as contributor i’s wealth changes. Equation (10) involves both the standard wealth effect, measured by (1/Z), and a new effect given by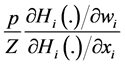
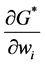
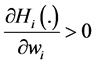

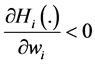
Proposition 1 raises the possibility that the public good in our framework can be an inferior good. When this is the case, although equilibrium existence is guaranteed (see [2] ), uniqueness is not (see [9] for some examples). In this context, uniqueness means that there is a unique Nash equilibrium (i.e. a unique vector of contributions) with a unique quantity of public good and a unique set of contributors. The existence of multiple equilibria makes it difficult to analyze how any redistribution of wealth affects the provision of public good in our framework. For this reason―and similar to [1] and [2] (see Theorem 1, pp. 29)―in what follows, we concentrate on analyzing the effect of small redistributions of wealth (i.e., those redistributions that only involve contributors and that do not affect the set of contributors) on the aggregate provision of G.
4.2. Changes in the Distribution of Wealth
Let us now study how a small redistribution of wealth affects the aggregate provision of G in our framework. We state this result in Proposition 2.
Proposition 2. Let us consider contributors 1 and 2 with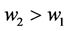
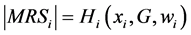
a) A small redistribution of wealth, either progressive (from 2 to 1) or regressive (from 1 to 2) is not neutral if and only if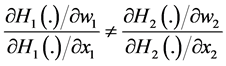
b) If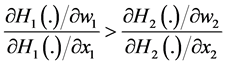
c) If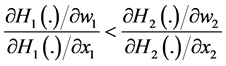
Proof. Consider contributors 1 and 2 with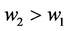
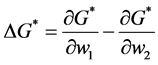
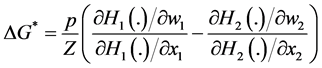
If the redistribution is regressive, then the change in G is given
Proposition 2(a) states the condition under which a small redistribution of wealth in not neutral. Clearly, this redistribution is neutral if, as it has been assumed in previous literature,
under the same implicit conditions that the standard model of the private provision of public goods imposes on individuals’ behavior. As [2] claim, in the standard framework, after a redistribution of wealth between contributors, each individual consumes exactly the same amount of the private good that he did prior to the redistribution. In other words, the standard model implicitly imposes the condition that when there is a redistribution of
wealth, then 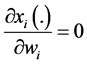
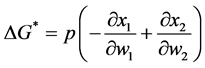
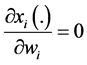
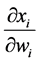
Results in Proposition 2(b) and 2(c) state the conditions under which a progressive/regressive redistribution of wealth among contributors increases/decreases the aggregate provision of G. This result depends on the sign of the right-hand term in parentheses in Equation (11). For each individual (1 and 2), this expression involves two
terms. The first term is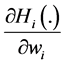
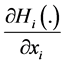
assumptions on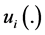
Therefore, results in Proposition 2(b) and 2(c) indicate that if the relative change in the individual’s preference intensity for public goods is larger for individual 1 (the poorer individual) than for individual 2 (the richer individual), then a redistribution of wealth from 2 to 1 always increases the final provision of G. When the opposite happens, a redistribution of wealth from 2 to 1 always decreases the final provision of G. In order to increases G in this case then, a regressive redistribution of wealth is required. Thus, our results allow us to anticipate which type of redistribution could be most useful for improving the efficiency of the aggregate provision of G.
Interestingly, to the extent that we assume that 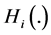

his or her respective level of wealth increases, it is possible to observe either an increment or a decrease in the final provision of G following a progressive redistribution of wealth. The same thing happens when an individual’s valuation for G decreases as his or her respective level of wealth increases. Notice that this holds even if we
assume that
in determining the final effect of a redistribution of wealth on G is how the magnitudes of the relative change in the individual’s preference intensity for public goods compares across those individuals involved in the redistribution of wealth.
As noted above, Equation (11) can be also used to study the effect on G of a redistribution of wealth when function 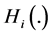

5. Conclusions
In this paper, we analyzed the role of wealth and its distribution in a model of voluntary-contribution to public goods when individuals’ preferences for these goods are affected by the respective level of individual wealth. We find that, under these conditions, a small redistribution of wealth among contributor is not necessary neutral and that, unlikely what common sense might suggest, redistributing wealth from a richer contributor to a poorer contributor can increase the private provision of public goods regardless of whether individuals’ valuations for these goods increase or decrease as their wealth increases. Furthermore, we show that under some circumstances, a small regressive redistribution of wealth (from a poor individual to a rich individual) might increase the provision of public goods.
Which type of wealth redistribution might be most useful in reducing the under-provision of public goods in our framework depends on how the relative change in individuals’ MRSs compares across individuals. This relative change is defined as the ratio between the change in the absolute value of the individual’s MRS as his or her level of wealth changes, and the change in the absolute value of the individual’s MRS as his or her private consumption changes. If this relative change in MRSs is greater for poorer individuals than for richer individuals, then a progressive redistribution of wealth will always increase the final provision of G. When the opposite happens, a regressive distribution of wealth is needed in order to increase the final provision of G.
Our analysis calls the attention on how to consider the assumption of wealth dependent preferences for public goods properly. Omitting that these preferences not only differ across individuals with different levels of wealth but also are affected by changes in these levels might lead to misleading analysis results. Finally, our results create space for public intervention for those public goods where individuals’ valuations are affected by their respective wealth. As mentioned in Section 2, there are several cases in which individual valuation for public goods can be affected by their level of wealth.
Acknowledgements
I thank Richard Cornes, Jorge Garcia, Pierre Pestieau and Julio Robledo for very useful comments on a previous version of this paper.
Cite this paper
Oskar Nupia, (2016) Voluntary Contribution to Public Goods: Preferences and Wealth. Theoretical Economics Letters,06,432-441. doi: 10.4236/tel.2016.63049
References
- 1. Warr, P. (1983) The Private Provision of a Public Good Is Independent on the Distribution of Income. Economic Letters, 13, 207-211.
http://dx.doi.org/10.1016/0165-1765(83)90087-3 - 2. Bergstrom, T., Blume, L. and Varian, H. (1986) On the Private Provision of Public Goods. Journal of Public Economics, 29, 25-49.
http://dx.doi.org/10.1016/0047-2727(86)90024-1 - 3. Cornes, R. and Sandler, T. (1994) The Comparative Static Properties of the Impure Public Good Model. Journal of Public Economics, 54, 403-421.
http://dx.doi.org/10.1016/0047-2727(94)90043-4 - 4. Andreoni, J. (1990) Altruism and Donations to Public Goods: A Theory of Warm-Glow Giving. The Economic Journal, 100, 464-477.
http://dx.doi.org/10.2307/2234133 - 5. Andreoni, J. (1988) Privately Provided Public Goods in a Large Economy: The Limits of Altruism. Journal of Public Economics, 35, 57-73.
http://dx.doi.org/10.1016/0047-2727(88)90061-8 - 6. Fries, T., Golding, E. and Romano, R. (1991) Private Provision of Public Goods and the Failure of the Neutrality Property in Large Finite Economies. International Economy Review, 32, 147-157.
http://dx.doi.org/10.2307/2526937 - 7. Sandler, T. and Posnett, J. (1991) The Private Provision of Public Goods: A Perspective of Neutrality. Public Finance Review, 19, 22-42.
http://dx.doi.org/10.1177/109114219101900102 - 8. Gradstein, M., Nitzan, S. and Slutsky, S. (1994) Neutrality and the Private Provision of Public Goods with Incomplete Information. Economics Letters, 46, 69-75.
http://dx.doi.org/10.1016/0165-1765(94)90079-5 - 9. Kerschbamer, R. and Puppe, C. (1998) Voluntary Contributions When the public Good Is Not Necessarily Normal. Journal of Economics, 68, 175-192.
http://dx.doi.org/10.1007/BF01237190 - 10. Ihori, T. (1996) International Public Goods and Contribution Productivity Differentials. Journal of Public Economics, 61, 139-154.
http://dx.doi.org/10.1016/0047-2727(95)01522-1 - 11. Cornes, R. and Hartley, R. (2007) Aggregative Public Good Games. Journal of Public Economic Theory, 9, 201-219.
http://dx.doi.org/10.1111/j.1467-9779.2007.00304.x - 12. Epple, D. and Sieg, H. (1999) Estimating Equilibrium Models of Local Jurisdictions. Journal of Political Economy, 107, 645-668.
http://dx.doi.org/10.1086/250074 - 13. Schmidheiny, K. (2006) Income Segregation and Local Progressive Taxation: Empirical Evidence from Switzerland. Journal of Public Economics, 90, 429-458.
http://dx.doi.org/10.1016/j.jpubeco.2005.09.003 - 14. Schaltegger, C., Somogyi, F. and Sturm, J. (2011) Tax Competition and Income Sorting: Evidence from Zurich Metropolitan Area. European Journal of Political Economy, 27, 455-470.
http://dx.doi.org/10.1016/j.ejpoleco.2011.01.004 - 15. Katz, E., Nitzan, S. and Rosenberg, J. (1990) Rent-Seeking for Pure Public Goods. Public Choice, 65, 49-60.
http://dx.doi.org/10.1007/BF00139290 - 16. Cornes, R. and Sandler, T. (1996) The Theory of Externalities, Public Goods and Club Good. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9781139174312 - 17. Kalman, P.J. (1968) Theory of Consumer Behavior When Prices Enter the Utility Function. Econometrica, 56, 497-510.
http://dx.doi.org/10.2307/1909519 - 18. Pollack, R.A. (1977) Price Dependent Preferences. The American Economic Review, 67, 64-75.
- 19. Kramer, R. and Mercer, D. (1997) Valuing a Global Environmental Good: U.S. Residents’ Willingness to Pay to Protect Tropical Rain Forests. Land Economics, 73, 196-210.
http://dx.doi.org/10.2307/3147282 - 20. Gürlük, S. (2006) The Estimation of Ecosystem Services’ Value in the Region of Misi Rural Development Project: Results from a Contingent Valuation Survey. Forest Policy and Economics, 9, 209-218.
http://dx.doi.org/10.1016/j.forpol.2005.07.007 - 21. Jim, C.Y. and Chen, W. (2006) Recreation-Amenity Use and Contingent Valuation of Urban Green Spaces in Guangzhou, China. Landscape and Urban Planning, 75, 81-96.
http://dx.doi.org/10.1016/j.landurbplan.2004.08.008 - 22. Treisman, T. and Gartner, J. (2006) Are Residents Willing to Pay for Their Community Forest? Results of a Contingent Valuation Survey in Missouri, USA. Urban Studies, 43, 1537-1547.
http://dx.doi.org/10.1080/00420980600749928 - 23. Wang, H. and Mullahy, J. (2006) Willingness to Pay for Reducing Fatal Risk by Improving Air Quality: A Contingent Valuation Study in Chongqing, China. Science of the Total Environment, 367, 50-57.
http://dx.doi.org/10.1016/j.scitotenv.2006.02.049 - 24. Levinson, A. (2009) Valuing Public Goods Using Happiness Data: The Case of Air Quality. NBER Working Papers Series No. 15156.
- 25. Luechinger, S. and Raschky, P.A. (2009) Valuing Flood Disasters Using the Life Satisfaction Approach. Journal of Public Economics, 93, 620-633.
http://dx.doi.org/10.1016/j.jpubeco.2008.10.003 - 26. Pradhan, M. and Ravallion, M. (2003) Who Wants Safer Streets? Explaining Concern for Public Safety in Brazil. Journal of Economic Psychology, 24, 17-33.
http://dx.doi.org/10.1016/S0167-4870(02)00152-6
NOTES
1A surprising result in the literature on the private provision of public goods is that a small redistribution of wealth among those individuals making a strictly positive contribution to the production of a public good does not have any effect on its aggregate provision―the so-called neutrality theorem [1] [2] . It has been claimed that this result holds true regardless of differences in individual preferences.
2These circumstances are: the presence of corner solutions [2] ; impure public goods [3] [4] ; large economies [5] [6] ; non-Nash behavior, such as the presence of nonzero conjectural variations [7] ; information asymmetries [8] ; inferior public goods [9] ; differences in the marginal cost of providing public goods [10] [11] .
3Other studies have also assumed that individuals’ preferences can be affected by some of the usual exogenous variables in a decision model. For instance, many studies have analyzed the demand for private goods when individuals’ preferences are affected by market prices. Pioneer studies in this field are [17] [18] .
4In equilibrium,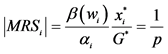
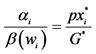
5There is another way to understand the two terms in parentheses in Equation (3). Actually, in the next section, we relate these terms to changes in the (absolute value of) the individual’s 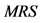
6This assumption implies several things. First of all, since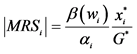
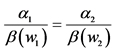


7Notice that function 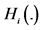
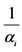
8An individual i is a contributor if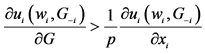
9Notice that Equation (3) in our example in Section 2 can be rewritten as