Theoretical Economics Letters
Vol.04 No.09(2014), Article ID:52091,2 pages
10.4236/tel.2014.49101
The Lerner Index and Economic Efficiency*
R. G. Chambers1, R. Färe2, S. Grosskopf2,3
1University of Maryland, College Park, USA
2Oregon State University, Corvallis, USA
3CERE, Umeå, Sweden
Email: rchambers@umd.edu, rolf.fare@orst.edu, Shawna.grosskopf@orst.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 October 2014; revised 10 November 2014; accepted 2 December 2014
ABSTRACT
This short paper brings together two literatures: the first is the Lerner Index as a measure of imperfect competition familiar from industrial organization and the second is a measure of performance from the efficiency literature, namely the Nerlovian indicator. We show how these may be related and the resulting decomposition of the Lerner index which results.
Keywords:
Lerner Index, Nerlovian Indicator, Profit Efficiency

In this short paper, we establish a relationship between the Lerner index―familiar from the industrial organi- zation literature―and the less well-known Nerlovian indicator of profit efficiency. We prove that the Lerner index is the first order derivative of the Nerlovian indicator.
We also show that the Lerner index can be decomposed into three components: i) cost elasticity, ii) Farrell output technical efficiency (Farrell, 1957) [1] and iii) return to the dollar (Georgescu-Roegen, 1951) [2] .
We begin with the Lerner index, which as Lerner put it, is the
“...formula that I wish to put forward as a measure of monopoly power. If 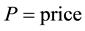 and
and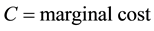 ,
,
then the index of the degree of monopoly power is ” Lerner (1934, p. 169) [3] .
” Lerner (1934, p. 169) [3] .
With respect to this index of monopoly power, Samuelson (1964, p. 173) [4] wrote
“Today this may seem simple, but I can testify that no one at Chicago or Harvard could tell me in 1935 why 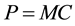 was a good thing, and I was a persistent Diagenes”.
was a good thing, and I was a persistent Diagenes”.
Turning to the Nerlovian indicator (Chambers, Chung and Färe, 1998) [5] ; it was introduced as a measure of profit efficiency, specifically it is the normalized difference between maximal profit and observed profit. It is dual to the shortage function (Luenberger, 1992) [6] , or equivalently to the directional technology distance function (Chambers, Chung and Färe, 1998) [5] .
To continue, let 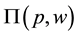 be a profit function, with input prices
be a profit function, with input prices  and output prices
and output prices . Denote observed profit by
. Denote observed profit by , the input and output directional vectors by
, the input and output directional vectors by 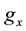 and
and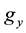 , respectively. The Nerlovian indicator is then defined as
, respectively. The Nerlovian indicator is then defined as
 (1)
(1)
In our case we assume that there is a single output and output price and that the cost minimization problem is solved so that 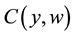 is a cost function. In addition we take
is a cost function. In addition we take 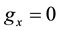 and
and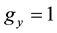 , then the Nerlovian indi- cator reads as
, then the Nerlovian indi- cator reads as
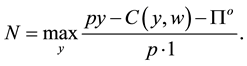 (2)
(2)
The first order condition is
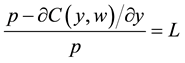 (3)
(3)
which is the Lerner Index.
In addition to showing that the Lerner index is the first order condition of the Nerlovian profit indicator we see that the index is normalized by the output price rather than the marginal cost.
Let us recall some basic notions from duality theory, specifically the duality between Shephard’s 1970 output distance function and the revenue function. We begin with technology; thus if

with 


and the corresponding revenue function is given by

The distance function may be retrieved from the revenue function by optimizing over 

From this duality it follows that

and thus

Note that 

Using (9) we may write the Lerner Index from (3) as
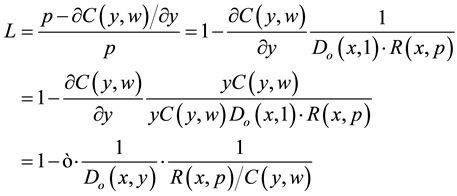
where:
・ 
・ 
・ 
Thus the Lerner Index may be deduced from a measure of profit efficiency―the Nerlovian Indicator―and may be decomposed into three further economic performance measures. We leave generalization to the multiple output case to future research.
References
- Farrell, M.J. (1957) The Measurement of Productive Efficiency. Journal of the Royal Statistical Society Series A, General, 120, 253-281. http://dx.doi.org/10.2307/2343100
- Georgescu-Roegen, N. (1951) The Aggregate Linear Production Function and Its Application to the Von Neumann Economic Model. In: Koopmans, T., Ed., Activity Analysis of Production and Allocation, Wiley, New York.
- Lerner, A.P. (1934) The Concept of Monopoly and the Measurement of Monopoly Power. The Review of Economic Studies, 1, 157-175. http://dx.doi.org/10.2307/2967480
- Samuelson, P.A. (1964) A.P. Lerner at Sixty. The Review of Economic Studies, 31, 169-178. http://dx.doi.org/10.2307/2295906
- Chambers, R.G., Chung, Y. and Färe, R. (1998) Profit, Directional Distance Functions, and Nerlovian Efficiency. Journal of Optimization Theory and Applications, 98, 351-364. http://dx.doi.org/10.1023/A:1022637501082
- Luenberger, D.G. (1992) New Optimality Principles for Economic Efficiency and Equilibrium. Journal of Optimization Theory and Applications, 75, 221-264. http://dx.doi.org/10.1007/BF00941466
NOTES
*We thank V. Tremblay for his comments on an earlier draft.
1See Färe and Primont (1994) for an exposition of Shephard’s duality theories.



