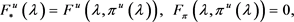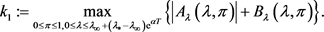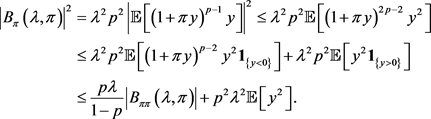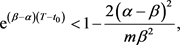Journal of Mathematical Finance
Vol.09 No.03(2019), Article ID:94453,23 pages
10.4236/jmf.2019.93020
Optimal Portfolio Choice in a Jump-Diffusion Model with Self-Exciting
Baojun Bian1, Xinfu Chen2, Xudong Zeng3
1Department of Mathematics, Tongji University, Shanghai, China
2Department of Mathematics, University of Pittsburgh, Pittsburgh, PA, USA
3School of Finance, Shanghai University of Finance and Economics, Shanghai, China
Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 25, 2019; Accepted: August 17, 2019; Published: August 20, 2019
ABSTRACT
We solve the optimal portfolio choice problem for an investor who can trade a risk-free asset and a risky asset. The investor faces both Brownian and jump risks and the jump is modeled by a Hawkes process so that occurrence of a jump in the risky asset price triggers more sequent jumps. We obtain the optimal portfolio by maximizing expectation of a constant relative risk aversion (CRRA) utility function of terminal wealth. The existence and uniqueness of a classical solution to the associated partial differential equation are proved, and the corresponding verification theorem is provided as well. Based on the theoretical results, we develop a numerical monotonic iteration algorithm and present an illustrative numerical example.
Keywords:
Portfolio Choice, Jump Diffusion, Stochastic Volatility, Hawkes Process, Self-Exciting Jump, HJB Equation

1. Introduction
Empirical studies suggest that asset price encounters jumps and its volatility is stochastic. Further studies show that jumps occur in clusters, that is, a sequence of jumps occur in short time following a (big) jump which occurs after a relatively long quiet period of time. The feature of clustered jumps can be caught by a type of stochastic process known as Hawkes process. In this paper, we model occurrence of jumps by a Hawkes process hence our model is an extension of well-known jump-diffusion models, e.g. [1] . Meanwhile, we assume that such Hawkes jumps may occur in asset price itself as well as in its volatility. As a result, our model merges with the vast literature of stochastic volatility.
The contributions of the present paper are twofold. First, we solve the optimal investment problem and prove a verification result for a CRRA utility while [2] solves for a logarithm utility function. They do discuss the CRRA case but leave proofs to some references. However, our work shows that it is highly non-trivial to prove the existence and uniqueness of a classic solution to the associated Hamilton-Jacobi-Bellman (HJB) equation, which is essential for solving the optimal portfolio choice problem and implementing numerical methods. Second, our model may incorporate stochastic volatility or stochastic risk premium. Thus it shall be powerful to explain more financial phenomena, e.g. flight-to-quality, under-diversification, and possibly disclose more economic insights.
Technically, in the strand of the relevant literature, [3] introduces an Ornstein-Uhlenbeck (OU) type process of subordinator to model volatility. After that, there are several works about optimal portfolio selection in a model with OU type processes of subordinators. For example, [4] solves the portfolio choice problem in a model where volatility is a linear combination of Ornstein-Uhlenbeck type processes of subordinators. [5] solves the optimal investment and consumption problem in a similar model where a state variable (economic factor) is an Ornstein-Uhlenbeck type process of subordinator. They deal with a more general model, compared to [4] . As a result, they arrive at a nonlinear partial integro-differential equation, instead of a linear one in the latter. In both of these two papers, there are no jump components in the dynamics of asset prices. In stark contrast to the literature we incorporate jumps in the asset price in the present paper and hence confront a new/different challenge (if not more difficult) when we solve the optimal portfolio choice problem.
In our general setting, the volatility is a function of the state variable (the jump intensity) following a Hawkes process. Hence the present paper may combine two strands of research: modeling volatility by an OU type of process of subordinator and modeling jumps by Hawkes processes together. There are several papers studying the case where there are jumps in volatilities, e.g. [5] , etc., while the present paper considers jumps in both of asset price and volatility, and in jump intensity as well. This leads to a more complicated HJB equation than in [5] . As a result, our model has the features of stochastic volatility and self-exciting, while the optimal investment problem is still solvable in sense of by an iteration method, given that the iteration is proved to converge correctly to the unique classical solution of the problem.
This paper is incremental to the few aforementioned papers and dedicated to solving several technical problems related to CRRA utility functions. Nevertheless, the literature on portfolio choice is vast and is growing quickly. We would like to refer to some of them, for example, [6] , which proposes a semivariance method for diversified portfolio selection; [7] , that discusses a portfolio adjusting problem. The both assume that security returns are subject to experts’ estimations.
The organization of the paper is as follows. We formulate our model and optimal portfolio choice problem in Section 2. The Hawkes process is introduced in this section. In Section 3, we analyze the HJB equation. The existence and uniqueness of a classical solution to the equation are proved under some appropriate conditions. We also prove a verification theorem for the solution in Section 4. Two illustrative examples and one numerical example are provided in Section 5. Conclusion and further discussion are in Section 6. An extension is supplied in Appendix.
2. Problem Formulation
2.1. Hawkes Process for Self-Exciting Jumps
A Hawkes process is a counting process with self-exciting feature. Roughly speaking, it is a compounded Poisson process with stochastic intensity.
Given a complete probability space , a counting process, , satisfies
where the intensity process is given by the integrated form
or by the differentiation form
(2.1)
here is the long-run average of the jump intensity corresponding to the jump; is the decay rate driving the jump intensity back to the long-run average before a jump occurs; is a constant indicating non-negative impact of the jump occurrence on the jump intensity.
A jump process with the jump intensity described by (2.1) is called a Hawkes process [8] . It is known that the process is stationary if . A Hawkes process differs from a doubly stochastic Poisson process since its increments are not independent. is not Markovian but is. The compensated process is a local martingale. For more information and a formal definition of Hawkes process, we refer to [8] . Figure 1 illustrates a sample path of one self-exciting (Hawkes) process.
The Hawkes process has a feature of self-exciting which is ideal to model jumps in financial markets. As one jump occurs, the jump intensity is increased by the occurred jump through the mechanics of (2.1). Hence a sequent jump happens more likely in a unit time following. In other words, as a jump happens, it impacts on the jump intensity as well as on itself. As a result, one may see a sequence of jumps in a short frame of time after one (big) jump. Thus, jump is self-triggered through the channel described by (2.1) and jumps tend to be clustered. Of course, it may not be the only channel to generate clustered jumps, but the empirical studies of [9] show an evidence that this channel is convincing.
Figure 1. A sample path of Hawkes and stock price .
Meanwhile, the mean-reversion property of (2.1) prevents the jump intensity from explosion given . Indeed, taking the expectation of (2.1) and using we obtain that
2.2. Asset Dynamics with Self-Exciting Jumps
We consider a market with a risk-free asset (bond) and a risky asset (stock). The price of the risk-free asset follows dynamics:
where r is the risk-free interest rate. The price of the risky asset follows a stochastic differential equation
(2.2)
where is a Hawkes process described in the preceding section, is a standard Brownian motion, and is a random jump size independent of the jump process and the Brownian motion. To be more precise, we define
where are i.i.d. random variables that are independent of either the Brownian motion or the jump process.
Note that the volatility and the risk premium are set to be functions of the jump intensity. Given appropriate conditions about the mappings (e.g. monotonic mappings), we may write and , so our model is compatible with many models studied in stochastic volatility literature.
2.3. Optimal Portfolio Selection Problem
Now we turn to the Merton’s problem: An investor invests in the risky asset and the risk-free asset in a time horizon . In order to maximize the expected utility of the terminal wealth, the investor needs to find an optimal investment strategy.
Let be the wealth of portfolio at time t and be the proportion of wealth invested into the risky asset at time t. Then
(2.3)
An investment strategy is an adapted stochastic process . It is admissible if the associated wealth process is non-negative almost surely. The jump size , in particular, is assumed to take a form of , where is a Gaussian random variable. This setting is popularly admitted in the literature of jump-diffusion model. See, for example, the seminal paper of [1] . As a result, an admissible strategy shall satisfy the constraint . Thus, shorting either stock or bond is not permitted. This constraint condition may be relaxed1 according to distribution and support set of a specific jump size . We denote all admissible strategies by .
An optimal investment strategy is a strategy that maximizes the expected utility of the terminal wealth. That is, the objective of an investor is to find V and such that
(2.4)
where is the expectation conditioned on and . In this paper, we solve the problem for the CRRA utility . We prove the existence and uniqueness of a classical solution to the associated HJB equation when . By a similar approach, our framework may be extended to the case of regardless of an amount of efforts. The case of logarithm utility (corresponding to ) has been studied in [2] while assuming constant volatility and risk premium. In Section 5, we will discuss an extension case of logarithm utility with stochastic volatility and stochastic risk premium, as an application of our general results.
The Hamilton-Jacobi-Bellman (HJB) equation associated with the above stochastic optimization problem can be derived as
(2.5)
(2.6)
1If a tight bound of Y is , where a and b are positive constants, then is admissible if and only if .
Here subscripts denote partial derivatives and Y is a random variable having the same distribution as . In this paper, we shall make a full mathematical analysis of the HJB Equation (2.5) subject to the terminal condition (2.6), and a certain growth condition such as (2.8) below.
There are several papers studying the case where there are jumps in volatilities, e.g. [5] . Different from only jumps in volatility, our model incorporates jumps in both of asset price and volatility, and in jump intensity as well. It is worth to mention that the HJB Equation (2.5) is more complicated than that in [5] . The framework of our model is the same as that in [2] , except the setting of utility function. As well-known, CRRA utility functions generally involve much more difficult technical problems than the logarithm utility function.
Remark 2.1. The HJB Equation (2.5), together with the terminal condition (2.6), may have several solutions. From a view point of partial differential equation, it is necessary to prescribe an asymptotic behavior of the solution as . Note that, as a suboptimal strategy, investing everything into the risk-free asset gives the lower bound
(2.7)
Although it is very had to estimate an upper bound, we shall prove the existence of a unique solution of (2.5)-(2.6) under the following growth condition: For some constant .
(2.8)
3. Mathematical Analysis of the HJB Equation
3.1. Scaling Invariance
Note that applying the same strategy for two initial portfolios with initial condition and respectively, we find that the corresponding wealth of the two portfolios differ by a factor of x at any time . Hence, optimal strategies do not depend on x, and we have the scaling invariance
(3.1)
where is the time to expiry and . Plugging (3.1) into (2.5) and using Remark 2.2 we obtain the equation for H:
(3.2)
(3.3)
where
(3.4)
2We assume that the optimizer is achieved in the interior.
It is easy to check that both A and B are concave function of . Hence, if , then there exists a unique such that2
(3.5)
In fact, with integrability of the jump size Y the first order condition brings us that
(3.6)
The second term in the right hand side of the above formula is the hedging demand for the self-exciting jump risks.
In the rest of this section, we shall impose certain conditions on and Y and show that the HJB Equation (3.2) subject to the initial condition (3.3) and a certain growth condition admits a unique solution. In the next section we prove a verification result showing that the solution obtained solves the optimal investment problem.
For the case of CRRA utility, [2] suggest to prove the existence of a solution by verifying a contracting mapping as [5] . Our attempts show that it is not a trivial task to do that, instead, we use a different analytic method to accomplish the mission.
3.2. Basic Assumptions
First of all, we state some necessary assumptions as follow.
(3.7)
Recall that we assume . Thus a.s., .
To explain our idea in a clear manner, we assume that
(3.8)
Intuitively, the assumption (3.8) claims that the excess return of the asset will be negative if the jump frequency is high enough. In the literature of jump-diffusion models, the excess return is usually assumed with a compensation of jump risk, see, e.g. [10] . Hence the assumption (3.8) is equivalent to say that may not be enough compensated when (negative) jumps occur at a high frequency. That does not sound unreasonable.
The assumption may be relaxed to
(3.9)
We shall discuss this later in the Appendix.
Under (3.8) we define
(3.10)
3.3. An Integral Formulation
Let . We study the problem
(3.11)
where, with A and B as in (3.4), is a non-local operator defined by
Note that satisfies, for any positive constant c and continuous functions u and v,
(3.12)
We shall use characteristic curves to convert (3.11) into an equivalent integral formulation. For this we introduce
(3.13)
For notational simplicity, in the sequel, we write simply as .
Let M be a positive constant to be determined. For fixed and along the characteristic curve , we obtain from (3.11) that
Integration over gives
Substituting the definition of into the expression we obtain the integral formulation:
(3.14)
for every where D and are as in (3.13).
In the sequel we shall choose an appropriate positive constant M and solve the above integral equation by a monotonic iteration technique.
3.4. Determination of the Constant M
First we consider the function
Direct calculation yields
Hence, we have the following:
Lemma 1. For each , there exists a unique such that
(3.15)
In addition, the following holds:
1) If , then and ;
2) If , then ;
3) If , then . In addition, is smooth on I.
Consequently, if (3.8) holds, then for as in (3.10),
(3.16)
We now define
This implies that
(3.17)
3.5. Monotonic Iteration
We now solve (3.14) by the following iteration: for each non-negative integer n and , we define iteratively by
(3.18)
(3.19)
Since  for every
for every 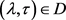 and
and , we see that
, we see that  is a well-defined family of continuous functions on D. We introduce
is a well-defined family of continuous functions on D. We introduce
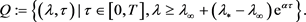
Lemma 2. For each integer 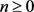 and every
and every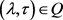 ,
, .
.
Proof. We use a mathematical induction. Assume that 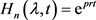 for all
for all . Then when
. Then when 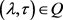 and
and , we have
, we have

Thus, 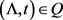 and
and  for all
for all . Consequently,
. Consequently, . Also, by (3.16),
. Also, by (3.16),
Hence, by mathematical induction, 

In the sequel, we focus on the case
Hence,

Lemma 3. For each integer

Proof. We need only consider the case


Thus,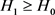

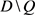
Now we establish an upper bound. We define

Lemma 4. For each integer 


Proof. We use an induction argument. Assume that the assertion holds for some

Thus, the assertion of the Lemma holds for
3.6. Solution of the Integral Equation
The family 
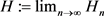

Note that when
Hence, using 


By a mathematical induction, one can derive that
Hence, we have the following:
Lemma 5. There exists a function 
In addition, H is a solution of (3.14) and has the following properties:
3.7. Lipschitz Continuity
For each
For
Lemma 6. Let 



In addition, 



Proof. When

It remains to consider the case

Thus, there exists a unique 



Here we define 






Since 




We now calculate the norm of
When
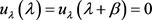



where
Hence, we have
Lemma 7. Under the condition of Lemma 6, we have
Now, applying this estimate for (3.19) and using 



Thus,
Lemma 8. For every non-negative integer n, 


Proof. Clearly, the assertion (3.25) holds when

Thus, by mathematical induction, the assertion of the Lemma holds.
Similarly, using (3.24), we can obtain an 

3.8. 
Now assume that
Differentiating 


Hence, using estimate (3.22) for
We can calculate, when 

Hence,
where
Next, we calculate for 

Note that, for
Hence,
It then follows that
Thus, we obtain
Hence, we have the following lemma.
Lemma 9. There exists a constant 

Proof. The estimate for 


Now sending
Theorem 1. Assume (3.7) and (3.8). Then the problem (3.11) admits a classical solution H that has the following properties:
1) For each 


2) For each
3.9. Uniqueness
Theorem 2. There exists a unique solution of (3.11) in the following class

Proof. Let H and 




Then

Then


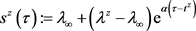

Hence, denoting 
This implies that
Now define
This implies that, for
which contradicts the boundedness of



4. Verification Theorem and Optimality of the Solution
That the optimal investment problem can be solved through the preceding results is based on a verification result which guarantees that the solution to the HJB equation is the value function corresponding to the optimal investment problem.
Theorem 3. Suppose





4.1. Preliminary Results
Lemma 10. Let 

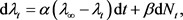

Then: 1) With


where 

2) Assume that








Proof. The assertion of the Lemma follows from a general result for the joint characteristic function of 


where 

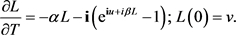
4.2. Proof of the Verification Theorem
Let 




Under the condition

Therefore, taking expectation of (4.7) we obtain
Thus,
After taking the supreme over all admissible strategies, we then obtain
Finally, one can check that if we take
This completes the verification theorem.
The above theorem provides a verification result for a general framework of stochastic volatility and double jump models.
5. Two Illustrative Cases and a Numerical Example
In the following, we present two illustrative cases. The first case of logarithm utility function is studied in [2] , where 



5.1. Logarithm Utility
When the utility function is logarithm, i.e.






Note that


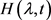
where 
By Feynman-Kac formula, 


When 
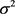


For this logarithm case, it is straightforward to show that if all jumps are negative, i.e.

5.2. The Case of Stochastic Volatility
We let 


This model is close to the one used in [10] to study effects of rare events, except that there is no diffusion term in the variance dynamics here. The dynamics of the variance becomes a type of OU process of subordinations if we extensively replace 
Given the objective problem 


The solution can be expressed as

and 

with


When the assumption (3.8) or 

We consider the special case:

where

We suppose 
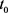
then we have
Hence 


As a conclusion, the optimal portfolio choice problem in the stochastic volatility model may meet the issue of exploding in a finite time horizon. This paper provides a sufficient condition under which a classical solution exists and exploding does not happen. Our results shall be useful in studies of a stochastic volatility model or alike.
5.3. A Numerical Example
In our proof, the monotonic iteration (3.18) and (3.19) actually suggest an iteration algorithm to find the solution numerically. Figure 2 gives a numerical example. The upper edge of curves stands for the limit of iteration corresponding to 

where 




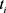

Figure 2. This figure shows the numerical iteration algorithm generates sequences converging monotonically to the limits that correspond to 
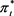
6. Conclusions and Discussions
We study the optimal portfolio choice problem in a jump-diffusion model where the jump likelihood is increased by jump itself. We establish the existence and uniqueness of a classical solution to the corresponding HJB equation. A verification theorem which guarantees the optimality of the solution is proved. Our approach relies on a monotonic iteration procedure which naturally hints a numerical algorithm. We consider CRRA utilities and a stochastic investment opportunity set which may nest interesting models in the literature.
By similar steps, our work may be extended to the case of the risk aversion (
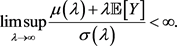
We provide a proof of existence of a continuous solution under this relaxed condition in the appendix. However, we need certain structural conditions on derivatives of 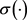

Acknowledgements
The authors acknowledge support from NSFC (No. 11371280 and No. 71771142) and NSF (DMS-1516344).
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Bian, B.J., Chen, X.F. and Zeng, X.D. (2019) Optimal Portfolio Choice in a Jump-Diffusion Model with Self-Exciting. Journal of Mathematical Finance, 9, 345-367. https://doi.org/10.4236/jmf.2019.93020
References
- 1. Merton, R. (1976) Option Pricing When Underlying Stock Returns Are Discontinous. Journal of Financial Economics, 3, 125-144.https://doi.org/10.1016/0304-405X(76)90022-2
- 2. Aït-Sahalia, Y. and Hurd, T.R. (2015) Portfolio Choice in Markets with Contagion. Journal of Financial Econometrics, 14, 1-28. https://doi.org/10.1093/jjfinec/nbv024
- 3. Barndorff-Nielsen, O.E. and Shephard, N. (2001) Non-Gaussian Ornstein-Uhlenbeck-Based Models and Some of Their Uses in Financial Mathematics. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 63, 167-241. https://doi.org/10.1111/1467-9868.00282
- 4. Benth, F.E., Karlsen, K.H. and Reikvam, K. (2003) Merton’s Portfolio Optimization Problem in Black-Scholes Market with Non-Gaussian Stochastic Volatility of Ornstein-Uhlenbeck Type. Mathematical Finance, 13, 215-244.https://doi.org/10.1111/1467-9965.00015
- 5. Delong, L. and Klüppelberg, C. (2008) Optimal Investment and Consumption in a Black-Scholes Market with Lévy-Driven Stochastic Coefficients. Annals of Applied Probability, 18, 879-908. https://doi.org/10.1214/07-AAP475
- 6. Chen, L., Peng, J., Zhang, B. and Rosyida, I. (2017) Diversified Models for Portfolio Selection Based on Uncertain Semivariance. International Journal of Systems Science, 48, 637-648. https://doi.org/10.1080/00207721.2016.1206985
- 7. Qin, Z., Kar, S. and Zheng, H. (2016) Uncertain Portfolio Adjusting Model Using Semiabsolute Deviation. Soft Computing, 20, 717-725.https://doi.org/10.1007/s00500-014-1535-y
- 8. Hawkes, A.G. (1971) Spectra of Some Self-Exciting and Mutually Exciting Point Processes. Biometrika, 58, 83-90. https://doi.org/10.1093/biomet/58.1.83
- 9. Aït-Sahalia, Y., Cacho-Diaz, J. and Laeven, R.J.A. (2015) Modeling Financial Contagion Using Mutually Exciting Jump Processes. Journal of Financial Economics, 117, 585-606. https://doi.org/10.1016/j.jfineco.2015.03.002
- 10. Liu, J., Longstaff, F. and Pan, J. (2003) Dynamic Asset Allocation with Event Risk. Journal of Finance, 58, 231-259. https://doi.org/10.1111/1540-6261.00523
Appendix. Existence of a Continuous Solution under a Relaxed Condition
In this appendix, we establish the existence of a solution H of (3.11) under the condition (3.9) instead of the condition (3.8). For each
We write the partial differential equation in (3.11) as
where
We define a family 



In term of characteristic curves, the linear problem for 
1) Note that
It then follows by a comparison principle for the equation for 

2) Next, assume that 

Here we use the fact that 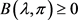



3) Note that, since 
Thus,
Note that if 


we have
Now assume that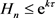
It then follows by comparison principle that
Thus we have, for each integer
Then