Journal of Mathematical Finance
Vol.05 No.02(2015), Article ID:56278,5 pages
10.4236/jmf.2015.52016
The Stochastic Error Rate Estimation of Prediction Distributions
Hafedh Faires
Department of Mathematics and Statistics, Al Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia
Email: hafedh.faires@hotmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 March 2015; accepted 11 May 2015; published 13 May 2015
ABSTRACT
The estimation of claims reserves is usually done by applying techniques called IBNR techniques within a stochastic framework. The main objective of this paper is to predict the partial reserve and to estimate the error rate of prediction distributions by using the stochastic model proposed in [1] .
Keywords:
Reserving Claims, EDS, Error Rate, Prediction Distributions

1. Introduction
The calculation of the provisions for disaster payments is intended to allow the integral payment of the commitments to the policy-holders and the recipients of the contract. The provisions measure the commitments that the insurer still has to honor. Nevertheless, this countable concept requires a subjacent probabilistic model since it allows one to define the ultimate claim, taking into account the disasters not yet declared, but which have occurred, the disasters not sufficiently funded. Reserves are given by evaluating the provisions for each contract, IBNR (sinister not yet declared) and IBNER (sinister not sufficiently funded). Traditional methods of provisioning (by triangulation) rest on the assumption that the data are homogeneous and in sufficient quantity to ensure a certain stability and a certain credibility. The purpose of this paper is to propose a stochastic extension of the Chain-Ladder model concerning the partial prediction reserve and to estimate the error rate of prediction distributions, which seems to be closer to reality for us than the existing methods of Schnieper [2] ; Mack [3] ; Liu and Verrall [4] ; Verrall and England [5] .
Models in which parameters move between a fixed number of regimes with switching controlled by an unobserved stochastic process, are very popular in a great variety of domains (Finance, Biology, Meteorology, Networks, etc.). This is notably due to the fact that this additional flexibility allows the model to account for random regime changes in the environment. In this paper we consider the prediction of partial reserve and consider the estimation of error rate of prediction distributions for a model described by a stochastic differential equation (SDE) with Markov regime-switching (MRS), i.e., with parameters controlled by a finite state continuous-time Markov chain (CTMC) [1] and [6] . Such a model was used, for example, in Deshpande and Ghosh (2008) [7] , to price options in a regime switching market. In such a setting, the parameter estimation problem posed a real challenge, mainly due to the fact that the paths of the CTMC were unobserved. A standard approach consists in using the celebrated EM algorithm (Dempster, Laird and Rubin, 1977) [8] as proposed, for example in Elliott, Malcolm and Tsoi (2003) [9] and Hamilton (1990) [10] , study this problem using a filtering approach.
The rest of the paper is structured as follows. In Section 2, we present the stochastic model for our problem. Section 3 is devoted to predicting the claims reserves variance. We conclude with a summary in the last section.
2. Hypotheses and Description of the Model
We suppose that the available data have a triangular form indexed by the year of accident, i, and the development time, t. Given a triangle, on T years, the goal is to consider models using a minimum of parameters, in order to envisage the best possible amounts of payments of future disasters. We note the evolution of the amounts of payments of the cumulated real disasters obtained by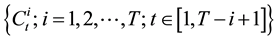 .
.
 indicates the evolution of the cumulated real disasters indexed by the year of accident, i, and the time of development, t. We suppose that the increase in the disasters obtained
indicates the evolution of the cumulated real disasters indexed by the year of accident, i, and the time of development, t. We suppose that the increase in the disasters obtained 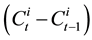 is the sum of the disasters not sufficiently funded
is the sum of the disasters not sufficiently funded  and of the disasters not declared yet claims
and of the disasters not declared yet claims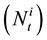 . In the paper [1] the following relations between C, N and D is proposed.
. In the paper [1] the following relations between C, N and D is proposed.
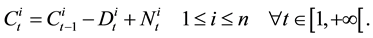 (1)
(1)
We indicate 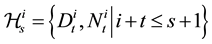 for all the variables in the triangles D and N observed until the moment s.
for all the variables in the triangles D and N observed until the moment s.
To simulate the future claims, it is supposed that the not sufficiently funded claims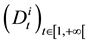 , the stochastic differential equation of diffusion and the not yet incurred claims
, the stochastic differential equation of diffusion and the not yet incurred claims 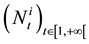 are governed by the stochastic dif-
are governed by the stochastic dif-
ferential equation of Black and Scholes with jump. This assumption on the probability density function of 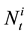 ensures positivity and for
ensures positivity and for 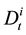 ensures the membership
ensures the membership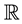 , contrary to what is proposed by Liu and Verrall [4] .
, contrary to what is proposed by Liu and Verrall [4] .
Conditionally with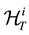 , we simulate the distribution of
, we simulate the distribution of 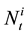 as solution of the following stochastic differential equation:
as solution of the following stochastic differential equation:
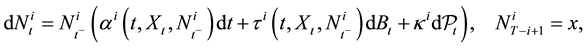 (2)
(2)
where 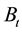 is a standard Brownian motion on
is a standard Brownian motion on





and 
Conditionally with


where 










For any state 





where 


Let us define the log-returns 

Given a path 




Then, conditional on the path X, the solutions of the Equations (2) and (3) are respectively given by :
・ the solution of the first Equation (2) is

and,
・ 


3. Predicted Claims Reserves Variance
The main reason for using stochastic models is to estimate the error rate of prediction distributions. It is useful for solvency, capital modelling and measurement of risk. We begin by proving how the predicted error rate can be calculated. The predicted error rate is obtained from the predicted variance of the partial reserve of loss. We
remember that 




the partial reserve by:


The mean square error prediction of 
Theorem 3.1 Let 


Proof. The mean square error prediction of the partial reserve can be written as follows

Using the fact that
and
As a first step, we calculate
We calculate the second term (12), taking into account
and
Then
4. Conclusion
We have studied the Bayesian approach for the regime switching geometric Brownian motion proposed by [1] . It has been observed empirically that sinisters fluctuate among periods of high, moderate and low volatilities, so in this paper the estimation of the error rate of prediction distributions is proposed. For the future research, our developments raise an interesting axe when the Markov chain is hidden.
Acknowledgements
We would like to thank the reviews for the comments.
References
- Faires, H. (2014) Non-Life Claims Reserves Using Dirichlet Random Environment. International Journal of Engineering Research and Applications (IJERA), 4, 63-77.
- Schnieper, R. (1991) Separating True IBNR and IBNER Claims. ASTIN Bulletin, 21, 111-127.
- Mack, T. (2000) Distribution-Free Calculation of the Standard Error of Chain Ladder Reserve Estimates. ASTIN Bulletin, 23, 214-225.
- Liu, H.J. and Verrall, R. (2002) Predictive Distributions for Reserves which Separate True IBNR and IBNER Claims. http://www.actuaries.org/ASTIN/Colloquia/Orlando/Papers/Liu.pdf
- Verrall, R.J. and England, P.D. (2000) Comments on: “A Comparison of Stochastic Models That Reproduce Chain Ladder Reserve Estimates”, by Mack and Venter. Insurance: Mathematics and Economics, 26, 109-111. http://ideas.repec.org/a/eee/insuma/v26y2000i1p109-111.html
- Faires, H. (2012) SDEs in Dirichlet Random Environment. International Journal of Statistics and Systems, 1, 55-66.
- Deshpande, A. and Ghosh, M.K. (2007) Risk Minimizing Option Pricing in a Regime Switching Market. Stochastic Analysis and Applications, 28, 313-324.
- Dempster, A.P., Laird, R.M. and Rubin, D.B. (1977) Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society. Series B (Methodological), 39, 1-38.
- Elliott, R.J., Malcolm, W.P. and Tsoi, A.H. (2003) Robust Parameter Estimation for Asset Price Models with Markov Modulated Volatilities. Journal of Economics Dynamics and Control, 27, 1391-1409. http://dx.doi.org/10.1016/S0165-1889(02)00064-7
- Hamilton, J. A. (1990) Analysis of Time Series Subject to Changes in Regime. Journal of Econometrics, 45, 39-70. http://dx.doi.org/10.1016/0304-4076(90)90093-9













