Open Journal of Statistics
Vol.06 No.06(2016), Article ID:72617,9 pages
10.4236/ojs.2016.66087
On the Restricted Almost Unbiased Ridge Estimator in Logistic Regression
Nagarajah Varathan1,2, Pushpakanthie Wijekoon3
1Postgraduate Institute of Science, University of Peradeniya, Peradeniya, Sri Lanka
2Department of Mathematics and Statistics, University of Jaffna, Jaffna, Sri Lanka
3Department of Statistics and Computer Science, University of Peradeniya, Peradeniya, Sri Lanka

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 20, 2016; Accepted: December 3, 2016; Published: December 8, 2016
ABSTRACT
In this article, the restricted almost unbiased ridge logistic estimator (RAURLE) is proposed to estimate the parameter in a logistic regression model with exact linear restrictions when there exists multicollinearity among explanatory variables. The performance of the proposed estimator over the maximum likelihood estimator (MLE), ridge logistic estimator (RLE), almost unbiased ridge logistic estimator (AURLE), and restricted maximum likelihood estimator (RMLE) with respect to different ridge parameters is investigated through a simulation study in terms of scalar mean square error.
Keywords:
Multicollinearity, Ridge Estimator, Almost Unbiased Ridge Logistic Estimator, Linear Restrictions, Scalar Mean Square Error

1. Introduction
Multicollinearity inflates the variance of the maximum likelihood estimator (MLE) in the logistic regression. As a result, one may not obtain an efficient estimate for the parameter 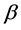 in the logistic regression model. To combat the multicollinearity in logistic regression, several alternative techniques have been proposed in the literature. One of the most famous techniques is to consider suitable biased estimators in place of Maximum likelihood estimator. The biased estimators proposed in the literature, are the Ridge Logistic Estimator (RLE) (Schaefer et al., 1984 [1] ), Liu Logistic Estimator (LLE) (Liu, 1993 [2] , Urgan and Tez, 2008 [3] , and Mansson et al., 2012 [4] ), Principal Component Logistic Estimator (PCLE) (Aguilera et al., 2006 [5] ), Modified Logistic Ridge Estimator (MLRE) (Nja et al., 2013 [6] ), Liu-type estimator (Inan and Erdogan, 2013 [7] ), and Almost Unbiased Liu Logistic Estimator (AULLE) (Xinfeng, 2015 [8] ). Morever, Asar (2015) [9] , proposed some new methods to solve the multicollinearity in logistic regression by introducing new methods of estimating the shrinkage parameter in Liu-type estimators. Only the sample information was used in all the above estimation procedures. An alternative technique suggested to solve the multicollinearity problem is to consider parameter estimation with some linear restrictions on the unknown parameters, which are generally based on prior information of the sample data, and further they may be in the exact or stochastic form. By incorporating linear restrictions to the sample information, different types of biased estimators were introduced in the literature, and some researchers have incorporated these estimators with the logistic regression estimator to improve its performance. In the presence of exact linear restrictions in addition to sample logistic regression model, Duffy and Santer (1989) [10] introduced the restricted maximum likelihood estimator (RMLE) by incorporating the restricted least squares estimator based on exact linear restriction to the logistic regression. Later, the Restricted Logistic Ridge Estimator (Asar et al., 2016 [11] ), Restricted Logistic Liu Estimator (RLLE) (Şiray et al., 2015 [12] ), Modified Restricted Liu Estimator (Wu, 2016 [13] ), Restricted two parameter Liu type estimator (Asar et al., 2016 [14] ) were introduced to the logistic regression with exact linear restrictions. In the presence of stochastic linear restrictions in addition to sample logistic regression model, Nagarajah and Wijekoon (2015) introduced the Stochastic Restricted Maximum Likelihood Estimator (SRMLE). Following Nagarajah and Wijekoon (2015) [15] , the Stochastic Restricted Ridge Maximum Likelihood Estimator (SRRMLE) was proposed by Varathan and Wijekoon (2016) [16] by incorporating Ridge Logistic Estimator (RLE) with the SRMLE.
in the logistic regression model. To combat the multicollinearity in logistic regression, several alternative techniques have been proposed in the literature. One of the most famous techniques is to consider suitable biased estimators in place of Maximum likelihood estimator. The biased estimators proposed in the literature, are the Ridge Logistic Estimator (RLE) (Schaefer et al., 1984 [1] ), Liu Logistic Estimator (LLE) (Liu, 1993 [2] , Urgan and Tez, 2008 [3] , and Mansson et al., 2012 [4] ), Principal Component Logistic Estimator (PCLE) (Aguilera et al., 2006 [5] ), Modified Logistic Ridge Estimator (MLRE) (Nja et al., 2013 [6] ), Liu-type estimator (Inan and Erdogan, 2013 [7] ), and Almost Unbiased Liu Logistic Estimator (AULLE) (Xinfeng, 2015 [8] ). Morever, Asar (2015) [9] , proposed some new methods to solve the multicollinearity in logistic regression by introducing new methods of estimating the shrinkage parameter in Liu-type estimators. Only the sample information was used in all the above estimation procedures. An alternative technique suggested to solve the multicollinearity problem is to consider parameter estimation with some linear restrictions on the unknown parameters, which are generally based on prior information of the sample data, and further they may be in the exact or stochastic form. By incorporating linear restrictions to the sample information, different types of biased estimators were introduced in the literature, and some researchers have incorporated these estimators with the logistic regression estimator to improve its performance. In the presence of exact linear restrictions in addition to sample logistic regression model, Duffy and Santer (1989) [10] introduced the restricted maximum likelihood estimator (RMLE) by incorporating the restricted least squares estimator based on exact linear restriction to the logistic regression. Later, the Restricted Logistic Ridge Estimator (Asar et al., 2016 [11] ), Restricted Logistic Liu Estimator (RLLE) (Şiray et al., 2015 [12] ), Modified Restricted Liu Estimator (Wu, 2016 [13] ), Restricted two parameter Liu type estimator (Asar et al., 2016 [14] ) were introduced to the logistic regression with exact linear restrictions. In the presence of stochastic linear restrictions in addition to sample logistic regression model, Nagarajah and Wijekoon (2015) introduced the Stochastic Restricted Maximum Likelihood Estimator (SRMLE). Following Nagarajah and Wijekoon (2015) [15] , the Stochastic Restricted Ridge Maximum Likelihood Estimator (SRRMLE) was proposed by Varathan and Wijekoon (2016) [16] by incorporating Ridge Logistic Estimator (RLE) with the SRMLE.
Wu and Asar (2016) [17] has proposed a new biased estimator called Almost Unbiased Ridge Logistic Estimator (AURLE), and shown its performance over the other available estimators. In this article, we further improve the logistic regression estimator by combining AURLE with RMLE, and name it as the Restricted Almost Unbiased Ridge Logistic Estimator (RAURLE). Further, the performance of RAURLE based on estimated ridge parameters using different methods given in the literature was considered, and compared each of these cases with MLE, RLE, AURLE and RMLE. The proceeding sections of the article are organized as follows. The model specification and estimation are discussed in Section 2. The proposed estimator and its asymptotic properties are given in Section 3. Section 4 describes the existing methods related to some ridge parameters. In Section 5, the performance of the proposed estimator by considering different ridge parameters is compared with respect to the scalar mean squared error (SMSE) with MLE, RLE, AURLE and RMLE by performing a Monte Carlo simulation study. Finally, conclusions of the study are presented in Section 6.
2. Model Specification and Estimation
Consider the following logistic regression model
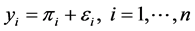 (1)
(1)
which follows Bernoulli distribution with parameter 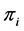 as
as
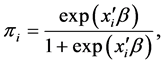 (2)
(2)
where 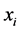 is the ith row of X, which is an
is the ith row of X, which is an  data matrix with p predictor variables and
data matrix with p predictor variables and 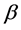 is a
is a 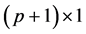 vector of coefficients,
vector of coefficients, 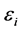 are independent with mean zero and variance
are independent with mean zero and variance 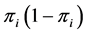 of the response
of the response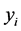 . The maximum likelihood estimator (MLE) of
. The maximum likelihood estimator (MLE) of 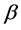 can be obtained as follows:
can be obtained as follows:
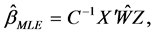 (3)
(3)
where ; Z is the column vector with ith element equals
; Z is the column vector with ith element equals
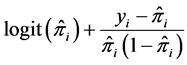 and
and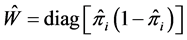 , which is an unbiased estimate of
, which is an unbiased estimate of
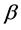 . The covariance matrix of
. The covariance matrix of 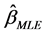 is
is
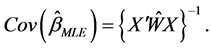
In the presence of multicollinearity, Schaefer et al. (1984) [1] proposed to incorporate the Logistic Ridge Estimator (LRE), in place of the MLE in the logistic regression model (1)
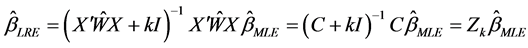
where 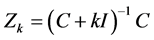
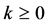
The asymptotic properties of LRE:
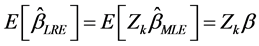
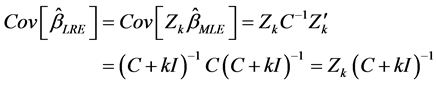
However the LRE is a biased estimator which produces inconsistent estimates for the parameter (Wu and Asar, 2016 [17] ). Consequently, the Almost Unbiased Ridge Logistic Estimator (AURLE) was introduced by Wu and Asar (2016) [17] and it is defined as
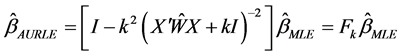
where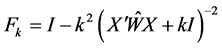
And the asymptotic properties of AURLE:
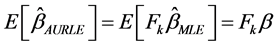
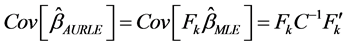
As another remedial action for multicollinearity, one may use the exact linear restrictions in addition to the sample logistic regression model (1). The resulting esti- mator is called as Restricted estimator.
Suppose that the following exact restriction is given in addition to the general logistic regression model (1).
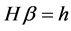
where H is a 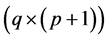
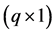
In the presence of the above restriction (11) in addition to the logistic regression model (1), Duffy and Santner (1989) [10] proposed the following Restricted Maximum Likelihood Estimator (RMLE).
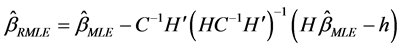
The asymptotic mean and variance of 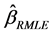
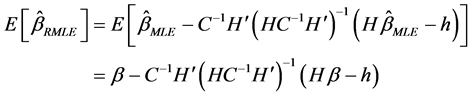
and
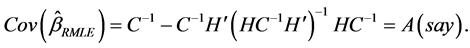
Consequently the bias of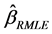
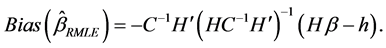
3. The Proposed Estimator
To improve the performance of the estimators further, in this section, by combining AURLE and RMLE, we propose a new estimator which is called as the Restricted Almost Unbiased Ridge Logistic Estimator (RAURLE) and defined as
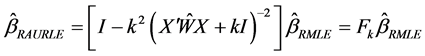
where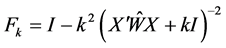
The asymptotic properties of 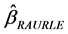
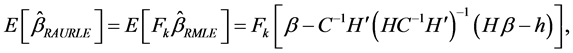
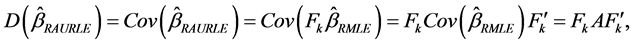
and
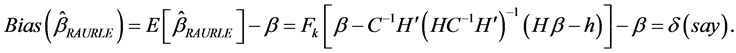
Consequently, the mean square error can be obtained as,
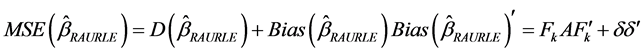
4. Some Ridge Estimators
Now we consider the existing methods to obtain an estimated value for the ridge parameter k, since RAURLE depends on k. Many researchers suggested various methods of estimating the ridge parameter in the ridge regression approach and recently this estimation method is added to the logistic regression. In this research, we have considered the following existing ridge parameter estimation methods to compare the performance of the proposed estimator with some existing estimators in logistic regression.
1) Hoerl and Kennard (1970) [18] ;
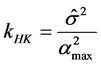
where 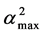
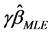
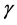
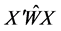
2) Hoerl et al. (1975) [19] ;
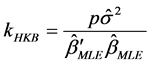
where p is the number of predictor variables in the model (1).
3) Lawless and Wang (1976) [20] ;
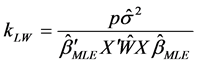
4) Lindley and Smith (1972) [21] ;
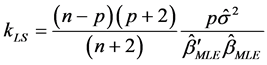
5) Schaefer et al. (1984) [1] ;
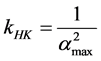
5. Simulation Study
It is difficult to compare the mean square error of the estimators theoretically, since none of the estimators MLE, RLE, AURLE, RMLE and RAURLE are not always superior. So, we use Monte Carlo simulation to examine the performance of the proposed estimator over the existing estimators under different levels of multicolli- nearity. Following McDonald and Galarneau (1975) [22] and Kibria (2003) [23] , the explanatory variables are generated using the following equation.
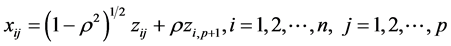
where 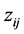
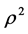
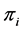
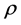
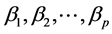
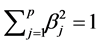

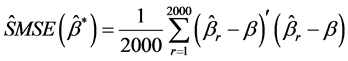
where 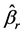
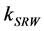
6. Concluding Remarks
In this paper, we proposed a restricted almost unbiased ridge logistic estimator (RAURLE) in logistic regression with exact linear restrictions when the explanatory variables are highly correlated. Through a Monte Carlo simulation study, we examined
Table 1. The estimated SMSE values for different k, when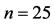
Table 2. The estimated SMSE values for different k, when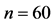
Table 3. The estimated SMSE values for different k, when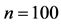
the performance of the proposed estimator over some existing estimators MLE, RLE, AURLE and RMLE in terms of scalar mean square error. Also, five different choices of existing ridge parameter estimates were used to compare the estimators. The results show that the newly proposed estimator outperforms all the other estimators considered in this study under the selected values of n, r, and k by means of SMSE.
Acknowledgements
We thank the Editor and the referee for their comments and suggestions, and the Postgraduate Institute of Science, University of Peradeniya, Sri Lanka for providing necessary facilities to complete this research.
Cite this paper
Varathan, N. and Wijekoon, P. (2016) On the Restricted Almost Unbiased Ridge Estimator in Logistic Regression. Open Journal of Statistics, 6, 1076-1084. http://dx.doi.org/10.4236/ojs.2016.66087
References
- 1. Schaefer, R.L., Roi, L.D. and Wolfe, R.A. (1984) A Ridge Logistic Estimator. Communications in Statistics - Theory and Methods, 13, 99-113.
https://doi.org/10.1080/03610928408828664 - 2. Liu, K. (1993) A New Class of Biased Estimate in Linear Regression. Communications in Statistics -Theory and Methods, 22, 393-402.
https://doi.org/10.1080/03610929308831027 - 3. Urgan, N.N. and Tez, M. (2008) Liu Estimator in Logistic Regression When the Data Are Collinear. International Conference. “Continuous Optimization and Knowledge-Based Technologies”, 323-327.
- 4. Mansson, G., Kibria, B.M.G. and Shukur, G. (2012) On Liu Estimators for the Logit Regression Model. The Royal Institute of Techonology, Centre of Excellence for Science and Innovation Studies (CESIS), Sweden, Paper No. 259.
- 5. Aguilera, A.M., Escabias, M. and Valderrama, M.J. (2006) Using Principal Components for Estimating Logistic Regression with High-Dimensional Multicollinear Data. Computational Statistics & Data Analysis, 50, 1905-1924.
https://doi.org/10.1016/j.csda.2005.03.011 - 6. Nja, M.E., Ogoke, U.P. and Nduka, E.C. (2013) The Logistic Regression Model with a Modified Weight Function. Journal of Statistical and Econometric Method, 2, 161-171.
- 7. Inan, D. and Erdogan, B.E. (2013) Liu-Type Logistic Estimator. Communications in Statistics - Simulation and Computation, 42, 1578-1586.
https://doi.org/10.1080/03610918.2012.667480 - 8. Xinfeng, C. (2015) On the Almost Unbiased Ridge and Liu Estimator in the Logistic Regression Model. International Conference on Social Science, Education Management and Sports Education, Atlantis Press, Amsterdam, 1663-1665.
- 9. Asar, Y. (2015) Some New Methods to Solve Multicollinearity in Logistic Regression. Communications in Statistics - Simulation and Computation, Online.
https://doi.org/10.1080/03610918.2015.1053925 - 10. Duffy, D.E. and Santner, T.J. (1989) On the Small Sample Prosperities of Norm-Restricted Maximum Likelihood Estimators for Logistic Regression Models. Communications in Statistics -Theory and Methods, 18, 959-980.
https://doi.org/10.1080/03610928908829944 - 11. Asar, Y., Arashi, M. and Wu, J. (2016) Restricted Ridge Estimator in the Logistic Regression Model. Communications in Statistics - Simulation and Computation, Online.
https://doi.org/10.1080/03610918.2016.1206932 - 12. Siray, G.U., Toker, S. and Kaciranlar, S. (2015) On the Restricted Liu Estimator in Logistic Regression Model. Communications in Statistics - Simulation and Computation, 44, 217-232.
https://doi.org/10.1080/03610918.2013.771742 - 13. Wu, J. (2016) Modified Restricted Liu Estimator in Logistic Regression Model. Computational Statistics, 31, 1557.
https://doi.org/10.1007/s00180-015-0609-3 - 14. Asar, Y., Erisoglu, M. and Arashi, M. (2016) Developing a Restricted Two Parameter Liu-Type Estimator: A Comparison of Restricted Estimators in the Binary Logistic Regression Model. Communications in Statistics - Theory and Methods, Online.
https://doi.org/10.1080/03610926.2015.1137597 - 15. Nagarajah, V. and Wijekoon, P. (2015) Stochastic Restricted Maximum Likelihood Estimator in Logistic Regression Model. Open Journal of Statistics, 5, 837-851.
https://doi.org/10.4236/ojs.2015.57082 - 16. Varathan, N. and Wijekoon, P. (2016) Ridge Estimator in Logistic Regression under Stochastic Linear Restriction. British Journal of Mathematics & Computer Science, 15, 1.
https://doi.org/10.9734/BJMCS/2016/24585 - 17. Wu, J. and Asar, Y. (2016) On Almost Unbiased Ridge Logistic Estimator for the Logistic Regression Model. Hacettepe Journal of Mathematics and Statistics, 45, 989-998.
- 18. Hoerl, E. and Kennard, R.W. (1970) Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics, 12, 55-67.
https://doi.org/10.1080/00401706.1970.10488634 - 19. Hoerl, E., Kennard, R.W. and Baldwin, K.F. (1975) Ridge Regression: Some Simulations. Communications in Statistics, 4, 105-123.
https://doi.org/10.1080/03610927508827232 - 20. Lawless, J.F. and Wang, P. (1976) A Simulation Study of Ridge and Other Regression Estimators. Communications in Statistics - Theory and Methods, 14, 307-323.
https://doi.org/10.1080/03610927608827353 - 21. Lindley, D.V. and Smith, A.F.M. (1972) Bayes Estimate for the Linear Model (with Discussion) Part 1. Journal of the Royal Statistical Society, Ser B, 34, 1-41.
- 22. McDonald, G.C. and Galarneau, D.I. (1975) A Monte Carlo Evaluation of Some Ridge-Type Estimators. Journal of the American Statistical Association, 70, 407-416.
https://doi.org/10.1080/01621459.1975.10479882 - 23. Kibria, B.M.G. (2003) Performance of Some New Ridge Regression Estimators. Communications in Statistics - Theory and Methods, 32, 419-435.
https://doi.org/10.1081/sac-120017499


