Open Journal of Statistics
Vol.05 No.07(2015), Article ID:62039,12 pages
10.4236/ojs.2015.57073
The Burr XII Distribution Family and the Maximum Entropy Principle: Power-Law Phenomena Are Not Necessarily “Nonextensive”
F. Brouers
Institute of Physics, University of Liège, Liège, Belgium

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 27 September 2015; accepted 15 December 2015; accepted 18 December 2015

ABSTRACT
In this paper, we recall for physicists how it is possible using the principle of maximization of the Boltzmann-Shannon entropy to derive the Burr-Singh-Maddala (BurrXII) double power law probability distribution function and its approximations (Pareto, loglogistic.) and extension (GB2…) first used in econometrics. This is possible using a deformation of the power function, as this has been done in complex systems for the exponential function. We give to that distribution a deep stochastic interpretation using the theory of Weron et al. Applied to thermodynamics, the entropy nonextensivity can be accounted for by assuming that the asymptotic exponents are scale dependent. Therefore functions which describe phenomena presenting power-law asymptotic behaviour can be obtained without introducing exotic forms of the entropy.
Keywords:
Buur XII Distribution, Singh-Maddala Distribution, Lévy Function, Entropy, Non-Equilibrium Thermodynamics, Complex Systems, Nonextensivity

1. Introduction
In this paper, we want to show how the BurrrXII-Singh-Maddala (BSM) [1] [2] distribution function, known also as the q-Weibull distribution can be naturally derived from the maximum entropy principle using the Boltzmann-Shannon entropy with well-defined constraints including a generalization of the definition of the moment [3] -[5] similar to the deformation of the exponential. This is what has been done in Section 5. In Section 2 and 3, we recall the properties of the BSM distribution and its applications in physics and chemistry. Section 4 is devoted to summarize the Weron stochastic interpretation of the BSM probability distribution which has allowed us in Section 7 and 8 to give a novel interpretation of the concept of nonextensivity.
This paper has been written for several reasons.
The BSM distribution has been used in a variety apparently independent fields: econometrics [6] [7] , actuary sciences [8] [9] , hydrology [5] , forestry [10] , sorption theories [11] [12] , fractal kinetics [13] -[20] , pharmacokinetics [21] , relaxation and reaction phenomena [22] [23] . Two of its approximations, the Weibull and the Hill equations are widely used in materials sciences [24] - [26] , medical sciences in particular cancer remission and pharmacokinetic [27] - [29] , physico-chemistry in particular complex and enzymatic reactions [30] - [32] , meteorology [33] adsorption [34] [35] , economy [36] etc. We have quoted here some of the most recent papers using the BSM, the Weibull and Hill distributions. The BSM distribution and some of the distribution derived from it give rise asymptotically to power-laws at high or (and) small values of the variable. For some values of the parameters, they belong to the family of Lévy heavy tail functions [37] .
There is a widespread belief in physics that the phenomena characterized by power laws behaviour, ubiquitous in nature, should require extensions of the Boltzmann-Shannon (BS) entropy and that the BS entropy should be restricted to the family of Gaussian and exponential laws i.e. the distributions which obey the classical central limit theorem. Among the more than 20 proposed generalized entropies, the most famous are the Reyni [38] and the Tsallis [39] [40] entropies. To avoid divergences of the moments, Reyni introduces in the expression of the entropy powers of the probability function. Tsallis has used the same procedure introducing so-called “escort probabilities”. He proposes a form of entropy which has the property to be nonextensive ab-initio and derives the so-called Tsallis distribution to extend the exponential distributions in thermodynamics.
We show in details, as this has been noticed by previous authors before us, that this is not necessarily true. It is possible quite naturally to obtain power law distributions by generalizing the definition of moments or using constraints determined by the data observation and keeping the BS entropy as a starting point for the maximization procedure [4] [5] [41] - [47] . M. Visser [48] claims that power laws can be obtained by applying maximum entropy ideas directly to the Shannon entropy subject only to one constraint that the logarithm of the observable quantity is specified.
The BSM cumulative distribution functions are characterized by three parameters, two form factors a and c and one scale parameter b. The power law exponents corresponding to, respectively the asymptotic behaviour of small and large values of its argument are a and μ = a/c. The Tsallis distribution, derived from the maximization of Tsallis entropy is the survival part of the cumulative BSM distribution when a is equal to one. This density function has been used in the literature to fit many experimental data. These data can be fitted with the same degree of precision using both density distributions. This has created confusion on the value of the so-called entropic index q which is different in both cases.
It must be stressed that the BSM density function includes an exponent a which is absent from the Tsallis density function. The experimental observations, which dates back to the beginning of the last century [49] -[51] show that in natural phenomena, the exponent a is rarely equal to one and that the relation of μ with the two parameters a and c is an important feature which is ignored in Tsallis formalism. The far future is not independent on the early beginning. We know it from cosmology and from all organism evolutions.
However, we will show in Section 8 that nonextensivity of the entropy may arise from the scale dependence of the characteristic exponents.
As a consequence of the previous points we will show that phenomena described by function with one or two tails asymptotic power laws have not necessarily to be obtained by the maximization of an extension of the BS entropy. This is has been known for a long time in fields outside of physics such as hydrology and econometrics.
2. The Burr-Singh-Madalla Distribution
The BSM cumulative density function is written as:
 (1)
(1)
where a and c are form factors and b is a scaling factor.
Its density function is easily obtained by differentiation
 (2)
(2)
It is solution of a differential equation
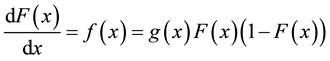 (3)
(3)
The function
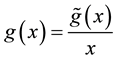 where
where
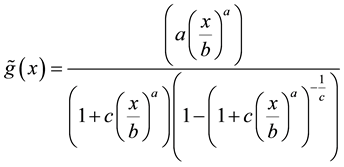 (4)
(4)
The function
 varies slowly from a to
varies slowly from a to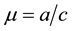 . One has:
. One has:
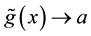 when
when
 and
and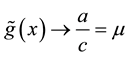 , when
, when .
.
The differential equation describes a birth and death process modulated by a quasi hyperbolic function which can be modified to accommodate more complex situations.
The cumulative distribution function
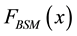 exhibits asymptotically two power laws: one for
exhibits asymptotically two power laws: one for
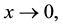
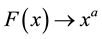 and one for
and one for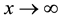 ,
,



The survival part of the cumulative function is given by

which has the same form as the Tsallis density function if


index. By contrast the power of the BSM density function is

the so called “escort probability” in Tsallis formalism. The Lévy power law exponent


and this has to be considered in interpreting experimental results.
As the mathematician Vladimir Arnold once said “Differential equations are the source of the development of modern sciences”, one can consider Equation (3) as the natural starting point to study complex systems in the same way the exponential is solution of a differential equation and is the natural starting point for the description of simple systems. For instance, it has been used in epidemiology [52] , the influence of the sanitary authorities to its propagation being accounted for by modifying the function g(x) accordingly. It must be reminded that the approximation g(x) = 1 is the famous Verhulst [53] equation whose discrete version is one of the paradigms in the theory of chaos [54] .
3. Application of the BSM Distribution Function in Physics
The BSM function has been used to establish a three parameters fractal kinetic equation which has been employed with some success to characterize macroscopically the sorption (ad-, chemi-, bio-) in gaseous and aqueous phase [11] [12] as well as in the theory of relaxation [22] [23] to justify the two asymptotic behaviours of the Havriliak-Negami formula [55] in the frequency range. It has been used also to show that some of the empirical isotherms (Langmuir [56] , Sips-Hill [57] and Brouers-Sotolongo [34] isotherms) are well defined approximations of the BSM function and therefore enjoy the properties of statistical distributions.
The work of K. Weron and its collaborators has given a deep physical understanding of this distribution. Indeed they have derived the BSM survival function in the theory of relaxation by means of stochastic arguments linking the observed macroscopic properties to the mesooscopic and microscopic energetic and geometric organisation (fractal scaling, clustering, self-organiszation) of complex heterogeneous systems. We will deal with this interpretation in the next paragraph.
4. Stochastic Interpretation of the BSM Distribution
The analytical form of the BSM distribution function can be justified and the parameters


The quantities




where

Two situations have to be considered: the expecting value of






where


It is the Weibull survival function quite frequent in physical, chemical and biological phenomena. The parameter a arises from the stable scaling properties at the micro and mesoscopic levels. When
The BSM distribution function can be obtained by considering a more complex situation where due to complex frustrations, the number of reacting element is not fixed and is itself a random variable. In that case Equation (8) should be replaced by

As argued by Weron et al. the fluctuations of



Then the survival probability function of the entire system is

The solution of which has been obtained by Rodriguez [60] more than forty years ago

This is the BSM survival distribution function in the time domain. The corresponding density function is

In this derivation of the BSM function, the parameter c appears to be a measure of aggregation with one or several characteristic lengths.
5. The BSM Density Function Derived from the Maximization of the BS Entropy
Starting from the Boltzmann-Shannon entropy

We determine



And generalizing the definition of the power of a variable in the same spirit as the definition of the deformed exponential

The third constraint can then be expressed as:

The constraint conditions can be understood as known prior information which can be used to achieve a least biased distribution.
Using the method of Lagrange optimization method and defining

The maximization of S(x) is obtained by solving the equation:



With the normalization constant determined by the partition function

The values of the



one gets finally, given the constraints



We have therefore

with

This finally gives the BSM density function (Equation (2)).
The expression for the k-th moment is given by [61]

The Tsallis density function (a = 1) is the survival function of

with the constraints

These results have already been obtained with other notations in the field of econometrics and meteorology [3] -[5] [45] . The same procedure has been used also for 4-parameters generalization of the BSM (GB2 foe example) in the econometrics literature. One recovers our results when the extra parameter is put to one or zero according to the type of extension.
Another tail distribution, the Cauchy distribution

The Weibull and the Pareto and Cauchy tail distribution entropies are well known and have been derived in the classical books on entropy maximization method [62] .
For c = 0, one recovers the well-known results for the Weibull distribution


with

For c = 1, the log-logistic-Hill-Fisk constraints

with

Finally it must be noted that if

6. Expressions of the Entropy
Making use of the results of the previous section, one can now write the expressions of the entropy corresponding to the various approximations.
From the general definition

We get for the BSM distribution

for the Weibull distribution

For the log-logistic-Hill-Fisk distribution

and



The general form of the entropy is therefore

K(a, c) is a constant that we can consider as the origin of the entropy for a couple of values a and c. The previous results are therefore compatible with the extensivity of the BS entropy. If we have two subsystems 1 and 2 added to form a larger system with have:

This is only true if
7. Implications in Thermodynamics
The aim of this paper is to discuss the probabilistic and stochastic foundation of the use of the BSM distribution to describe physical and chemical complex systems characterized by power-law, Levy and extreme value distributions. We will nevertheless in the last section touch the problem of the application of this formalism to thermodynamics.
In the case (a = 1, c = 0, q = 1), we have

The corresponding canonical entropy is

In the case a = 1, which is the case used in extensions of the classical thermodynamics, one has






Therefore if

The usual canonical thermodynamics expression for the entropy (Equation (47)) can be recovered if one introduces a c-temperature assuming that



which gives a c-depending temperature depending on the evolution of



8. Nonextensivity
Nonextensivity observed in systems with long range interactions can be accounted for if the parameter c (and q) are scale dependent. One can use an argument used by C. Beck [63] to obtain a quasi nonexpensive entropy from a superstatistic version of the Tsallis entropy. I quote “in other words q(r) is a strictly monotonously decreasing function of the scale, just as observed in experiments”. This means that, in the BSM formalism, if the parameter c decreases with an increase of the volume; the additive property of the entropy is no longer respected since

Moreover, the system is no longer in an equilibrium state since


This interpretation of nonextensivity is in agreement with the signification of the parameter c which is related to the cluster organization (possibly multifractal) of the heterogeneous system as discussed in Section 4.
9. Conclusion
In conclusion, we think that physicists have to learn a lot from the progress made the last decades by mathematicians and ex-physicists in the field of statistics in econometrics. We think that many phenomena exhibiting power-law behavior are not necessarily the consequence of a nonextensivity of the entropy as this has been assumed by a number of authors, myself [64] -[66] included, evoking exotic form of the entropy. The same results can be obtained using the BSM density function and taking account of the difference in the definition of the exponents (Equation (6)). In our presentation nonextensivity, when it occurs, it is the consequence of the scale dependence of the characteristic exponents a and c of the distribution and is a property of systems with long range interactions and complex systems, where thermodynamic equilibrium is not achieved.
Cite this paper
F.Brouers, (2015) The Burr XII Distribution Family and the Maximum Entropy Principle: Power-Law Phenomena Are Not Necessarily “Nonextensive”. Open Journal of Statistics,05,730-741. doi: 10.4236/ojs.2015.57073
References
- 1. Burr, I.W. (1942) Cumulative Frequency Functions. The Annals of Mathematical Statistics, 13, 215-232.
http://dx.doi.org/10.1007/s10463-011-0342-9 - 2. Singh, S. and Maddala, G. (1976) A Function for the Size Distribution of Income. Econometrica, 44, 963-970.
http://dx.doi.org/10.1007/s10985-005-2970-y - 3. Park, S.Y. and Bera, A.K. (2007) Maximum Entropy Income Densities with an Application to the U.S. Personal Income Data. Working Paper, University of Illinois, Urbana-Champaign.
http://dx.doi.org/10.1007/s11634-008-0025-4 - 4. Park, S.Y. and Bera, A.K. (2009) Maximum Entropy Autoregressive Conditional Heteroskedasticity Model. Journal of Econometrics, 150, 219-230.
http://dx.doi.org/10.1007/s10463-009-0239-z - 5. Papalexiou, S.M. and Koutsoyiannis, D. (2012) Entropy Based Derivation of Probability Distributions: A Case Study to Daily Rainfall. Advances in Water Resources, 45, 51-57.
http://dx.doi.org/10.1007/s12561-009-9000-7 - 6. McDonald, J.B. (1984) Some Generalized Functions for the Size Distribution of Income. Econometrica: Journal of the Econometric Society, 52, 647-663.
http://dx.doi.org/10.1007/s10255-011-0093-7 - 7. Ferriani, F. (2015) Traders and Time: Who Moves the Market? Studies in Economics and Finance, 32, 74-97.
http://dx.doi.org/10.1016/j.jmva.2005.03.002 - 8. Girard, S. and Guillou, A. (2015) Reduced-Bias Estimator of the Conditional Tail Expectation of Heavy-Tailed Distributions. In: Editor, Ed., Mathematical Statistics and Limit Theorems, Springer International Publishing, 105-123.
http://dx.doi.org/10.3150/bj/1137421639 - 9. Streftaris, G., Waters, H.R. and Stott, A.D. (2015) The Effect of Model Uncertainty on the Pricing of Critical Illness Insurance. Annals of Actuarial Science, 9, 108-133.
- 10. Ducey, M.J. and Gove, J.H. (2015) Size-Biased Distributions in the Generalized Beta Distribution Family, with Applications to Forestry. Forestry, 88, 143-151.
http://dx.doi.org/10.1006/jmva.2001.2012 - 11. Brouers, F. (2014) Statistical Foundation of Empirical Isotherms. Open Journal of Statistics, 4, 687-701.
http://dx.doi.org/10.4236/ojs.2014.49064 - 12. Brouers, F. and Al-Musawi, T.J. (2015) On the Optimum Use of Isotherm Model for the Characterization of Biosorption of Lead onto Algae. Journal of Molecular Liquids, 212, 46-51.
http://dx.doi.org/10.1016/j.molliq.2015.08.054 - 13. Brouers, F. and Sotolongo-Costa, O. (2006) Generalized Fractal Kinetics in Complex Systems (Application to Biophysics and Biotechnology). Physica A: Statistical Mechanics and Its Applications, 368, 165-175.
http://dx.doi.org/10.1016/j.physa.2005.12.062 - 14. Hamissa, A.M.B., Brouers, F., Mahjoub, B. and Seffen, M. (2007) Adsorption of Textile Dyes Using Agave americana (L.) Fibres: Equilibrium and Kinetics Modelling. Adsorption Science and Technology, 25, 311-325.
http://dx.doi.org/10.1260/026361707783432533 - 15. Ncibi, M.C., Mahjoub, B., Seffen, M., Brouers, F. and Gaspard, S. (2009) Sorption Dynamic Investigation of Chromium (VI) onto Posidonia oceanic Fibres: Kinetic Modelling Using New Generalized Fractal Equation. Biochemical Engineering Journal, 46, 141-146.
http://dx.doi.org/10.1016/j.bej.2009.04.022 - 16. Figaro, S., Avril, J.P., Brouers, F., Ouensanga, A. and Gaspard, S. (2009) Adsorption Studies of Molasse’s Wastewaters on Activated Carbon: Modelling with a New Fractal Kinetic Equation and Evaluation of Kinetic Models. Journal of Hazardous Materials, 161, 649-656.
http://dx.doi.org/10.1016/j.jhazmat.2008.04.006 - 17. Hamissa, A.B., Brouers, F., Ncibi, M.C. and Seffen, M. (2013) Kinetic Modeling Study on Methylene Blue Sorption onto Agave americana Fibers: Fractal Kinetics and Regeneration Studies. Separation Science and Technology, 48, 2834-2842.
http://dx.doi.org/10.1080/01496395.2013.809104 - 18. Debord, J., Bollinger, J.C., Bordas, F., Harel, M. and Dantoine, T. (2013) Microcalorimetric Study of the Inhibition of Butyrylcholinesterase by Sodium Arsenite and Zinc Chloride: Use of a Fractal Kinetic Model. Thermochimica Acta, 561, 49-53.
http://dx.doi.org/10.1016/j.tca.2013.03.027 - 19. Kyzas, G.Z., Deliyanni, E.A. and Lazaridis, N.K. (2014) Magnetic Modification of Microporous Carbon for Dye Adsorption. Journal of Colloid and Interface Science, 430, 166-173.
http://dx.doi.org/10.1016/j.jcis.2014.05.049 - 20. Brouers, F. (2014) The Fractal (BSf) Kinetics Equation and Its Approximations. Journal of Modern Physics, 5, 1594-1598.
http://dx.doi.org/10.4236/jmp.2014.516160 - 21. Pereira, L.M. (2010) Fractal Pharmacokinetics. Computational and Mathematical Methods in Medicine, 11, 161-184.
http://dx.doi.org/10.1080/17486700903029280 - 22. Weron, K. and Kotulski, M. (1997) On the Equivalence of the Parallel Channel and the Correlated Cluster Relaxation models. Journal of Statistical Physics, 88, 1241-1256.
http://dx.doi.org/10.1007/BF02732433 - 23. Brouers, F. and Sotolongo-Costa, O. (2005) Relaxation in Heterogeneous Systems: A Rare Events Dominated Phenomenon. Physica A: Statistical Mechanics and Its Applications, 356, 359-374.
http://dx.doi.org/10.1016/j.physa.2005.03.029 - 24. Abubakar, M., Aliyu, A.B. and Ahmad, N. (2015) Flexural Strength Analysis of Dense and Porous Sintered Clay Using Weibull Probability Distribution. Applied Mechanics and Materials, 761, 347-351.
http://dx.doi.org/10.4028/www.scientific.net/AMM.761.347 - 25. Tu, J.W., Guo, D.L., Mei, S.T., Jiang, H.C. and Li, X.P. (2015) Three-Parameter Weibull Distribution Model for Tensile Strength of GFRP Bars Based on Experimental Tests. Materials Research Innovations, 19, S5-1191-S5-1196.
http://dx.doi.org/10.1179/1432891714z.0000000001276 - 26. Bütikofer, L., Stawarczyk, B. and Roos, M. (2015) Two Regression Methods for Estimation of a Two-Parameter Weibull Distribution for Reliability of Dental Materials. Dental Materials, 31, e33-e50.
http://dx.doi.org/10.1016/j.dental.2014.11.014 - 27. Nadler, D.L. (2015) Developing a Weibull Model Extension to Estimate Cancer Latency Times. Doctoral Dissertation, State University of New York at Albany, Albany.
- 28. Goutelle, S., Maurin, M., Rougier, F., Barbaut, X., Bourguignon, L., Ducher, M. and Maire, P. (2008) The Hill Equation: A Review of Its Capabilities in Pharmacological Modelling. Fundamental and Clinical Pharmacology, 22, 633-648.
http://dx.doi.org/10.1111/j.1472-8206.2008.00633.x - 29. Hill Keller, F., Schröppel, B. and Ludwig, U. (2015) Pharmacokinetic and Pharmacodynamics Considerations of Antimicrobial Drug Therapy in Cancer Patients with Kidney Dysfunction. World Journal of Nephrology, 4, 330-344.
http://dx.doi.org/10.5527/wjn.v4.i3.330 - 30. Chou, T.C. (1976) Derivation and Properties of Michaelis-Menten Type and Hill Type Equations for Reference Ligands. Journal of Theoretical Biology, 59, 253-276.
http://dx.doi.org/10.1016/0022-5193(76)90169-7 - 31. Bhaskaran, S., Umesh, P. and Nair, A.S. (2015) Hill Equation in Modeling Transcriptional Regulation. In: Singh, V. and Dhar, P.K., Eds., Systems and Synthetic Biology, Springer, Dordrecht, 77-92.
http://dx.doi.org/10.1007/978-94-017-9514-2_5 - 32. Criado, M.N., Civera, M., Martínez, A. and Rodrigo, D. (2015) Use of Weibull Distribution to Quantify the Antioxidant Effect of Stevia rebaudiana on Oxidative Enzymes. LWT-Food Science and Technology, 60, 985-989.
http://dx.doi.org/10.1016/j.lwt.2014.10.041 - 33. Oral, F., Ekmekçi, I. and Onat, N. (2015) Weibull Distribution for Determination of Wind Analysis and Energy Production. World Journal of Engineering, 12, 215-220.
http://dx.doi.org/10.1260/1708-5284.12.3.215 - 34. Brouers, F., Sotolongo, O., Marquez, F. and Pirard, J.P. (2005) Microporous and Heterogeneous Surface Adsorption Isotherms Arising from Levy Distributions. Physica A: Statistical Mechanics and Its Applications, 349, 271-282.
http://dx.doi.org/10.1016/j.physa.2004.10.032 - 35. Ncibi, M.C., Altenor, S., Seffen, M., Brouers, F. and Gaspard, S. (2008) Modelling Single Compound Adsorption onto Porous and Non-Porous Sorbents Using a Deformed Weibull Exponential Isotherm. Chemical Engineering Journal, 145, 196-202.
http://dx.doi.org/10.1016/j.cej.2008.04.001 - 36. Yuhn, K.H., Kim, S.B. and Nam, J.H. (2015) Bubbles and the Weibull Distribution: Was There an Explosive Bubble in US Stock Prices before the Global Economic Crisis? Applied Economics, 47, 255-271.
http://dx.doi.org/10.1080/00036846.2014.969824 - 37. Sornette, D. (2003) Critical Phenomena in Natural Sciences. 2nd Edition, Chap. 14, Springer, Heidelberg.
- 38. Reinyi, A. (1970) Probability Theory. North-Holland Publishing Company, Amsterdam.
- 39. Tsallis, C. (1988) Possible Generalization of Boltzmann-Gibbs Statistics. Journal of Statistical Physics, 52, 479-487.
http://dx.doi.org/10.1007/BF01016429 - 40. Tsallis, C. (2009) Nonadditive Entropy and Nonextensive Statistical Mechanics—An Overview after 20 Years. Brazilian Journal of Physics, 39, 337-356.
http://dx.doi.org/10.1590/S0103-97332009000400002 - 41. Kapur, J. and Kesavan, H. (1992) Entropy Optimization Principles with Applications. Academic Press, Waltham.
http://dx.doi.org/10.1007/978-94-011-2430-0_1 - 42. Wu, X. (2003) Calculation of Maximum Entropy Densities with Application to Income Distribution. Journal of Econometrics, 115, 347-354.
http://dx.doi.org/10.1016/S0304-4076(03)00114-3 - 43. Rathie, P.N. and Da Silva, S. (2008) Shannon, Lévy, and Tsallis: A Note. Applied Mathematical Sciences, 2, 1359-1363.
- 44. Kafri, O. (2009) The Distributions in Nature and Entropy Principle. arXiv:0907.4852.
- 45. Papalexiou, S.M. and Koutsoyiannis, D. (2011) Entropy Maximization, p-Moments and Power-Type Distributions in Nature. European Geosciences Union General Assembly 2011, Geophysical Research Abstracts, Vol. 13, Vienna, 03-08 April 2011, European Geosciences Union, EGU2011-6884.
- 46. Mahmoud, M.R. and El Ghafour, A.S.A. (2013) Shannon Entropy for the Generalized Feller-Pareto (GFP) Family and Order Statistics of GFP Subfamilies. Applied Mathematical Sciences, 7, 3247-3253.
- 47. Peterson, J., Dixit, P.D. and Dill, K.A. (2013) A Maximum Entropy Framework for Nonexponential Distributions. Proceedings of the National Academy of Sciences of the United States of America, 110, 20380-20385.
http://dx.doi.org/10.1073/pnas.1320578110 - 48. Visser, M. (2013) Zipf’s Law, Power Laws and Maximum Entropy. New Journal of Physics, 15, Article ID: 043021.
http://dx.doi.org/10.1088/1367-2630/15/4/043021 - 49. Freundlich, U. (1906) Uber Die Adsorption in Losungen. Journal of physical chemistry, 57, 385-470.
- 50. Kopelman, R. (1988) Fractal Reaction Kinetics. Science, 241, 1620-1626.
http://dx.doi.org/10.1126/science.241.4873.1620 - 51. Savageau, M.A. (1995) Michaelis-Menten Mechanism Reconsidered: Implications of Fractal Kinetics. Journal of Theoretical Biology, 176, 115-124.
http://dx.doi.org/10.1006/jtbi.1995.0181 - 52. van den Broek, J. and Nishiura, H. (2009) Using Epidemic Prevalence Data to Jointly Estimate Reproduction and Removal. The Annals of Appliedstatistics, 3, 1505-1520.
http://dx.doi.org/10.1214/09-aoas270 - 53. Verhulst, P.F. (1845) Nouveaux Mémoires de l’Académie des Sciences, des Arts et des Beaux Arts de Belgique. Vol. 18.
- 54. Ausloos, M. and Dirickx, M. (Eds.) (2006) The Logistic Map and the Route to Chaos: From the Beginnings to Modern Applications. Springer Science and Business Media, Berlin.
http://dx.doi.org/10.1007/3-540-32023-7 - 55. Havriliak, S. and Negami, S. (1967) A Complex Plane Representation of Dielectric and Mechanical Relaxation Processes in Some Polymers. Polymer, 8, 161-210.
http://dx.doi.org/10.1016/0032-3861(67)90021-3 - 56. Langmuir, I. (1918) The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. Journal of the American Chemical Society, 40, 1361-1403.
http://dx.doi.org/10.1021/ja02242a004 - 57. Sips, R. (1948) The Structure of a Catalyst Surface. The Journal of Chemical Physics, 16, 490-495.
http://dx.doi.org/10.1063/1.1746922 - 58. Jurlewicz, A. and Weron, K. (1999) A General Probabilistic Approach to the Universal Relaxation Response of Complex Systems. Cellular and Molecular Biology Letters, 4, 55-86.
- 59. Stanislavsky, A. and Weron, K. (2013) Is There a Motivation for a Universal Behaviour in Molecular Populations Undergoing Chemical Reactions? Physical Chemistry Chemical Physics, 15, 15595-15601.
http://dx.doi.org/10.1039/c3cp52272e - 60. Rodriguez, R.N. (1977) A Guide to the Burr Type XII Distributions. Biometrika, 64, 129-134.
http://dx.doi.org/10.1093/biomet/64.1.129 - 61. Brouers, F. (2013) Sorption Isotherms and Probability Theory of Complex Systems. arXiv:1309.5340.
- 62. Kapur, J.N. (1989) Maximum-Entropy Models in Science and Engineering. John Wiley and Sons, New York.
- 63. Beck, C. (2002) Non-Additivity of Tsallis Entropies and Fluctuations of Temperature. Europhysics Letters (EPL), 57, 329-333.
http://dx.doi.org/10.1209/epl/i2002-00464-8 - 64. Brouers, F., Sotolongo-Costa, O. and Weron, K. (2004) Burr, Lévy, Tsallis. Physica A: Statistical Mechanics and Its Applications, 344, 409-416.
http://dx.doi.org/10.1016/j.physa.2004.06.008 - 65. Brouers, F. and Sotolongo-Costa, O. (2003) Universal Relaxation in Nonextensive Systems. Europhysics Letters (EPL), 62, 808-814.
http://dx.doi.org/10.1209/epl/i2003-00444-0 - 66. Brouers, F., Sotolongo-Costa, O., Gonzalez, A. and Pirard, J.P. (2005) Entropic Origin of Dielectric Relaxation Universalities in Heterogeneous Materials (Polymers, Glasses, Aerogel Catalysts). Physica Status Solidi (C), 2, 3529-3531.
http://dx.doi.org/10.1002/pssc.200461736


