Open Journal of Statistics
Vol.05 No.05(2015), Article ID:58778,14 pages
10.4236/ojs.2015.55045
Simultaneous Optimization of Incomplete Multi-Response Experiments
Pradip Kumar Nandi, Rajender Parsad, Vinod Kumar Gupta
ICAR-IASRI, Library Avenue, Pusa, New Delhi, India
Email: nandi_stat@yahoo.co.in, rajender.parsad@icar.gov.in, vkgupta@iasri.res.in
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 May 2015; accepted 10 August 2015; published 13 August 2015
ABSTRACT
This article attempts to develop a simultaneous optimization procedure of several response variables from incomplete multi-response experiments. In incomplete multi-response experiments all the responses (p) are not recorded from all the experimental units (n). Two situations of multi-response experiments considered are (i) on 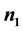 units all the responses are recorded while on
units all the responses are recorded while on 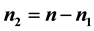 units a subset of
units a subset of 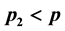 responses is recorded and (ii) on
responses is recorded and (ii) on 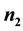 units all the responses (p) are recorded, on
units all the responses (p) are recorded, on 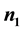 units a subset of
units a subset of 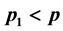 responses is recorded and on
responses is recorded and on  units the remaining subset of
units the remaining subset of 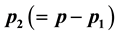 responses is recorded. The procedure of estimation of parameters from linear multi-response models for incomplete multi-response experiments has been developed for both the situations. It has been shown that the parameter estimates are consistent and asymptotically unbiased. Using these parameter estimates, simultaneous optimization of incomplete multi-response experiments is attempted following the generalized distance criterion [1] . For the implementation of these procedures, SAS codes have been developed for both complete (k ≤ 5, p = 5) and incomplete (k ≤ 5, p1 = 2, 3 and p2 = 2, 3, where k is the number of factors) multi-response experiments. The procedure developed is illustrated with the help of a real data set.
responses is recorded. The procedure of estimation of parameters from linear multi-response models for incomplete multi-response experiments has been developed for both the situations. It has been shown that the parameter estimates are consistent and asymptotically unbiased. Using these parameter estimates, simultaneous optimization of incomplete multi-response experiments is attempted following the generalized distance criterion [1] . For the implementation of these procedures, SAS codes have been developed for both complete (k ≤ 5, p = 5) and incomplete (k ≤ 5, p1 = 2, 3 and p2 = 2, 3, where k is the number of factors) multi-response experiments. The procedure developed is illustrated with the help of a real data set.
Keywords:
Incomplete Multi-Response Experiments, Simultaneous Optimization, Response Surface Designs, Ridge Analysis

1. Introduction
The experimental situations where more than one response is observed for a set of input combinations are known as multi-response experiments. In these experiments, experimenter is interested in determining the optimum combination of input factors. There are several experimental situations in which simultaneous optimization of several response variables is required. For example, in food processing experiments, a food technologist may be interested in determining the optimum combinations of various ingredients of a product or operability conditions for obtaining the product on the basis of acceptability, colour, flavour, nutritional value, economic and biochemical parameters, etc. Such experimental situations do exist in many other disciplines of science. For some more such experimental situations, a reference may be made to [2] . The experiments for simultaneous optimization of several responses are generally conducted in response surface designs. The determination of the conditions on the set of input variables that simultaneously optimize a multi-response function is of particular interest.
Multi-response optimization is the process of determining a combination of levels of input factors that yield optimal values of several response variables taken simultaneously. In such experimental situations, one should not obtain the optima for each response variable separately. When more than one response variables are under investigation simultaneously, the meaning of optimum combination becomes unclear since there is no unique way to order multivariate values of a multi-response function. Further the conditions that are optimal for one response variable may be far from optimal or may even be physically impractical for the other response variables. Therefore, the procedure of simultaneous optimization of several response variables is required. In the literature, different procedures for simultaneous optimization of several responses have been suggested (see e.g. [1] [3] - [7] ).
[4] and [1] considered an optimization problem associated with a dual response system consisting of two responses. [3] and [6] adopted desirability function approach for optimization of complete multi-response experiments. [1] gave an optimization procedure based on minimization of generalized distance. The above procedures are suitable only for the situations where the process is optimized either for maximization of all response variables or minimization of all the response variables.
There, however, do occur experimental situations particularly in osmotic dehydration studies where one wants to optimize the process keeping in view the maximum moisture loss and minimum solids gain. Such a situation has also been encountered by [8] . Hence, there is a need to develop a procedure of optimization where optimum conditions for maximization of some of the response variables and minimization of the remaining response variables is desired. It is, therefore, suggested that we take the negative values of the response variables to be minimized and determine the optimum combination using the procedure of maximization of all the response variables.
The above discussion relates to the experimental situations, where the data on all the response variables are collected from each design point. In some experimental situations, it may not be possible to observe data on all the response variables from all the experimental units. The data from only a subset of responses are collected from some experimental units and other subset of responses from other experimental units. Some of the responses may be common to two or more experimental units. For example, consider an experiment on modified atmospheric packaging (MAP) conducted to determine the optimum combinations of temperature, packaging material and time on the basis of different physical parameters like physiological loss of weight (PLW), moisture content (MC) and texture; biochemical parameters like total sugars, flavanoids and total soluble solids (TSS); microbiological parameters like, total count and caliform count and sensory parameters like, colour, flavour and overall acceptability. In such situations it may happen that after some days, the data on a subset of parameters such as sensory may not be available due to spoilage of the packaged food material for some of the treatment combinations. In this particular situation, the data on sensory characters may not be available at 25 degree centigrade after 11 days for the packaging material HDPE (High Density polyethylene). Further, it may be possible to record the data on all the response variables in some of the replications of the treatment combinations due to variability in the raw material and their differences in initial microbial count.
In response surface designs generally some of the design points are replicated for testing the lack of fit. Due to constraints on time or equipments, it may not be possible to collect data on all the response variables from each of the replicated design points. Therefore, the experimenter may divide the response variables in as many groups as the replications of a design point. Some of the response variables are common in each of the sets. Therefore, this is also an incomplete multi-response situation, where simultaneous optimization of several response variables is required.
Cold storage studies involving different temperatures may also encounter such situations. Field experiments where certain plots or treatment combinations are affected by pests or insects may also have situations as described above. For example, if a field crop is affected by insects/pests which affect only the leaf and damage it, we may be able to record data on other response variables but not on the response variables related to leaf or say if the grain/pod is affected and damaged, we may not be able to record data on yield but can record physical and other parameters like plant height etc.
From the above discussion we can see that there are two types of multi-response experiments viz. complete multi-response and incomplete multi-response experiments where interest is in simultaneous optimization of several response variables. As mentioned above, some procedures of simultaneous optimization of several response variables are available for complete multi-response situations. These procedures are involved quite algebraically, therefore, for the benefit of experimenters it is required to develop some computer based procedure for simultaneous optimization of several response variables.
For incomplete multi-response situations, it seems that no analytical procedure for simultaneous optimization of several response variables is available in the literature. The basic difference between simultaneous optimization from complete and incomplete multi-response experiments is in estimation of parameters in multi-response equations. As shown in [2] that in complete multi-response situations, the parameter estimates are same as that of the estimates obtained from fitting response surfaces individually for all the response variables. This, however, may not be the case with incomplete multi-response situations. Therefore, in the present investigation an attempt has been made to obtain the parameter estimates for the data obtained from incomplete multi-response experiments. Once the parameter estimates are obtained, the procedure of simultaneous optimization given by [1] has been used.
In Section 2, the procedure of estimation of parameters from incomplete multi-response experiments is developed. Two situations of incomplete multi-response considered are (i) on 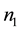 units all the p responses are recorded while on
units all the p responses are recorded while on 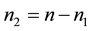 units a subset of
units a subset of 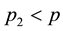 responses is recorded and (ii) on
responses is recorded and (ii) on 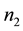 units all the responses (p) are recorded, on
units all the responses (p) are recorded, on  units a subset of
units a subset of 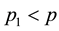 responses is recorded and on
responses is recorded and on 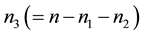 units the remaining subset of
units the remaining subset of 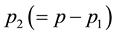 responses is recorded. In Section 3, a stepwise procedure of simultaneous optimization of complete/incomplete multi-response is described in brief. The procedure of parameter estimation and obtaining simultaneous optima is illustrated with the help of examples in Section 4. SAS codes have been developed for the whole procedure for both complete (k ≤ 5, p = 5) and incomplete (k ≤ 5, p1 = 2, 3 and p2 = 2, 3, where k is the number of factors) multi-response experiments. The codes are available with the first author and can be obtained by sending an E-mail to nandi_stat@yahoo.co.in.
responses is recorded. In Section 3, a stepwise procedure of simultaneous optimization of complete/incomplete multi-response is described in brief. The procedure of parameter estimation and obtaining simultaneous optima is illustrated with the help of examples in Section 4. SAS codes have been developed for the whole procedure for both complete (k ≤ 5, p = 5) and incomplete (k ≤ 5, p1 = 2, 3 and p2 = 2, 3, where k is the number of factors) multi-response experiments. The codes are available with the first author and can be obtained by sending an E-mail to nandi_stat@yahoo.co.in.
2. Parameter Estimation from Incomplete Multi-Response Experiments
In this section, we develop an estimation procedure of parameters of linear multi-response models for incomplete multi-response situations. We consider two cases for incomplete multi-response as described in the sequel.
2.1. Case I
Let there be p (= p1 + p2) response variables which are measured for each design point of k input variables (factors)
For the first p1 response variables, model can be written as

where
yi: n1 ´ 1 vector of observations on the ith response variable,
Xi: n1 ´ m matrix of rank m of known functions of the settings of the coded variables,
bi: m ´ 1 vector of unknown constant parameters, and ei: n1 ´ 1 vector of random error associated with the ith response variable
Model for each of the remaining p2 response variables is

yj: (n1 + n2) ´ 1 vector of observations on the jth response variable,
Figure 1. Lengths of bars represent number of observation recorded for that response.
Xj: (n1 + n2) ´ m matrix of rank m of known functions of the settings of the coded variables,
bj: m ´ 1 vector of unknown constant parameters, and ej: (n1 + n2) ´ 1 vector of random error associated with the jth response variable
Now combining and rolling down the models (1) and (2) we have


where Y1 is (n1p1 ´ 1) vector of observations on p1 response variables, 


Here, Xi = X1 

Using the above, the design matrix Z is






The vector of parameters is

where b1(mp1 ´ 1) is the vector of parameters for first p1 response variables and b2(mp2 ´ 1) is the vector of parameters for remaining p2 response variables. So b is the vector of parameters of order (mp1 + mp2) ´ 1. Similarly, one can also write the expression for residual vectors as

where e1 is (n1p1 ´ 1) vector of residuals for first p1 response variables, 

From the structure of residual vector, the dispersion matrix of residual vector is

As is clear from (8) that the covariance between p1 and p2 can only be possible on n1 observations and for n2 observations covariance cannot be obtained (zero). In (8) 


It may be noted here that the form of Z in (5) with unequal number of observations for each set of responses (n1 for p1 and n1+n2 for p2 response variables), requires additional effort to estimate

Asymptotically unbiased estimator of b is

The dispersion matrix of 

Equations (10) and (11) require knowledge of



Estimation of b When W Is Unknown
It is easy to prove that if we replace 


Let E1 (n1 ´ p1) and E2 ((n1 + n2) ´ p2) be the matrices of least-squares residuals for the p1 and p2 response variables respectively. E2 can be partitioned analogously to X2 and Y2 as

Now we define the following quantities:

The consistent estimators of 

Once a consistent estimator of 



The dispersion matrix of 

Following the proof of [10] , one can easily see that the estimators of b in (15) have distributions which are symmetric around the true value of b and their mean exists. These are, therefore, unbiased.
2.2. Case-II
Let there be p (=p1 + p2) response variables which are measured for each design point of k input variables (factors)



For the first p1 response variables, model can be written as

where
yi: (n1 + n2) ´ 1 vector of observations on the ith response variable,
Xi: (n1 + n2) ´ m matrix of rank m of known functions of the settings of the coded variables,
bi: m ´ 1 vector of unknown constant parameters, and ei : (n1 + n2) ´ 1 vector of random error associated with
Figure 2. Lengths of bars represent number of observations recorded for that response.
the ith response variable
Model for each of the remaining p2 response variables is

where
yj: (n2 + n3) ´ 1 vector of observations on the jth response variable,
Xj: (n2 + n3) ´ m matrix of rank m of known functions of the settings of the coded variables,
bj: m ´ 1 vector of unknown constant parameters, and ej: (n2 + n3) ´ 1 vector of random error associated with the jth response variable
Now combining and rolling down the models (17) and (18) we have
where,









where Y, b and e are column vectors with




We now regard the above model as a single equation regression model and making use of Aitken’s GLS technique asymptotically unbiased estimator of 






Estimation of b When W Is Unknown
In most of the practical situation 




Let E1 ((n1 + n2) ´ p1) and E2 ((n2 + n3) ´ p2) be the matrices of least-squares residuals for the p1 and p2 response variables respectively. Ei’s can be partitioned analogously to Yi and Xi in (19) and (20)

Now we define the following quantities:

The consistent estimators of 

Once a consistent estimator of 




As in Case I, following the proof of [10] , one can easily see that the estimators of b based on the estimators given in (27) have distributions which are symmetric around the true value of b and their mean exists. They are, therefore, unbiased.
3. Simultaneous Optimization Procedures
In the present study, simultaneous optimization of several responses based on minimization of generalized distance given by [1] has been considered. SAS codes have been developed for the whole procedure for both complete (k ≤ 5, p = 5) and incomplete (k ≤ 5, p1 = 2, 3 and p2 = 2, 3, where
For the sake of completeness, we describe the procedure in brief. Using the parameter estimates obtained in Section 2, the prediction equation for the ith response at design point 

where 



Combining all the response variables together we can get the prediction equation at design point 


where 
Let 


and let
then an “ideal” optimum is said to be achieved. The problem of multi-response optimization is, therefore, obviously solved and no further work is needed. However, such an ideal optimum may rarely exist. In more general situations one might consider finding compromising conditions on the input factors that are somewhat favorable to all responses. Such a deviation of the compromising conditions from the ideal optimum is formulated by means of a distance function, which measures the distance of 


where 


The above distance function is termed as generalized distance by [1] . The multi-response optimization then involves finding the optimum point x that minimize this generalized distance function (33) over the experimental
region W. If x0 is the point in the experimental region at which 
and if m0 is the value of this minimum, then one may describe the experimental conditions at x0 as being near optimal for each of the p response functions. The smaller the value of m0, the closer these conditions are to representing an “ideal” optimum. To summarize, the steps for obtaining a simultaneous optima of a multi-response function consisting of p responses are:
1) Obtain the predicted equations using the complete/incomplete multi-response data and the method of generalized least squares.
2) Choose a distance measure 
3) Optimize the predicted responses individually over the experimental region W to obtain the vector 

4) The distance measure being a function of x alone is minimized over W.
Here the controlled random search procedure given in [12] can be employed effectively.
The results of ridge analysis for optimization of individual responses can be obtained using PROC RSREG in SAS [13] by simply using the RIDGE MAX statement to the RSREG SAS code. But for incomplete multi-response situation one can’t use this procedure. So to obtain individual optima for incomplete multi-response situation a SAS code has been developed for determining individual optima using the method of ridge analysis for determining optima. The SAS code can be used for specified number of input factors (k ≤ 5) and response variables (p1 = 2, 3 and p2 = 2, 3). The SAS code is available with the first author and can be obtained by sending an E-mail to nandi_stat@yahoo.co.in. The method of ridge analysis for determining optimum conditions given in [2] is used for the purpose of obtaining individual optima of the response variables with incomplete observations.
4. Illustrations
In this section, we illustrate the procedure developed in Sections 2 and 3 for simultaneous optimization of several response variables through the data from a quantitative factorial experiment.
Example 4.1: An experiment was conducted on osmotic dehydration of banana to determine the optimum combinations of power levels, temperature and air velocity at Division of Agricultural Engineering, ICAR- Indian Agricultural Research Institute, New Delhi. The levels of the 3 factors tried are shown in Table 1.
The data were collected on energy use efficiency (%)





where xi is the coded variable, 


The coded levels of the factors and data on 5 response variables in given in Table 3.
As mentioned in Section 1 that in case of complete multi-response situations, the parameter estimates obtained by taking all the response variables together is same as obtained individually for each of the response variables. A second order response surface model was fitted to each of the 5 response variables separately to obtain the parameter estimates. The regression coefficient estimates, their standard errors, and the coefficients of determination
It was observed that stationary points are outside the experimental region for some of the response variables, we have performed ridge analysis to obtain individual maxima. The individual maxima for the 5 response
Table 1. Factors and levels.
Table 2. Coded factors and levels.
Table 3. Design points in coded levels of input factors and response values.
Table 4. Least squares fit and regression estimates.
*The number in the parentheses is the standard error.
variables obtained by the method of ridge analysis are given in Table 5. Using the distance measure given in (33)
simultaneous maxima for the 5 response variables is obtained by minimizing

2.48, 71.63, 54.48, 643.65) and the results are given in Table 6. The location at which the linear complete multi-response function attains its simultaneous minima is [0.995 (278.95 W), 0.59 (46.55˚C), −0.52 (0.98 m/s)] and the corresponding maxima (41.02, 2.55, 71.22, 54.51, 643.16) for the response variables. The minimum value of the distance function obtained is 3.81.
Now, to illustrate the procedure for incomplete multi-response situations, we have deleted the data on some of the response variables on some of the design points in Example 4.1. Example 4.2 relates to Case I of incomplete multi-response situation as discussed in Section 2.1.
Example 4.2: For the purpose of illustration, consider the experiment in Example 4.1 for complete multi-response experiments. Let us consider that the data on Energy use efficiency (%), Rehydration ratio and TSS for the design points (1, 1, 0) and (1, 1, 1) at serial number 35 and 36 in Table 3 are deleted.
In case of incomplete multi-response experiments the parameter estimates obtained by taking each response variable individually is not same as the parameter estimates obtained taking all the response together. In this case to estimate the parameters of the second order response surface are obtained as per procedure of Case I in Section 2.1. After obtaining individual estimates based on the available data, residuals are used to obtain variance-covariance matrix. Using the variance-covariance matrix, we have obtained the GLS estimate of the parameters of the second order response surface model. Comparing Table 4 and Table 7 it can be observed that, parameter estimates of the response variables with incomplete data on some design points are different.
It was observed that the stationary points are outside the experimental region for some of the response variables, we have performed ridge analysis to obtain individual maxima. Table 8 includes the individual maxima for the five response variables obtained by the method of ridge analysis. Using the distance measure given in (33)
simultaneous maxima for the 5 response variables is obtained by minimizing

2.50, 71.72, 54.49, 643.68)' and the results are given in Table 9. From the results on individual maxima it can be observed that, individual maxima obtained from the incomplete data on three response variables on some design points are different from that obtained with complete multi-response data.
The location at which the linear incomplete multi-response function attains its simultaneous optima is [1.000 (280 W), 0.610 (57.2˚C), −0.470 (1.03 m/s)] and the corresponding maxima (40.70, 2.57, 71.42, 54.55, 643.76) for the response variables are given in Table 9. It can also be observed that the minimum value of the distance
Table 5. The individual Maxima.
Table 6. Simultaneous optimum combination of input factors.
*Actual value of optimum point is given in parenthesis.
Table 7. The Generalized least squares fit and regression estimates.
*The number in the parentheses is the standard error.
Table 8. The individual maxima.
Table 9. Simultaneous optimum combination of input factors.
*Actual value of optimum point is given in parenthesis.
function obtained is 3.36 which is lower (3.81) than that obtained from complete multi-response situation as given in Table 9.
On the similar lines, one can obtain the simultaneous optima for Case II of incomplete multi-response situations.
5. Conclusion
In the present investigation, a methodology was developed for estimation of parameters and optimization of simultaneous optimization from multi-response experiments where some responses could not be obtained on some design points. The procedure of obtaining a consistent estimator of unknown dispersion matrix in case of incomplete multi-responses is also suggested. The simultaneous optimization procedure is implemented through SAS codes for specified number of input factors (k ≤ 5) and response variables (p1 = 2, 3 and p2 = 2, 3). The procedures developed have been illustrated through an example. Further efforts are required to obtain a general procedure for any number of factors and any number of response variables in incomplete multi-response situations.
Acknowledgements
Authors are thankful to Dr Abhijit Kar for sharing the data that has been used for illustration in Section 4. The authors are also thankful to reviewer and the editor for their valuable suggestions that led to improvements in the presentation of the results. The present article is part of Ph.D. work of first author.
Cite this paper
Pradip KumarNandi,RajenderParsad,Vinod KumarGupta, (2015) Simultaneous Optimization of Incomplete Multi-Response Experiments. Open Journal of Statistics,05,430-444. doi: 10.4236/ojs.2015.55045
References
- 1. Khuri, A.I. and Conlon, M. (1981) Simultaneous Optimization of Multiple Responses Represented by Polynomial Regression Functions. Technometrics, 23, 363-375.
http://dx.doi.org/10.1080/00401706.1981.10487681 - 2. Khuri, A.I. and Cornell, J.A. (1996) Response Surfaces: Designs and Analyses. 2nd Edition, Marcel Dekker, New York.
- 3. Harrington, E.C. (1965) The Desirability Function. Industrial Quality Control, 21, 494-498.
- 4. Myers, R.H. and Carter Jr., W.H. (1973) Response Surface Techniques for Dual Response Systems. Technometrics, 15, 301-317.
http://dx.doi.org/10.1080/00401706.1973.10489044 - 5. Biles, W.E. (1975) A Response Surface Method for Experimental Optimization of Multi-Response Processes. Industrial and Engineering Chemistry Process Design and Development, 14, 152-158.
http://dx.doi.org/10.1021/i260054a010 - 6. Derringer, G. and Suich, R. (1980) Simultaneous Optimization of Several Response Variables. Journal of Quality Technology, 12, 214-219.
- 7. Conlon, M. and Khuri, A.I. (1990) MR: Multiple Response Optimization. Report No. 322, Department of Statistics, University of Florida, Gainesville, FL.
- 8. Kar, A., Chandra, P., Parsad, R., Samuel, D.V.K. and Khurdiya, D.S. (2001) Osmotic Dehydration of Banana (Dwarf Cavendish) Slices. Indian Journal of Agricultural Engineering, 38, 12-21.
- 9. Schimdt, P. (1977) Estimation of Seemingly Unrelated Regressions with Unequal Number of Observations. Journal of Econometrics, 5, 365-377.
http://dx.doi.org/10.1016/0304-4076(77)90045-8 - 10. Kakwani, N.C. (1967) The Unbiasedness of Zellner’s Seemingly Unrelated Regression Equations Estimator. Journal of the American Statistical Association, 62, 141-142.
http://dx.doi.org/10.1080/01621459.1967.10482895 - 11. Sharma, V.K. (1993) Estimation of Seemingly Unrelated Regressions with Unequal Numbers of Observation. Sankhya, B 55, 135-138.
- 12. Price, W.L. (1977) A Controlled Random Search Procedure for Global Optimization. Computer Journal, 20, 367-370.
http://dx.doi.org/10.1093/comjnl/20.4.367 - 13. SAS Institute Inc. (1989) SAS/STAT User’s Guide. Vol. 2, Version 6, 4th Edition, Cary, NC.






