Open Journal of Statistics
Vol.05 No.01(2015), Article ID:54179,8 pages
10.4236/ojs.2015.51009

Forecasting High-Frequency Long Memory Series with Long Periods Using the SARFIMA Model

Handong Li, Xunyu Ye

School of Government, Beijing Normal University, Beijing, China

Email: lhd@bnu.edu.cn, xunyuye@bnu.edu.cn

Copyright © 2015 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 25 January 2015; accepted 13 February 2015; published 17 February 2015

ABSTRACT

This paper evaluates the efficiency of the SARFIMA model at forecasting high-frequency long memory series with especially long periods. Three other models, the ARFIMA, ARMA and PAR models, are also included to compare their forecasting performances with that of the SARFIMA model. For the artificial SARFIMA series, if the correct parameters are used for estimating and forecasting, the model performs as well as the other three models. However, if the parameters obtained by the WHI estimation are used, the performance of the SARFIMA model falls far behind that of the other models. For the empirical intraday volume series, the SARFIMA model produces the worst performance of all of the models, and the ARFIMA model performs best. The ARMA and PAR models perform very well both for the artificial series and for the intraday volume series. This result indicates that short memory models are competent in forecasting periodic long memory series.

Keywords:

High-Frequency Financial Series, Long Memory, Long Periods, SARFIMA, Monte Carlo Simulation, Intraday Volume

1. Introduction

Recent years have witnessed a vast increase in the amount of high-frequency financial market data that are available. Using these data, practitioners are now able to manage their assets in greater detail. For example, the intraday volume series is often used in the Volume Weighted Average Price (VWAP) strategy to avoid a large reverse impact when executing large orders. Consequently, the econometrics of the high-frequency financial series receives wider attention in the academic field. As Engle (2005) summarizes, intraday financial series often contain periodic patterns and present a long horizon of strong dependence [1] . The autocorrelation function (ACF) of these series decays slowly and is particularly significant at the seasonal lags. These periods can be especially long when the sampling interval becomes short.

A number of works have been concerned with forecasting the periodic long memory series. They mainly focused on forecasting series with relatively short periods, namely twelve monthly periods or four seasonal periods in a year. On one hand, various long memory models have been used for forecasting this series. An autoregressive fractionally integrated moving average (ARFIMA) model [2] [3] was directly applied by Franses & Ooms (1997) in [4] to forecast quarterly UK inflation. Porter-Hudak (1990) suggested a seasonal autoregressive fractionally integrated moving average (SARFIMA) model to forecast monetary aggregates [5] . This model tries to remove the hyperbolic decay at the seasonal lags by including a seasonal fractional differencing filter

in the ARFIMA model, where B is the backward shift operator, s is the given period and D is the

seasonal differencing parameters. This model is later used in [6] for monthly river flows and in [7] for inflation rates. By introducing seasonal dummy variables to seasonally change the fractional differencing parameter in the ARFIMA model, Ref. [4] proposed a periodic ARFIMA (PARFIMA) model for forecasting periodic long memory series. On the other hand, short memory models, such as the autoregression (AR) model and the periodic autoregression (PAR) model, were also proven to be competent in handling this series.

However, no consistent conclusion has been made on the superiority of specific models for forecasting periodic long memory series. Franses & Ooms (1997) [4] tried the periodic PAR model, AR model, PARFIMA model and ARFIMA model to forecast the quarterly UK inflation, but found no significant difference between these models. Those authors did find that the PARFIMA model was generally outperformed by rival models. Porter-Hudak (1990) compared the SARFIMA model and the Airline model, and found that the former outperformed the latter [5] . Nasr & Trabelsi (2005) tried the PARFIMA, SARFIMA, PAR, and AR models in [7] to forecast inflation rates in four different countries, and showed that the long memory models, the PARFIMA model and the SARFIMA model, performed better than the short memory models in terms of information criteria and clean residuals.

This paper studies the performance of different models when forecasting high-frequency long memory series with long periods. In particular, we want to deduce whether the SARFIMA model is capable of forecasting this type of series, because the mechanism of the SARFIMA process fits the description of the periodic long memory series well. Artificial SARFIMA series are generated to test the performance of different forecasting models, including the ARFIMA, the SARFIMA, the AR and the PAR models. We are also interested in finding a suitable model for forecasting intraday volume series, which is a very useful series for VWAP trading. These four models will also be tried on this series for comparison.

This paper is organized as follows: Section 2 introduces the four forecasting models that will be tested. Section 3 studies the performances of the four models through Monte Carlo simulations. Section 4 uses these models to forecast the intraday volume in both the American and Chinese stock markets and then compares their performance. Section 5 presents our conclusion.

2. The Models

2.1. Long Memory Models

Two long memory models will be used in our study. The ARFIMA model ignores periodicity. The other, the SAFARMA model, includes periodicity.

If we assume that a simple fractional differencing operator can remove the high autocorrelation at both the seasonal lags and non-seasonal lags, we can use an ARFIMA model directly to help forecast a periodic long memory series. The ARFIMA model is defined as:

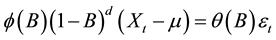
where 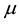is the mean of the process, is the white noise process, B is the backward shift operator, 0 < d < 0.5 is the differencing parameters respectively, 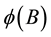, 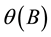are the polynomial operators with orders p, q respectively.

A full definition of the SARFIMA 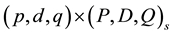model is defined as:

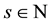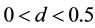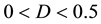where is the seasonal period, and are the non-seasonal and seasonal differencing parameters respectively, with additional constraints 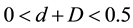to assure the stationary of the process, 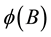, 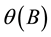are the non-seasonal polynomial operators with orders p, q respectively, , are the seasonal polynomial operators with orders P, Q respectively:

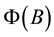For convenience, this paper is restricted to the SARFIMA model with, namely:

and the ARFIMA model with.

For the ARFIMA model, there are several methods chosen for its parameter estimation, including the Exact Maximum Likelihood method [8] , WHI method [9] and Non-Linear Least Squares estimator [10] . For the SARFIMA model, Reisen et al. (2006) suggest a maximum likelihood method for its estimation [11] . However, this method is time-consuming when calculating the covariance matrix, especially for the high-frequency series with a relatively large sample size and when the AR coefficients, MA coefficients, seasonal and non-seasonal fractionally differencing parameters are all nonzero. Moreover, no further improvement for simplifying the procedure of this method, such as what Sowell (1991) does to improve the maximum likelihood estimation for the ARFIMA model, has yet been proposed. Bisognin & Lopes (2007) use the WHI method for the SARFIMA model’s estimation in [12] . This method is simpler and faster in application. Because this paper discusses the forecasting of large sample high-frequency data using the SARFIMA model with nonzero AR and MA coefficients and non-seasonal fractionally differencing parameters, we use the WHI method for estimating the SARFIMA model.

For consistency, this paper also uses the WHI method to estimate the parameters of the ARFIMA. WHI is an approximated likelihood method. The discrete form of its likelihood function is given by:

where is the vector of unknown parameters, is the frequency, n is the sample size,

is the spectral density function of and

2.2. Short Memory Models

The two short memory models used in this paper are the ARMA model and the PAR model.

The ARMA model is formulated as:

By incorporating seasonal polynomial operators to the AR model, the PAR(p) model is defined as:

where s is the given period and is the seasonal polynomial operators with orders P:

This paper is restricted with, namely an ARMA (1,1) and a PAR(1). The parameters of the AR and PAR models are estimated by non-linear least squares method.

3. Simulation Study

To test the performance of different models for forecasting a periodic long memory series, we generate the SARFIMA artificial series with zero mean and unit variance:

when, when, autoregressive and moving average parameters and fractional differencing parameters. Periods are used to correspond to the periods of the intraday volume series examined in the next section. Consequently, there are four types of this artificial series. The last two periods of each series are left for forecasting; the former data are used for estimation. Forecasts are undertaken one-step in advance. For example, for {s = 48, n = 300} series, the 1st to 204th real data are used for estimation so that we can obtain the 205th predictive data. Then, the 2nd to 205 real data are used for estimation, and we forecast the 206th predictive data. Under each sample size, 100 duplicated series are generated to investigate the overall forecasting performance of different models. Figure 1 plots the examples of the last two periods of the four types of the artificial series. Figure 2 shows the ACF of these four series.

The periodicity does not seem to be apparent for all of these series, but the ACF shows significant autocorrelations both at the seasonal and non-seasonal lags for the two series. The Augmented Dickey-Fuller unit root test and two semiparametric tests, GPH test and the Gaussian Semi-parametric (GSP) test [13] [14] are also undertaken to examine their stationary status and long memory. Table 1 lists the ADF unit root test and the long

Figure 1. Data plots for the artificial series, the 205th to 300th data for n = 300 series (left), the 1005th to 1100th data for n = 1100 series (right).

Figure 2. ACF for the artificial series, n = 300 series (left), n = 1100 series (right).

Table 1. ADF and long memory test results.

*Significant at 5% level.

memory test results. The ADF and long memory tests show that the two series are both stationary and with significant long memory.

For other duplicated series, their plots, ACF, stationarity and long memory properties are similar with the two series examined above. Due to space constraints, we provide only two examples here and do not elaborate on them.

The four models are then used to forecast the artificial series for testing their forecasting performances. Two sets of parameters are used for forecasting, especially for the SARFIMA model. One parameter is obtained by the WHI estimation. The other, as we already know the true parameters of the artificial SARFIMA series, is the set of parameters of the artificial series. Accordingly, we can take the performance of these two different parameter settings for the WHI estimation together to determine whether estimation bias would cause any negative effect. The statistical measure used in this paper for measuring forecasting accuracy is the mean squared error of the estimators (MSE), given by:

where k is the number of predicted data and and are the real and predictive value of the series respectively. For each type within the artificial series, we calculate the average MSE of the 100 duplicated series by:

Table 2 lists the average MSE of the four models for forecasting the four types of the artificial series. The SARFIMA model with known parameters is denoted as SARFIMA-known. The SARFIMA model with parameters estimated by WHI is denoted as SARFIMA-WHI. The averages of the MSE of these models for the 100 duplicated series are listed in the last row.

First, we can see from Table 2 that the PAR model performs best at forecasting all types of the artificial series. Its MSE are the smallest for most duplicated series. This finding indicates that a periodic short memory model is competent at predicting an SARFIMA series. The SARFIMA model using known parameters also performs well, with its average MSE ranked second. The non-periodic models, namely the ARFIMA and ARMA models, perform slightly worse than the periodic models. This finding indicates that considering periodicity is beneficial for accurately forecasting the artificial SARFIMA series, but the differences between the performances of the PAR, ARMA, SARFIMA-known and ARFIMA models are not very large. The differences of their average MSE are within 0.06.

However, the performance of SARFIMA-WHI falls significantly behind that of other models. Most of its MSE are much larger than that of others. Table 3 lists the average of the estimated parameters for the SAR- FIMA-WHI model.

We can see that the WHI method tends to underestimate both the seasonal and non-seasonal fractional differencing parameters d and D. This phenomenon is true especially for the n = 300 artificial series, for which the WHI method underestimate d and D by nearly 0.1. This finding indicates that the estimation bias is responsible for the loss of forecasting accuracy of the SARFIMA model using the WHI estimation.

4. Empirical Study

The intraday volume series is a very useful series for VWAP trading strategy, which splits and executes orders according to the predicted intraday volume distribution. Intraday volume series is a typical series that presents both periodicity and long memory. Here, we choose data gathered from the NASDAQ composite index and the

Table 2. The average MSEs for forecasting four types of the artificial series.

Table 3. The average of the estimated parameters for the SARFIMA-WHI model.

Shanghai Stock Exchange 50 Index (SSE 50 Index)1 to populate the sample for this description. We use two one-month samples. The SSE 50 Index ranges from January 4th to 31st 2011 in 5-minute intervals. The NASDAQ sample ranges from January 3rd to 31st 2011 in 5-minute intervals. Because the trading time for the Chinese stock market is 4 hours per day and for the American stock market is 6.5 hours per day, the total time of every trading day can be divided into 48 parts and 78 parts, respectively. Therefore, for 20 trading days, we obtained 960 and 1560 observed values from the Chinese market and American market, respectively. For each 5-minute interval, volume means the sum of all volumes traded within 5 minutes. Figure 3 shows the plots and the ACF of the sample series.

The periodicity and slow decay of the intraday volume series seem to be much more apparent than the artificial SARFIMA series. The plots show that the sample of the intraday volume series of the SSE 50 Index and NASDAQ composite index fluctuate in a U-shape and presents an apparent 48 and 78 periods, respectively. The ACF of the series show a very slow decay in the autocorrelation function both at the seasonal and non-seasonal lags for the series.

Next, we apply the four models to a one-year sample of the SSE 50 Index and NASDAQ composite index intraday volume to investigate their forecasting performance. This is an in-sample forecast comparison. The parameters of the models are estimated every month. The forecast is undertaken one-step ahead, using the monthly fixed parameters and historical rolling five-day data to forecast the next data. Table 4 and Table 5 list the statistics of the mean, maximum value, minimum value, ADF t-statistics and fractional differencing parameters d estimated by GPH and GSP of the SSE 50 Index and NASDAQ composite index intraday volume for each month in 2011, respectively.

On average, the maximum value of each month is more than 4 times the mean value and more than 28 times the minimum value. This finding indicates a large deviation, partly due to the seasonal pattern. Although the ADF tests prove these series all to be stationary, most of the two semi-parametric estimators of the fractional differencing parameter, GPH and GSP, are near or above 0.5. These rates indicate that these stationary series have very strong long memories.

Applying the four models to the sample intraday volume series, we obtain the statistics of MSE of their forecasting, as listed in Table 6 and Table 7.

The results of the two tables are fairly similar. For most monthly samples, the ARFIMA model performs best, indicating that a fractional differencing is beneficial for forecasting intraday volume series. Meanwhile, the non- periodic models, the ARFIMA and the ARMA, seem to be superior to the periodic models. This finding indicates that, for forecasting intraday volume, adding periodicity may be unnecessary or redundant in terms of forecasting accuracy. The worst performance belongs to the SARFIMA model, of which the MSE are highest for forecasting all monthly samples. We can conclude that although this model is considered to be theoretically suitable for modeling periodic long memory series, it does not actually work very well on our intraday volume

Figure 3. The plots and the ACF of the SSE 50 Index, January 4th to 31st 2011, 5-minute intervals.

Table 4. The statistics of the SSE 50 Index intraday volume for each month in 2011.

*Significant at 5% level.

Table 5. The statistics of the NASDAQ intraday volume for each month in 2011.

*Significant at 5% level.

Table 6. The MSE (×1010) of the four models’ forecasting results, SSE 50 Index.

In the column “Performance”, “>” means to be superior to, e.g. ARFIMA > ARMA means the ARFIMA model is superior to the ARMA model for forecasting the corresponding months’ intraday volume.

Table 7. The MSE (×102) of forecasting results, NASDAQ composite index.

In the column “Performance”, “>” means to be superior to, e.g. ARFIMA > ARMA means the ARFIMA model is superior to the ARMA model for forecasting the corresponding months’ intraday volume.

samples. Additionally, the two short memory models, the ARMA and PAR models, perform slightly worse than the ARFIMA model, but much better than the SARFIMA model does. This finding indicates that the short memory models are also competent in forecasting intraday volume.

5. Conclusions

This paper evaluates the performance of the SARFIMA model at forecasting periodic long memory series, including the artificial SARFIMA series, the SSE 50 Index intraday volume series and NASDAQ composite index volume series. Three other models are also included in our study to compare their forecasting performances with that of the SARFIMA model.

For the artificial SARFIMA series, if we use the correct parameters for estimating and forecasting, it performs well relative to the other three models. However, if we use the parameters obtained by the WHI estimation, the forecasting performance of this model falls considerably behind other models. This phenomenon may be partly due to the estimation bias of the WHI estimation, which tends to underestimate both the seasonal and non-sea- sonal fractional differencing parameters. The PAR model performs best at forecasting all four artificial series. Meanwhile, the non-periodic models, namely the ARFIMA and ARMA models, do not perform as well as the periodic models. This outcome indicates that considering periodicity is beneficial for forecasting the artificial SARFIMA series.

For the intraday volume series, the ARFIMA model performs the best among all the models, indicating that fractional differencing is beneficial for forecasting the intraday volume series. For most monthly samples, the non-periodic models, the ARFIMA model and the ARMA model, seem to be superior to the periodic models. This outcome indicates that, for forecasting intraday volume, adding periodicity may be unnecessary or redundant in terms of forecasting accuracy. The SARFIMA model does not work very well on our intraday volume samples, exhibiting the worst performance among all the models used. In addition, the two short memory models, the ARMA and PAR models, also performed well compared to the SARFIMA model.

In summary, the SARFIMA was outperformed by other rival models in our study. Combining the results of the simulation and empirical study together, we conclude that the poor performance of the SARFIMA model may be caused by the inaccurate estimation obtained by the WHI method. The estimation method for this model still needs further improvement. Before more effective and more accurate estimation methods are proposed, we suggest that the SARFIMA model should be carefully applied when forecasting a high-frequency long memory time series with long periods.

References

  1. Engle, R. (2005) Handbook of Financial Econometrics. North Holland, Amsterdam.
  2. Granger, C.W.J. and Joyeux, R. (1980) An Introduction to Long-Memory Time Series Models and Fractional Differencing. Journal of Time Series Analysis, 1, 15-29. http://dx.doi.org/10.1111/j.1467-9892.1980.tb00297.x
  3. Hosking, J.R.M. (1981) Fractional Differencing. Biometrika, 68, 165-176. http://dx.doi.org/10.1093/biomet/68.1.165
  4. Franses, P.H. and Ooms, M. (1997) A Periodic Long-Memory Model for Quarterly UK Inflation. International Journal of Forecasting, 13, 117-126. http://dx.doi.org/10.1016/S0169-2070(96)00715-7
  5. Porter-Hudak, S. (1990) An Application of the Seasonal Fractionally Differenced Model to the Monetary Aggregates. American Statistical Association, 85, 338-344. http://dx.doi.org/10.1080/01621459.1990.10476206
  6. Ooms, M. and Franses, P.H. (2001) A Seasonal Periodic Long Memory Model for Monthly River Flows. Environmental Modeling & Software, 16, 559-569. http://dx.doi.org/10.1016/S1364-8152(01)00025-1
  7. Nasr, A.B. and Trabelsi, A. (2005) Seasonal and Periodic Long Memory Models in the Inflation Rates. European Financial Management Association 2005 Annual Meetings, 31.
  8. Sowell, F. (1992) Maximum Likelihood Estimation of Stationary Univariate Fractionally Integrated Time Series Models. Journal of Econometrics, 53, 165-188. http://dx.doi.org/10.1016/0304-4076(92)90084-5
  9. Whittle, P. (1953) Estimation and Information in Stationary Time Series. Arkiv för Matematik, 2, 423-434. http://dx.doi.org/10.1007/BF02590998
  10. Doornik, J.A. and Ooms, M. (2004) Inference and Forecasting for ARFIMA Models, with an Application to US and UK Inflation. Studies in Nonlinear Dynamics and Econometrics, 8, 1218. http://dx.doi.org/10.2202/1558-3708.1218
  11. Reisen, V.A., Rodrigues, A.L. and Palma, W. (2006) Estimation of Seasonal Fractionally Integrated Processes. Computational Statistics & Data Analysis, 50, 568-582. http://dx.doi.org/10.1016/j.csda.2004.08.004
  12. Bisognin, C. and Lopes, S.R.C. (2007) Estimating and Forecasting the Long-Memory Parameter in the Presence of Periodicity. Journal of Forecasting, 26, 405-427. http://dx.doi.org/10.1002/for.1030
  13. Geweke, J. and Porter-Hudak, S. (1983) The Estimation and Application of Long Memory Time Series Models. Journal of Time Series Analysis, 4, 221-238. http://dx.doi.org/10.1111/j.1467-9892.1983.tb00371.x
  14. Robinson, P.M. (1995) Log Periodogram Regression of Time Series with Long Range Dependence. Annals of Statistics, 23, 1048-1072. http://dx.doi.org/10.1214/aos/1176324636

NOTES

1The SSE 50 Index used consists of the 50 largest stocks of good liquidity and representativeness from the Shanghai security market according to an objective, scientific method.

Journal Menu >>