Received 4 October 2014; revised 2 November 2014; accepted 18 November 2014

ABSTRACT

The exponential weighted moving average technique used in process mean and variance monitoring charts was combined by Gan in 1997 and proposed two combined joint monitoring schemes one with rectangular control region and the other with elliptical control region. Performance of these two schemes may very depend on the shifts in mean or variance to be detected quickly. In this paper, performances of these two schemes are evaluated with respect to the average run length properties. The results reveal that elliptical scheme is little faster in detecting the shifts in process mean and increase in variance within a limit.

Keywords:

Average Run Length, Exponential Weighted Moving Average, Joint Monitoring

1. Introduction

Exponential weighted moving average (EWMA) chart for monitoring a shift in process mean was introduced by Roberts in 1959 and the design procedure of EWMA mean charts was reported by Crowder in 1989 [1] [2] . Later Chang and Gan showed that EWMA chart can also be used to monitor the sample variance [3] . However, Gan emphasized the importance of jointly monitoring the mean and variance, as that process monitoring is a bivariate problem [4] [5] . The current practice of joint monitoring scheme consists of a mean and a variance chart to look a bivariate problem using two univariate procedures. Two combined joint monitoring schemes using EWMA charts with a rectangular control region (EE_r) and an elliptical control region (EE_e) were proposed by Gan [4] . When there is more than one scheme for joint monitoring, it is needed to compare the performances of the schemes under different scenarios. The performance of individual EWMA chart was studied using its run length distribution by Crowder, Lucas and Saccucci [6] [7] . In this paper the performance of the EE_r and EE_e schemes is evaluated different scenarios based on average run length (ARL) properties. ARL is defined as the average number of samples taken until an out-of-control signal is issued in quality control schemes.

2. Methodology

An EWMA chart for monitoring the sample mean is obtained by plotting 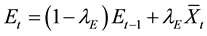against the sample number t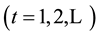, where E₀ is usually set at target mean µ₀, l_E is a constant such that 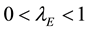and it is selected based on the shift in the mean to be detected quickly. An out-of-control signal is issued if 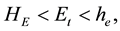where H_E and h_E are the upper control limit and lower control limit respectively. The EWMA chart for monitoring the sample variance 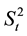can be obtained by plotting 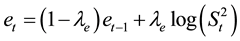against the sample number t, where e₀ is usually set at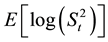, l_e is a positive constant such that 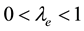and it is selected based on the shift in the variance to be detected quickly. An out-of-control signal is issued if e_t is greater than the H_e or e_t is less than the h_e. H_e and h_e are the upper and lower control limits respectively for the EWMA variance chart.

In the EE_r scheme, EWMA mean chart and the EWMA variance chart are combined by plotting the EWMA of 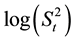against the EWMA of. The upper and lower control limits of the two charts form four sides of a rectangular control region. In EE_e scheme, the distance from the point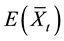, 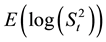will decide whether a point falls inside the elliptical control region or not. This distance is calculated using Hotelling type statistics T² for each sample. The quantity 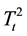for a point in which e_t is greater than 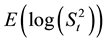is given as

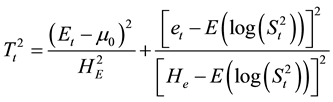(1)

and for a point in which e_t is less than, is given as

(2)

Figure 1 illustrates the difference between the rectangular and elliptical control regions in which point B is an in-control point with respect to the EE_r scheme, but it is an out-of control point with respect to the EE_e scheme. Similarly, point A is an out-of-control point with respect to the EE_r scheme, but it is an in-control point with respect to the EE_e scheme. In process monitoring, both the magnitude of the shift and the direction are important and therefore it advisable to plot the individual samples.

Simulated data set were used for comparing the performance of the two combined schemes. For this simulation, the in-control mean (µ₀) and variance are assumed to be 0 and 1 respectively with sample size 5. This means each sample comprises 5 normally distributed observations. The optimal parameters for constructing these schemes were obtained for two commonly used ARLs 250 and 370 and rechecked by simulation performed in SAS using proc RANNO. Simulations were run until the standard error of the ARL was less than 1% of the pre-specified ARL. The control chart parameters of these two schemes for in-control ARL’s of 250 and 370 are given in Table 1.

The performances of the schemes are compared based on out of control ARLs when there is a shift in mean or variance or in both. Schemes detect various magnitudes of shifts in mean and variance based on their sensitivities. The scheme which gives smaller ARL when there is a shift in mean or variance is the better scheme. The shifts in mean and variance investigated are given by

(3)

and

(4)

where The process is in-con- trol when ∆ = 0.0 and δ = 1.00 and otherwise the process has changed. For each scheme and each combination 1,000,000 runs were performed to estimate the out-of-control ARL. The standard deviations of run length (SDRL) values were ensured that SDRL were less than 1% of the estimated ARL. For making the comparison, a comparison efficiency index is introduced:

(5)

where,

= Comparative efficiency of a scheme for ∆ shift in mean and δ shift in variance;

= ARL for ∆ shift in mean and δ shift in variance;

= Minimum ARL observed among EE_r and EE_e schemed for a ∆ shift in mean and a δ shift in variance for particular in-control ARL.

3. Results and Discussion

Table 2 and Table 3 shows the out-of-control ARLs for different magnitudes of shifts in mean and variance for in-control ARLs of 250 and 370. Figure 2 and Figure 3 compare the efficiency of the two schemes using the index. According to the Table 2 and Table 3, in general, the EE_r scheme performs very similar with EE_e scheme. Figure 2 and Figure 3 shows when δ > 1, EE_e scheme detect the shifts quicker than the EE_r scheme. However this property is lost when ∆ > 1.5 but it does not harm because after ∆ > 1.5 both schemes detect the shifts very quickly. When δ < 1, EE_e scheme gives larger out-of-control ARLs compare to the EE_r scheme and therefore index for EE_e scheme is smaller compare to EE_r scheme. This is a good property because decrease in variance is always favored. The design procedure of these schemes can be introduced through software for industrial use so that it can be a readymade scheme.

4. Conclusion

In overall the EE_e scheme is faster than the EE_r scheme in detecting the shifts in process mean and variance but the design procedure of EE_e scheme is little complex due to its complex equations. Further less variance is signaled slowly in the EE_e schemes compare to EE_r scheme which is a preferred characteristic. Therefore EE_e scheme outperformed the EE_r scheme.

Acknowledgements

This work was supported by the South Eastern University of Sri Lanka and the Higher Education for the Twenty First Century Project, Sri Lanka [SEUSL/O-AS/N1].

References