Received 24 July 2014; revised 8 August 2014; accepted 19 August 2014

ABSTRACT

In this paper maximum ranked set sampling procedure with unequal samples (MRSSU) is proposed. Maximum likelihood estimator and modified maximum likelihood estimator are obtained and their properties are studied under exponential distribution. These methods are studied under both perfect and imperfect ranking (with errors in ranking). These estimators are then compared with estimators based on simple random sampling (SRS) and ranked set sampling (RSS) procedures. It is shown that relative efficiencies of the estimators based on MRSSU are better than those of the estimator based on SRS. Simulation results show that efficiency of proposed estimator is better than estimator based on RSS under ranking error.

Keywords:

Efficiency, Error in Ranking, Maximum Likelihood Estimator, Modified Maximum Likelihood Estimator, Ranked Set Sampling

1. Introduction

In many studies where sampling is used, such as environmental managements, ecology, sociology and agriculture, exact measurement of a selected unit is either difficult or costly and time-consuming. However, the ranking of a small set of selected units can be carried out easily either by visual inspection with respect to the study variable or on the basis of auxiliary variable. McIntyre [1] proposed a method, later called ranked set sampling (RSS), for estimating mean pasture and forage yields when measurement is costly. In RSS one first draws m² units at random from the population and partitions them into m sets of m units. The m units in each set are ranked without making actual measurements. From the first set of m units the unit ranked lowest is chosen for actual quantification. From the second set of m units the unit ranked second lowest is measured. This process is continued until the unit ranked largest is measured from the m-th set of m units. If a large sample is required then the procedure can be repeated r times to obtain a sample of size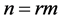. These chosen elements are called ranked set sample. Dell and Clutter [2] and Takahasi and Wakimoto [3] studied theoretical aspects of this technique on the assumption of perfect judgment ranking and imperfect judgment ranking, respectively. Dell and Clutter [2] showed that the variance of the ranked set sample mean is never larger than the variance of the random sample mean, whether or not judgment ranking is perfect (for more research work on parametric methods for RSS, see for example, Lam et al. [4] , Stokes [5] ). Samwi et al. [6] used extreme ranked set sample (ERSS) which is easier to use than RSS procedure to estimate the population mean in case of symmetric distributions. Al-Odat and Al-Saleh [7] introduced concept of varied set size RSS which they called moving extreme ranked set sampling (MERSS).

Al-Saleh and Al-Hadhrami [8] studied the MLE of location distributions based on MERSS. Abu-Dayyeh and Al-Sawi [9] have obtained modified MLE of the mean of exponential distribution using MERSS. The MERSS requires identification of 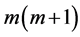sample units and 2m of these are actually measured, thus making a comparison of this sampling procedure with RSS of size m is meaningless. In the next section we introduce a maximum ranked set sampling procedure with unequal samples. The existence of MLE for scale parameter of exponential distribution is demonstrated and properties are studied in Section 3. Since under some regularity conditions the asymptotic efficiency of the MLE can be obtained from the inverse of the Fisher information number, we compute Fisher information number for scale parameter in Section 4. The asymptotic efficiency of the MLE using proposed sampling scheme w.r.t. that using SRS and RSS is compared numerically for the scale parameter of the exponential distribution in this section. In order to get a closed form expression of the approximate MLE of, some terms of the likelihood equation will be replaced by their expectations. This technique was used by Mehrotra and Nanda [10] for studying MLE based on censored data, Zheng and Al-Saleh [11] for MLE with RSS data, and Al-Saleh and Al-Hadhrami [8] [12] and Abu-Dayyeh and Al-Sawi [9] for MLE using MERSS data. In Section 5 we study a modified MLE for estimating the scale parameter of exponential distribution assuming perfect ranking. Numerical comparison of these estimators is given here. Errors in ranking are studied in Section 6.

2. Maximum Ranked Set Sampling with Unequal Samples (MRSSU)

In the maximum ranked set sampling with unequal samples (MRSSU), we draw m simple random samples, where the size of the i-th sample is i,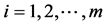. The procedure of MRSSU is described as follows

1) Select m SRS of size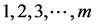, respectively.

2) Order the element of each set by visual inspection or other relatively inexpensive methods, without actual measurement of the characteristic of interest.

3) Measure accurately the maximum ordered observation from each set.

4) Repeat the above steps r times until the desired sample size 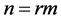is obtained.

In MRSSU, we measure accurately only m maximum order statistics out of 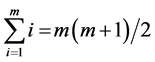ranked units.

Since it is not difficult to identify maximum in each set. MRSSU is a very useful modification of RSS. It allows for an increase in set size without introducing too many ranking errors.

3. The Maximum Likelihood Estimator

Assume that the characteristic of interest X has a probability density function 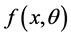and distribution function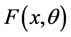, where the form of F is known, our interest is to estimate 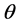based on MRSSU. Let, be m sets of random samples from X, and they are independent. Denote ,. Then is a MRSSU from X. Note that the elements of this sample are independent. If the judgment ranking is perfect then 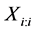has the same density as the i-th order statistic (maximum) of an SRS of size i from, i.e., has the density

The likelihood function based on MRSSU can be written as

The log-likelihood function is

where C is a constant. Let a MRSSU be drawn from an exponential distribution with pdf, , and hence taking the first derivative of w.r.t., we have

(1)

If the MLE of exists, then it is a solution of. The MLE of denoted by, which satisfies

(2)

Now, taking second derivative we have

(3)

Note that the first term of Equation (3) is always negative and the second term is zero at any solution of Equation (2). Thus. The left hand side (LHS) of Equation (2) is a continuous function of

. When, the LHS of (2) goes to and when, the LHS of Equation (2) goes to.

Thus the solution of (2) exists. Thus Equation (2) has a unique solution and this solution is MLE of. From Equation (2), we get the MLE, which can be obtained iteratively.

Theorem 1. Assume that we are sampling from an exponential distribution using MRSSU then for any real number “a” satisfies

1)

2)

Proof. Proof of this theorem is similar to Theorem 1 of Chen et al. [13] .

4. The Fisher Information Number

We denote the MLE’s based on SRS by and RSS by, respectively. In order to compare the performance of estimator based on MRSSU w.r.t. SRS and RSS, we need to study the asymptotic efficiency of w.r.t. and, respectively. Since under some regularity conditions (see Lehmann [14] (pp. 440-441)) the asymptotic efficiency of the MLE can be obtained from the inverse of the Fisher information number, we consider the Fisher information number of the scale parameter in this section.

If satisfies regularity conditions, the Fisher number in X is

We give the Fisher information number based on MRSSU in the following theorem.

Theorem 2. With for, the Fisher information number based on MRSSU of size m is given by

(4)

Proof. From Equation (1), we have

Note that

(5)

After simplification Equation (5) reduces to Equation (4).

We compare the ML estimator from the SRS which is, where and the ML estimator

from the RSS which is obtained from Equation (2.6) of [5] denoted by which satisfies

(6)

where denote the i-th order statistics from i-th set of RSS with size m. The Fisher information about based on SRS is

(7)

From [5] Fisher information number about is given by

(8)

Asymptotic efficiency of MLE using MRSSU w.r.t. that of using SRS is defined as

(9)

Similarly, we have

(10)

The numerical results are shown in Table 1. ARE of w.r.t. is greater than 1 and increases with m. ARE of w.r.t. is greater than 1 for and decreases as m increases for. This is because RSS of the same size m uses more ranked units than MRSSU of the same size, for example RSS of size 5 uses 25 ranked units, whereas MRSSU of the same size uses only 15 ranked units.

5. Modified MLE (MMLE)

In order to obtain closed form approximate MLE of, the last term of LHS of likelihood Equation (2) is replaced by its expectation. The idea of replacing the hazard rate in the maximum likelihood equation by its expectation was proposed by Mehrotra and Nanda [10] , who estimated parameters of normal and gamma distributions based on Type II censored data. This technique used by Zheng and Al-Saleh [11] for obtaining MLE of location and scale parameters based on RSS.

Taking the expectation of third term of LHS of (2), we obtain

After simplification, we get likelihood Equation (2) as

Solving for, we have

(11)

where

is called modified MLE of.

Theorem 3.

a) is unbiased estimator of.

b) (12)

where d is defined as in Equation (11).

Proof a). From Equation (11), we have

i.e.,

(13)

It is well known that under some regularity conditions (see Lehmann [14] (pp. 440-441)),. We can see that expectation of third term of Equation (2) simplifies to

(14)

Using Equation (13) and Equation (14), the expectation of Equation (2) reduces to

(15)

Hence the proof of a).

Proof b). Since is the i-th order statistics of a SRS of size i from the exponential distribution, with parameter, the pdf of is given by

(16)

Now

(17)

Thus using Equation (17), we obtain Equation (12).

We compare MMLE based on MRSSU relative to MLE using SRS and MMLE using RSS with the same size. From Equation (2.6) of Zheng and Al-Saleh [11] we can obtain MMLE of scale parameter of exponential distribution using RSS and is given by

where is as defined in (6) and

We can easily derive the variance of and is given by

Let represents efficiency of MMLE based on MRSSU w.r.t. based on SRS is given by

Similarly, efficiency of relative to MMLE based on RSS is given by

The efficiencies were computed for and are presented in Table 2. Note that the efficiency between any two of these estimators do not depend on and these values were computed only for. From Table 2 it can be seen that computed efficiencies increases as the sample size m increases. From values we observed that estimator based on MRSSU are as efficient as estimator based on RSS for sample size, and then decreases for.

6. Errors in Ranking

In this section we study the situation where there are ranking errors. For MRSSU the ranking may not always be perfect, i.e., i-th largest observation in the i-th set measured by MRSSU method may not be the actual i-th largest order statistics in the set of size i. The errors in ranking may have an effect on the estimates.

To gain some insight of the effect of ranking errors on the efficiencies of the estimators, various simulation

trails were conducted. We use the simulation method considered by David and Lavine [15] and Dell and Clutter [2] . In the first stage we generate m sets of simple random samples, from the exponential distribution with scale parameter. The corresponding m sets of random error variables, were generated from normal distribution with mean zero and variance. Define

where X_ij and e_ij are independent. Then we can obtain MRSSU’s of X_ij’s and Z_ij’s (,). The sets of , are ranked with respect to the first components of. The second components are taken as judgment ranked order statistics and they constitute MRSSU’s with judgment error unless, ,. We compute estimators based on judgment ranked MRSSU’s.

We repeat this procedure for 10,000 times. The estimate for is the average of the estimates from these replications, and variance of the estimate is the sample variance. Similarly using 10,000 simulated samples the RSS and SRS procedures were used to obtain the values of estimators of and their sampling variances. The simulated estimators based on RSS with imperfect ranking and SRS are denoted by and. The efficiency and the expected value of the modified MLE have been computed by using R-software, version 3.0.2. The results are presented in Tables 3-5.

It is observed from Table 3 that bias in the modified ML estimator ranges from 0.0002 to 0.1065, i.e., estimator based on is very close to true parameter. Based on Table 4 we can easily observe that the efficiency of the estimator based on w.r.t. estimator based on is larger than 1 and increases with m and

decreases with in the presence of ranking error. From Table 5 it can be seen that modified MLE based on w.r.t. is larger than 1 and increases with m and in the presence of ranking error. This indicates that modified MLE based on MRSSU is better than modified MLE in the presence of ranking error.

References