Open Journal of Statistics
Vol.4 No.5(2014), Article ID:49085,7 pages
DOI:10.4236/ojs.2014.45040
Efficiency of the Adaptive Cluster Sampling Designs in Estimation of Rare Populations
Charles Mwangi*, Ali Islam, Luke Orawo
Department of Mathematics, Egerton University, Nakuru, Kenya
Email: *charlesmwangi59@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 July 2014; revised 3 August 2014; accepted 11 August 2014
Abstract
Adaptive cluster sampling (ACS) has been a very important tool in estimation of population parameters of rare and clustered population. The fundamental idea behind this sampling plan is to decide on an initial sample from a defined population and to keep on sampling within the vicinity of the units that satisfy the condition that at least one characteristic of interest exists in a unit selected in the initial sample. Despite being an important tool for sampling rare and clustered population, adaptive cluster sampling design is unable to control the final sample size when no prior knowledge of the population is available. Thus adaptive cluster sampling with data-driven stopping rule (ACS’) was proposed to control the final sample size when prior knowledge of population structure is not available. This study examined the behavior of the HT, and HH estimator under the ACS design and ACS’ design using artificial population that is designed to have all the characteristics of a rare and clustered population. The efficiencies of the HT and HH estimator were used to determine the most efficient design in estimation of population mean in rare and clustered population. Results of both the simulated data and the real data show that the adaptive cluster sampling with stopping rule is more efficient for estimation of rare and clustered population than ordinary adaptive cluster sampling.
Keywords: Adaptive Cluster Sampling with Stopping Rule (ACS’), Ordinary Adaptive Cluster Sampling (ACS), Horvitz Thompson Estimator (HT), Hansen-Hurwitz Estimator (HH), Relative Efficiency

1. Introduction
In ecology, most of the species are sparse and they tend to be found in clusters. In geology, most of the minerals are found in clusters. Thus there is a need for a good estimation design for all characteristics of interest of these minerals for commercial purpose. Adaptive cluster sampling is a sampling design that can be used to estimate the population parameters of interest for rare, clustered and endangered populations [1] . The sampling design is termed as adaptive if the sampling procedure depends on the selection rather than the assumption of the population. The basic idea behind this sampling plan is to decide on an initial sample from a defined population by some probability sampling methods such as simple random sampling and to keep on sampling within the vicinity of the units that satisfy the conditions that are defined previously. The requisites of adaptive cluster sampling design comprise of an initial selection of units, a condition that determines when additional units should be added to the sample from the neighborhood of that unit and a clear definition of the neighborhood of every unit.
There is an increase in sampling efficiency under ACS resulting in more precise estimates of the population parameter, that is, the ACS leads to an increase in the number of observation of the target species that may result in more reliable estimates of other population parameters such as species richness in information, population composition and relative abundance [2] . These advantages are more evident in rare and clustered populations [3] .
The major disadvantage of adaptive cluster sampling in estimation of population parameters is the uncertainty of the final sample size. Much attention has been focused to limit the size of the final sample in ACS [4] . However, prior knowledge of the population is required to limit the final sample [5] .
Adaptive Cluster Sampling Designs
Adaptive cluster was initiated by [1] for sampling
the population that exhibits rare and clustering characteristics. We consider a
study region divided into
 units (networks). Let
units (networks). Let
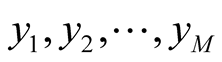 be the values of the variables observed, that is
be the values of the variables observed, that is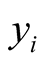 , is the number of observed
offspring or children in every network. The mean
, is the number of observed
offspring or children in every network. The mean
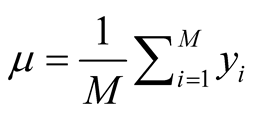 is the parameter of the observed offspring
in every unit.
is the parameter of the observed offspring
in every unit.
The adaptive design usually starts by an initial sample of unit
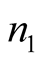 selected by some convectional design such as simple random sampling and to continue
sampling within the neighborhood of the units that satisfy the conditions that are
defined previously. The basic essentials of adaptive cluster sampling design consist
of an initial selection of units, a condition that determines when additional units
should be added to the sample from the neighborhood of that unit and a clear definition
of the neighborhood of every unit. This design was introduced by Thompson (1990)
for estimation of population parameter of rare and clustered populations. Since
the introduction of this design many researchers have had a lot of interest in the
use of this design in estimation of parameters of highly clustered and rare populations
[6] .
selected by some convectional design such as simple random sampling and to continue
sampling within the neighborhood of the units that satisfy the conditions that are
defined previously. The basic essentials of adaptive cluster sampling design consist
of an initial selection of units, a condition that determines when additional units
should be added to the sample from the neighborhood of that unit and a clear definition
of the neighborhood of every unit. This design was introduced by Thompson (1990)
for estimation of population parameter of rare and clustered populations. Since
the introduction of this design many researchers have had a lot of interest in the
use of this design in estimation of parameters of highly clustered and rare populations
[6] .
Two design-unbiased estimators were introduced by [4] based on the Horvitz-Thompson (HT) and the Hansen-Hurwitz (HH) estimators. Since the study area is divided into networks, the HT estimator uses the inclusion probability while the HH estimator uses the draw by draw probability.
Because controlling the final sample size in ACS design is a big challenge, a variant
to the original ACS design was proposed by introducing a stopping rule at each aggregative
step and for each unit in the initial sample [7]
. Once the
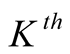 step of the aggregative procedure has been completed, further units will be sampled
if and only if
step of the aggregative procedure has been completed, further units will be sampled
if and only if
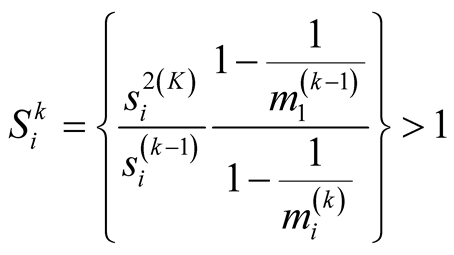 (1.1.1)
(1.1.1)
where
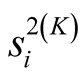 is the within-network variance estimate for the
is the within-network variance estimate for the
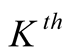 step for the
step for the
 initial unit and
initial unit and
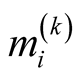 is the cardinality of the set of units adaptively sampled after the
is the cardinality of the set of units adaptively sampled after the
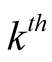 step. The condition shows how the within-network variance and the final sample size
determine the efficiency of the adaptive design.
step. The condition shows how the within-network variance and the final sample size
determine the efficiency of the adaptive design.
2. Estimators
In this section, the design based estimators will be reviewed. These estimators are design based, that is, their biasedness depends on the selection rather than the assumption of the population.
2.1. The Hansen-Hurwitz Estimator
The Hansen-Hurwitz estimator is based on draw-by-draw selection probability of selecting a primary sampling unit on any given draw. Since draw-by-draw selection probability cannot be known for all primary units in the sample but can be established for the networks, the HH estimator can be modified to use the unit that do not satisfy the condition when they are selected in the initial sample. The modified Hansen-Hurwitz estimator is expressed as
 (2.1.1)
(2.1.1)
where
![]() is the average of the
is the average of the
 values in the network
values in the network
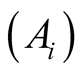 that include the
that include the
 unit of the initial sample of size
unit of the initial sample of size . If
. If
 is the number of units in the network
is the number of units in the network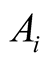 , then.
, then.
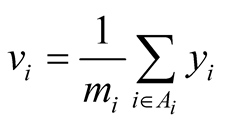 (2.1.2)
(2.1.2)
The sampling variance of the Hansen-Hurwitz estimator is expressed as
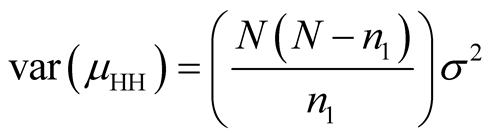 (2.1.3)
(2.1.3)
where,
 (2.1.4)
(2.1.4)
2.2. Horvitz-Thompson Estimator
The Horvitz-Thompson estimator is based on inclusion probabilities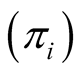 , but on application
of ACS the inclusion probabilities for every sampling unit selected in the sample
cannot be established. Nevertheless, it is possible to establish the probability
of including a network in the sample selected. A network is a subset of distinct
units within a cluster, such that selection of any unit within the network would
lead to the inclusion of all other units in the network. Units that fail to satisfy
C but are in the neighborhood of one that satisfy are referred to as edge units.
Thus, all units selected in the initial sample and fail to satisfy C will be considered
to be networks of size one. On partitioning the adaptive cluster sample into distinct
networks rather than basic sampling units, the HT estimators for the population
mean can be expressed as
, but on application
of ACS the inclusion probabilities for every sampling unit selected in the sample
cannot be established. Nevertheless, it is possible to establish the probability
of including a network in the sample selected. A network is a subset of distinct
units within a cluster, such that selection of any unit within the network would
lead to the inclusion of all other units in the network. Units that fail to satisfy
C but are in the neighborhood of one that satisfy are referred to as edge units.
Thus, all units selected in the initial sample and fail to satisfy C will be considered
to be networks of size one. On partitioning the adaptive cluster sample into distinct
networks rather than basic sampling units, the HT estimators for the population
mean can be expressed as
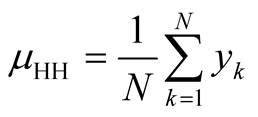 (2.2.1)
(2.2.1)
where
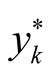 is total number of individuals in the
is total number of individuals in the
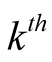 network,
network,
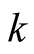 is the number of distinct networks in the
sample, and the
is the number of distinct networks in the
sample, and the
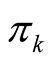 is the probability of including any unit in the network
is the probability of including any unit in the network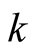 . If there are
. If there are
 units in the
units in the
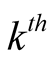 network, then the inclusion probability can be expressed as
network, then the inclusion probability can be expressed as
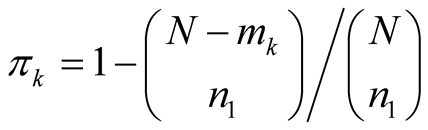 (2.2.2)
(2.2.2)
The sampling variance of the estimator is expressed as
 (2.2.3)
(2.2.3)
where
 is the probability of including both network
is the probability of including both network
 and
and
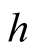 in the adaptive sample and is expressed as
in the adaptive sample and is expressed as
 (2.2.4)
(2.2.4)
3. Methods
The simulated population had a Poisson clustered population as given by [8] . In this simulation the parent was simulated on a relatively
larger area while the offspring were simulated on a smaller study area to avoid
the edge effect. The position of the offspring relative to their parents was independently
distributed. Only the offspring was retained in the final population pattern. The
study area was divided into
 units. For control of the edge effect of Poisson cluster process a
units. For control of the edge effect of Poisson cluster process a
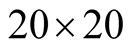 unit was selected as the study area. Each population was sampled 100 times with
SRS, ordinary ACS and ACS with data driven stopping rule.
unit was selected as the study area. Each population was sampled 100 times with
SRS, ordinary ACS and ACS with data driven stopping rule.
The efficiency of the designs was determined using relative efficiency, that is,
 , and
, and
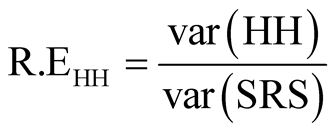 , under both the adaptive cluster sampling
designs.
, under both the adaptive cluster sampling
designs.
4. Results and Discussion
For the two populations examined for Figure 1 and Figure 2 in this study there were multiple conditions under which one or both design based estimators were relatively more efficient than the classical estimator given an equal final sample size. The Hansen-Hurwitz estimator performed uniformly worse than the Horvitz-Thompson estimator and rarely better than the SRS mean. Complete tables of the relative efficiencies of both the HT and HH estimators under all conditions are presented in Table 1 and Table2
Some interesting characteristics were observed across increasing final sample size. The efficiency of both adaptive cluster sampling estimators in ACS and ACS’ increased as the initial sample size increased. Interestingly, the HT estimators showed intense increase in efficiency with only modest increase in the sample size. For example the efficiency of the HT estimator at sampling of the population 1, that is Figure 1, from results in Table 1 increases by 0.1413 folds for ACS and by 0.0505 for ACS’ as the final sample size increases from 20 to 90. The above results are caused by the increase of the final sample size as the probability of including the large networks increases and hence resulting into low variances.
As the rarity and the clustering of the population decreases, the efficiency of design based estimators (HT and HH estimators) relative to classical estimator (SRS mean) reduces. The results of the efficiency of the HT and HH estimators from population 2 that is for Figure 1 as show in Table 2 indicate a reduction in efficiency. This indicates that the design based estimators are only efficient for population that is rare and clustered. The classical estimator perform better than the design base estimators (HT and HH estimators) for population 2 which was not rare and clustered.
Example of Fridge Oryx (A Species of Gazelle in Amboseli National Park)
The fridge-eared Oryx is a species of the gazelle. It is mostly found in the Amboseli National Park reserve in

Figure 1. The spatial point pattern for a rare population.

Figure 2. The spatial point pattern for general population.
Table 1. Relative efficiency for rare and clustered population.
Table 2. Relative efficiency for a general population that is not rare and clustered.
Kenya. The fridge-eared Oryx live in clusters that vary in different sizes. According to the Amboseli National park the species are sparsely distributed in the study of Amboseli National park. The study area was AmboseliWest Kilimanjaro/Magadi-Natorn Landscape covers portions of Southern Kenya and Northern Tanzania between 1˚37' and 3˚13' South and 35˚49' and 38˚00' East. This ecosystem comprises Amboseli and Namanga.
Magadi area in southern Kenya, and West Kilimanjaro and Natron in northern Tanzania. The survey covered approximately 24,000 km2 and extended from the foot of Chyulu hills to the east, Arusha National Park to the south, Lake Natron to the west and Lake Magadi to the north. Mt. Kilimanjaro lies to the south eastern boundary of the survey area. For purposes of this census, the survey area has been divided into four broad areas namely: Namanga-Magadi area, Amboseli area, Natron area and West Kilimanjaro area.
The number of initial sample plots was 5. Many of the initial units fell into damage class zero and no adaptive units were added from their neighborhood; however, a total of 56 units were added to the sample. The mean size of the adaptively sampled networks was 11 units of which the largest network had a total of 35 units. The HT, HH and SRS estimators for population mean and variance were calculated for the samples obtained under ACS and ACS’. The relative efficiency of the HT and HH estimators under the ACS and ACS’ designs were obtained and recorded in the Table3 With the ACS’ there is higher efficiency that the ACS estimators under the same final sample. The HT estimator has higher efficiency by approximately 0.3 than the HH estimator under the ACS’ design. Under the ACS the HT estimator report an efficiency of less than 0.4322 when the final sample is 20 to a relative efficiency of 0.1718 when the final sample is 50. The HH estimator also reports a relative efficiency of 0.7059 when the final sample is 20 to 0.3254 when the final sample is 50. This clearly indicates that the relative efficiency of the estimator under the ACS’ increases as the final sample increases. It also indicates that the HT estimator is better in estimation of the rare and clustered population.
5. Conclusions
The efficiency of the adaptive cluster sampling depends on a number of factors. According to [6] it was argued that the efficiency of an adaptive cluster sample is a function of the interaction between the within-network variance and final sample size and ultimately depends upon the spatial distribution of the target population.
This study shows that, for different populations, at appropriate sample size and any given condition for adaptive cluster sample designs, the populations can be sampled more efficiently with both ACS and ACS’. The most importance is to be able to determine what the sample size is, and the condition to adaptively add units to the sample is suitable. The results of this study also indicate that there should be no question that the HT estimator is superior to the HH estimator for use in both ACS and ACS’ settings. Although the HH estimator uses the adaptively added units to adjust the values of the initially sampled units to network means, it does not explicitly incorporate any of these additional unit values directly into the estimate.
The choice of condition C is very important. A highly restrictive condition will result in lower final sample sizes and less empty edge units being sampled, but for some populations it may result in little additional information being added to the sample and the full benefit of an adaptive cluster design may be lost. However, for populations that seem not to exhibit the appropriate level of geographical rarity for the practical implementation of ACS, the choice of a restrictive condition can result in geographically rare networks that will add information and precision to the sample without the danger of an exorbitant final sample size. This study showed that even the smallest change in the condition to adaptively add units to the sample can have strong effects on both the efficiency of ACS and the final size of the sample. A less restrictive condition results in sampling of higher proportion of population, but results in final sample size that is much higher and costly to implement. Hence, the choice of the condition C must be made in reference to sampling time, and cost of implementing the study.
References
- Dryver, A.L. and Chao, C.T. (2007) Ratio Estimators in Adaptive Cluster Sampling. Environmetrics, 18, 607-620. http://dx.doi.org/10.1002/env.838
- Turki, P. and Barkowski, J.J. (2005) A Review of Adaptive Cluster Sampling: 1990-2003. Environmental and Ecological Statistics, 12, 55-94. http://dx.doi.org/10.1007/s10651-005-6818-0
- Thompson, S.K. (1990) Adaptive Cluster Sampling. Journal of American Statistical Association, 85, 1054-1059.http://dx.doi.org/10.1080/01621459.1990.10474975
- Noon, B.R., Ishwar, N.M. and Vasudevan, K. (2006) Efficiency of Adaptive Cluster and Random Sampling in Detecting Terrestrial Herpetofauna in a Tropical Rainforest. Wildlife Society Bulletin, 34, 59-68.http://dx.doi.org/10.2193/0091-7648(2006)34[59:EOACAR]2.0.CO;2
- Philippi, T. (2005) Adaptive Cluster Sampling for Estimation of Abundances within Local Populations of Low Abundance Plants. Ecology, 86, 1091-1100. http://dx.doi.org/10.1890/04-0621
- Kenya Wildlife Service (2010) Aerial Total Count: Amboseli-West Kilimanjaro/Magadi-Natron Cross Border Land Scape.http://www.kws.org/export/sites/kws/info/publications/census_reports/Amboseli_West_kili_Magadi_Natron_2010_cesus_report.pdf
- Smith, D.R., Brown, J.A. and Lo, N.C.H. (2004) Application of Adaptive Cluster Sampling to Biological Populations. In: Thompson, W.L., Ed., Sampling Rare or Elusive Species, Island Press, Covelo, 93-152.
- Diggle, D.J. (1983) Statistical Analysis of Spatial Point Patterns. Academic Press, London.
NOTES

*Corresponding author.


