Open Journal of Statistics
Vol.04 No.04(2014), Article ID:47088,4 pages
10.4236/ojs.2014.44031
Statistical Diagnosis for Random Right Censored Data Based on Kaplan-Meier Product Limit Estimate
Shuling Wang1, Xiaohong Deng1, Lin Zheng2
1Department of Fundamental Course, Air Force Logistics College, Xuzhou, China
2School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu, China
Email: 155328313@qq.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2014; revised 15 May 2014; accepted 2 June 2014
ABSTRACT
In this work, we consider statistical diagnostic for random right censored data based on K-M product limit estimator. Under the definition of K-M product limit estimator, we obtain that the relation formula between estimators. Similar to complete data, we define likelihood displacement and likelihood ratio statistic. Through a real data application, we show that our proposed proce- dure is validity.
Keywords:
Random Right Censorship, Kaplan-Meier product-limit Estimator, Empirical Likelihood, Outliers, Influence Analysis

1. Introduction
Statistical diagnosis developed in the mid-1970s, which is a new statistical branch.
In the course of development of the past 40 years, most scholars have studied the data into a convenient and effective statistical model. For example, the diagnosis and influence analysis of linear regression model has been fully developed (R. D. Cook and S. Weisberg [1] , Bocheng Wei, Guobin Lu & Jianqing Shi [2] ); The varing coefficient model is a useful extension of classical linear model. Regarding the varying coefficient model, espe- cially for the B-spline estimation of parameter, diagnosis and influence analysis have some results (Cai, Z., Fan, J., Li, R. [3] , Fan, J., Zhang, W. [4] ). However, all the above results are obtained under the uncensored case. In many applications, some of the responses and/or covariants may not be observed, but are censored. For censored data, the usual statistical techniques for complete data situations are not readily applicable. Because there are too many hypothesis, it is easy to lose information.
As we all known, the distribution function of a random variable X contains all of the probabilistic information about X. Hence this paper tries to use non-parametric maximum likelihood estimate (NPMLE) [5] of distribu- tion function in follow-up study.
The rest of the paper is organized as follows. The right censoring and K-M product limit estimator is intro- duced in Section 2. Outlier diagnosis and influence analysis are presented in section 3. An example is given to illustrate our results in Section 4.
2. Right Censoring and Kaplan-Meier Product Limit Estimator
Here, the distribution of a real-valued random variables 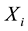 is of direct interest. For each
is of direct interest. For each  there is a
there is a
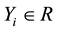 . This
. This 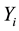 may be random. If
may be random. If  we observe
we observe , otherwise
, otherwise 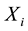 is censored to
is censored to . We say
. We say
that 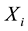 is right censored by
is right censored by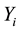 . Let
. Let 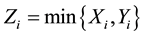 and
and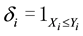 . For example,
. For example, 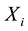 could be survival
could be survival
time after an operation, with 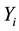 the time from the operation to the end of the study.
the time from the operation to the end of the study.
The idea of the K-M product limit estimator is given by the conditional probability. Let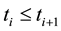 :
:
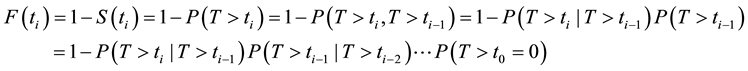
We assume that at the start of the study all subjects were alive, so
bility is

where 




3. Statistical Diagnostic
For complete data, diagnostic measures of outlier contain case deletion and mean shift, influence statistics con- tain Cook’s distance, W-K statistic, covariance ratio statistic, AP statistic, likelihood distance and so on. Simi- larly, we derive several diagnostic measures for right censored data.
3.1. Outlier Diagnosis
Let 

Proof: By the definition of K-M product limit estimator, there are
and
Since, when
when

From the lemma, we can construct the relation formula between estimators, which is the foundation of discus- sion.
3.2. Influence Analysis
3.2.1. Likelihood Displacement
The likelihood function is defined as
where


from uncensored
Likelihood displacement is the method for measuring influence, which is advanced by Cook and Weisberg in 1982, which is advanced from the view of data fitting. Considering the influence of deleting the 

3.2.2. Likelihood Ratio Statistic
For complete data, there is likelihood ratio statistic. Similarly, we define the likelihood ratio statistic for cen- sored data based on K-M product limit estimator as follows
4. Numerical Studies
(Vicious Tumour Data) In this section, we consider an example as the illustration for the above results. Consi- dering a clinical research trial data (see Andersen [6] ). There are 205 cancer patients who have been treated in Odense university hospital and tracked until the end of 1977. The survival time of some individuals due to death or end of the trial for other reasons were censored. Wang Qihua [7] ultized a linear semi-parametric model to fit these test data. Wang Shuling et al. [8] ultized a nonparametric regression model with random right censorship to fit the data of 126 female patients. Now we consider the first twenty data, calculate the likelihood function
by MATLAB and obtain
where 



lows.
Table 1. The originality data and the value of
Figure 1. The value of LDi.
Figure 2. the value of Ri.
Figure 1 and Figure 2 show that the first, second, third, fourth and fifth data are outliers. Indeed, this result is similar to Wang Shuling et al. [8] .
References
- Cook, R.D. and Weisberg, S. (1982) Residuals and Influence in Regression. Chapman and Hall, New York.
- Wei, B.C., Lu, G.B. and Shi, J.Q. (1990) Statistical Diagnostics. Publishing House of Southeast University, Nanjing.
- Cai, Z., Fan, J. and Li, R. (2000) Efficient Estimation and Inferences for Varying-Coefficient Models. Journal of American Statistical Association, 95, 888-902. http://dx.doi.org/10.1080/01621459.2000.10474280
- Fan, J. and Zhang, W. (2008) Statistical Methods with Varying Coefficient Models. Statistics and Its Interface, 1, 179-195. http://dx.doi.org/10.4310/SII.2008.v1.n1.a15
- Owen, A. (2001) Empirical Likelihood. Chapman and Hall, New York. http://dx.doi.org/10.1201/9781420036152
- Andersen, P.K., Borgan, O., Gill, R.D. and Keiding, N. (1993) Statistical Models Based on Counting Processes. Springer-Verlag, New York.
- Wang, Q.H. (2006) Analysis of Survival Data. Science Press, Beijing.
- Wang, S.L., Feng, Y. and Liu, X.B. (2010) Statistical Diagnostics of Nonparametric Regression Model with Random Right Censorship. Journal of Hefei University of Technology (Natural Science), 33, 470-473.










